基于多源数据的房地产价格指数预测模型及实证研究

朴春慧， 武旭晨，2， 蒋学红， 李玉红

（1.石家庄铁道大学 信息科学与技术学院，河北 石家庄 050043；2.中国银行河北省分行 信息科技部，河北 石家庄 050000；3.河北省住房和城乡建设厅 信息中心，河北 石家庄 050051；4.石家庄铁道大学 经济管理学院，河北 石家庄 050043）

一个国家或地区的经济发展与房地产业的运行状况息息相关。但当前与房地产价格相关的理论研究不成熟，评估方法较为依赖对过去的经验，一定程度上影响了房地产评估行业的发展[1]。当前对房地产价格的预测存在着几点不足。第一，由于我国房地产市场起步较晚，数据不完整，现有研究大都以年度数据对模型进行实证研究，数据量不够充足，影响了模型的准确率[2]；第二，以往的研究表明，民众对于房地产市场的预计期望是决定房地产市场价格的重要因素[3]，而现有的价格预测中少有考虑民众预期这一指标；第三，现有研究大多使用房价作为房地产市场热度的度量指标，但是由于房地产开发周期较长，加之土地供给量对其价格的约束较大，且与银行信贷关系密切，因此用房价作为整个房地产市场的度量指标有一定的局限性[4]。

住宅销售价格指数是综合反映住宅商品价格水平总体变化趋势和变化幅度的相对数。它通过百分数的形式来反应房价在不同时期的涨跌幅度。其优点是同质可比，这种方法反映的是排除房屋质量、建筑结构、地理位置、销售结构因素影响之后，由供求关系及成本波动等因素带来的价格波动。北京市统计局给出了房价指数的具体计算说明[5]，具体操作是在住宅价格的基础上，依据同质可比的原则，按月调查每处住宅的价格变动，对其涨跌幅度进行加权平均，最终得到全市住宅价格的变动幅度。假设某市3、4月份住宅交易情况如表1所示， 房价指数编制原理可以简化为以下计算过程：

表1 某市3、4月份住宅交易情况

按交易面积加权计算的环比价格指数为：

按交易金额加权计算的环比价格指数为：

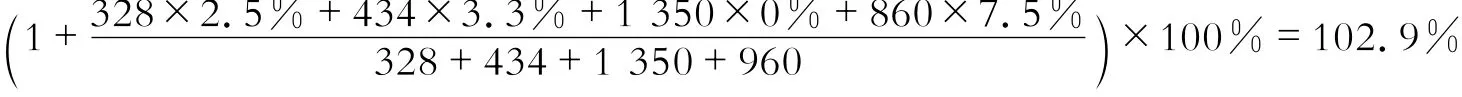
当月价格环比指数为上述环比指数的算术平均数103.5%。由此可知，房价指数剔除了住宅之间的品质差异，能够更加准确反映全市住宅价格的总体变化程度[5]。

住宅销售价格指数分为城镇新建住宅销售价格指数和二手住宅销售价格指数两部分。其中，城镇新建住宅销售价格指数的统计范围是所有进入房地产市场第一次进行产权交易及网上签约的住宅交易价格，分为保障性住房和新建商品住宅两部分[5]。本文主要研究的是影响因素对于新建商品住宅的非线性映射关系，从而预测其发展趋势，因此本文将国家统计局公布的新建商品房住宅销售价格指数作为房地产价格的度量指标。

针对房地产价格与其影响因素之间复杂的非线性关系，本文使用了两种常用的机器学习算法来预测房地产价格的发展趋势，旨在有效降低由于评估人员主观因素所造成的评估结果的偏差。在实证研究中参照住房和城乡建设部门的政务数据，收集整合了房产市场供求数据、宏观经济调控政策、人们对当前房价的预期和当前本市房产经济发展情况等多源异构数据，建立了两种房地产价格预测模型，并以华北某城市的月度数据为基础，结合ARIMA模型和经典BP神经网络模型对两种房地产价格评估模型进行了对比分析。

一、房地产价格评估指标体系

房地产市场与社会经济联系密切，同时受国家经济政策和预期计划影响，也与民众对当前房地产价格的预期紧密相关[3]。莫连光[6]使用经济、行政、区域等因素来估算房地产市场价格；王筱欣[7]使用供给因素、需求因素以及经济发展因素对重庆市房价进行了验证与预测。刘佼[1]以成都市为例引入了国民经济和房地产内部协调等指标组成了房地产市场警兆指标体系。本文在全面参考房地产价格评估研究成果和数据挖掘模型性能的基础之上，结合实验数据结构，参照政府部门数据，选定了一种房地产价格评估指标体系。以房地产供求关系、社会宏观经济指标、国家货币政策、民众对房价的预期和房地产价格现状作为一级指标，共17项二级指标组成房地产价格评估指标体系（表2）。为保证预测模型的超前性，本文使用上一个月的指标数据来预测当前月的房地产价格指数。

表2 房地产价格评估指标体系

表2中，市商品房销售成交面积/商品房批准预售面积（月）、月新开工面积增长率（%）、月实际成交面积增长率（%）、住宅实际成交面积/商品房实际成交面积（月）、商品房均价（元）来自住房和城乡建设部门信息中心大数据分析平台；市固定资产投资_累计增长（%）来自市统计局大数据平台；二手住宅销售价格指数（上年=100）、城市居民消费价格指数（上年同期=100）（%）、新建商品住宅销售价格指数（上年=100）来自国家统计局；市月度GDP是影响房地产价格的重要影响因素，但当前发布的GDP为季度数据，月度数据缺失，但市规模以上工业增加值_累计值（亿元）月度数据与市月度累计GDP关联度较大，是GDP统计中的重要参考，本文使用市规模以上工业增加值_累计值（亿元）近似表示当月GDP；存款基准利率（调整后）（%）、贷款基准利率（调整后）（%）、大型金融机构存款准备金率（调整后）（%）、中小型金融机构存款准备金率（调整后）（%）、货币供应量（亿元）、货币供应量同比增长来自中国人民银行官方网站；上阶段预期本阶段房价上涨的人数占比（%）来自中国人民银行储户问卷调查报告。

二、BP-Adaboost算法

BP神经网络（Back Propagation Neural Network）是一种使用误差逆向传播算法训练得到的多层前馈型神经网络。其对应算法为BP算法（误差反向传播算法），是一种经典的监督学习算法，其优化目标是使所有样本经过计算后的输出结果与目标输出之间的均方误差最小。算法主要分为两个阶段：信息前馈传递阶段和误差反向传播阶段[8-9]。在信息前馈传递阶段，每层的输入信息首先通过连接权值进行计算，通过相应的激活函数进行变换得到输出信号，再将输出信号作为输入传入下一层继续进行信息变换，最终得到网络输出；在误差反向传播阶段，计算神经网络的输出与真实标签间的误差，通过连接权值从输出层反向传播至输入层，最后依据梯度值更新连接权值。信息前馈传递阶段和误差反向传播阶段构成了一个迭代过程，循环不断地更新神经网络中的权值和阈值，达到预先设置的迭代终止条件后结束，最终实现神经网络中权值和阈值的最优。

Boosting方法是一种用来提高弱分类算法准确度的算法，基本思想是不断使用基础分类模型对数据进行分析建模，在建模过程中通过不断改变错分样品的权重，建立一系列基础分类模型，最后对其进行线性加权组合得到一个强分类器[10]。1995年，FreundandSchapire提出的Adaboost算法是Boosting算法的一个典型代表[11]。其主要流程为：首先给出弱学习算法和样本空间（x，y），从样本空间中找出n组训练数据，每组训练数据的权重都为1/n。然后用弱学习算法迭代运算K次，每次运算后按照分类结果更新训练数据的权重分布，对于分类失败的训练个体赋予较大权重，下一次迭代运算时更加关注这些训练个体。弱学习算法通过反复迭代得到一个分类函数序列f1，f2，… ，fK，每个分类函数赋予一个权重，分类结果越好的函数，其对应权重越大。K次迭代之后，由弱分类函数加权得到最终的强分类函数F[12-13]。

本文使用BP-Adaboost预测器作为房地产价格指数的预测模型之一。BP-Adaboost预测器是以BP神经网络作为模型的弱预测器，通过Adaboost算法得到的由多个BP神经网络组成的一种强预测器。

三、支持向量回归算法

支持向量机 （SupportVectorMachine，SVM）[14-15]是在统计学习理论的VC维理论和结构风险最小原理的基础上发展起来的一种机器学习方法。支持向量回归是支持向量机在回归问题上的扩展，Vapnik在ε不敏感损失函数的基础上提出了ε支持向量回归机（ε-SVR），它要解决一个原始优化问题：

对于非线性回归问题，引入变换φ，将样本映射到高维空间，再引入Lagrange函数，将凸二次规划问题转化为下面的对偶问题[16]：

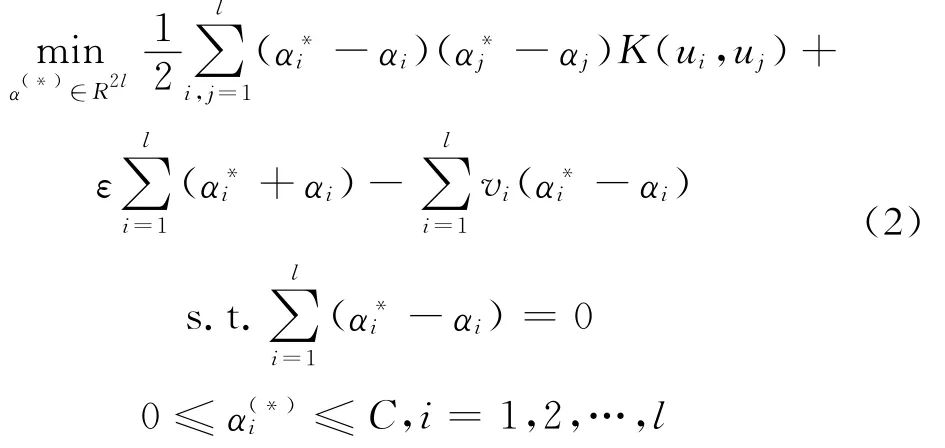
回归估计模型转化为：

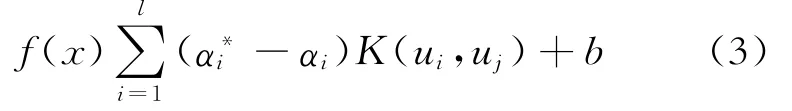
式中，K（ui，uj）为核函数；C为惩罚参数；α（*）=为Langrangec乘子向量，αi和为向量中的元素。

本文以支持向量回归机作为房地产市场价格指数预测的模型之一，通过之后的调参工作确定相对参数，使得模型的预测性能最优。

四、实证研究

（一）样本数据的收集与处理

本文以华北某市的房地产市场为示例对象，验证房地产价格指数预测模型的优劣。本文收集了2010年1月开始至2017年6月关于此市的各类月度指标数据90条（如表3所示）。数据集中，固定资产投资、规模以上工业增加值缺失一月份数据，由于其值为累计数据，本文使用每月的平均增长值得到其一月份的估计值。预期下季房价上涨的人数占比指标数据频率较低，需要将低频数据转换为高频月度数据，本文假设当前月度的房价预期与当前季的预期数据相同。

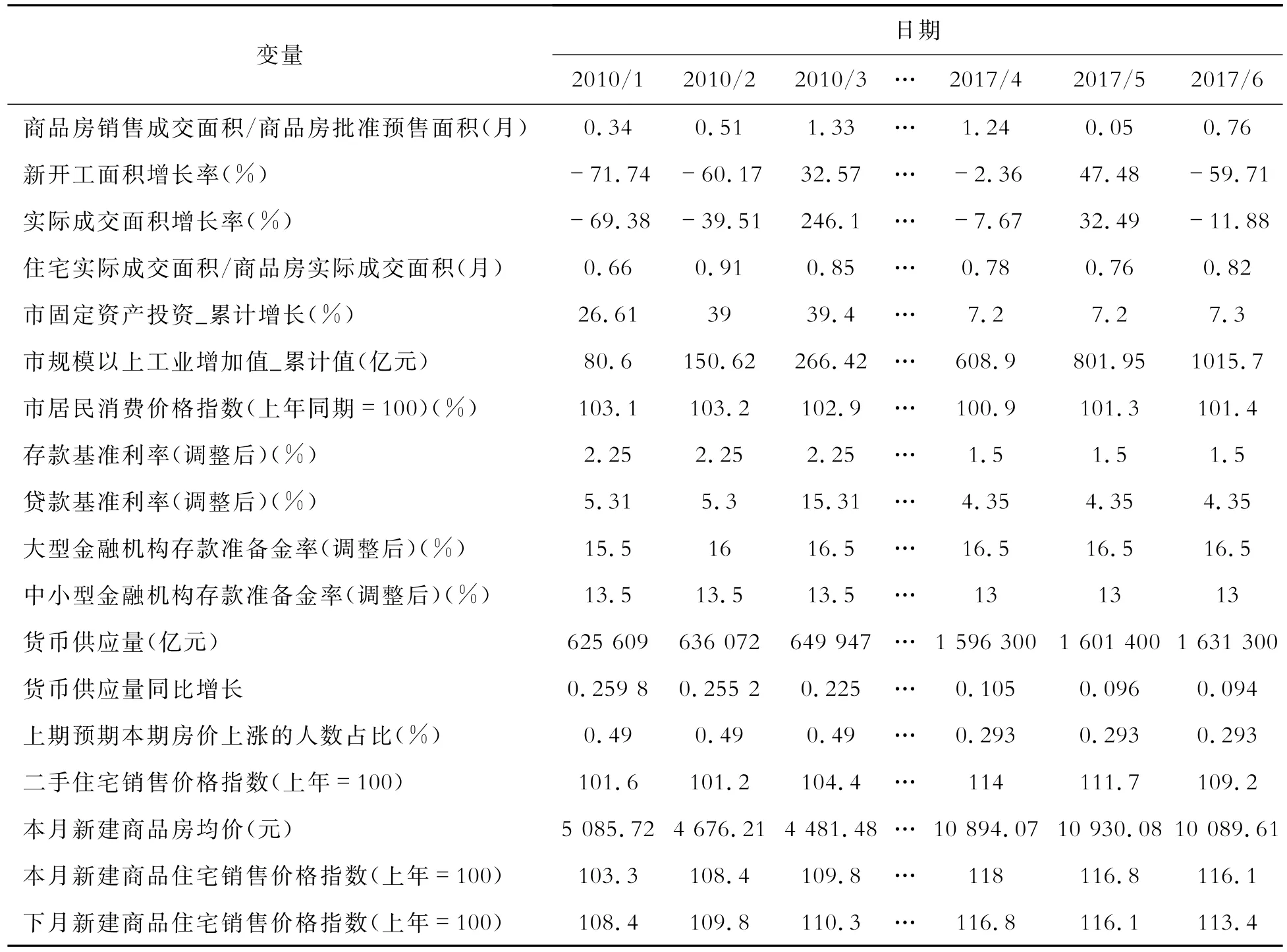
表3 华北某市房地产市场评估指标数据

由于各影响因素指标的表现形式不同，个别输入分量差距较大，不能体现各分量的同等地位。且输入过大时，网络容易进入S型函数的包河区，导致网络无法收敛[12]。因此在网络计算之前需要对样本数据进行标准化处理，以提高网络的训练速度。结合样本数据的特点及量化标准与房地产价格成正比的特性，本文采用了归一化的标准化方法。

为了准确比较两种预测模型的预测性能，本文按照8∶1的比例将数据集随机地划分成训练集和测试集，使用训练集分别训练两种预测模型，使用测试集验证模型的预测性能。为了排除随机划分数据集可能造成的偶然性结果，本文将上述实验进行了6次，以6次实验的均值作为判断模型预测性能的数据依据。

（二）BP-Adaboost模型的建立

BP-Adaboost算法的参数主要分为强预测器Adaboost的训练误差、训练次数，和弱预测器BP神经网络中训练误差、隐含层数、节点个数和传递函数与训练函数。Adaboost中训练误差的设置不可太小，否则容易出现过拟合，也不能太大，容易出现欠拟合。本文借助MatlabR2016a中的神经网络工具箱，建立了BP-Adaboost预测模型。

经过多次重复实验后，本文设置Adaboost的训练误差为2，训练次数为20。使用3层BP神经网络作为弱预测器，根据训练样本设置输入层节点数14个，输出层1个。根据Hornik公式，隐层节点]（其中，n为输入层节点个数，m为输出层节点个数），设置隐含层节点数为20。设定弱预测器BP神经网络的误差精度为0.0001，隐含层传递函数采用正切Sigmoid函数tansig（），输出层传递函数采用S型激发函数logsig（），网络训练函数采用tringlm（），设置最大训练次数为1000次，学习率为0.1，目标误差为0.0001。

Adaboost组合预测模型具体建模步骤如下：

（1）样本数据权重初始化。首次迭代时设置每个样本数据的权重相等，为D1（k）=1/n（k=1，2，…，n）。

（2）弱预测器预测。每次迭代前将当前的BP网络权值初始化为0，通过训练集训练n个弱预测器。若某一样本数据预测误差大于设定的阈值，表示产生了较大误差，则将其累计权值相加得到这一弱预测器的权值之和：

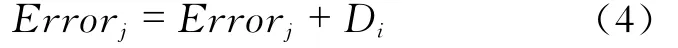
式中，Errorj代表第j个弱预测器权值累加和；Di代表超过误差阈值的数据的权值。

（3）更新样本数据权重。若当前BP网络的预测结果对此样本误差较小，未超过阈值，则其权值Di不变。若超过误差阈值，则权值相对增加：

（4）弱预测器权值计算。根据弱预测器权值累加和Errorj计算当前BP网络的权值：

（5）构建强预测器。经过n次迭代后得到强预测器：

（三）支持向量回归模型的建立

本文借助Python中的Scikit-Learn模块建立了基于支持向量回归算法的价格指数预测模型。Scikit-Learn模块使用了SVR和NuSVR两种回归方式，相对于传统SVR，NuSVR增加了一个参数nu来控制支持向量的百分比，在使用时与SVR中的参数ε等价。为获得最优的预测效果，本文比较了两种回归方式的优劣，选择性能最佳的回归方式作为最优预测模型。

核函数是支持向量机的核心，核函数的选择直接影响支持向量归回模型的准确度。本文对常用的Linear核函数、径向基核函数、Sigmoid核函数和Poly核函数做了对比分析。结合两种回归算法，共需要28个参数进行优化。具体需要优化的参数如表4所示。

表4中，需要优化的参数用√表示。核函数参数degree对应多项式核函数中的参数d；参数gamma分别对应多项式核函数、高斯核函数和sigmoid核函数中的参数γ；参数coef0分别对应多项式核函数和sigmoid核函数中的参数r。

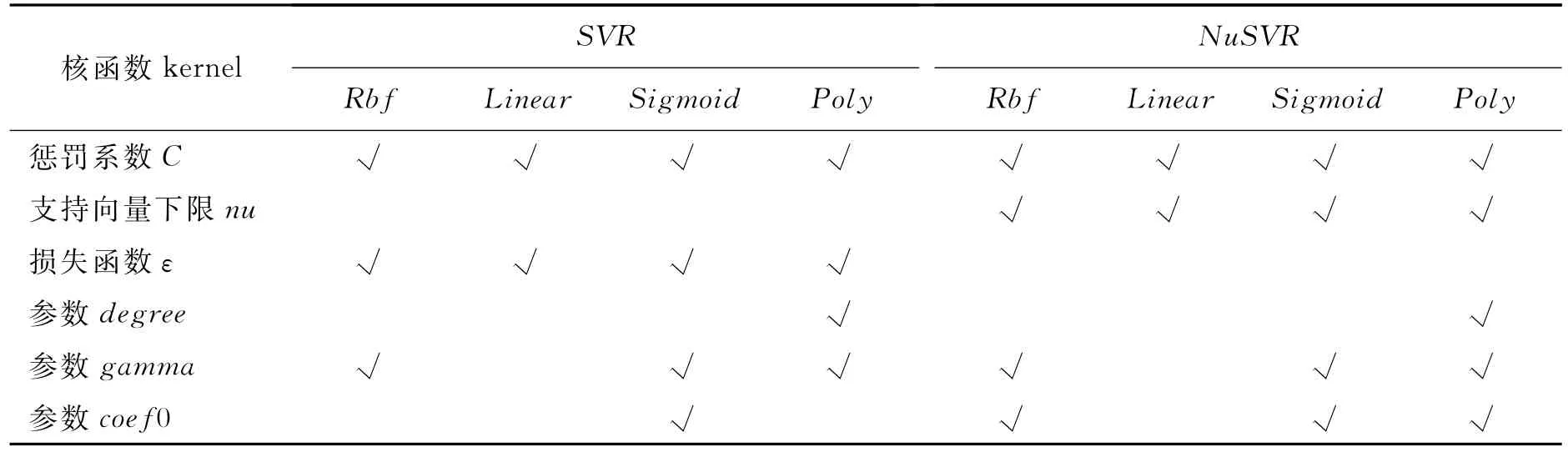
表4 不同核函数中需要优化的参数

由于支持向量回归模型的参数较多，手工调参工作量较大。为简化调参工作，本文设计了一个调参算法对回归模型进行参数优化。由于本文提出的指标体系为时间序列数据，部分指标数据在一段时间内没有改变（如贷款利率），所以在训练集和测试集的划分时需要考虑这种数据对模型的影响。我们将全部数据随机地划分了50次，其中以80条数据作为训练集，10条数据为测试集对模型进行调参工作。以模型在50次不同划分方式下对测试集的拟合优度作为回归模型性能优劣的评判标准。算法流程如图1所示。

图1 支持向量回归机参数优化流程图

本文使用决定系数R2对模型的拟合优度进行评价[17]，R2越接近于1表示模型对数据集的拟合优度越好，其表达式为

图2给出了NuSVR-Rbf模型的参数优化结果，黄色实线表示模型对训练集的拟合优度及其方差，蓝色虚线表示对测试集的拟合优度及其方差。根据图2中显示，参数C的最优值在3.0附近。图3给出了不同回归方式下8种模型的性能优劣。其中，图3（a）表示模型对测试集的拟合优度，图3（b）表示模型对训练集的拟合优度，点为均值，线为方差。实验结果显示，NuSVR-Rbf模型的性能最优，可作为支持向量回归的最优预测模型。

图2 NuSVR-Rbf中参数C的优化示意图

图3 8种模型预测性能比较

（四）实验结果及模型比较

为准确判断两种预测模型的预测性能，本文使用ARIMA模型和经典BP神经网络与本文模型做对比。由于ARIMA模型具有不直接考虑其他相关随机变量变化的特点，对未知时间的预测只与时间序列有关，且只能预测未来连续一段时间内价格指数的趋势，而经典BP神经网络与本文所提出的支持向量回归模型和BP_Adaboost模型可随机预测不同时间的价格指数。为了排除实验过程中随机划分数据集可能造成的偶然性结果，本文按8∶1的比例将90个月的数据划分为训练集和测试集，并重复划分了6次，从而得到不同的数据集6组（Dataset1～Dataset6），以判断经典BP神经网络与本文所提模型的预测性能。为判断连续型时间序列作为训练集所得的模型对未来较长时间段的预测精度，本文以数据集中前80个月的数据为训练集，后10个月的数据为测试集组成数据集Dateset7，以判断ARIMA模型和经典BP神经网络模型与本文所提模型在连续型时间序列条件下预测性能的优劣。表5～表7分别展示了6组数据集下支持向量回归模型、BP-Adaboost模型和BP神经网络的实验结果，表8展示了连续型时间序列下4种模型的实验结果。

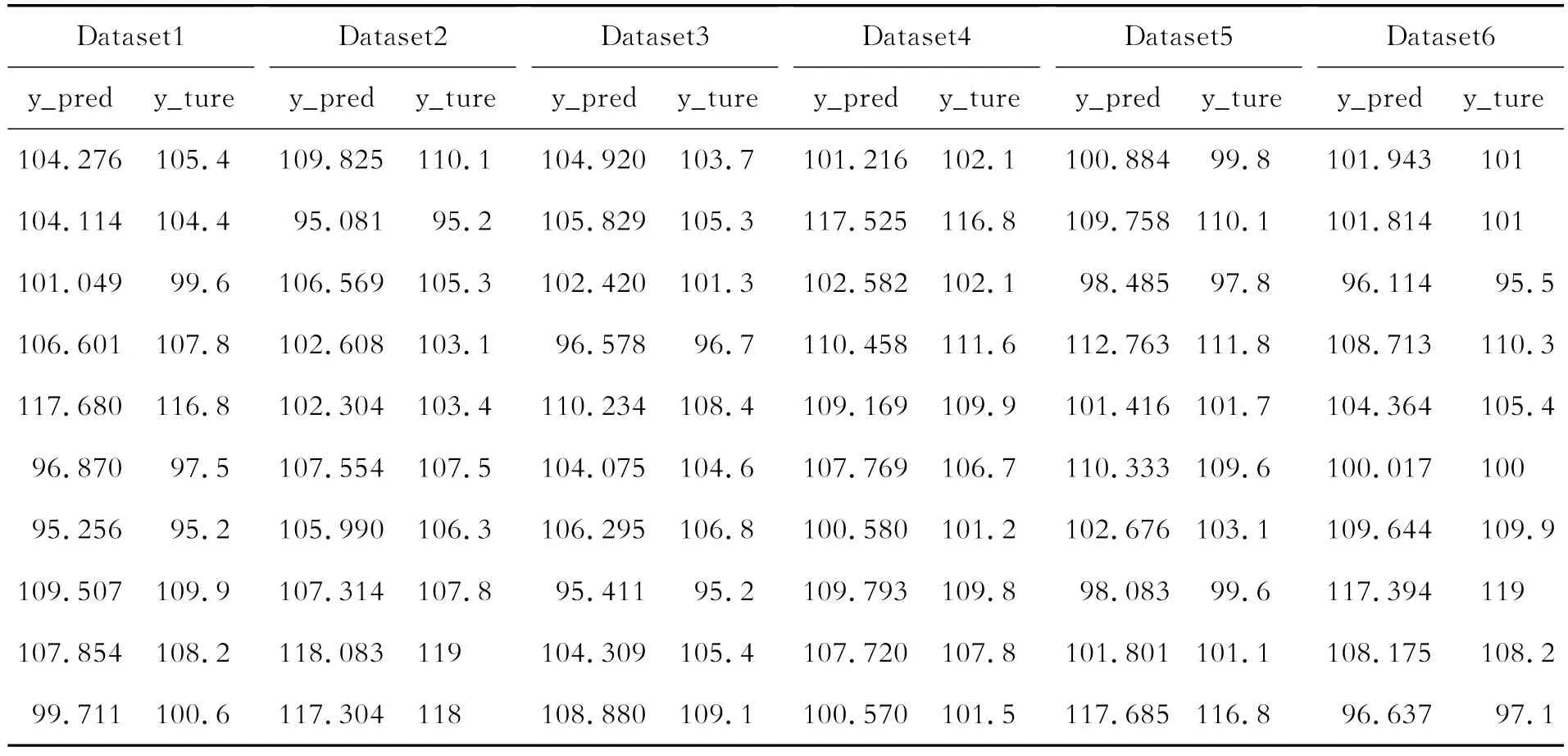
表5 支持向量回归模型实验结果

Dataset 1Dataset 2Dataset 3Dataset 4Dataset 5Dataset 6 y_predy_ture 104.380105.4110.305110.1104.982103.7101.345102.199.78499.8101.ture y_predy_ture y_predy_ture y_predy_ture y_predy_ture y_predy_841101 103.913104.4 95.69495.2105.580105.3116.789116.8110.262110.1100.787101 100.57899.6106.592105.3102.687101.3102.586102.198.87597.8 95.293 95.5 107.115107.8102.496103.1 96.51496.7110.018111.6111.436111.8110.718110.3 117.381116.8102.748103.4108.256108.4109.389109.9102.136101.7104.847105.4 97.18097.5106.767107.5103.594104.6106.612106.7110.365109.6 99.581100 95.84095.2106.604106.3106.156106.8 99.984101.2102.687103.1110.700109.9 109.362109.9107.292107.8 95.58895.2110.768109.898.88599.6117.391119 107.180108.2120.026119 104.161105.4107.471107.8100.786101.1107.743108.2 100.186100.6117.298118 108.754109.1101.719101.5117.587116.8 96.784 97.1

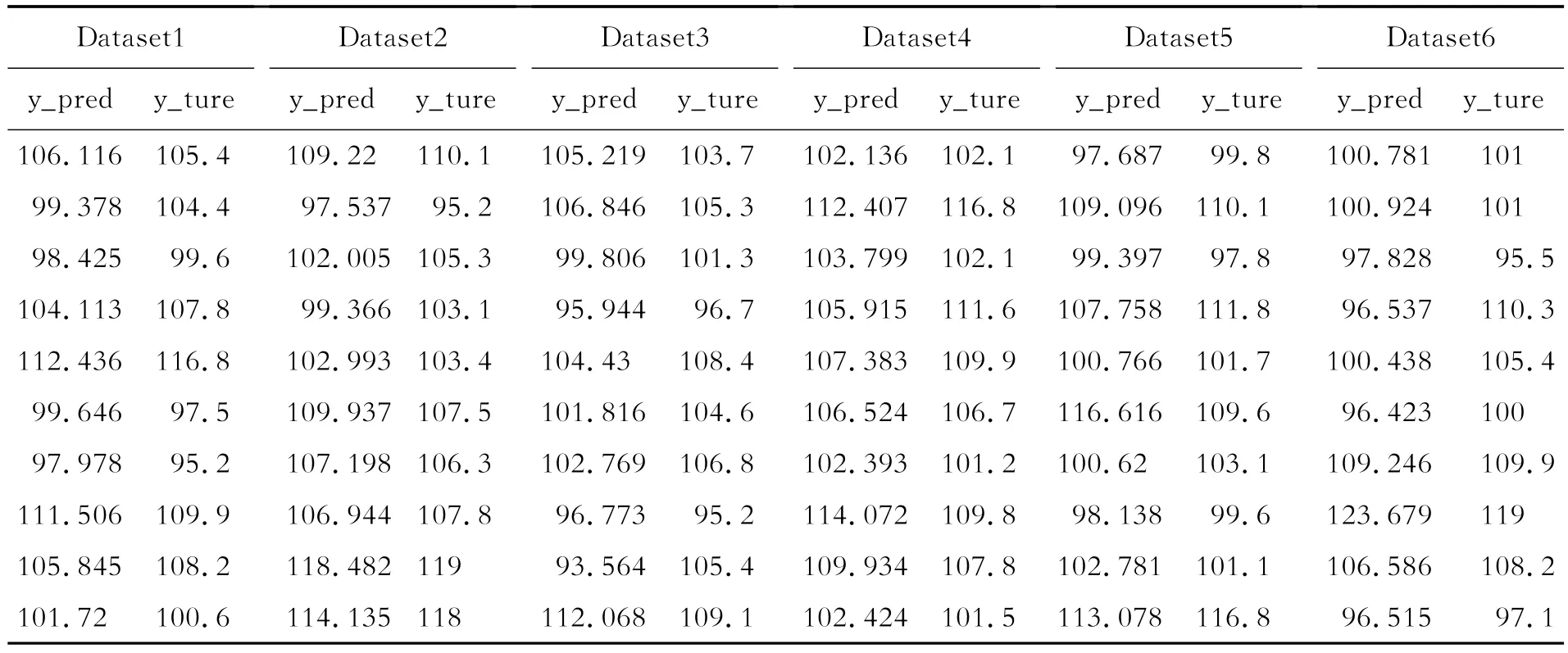
表7 BP神经网络模型实验结果

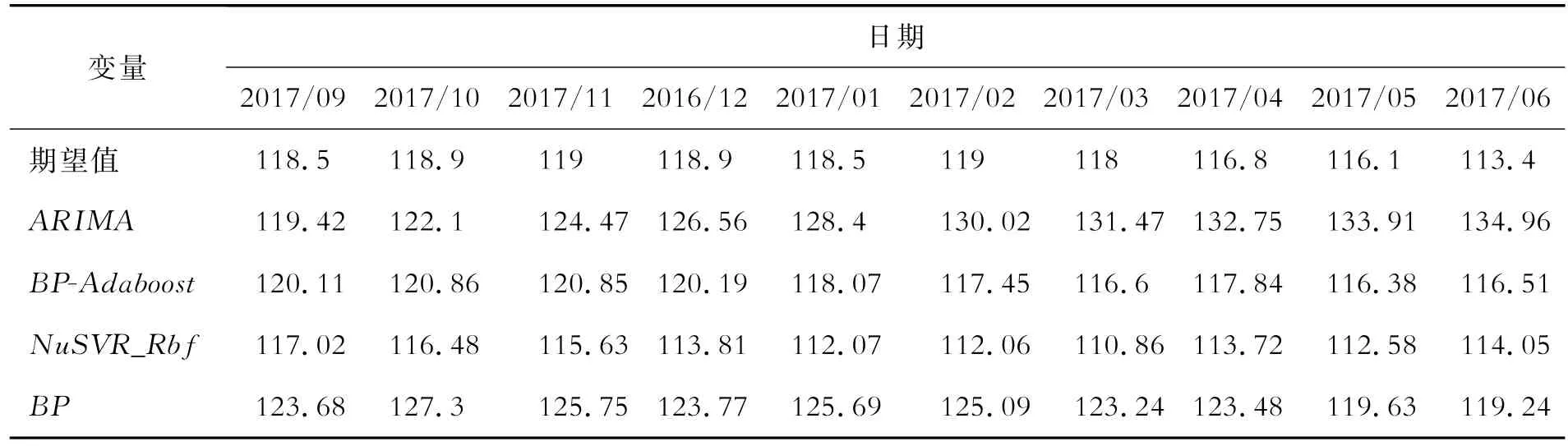
表8 连续时间序列下四种模型的实验结果

考虑到房地产价格指数是一个反映价格变化趋势和变化幅度的相对数，本文使用平均绝对误差MAE[18]对模型性能进行评价，如式（9）所示。模型在6个随机数据集下的预测精度如表9所示。

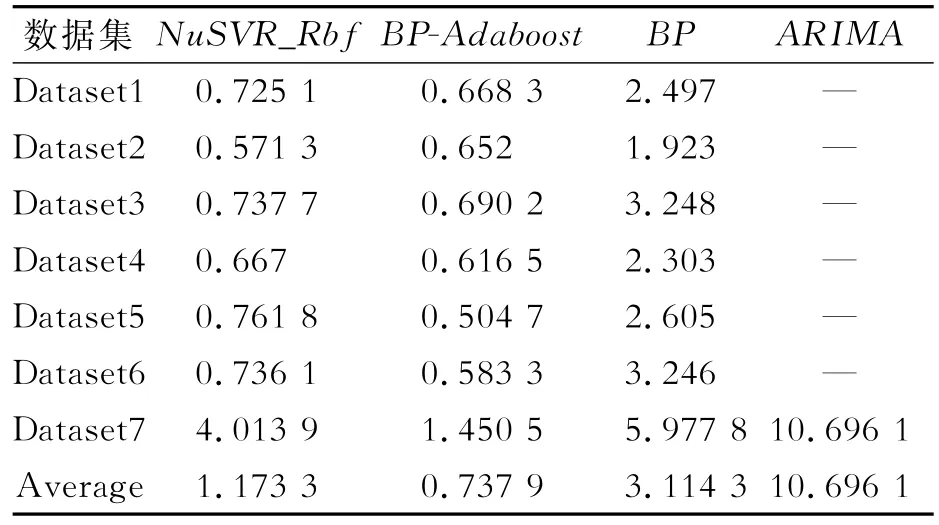
表9 四种模型的平均绝对误差

由表9可知，使用随机划分的数据集训练得到的预测模型，其平均绝对误差均比使用连续时间序列数据集训练得到的预测模型小。在所有数据集中，BP-Adaboost模型对测试集数据预测的平均绝对误差最小。

五、结束语

考虑到房地产市场与其影响因素的非线性映射关系，本文结合房地产供求关系、社会宏观经济指标、国家货币政策、民众对房价的预期和上月房地产价格现状等多源异构数据提出了一套房地产价格评估指标体系。分别使用BP-Adaboost算法和支持向量回归算法建立了两个房地产价格指数预测模型，以华北某市为对象对预测模型做了示例研究，并与ARIMA模型和经典BP神经网络模型作对比。实验结果表明，使用随机划分的数据集训练得到的预测模型比使用连续时间序列数据集训练得到的预测模型误差小。推测可能是由于预测时间段内房地产市场出现了变化，过去的预测模型不再适用。同时，相较于其他三种模型，BP-Adaboost模型的预测误差最小，使用BPAdaboost模型预测房地产价格指数具有可行性。