基于Dip-dist算法的区域合并图像分割*

张 亭 陈 柳 王嘉伟 文笃石

（西安邮电大学计算机学院 西安 710121）

1 引言

图像分割是一项比较重要的图像处理技术，其是模式识别、计算机视觉、图像处理领域中的基础和关键，在图像处理领域占有举足轻重的地位［1～2］。图像分割的质量直接影响到图像分析与理解的效果［3］。图像分割就是将目标图像划分成若干个特定的具有独特性质的区域或模块，并使这些特征在同一区域内呈现相似性，而在不同区域间呈现出明显的差异性，并且从这些区域中提取出有价值的或者感兴趣内容的技术与过程，基于此才可以进一步对它们进行理解以及对图像进行分析［4～5］。图像分割的最终目的是对图像中不同区域的目标对象进行检测、特征提取以及分类识别。图像分割是图像处理技术领域中一个至关重要的技术［6～9］，因为它是作为图像处理的前期步骤，分割的好坏直接影响到后续处理过程的结果，如特征提取，目标识别等。在实际应用中，图像分割再众多领域中起到了关键的作用，随着人们对图像分割技术越来越深入的研究，图像分割技术已经广泛应用于各个领域，如通信、军事、遥感图像分析、医学诊断治疗、智能交通、农业现代化以及工业自动化等。同样，在学术研究领域中，图像分割也是一项比较前沿而且具有重大意义的研究课题，图像分割技术的研究在很大程度上推进了人工智能，机器学习等学科的发展与成熟。

Dip-test算法是Dip-dist算法的前身，由Engelman和Hartigan（1969）［10］提出的相关测试将样本分为两个子集，最大化两个子集，采用不同方法从法线采样似然比，而零假设的均值相等。测试统计量最大的所有部门的似然比。该分布是渐近正态的（Hartigan，1978）［11］，统计量很容易计算，但当双峰替代方案不是正常混合时，测试将无法正常进行。

J.B.Kruskal（1971）［12］等提出了基于连续顺序统计间隔的测试，但该测试要求事先规定两种模式。基于间隔的另一种测试使用双峰分布，有一个很大的间隔伴随着任何一方的许多小间隔，在Hartigan（1977）［13］中描述过，在一维情况下，类似的想法打破了链路上的最小生成树，使得大量的相邻小链路将两个数量相邻的小链接中的至少一个用作检验统计量。同样地，在所有不相交的单个连接集群对（Hartigan，1985）［14］之间取较小的集群的最大。

2 超像素

超像素由一些位置相邻，颜色、亮度、纹理等一些特征相似的像素点组成的小区域，这些小区域都保留了进一步分割图像的有效信息，且一般不会破坏图像中物体的边缘信息。一般用SLIC算法生成超像素。我们的方法初始阶段需要计算大量的超像素，这些小的、紧凑的和视觉上同质的区域中的图像的超分割。基于文献［15］中的比较结果，SLIC超像素分割提供了一个快速有效的选择，因此我们在本文使用此方法对图像做初分割。

2.1 SLIC（Simple Linear Iterative Clustering）算法

首先将RGB颜色转换为五维的CLE-LAB颜色空间，除了记录LAB颜色空间下的像素点还有该像素点的坐标（x，y）。

算法实现过程：对于包含有N个像素点的图像而言，如果对这幅图像聚类为K个超像素块（该算法只设置一个参数，预分割的超像素块的数量），每个超像素块的大小为N/k，若每个超像素块的长和宽分布均匀，那么每个超像素块的边长为（N/k）^0.5。

为了避免所选的像素中心点不在边缘上或者噪声点这中不合理的像素点，将找到的中心点和周围8个像素点进行比较，找到其欧氏距离最小的点作为中心点。

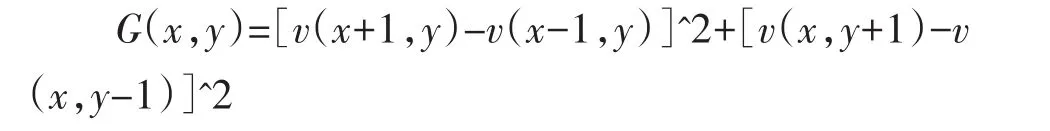
接下来用K-means算法进行聚类。

将某一区域中独立的像素点被标记归属于某一快超像素中但是没有合并，则需要重新归类，找到与其相邻的最大的超像素块，来保证每个超像素快的完整性。

SLIC算法的优点，生成的超像素如同细胞一样紧凑整齐，邻域特征比较容易表达；不仅可以分割彩色图像还可以分割灰度图像；默认情况下只需要设置一个预分割的超像素的数量；在速度、生成超像素的紧凑度、轮廓保持方面都比较理想。

3 Dip-dist算法

Dip-dist算法用于评估数据集的聚类结构［16］，即检测一组数据是否为单峰分布，用于图像分割则是将要合并区域的质心被用来决定合并所产生区域的单峰性，最早的Dip-dist算法它首先要定义区域间的相似性（或距离）度量（例如基于平均颜色值）［17］。它的标准依赖于观察者的概念，观众是一个数据对象，通过考虑观察者到其他数据对象成对距离的集合来决定组的单峰性，然后使用单峰检测来测试这组数据的密度以获得单峰性。更具体地说，如果我们数据集的质心视为观察者并形成一个向量，其分量是观察者与所有数据点的距离，那么这个距离向量的值的分布就可以揭示关于聚类结构的信息。

在单一集群的情况下，距离的分布预计是单峰的，在两个、甚至多个集群的情况下，距离的分布应该呈现出两种不同的模式，单峰或者多峰。每个模式包含每个集群的质心到所有数据点的距离。因此对距离矢量的单峰性检测将提供关于此集群的聚类结构。

直观地看，在边界处的观看者，其单峰性更明显。所以我们将该集合数据集的质心作为单独的观察者，计算其到每个观众的欧式距离。

本文中我们提出的是以四个观察者开始，若四个不能合并，则减少为三个至两个。以两个观察者为例，这两个观察者是被测试用于合并的两个像素组的质心（平均特征值），更具体地说是为了合并而测试的像素组，R是由R1和R2的并集得到的像素组。我们首先计算R1和R2的特征空间中相应的质心C1和C2。然后形成包含C1与R中的每个像素之间的特征空间中的距离的集合D1以及包含C2与R中的每个像素之间的特征空间中的距离的集合D2。接下来使用D1和D2检查集合单峰性，如果两个集合都是单峰的，则区域R被认为是单峰的，并且R1和R2的合并认为是成功的。若果发现集合D1和D2中至少有一个是多峰的，则区域R被认为是多峰的，并且R1和R2的合并失败。

4 实验结果

图1和图2展示了两块图像基于Dip-dist分割结果的单峰检测，图1检测的结果是单峰，证明两块图像可以合并，图2检测的结果是多峰则两块图像不能合并。合并的过程是以增量聚类的过程进行合并，即通过增量聚类的过程导致更大的同质区域。图3和图4展示的是三块图像合并的结果，图5和图6展示的是四块图像合并的结果。

图7（a）和图7（b），展示的是对一副图像进行初分割和最终分割的结果。图7的图像来自众所周知的Berkeley图像数据集，为了测试我们所改进的方法，所选的图像包含了各个颜色、物体。对于SLIC算法，从图7（a）可以看出，SLIC分割算法在合并具有相似视觉物体的方面是很成功的。图7（b）是我们所提出的基于Dip-dist算法的改进。

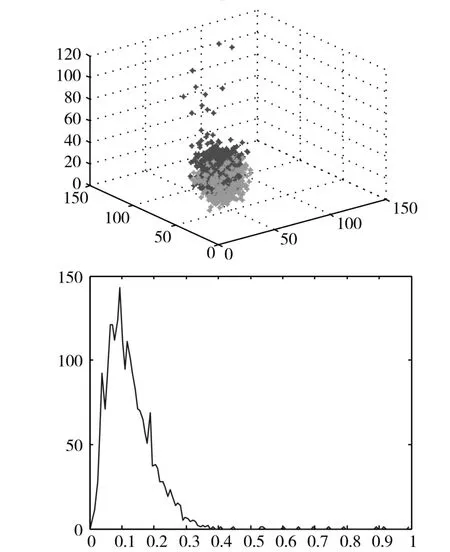
图1 两块图像合并检测结果——可以合并

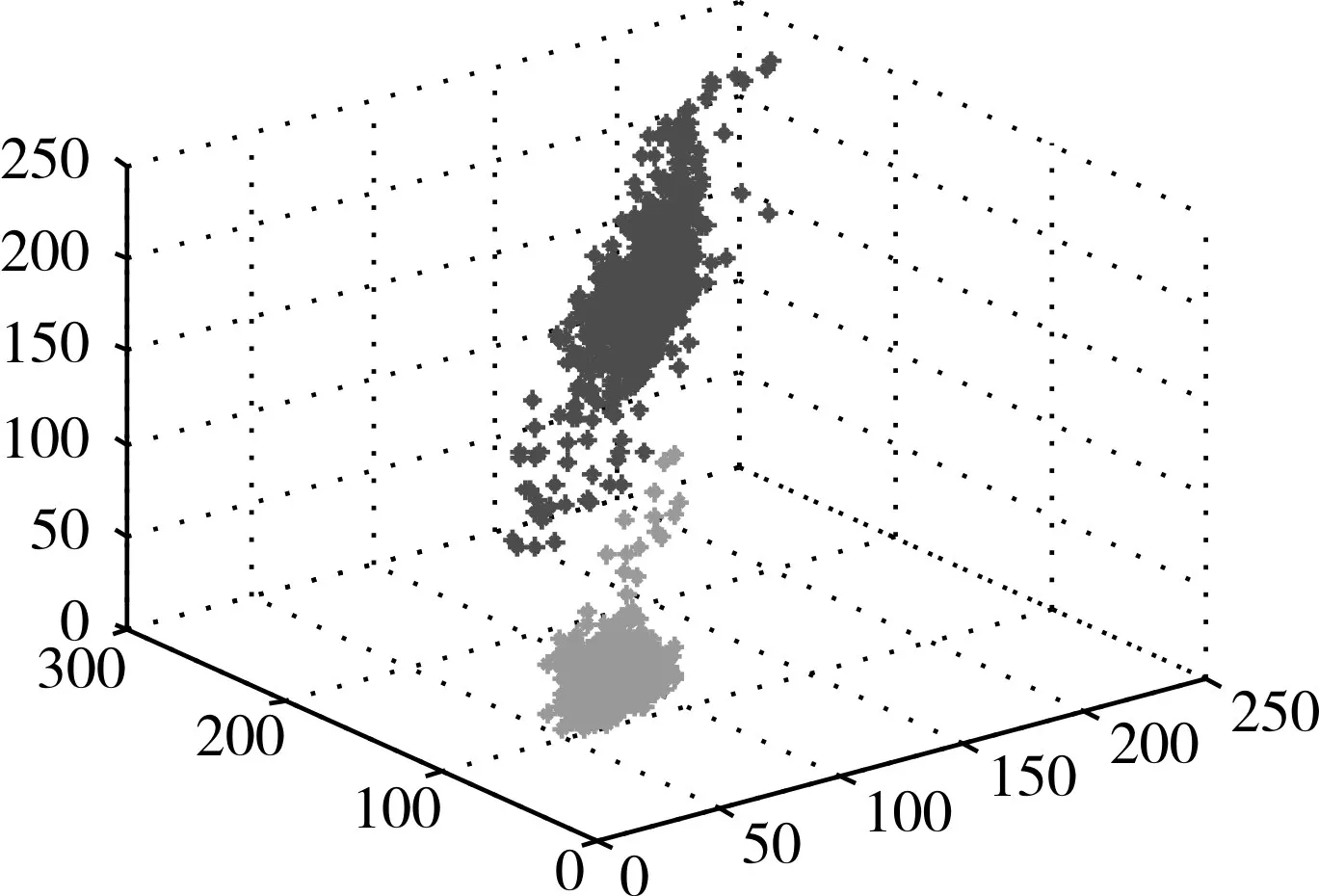
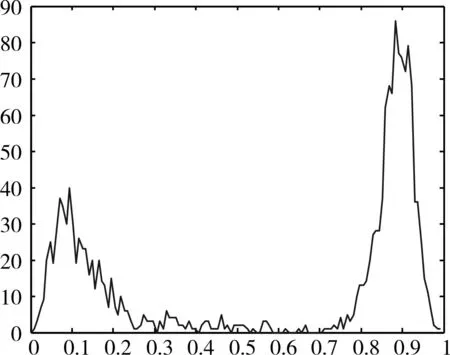
图2 两块图像合并检测结果——不可以合并

图3 三块图像合并检测结果——可以合并

图4 三块图像合并检测结果——不可以合并

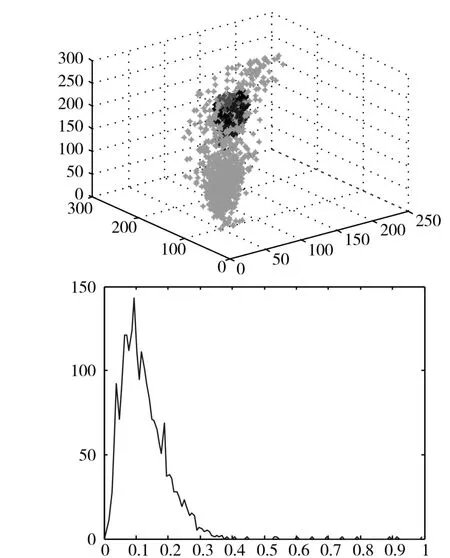
图5 四块图像合并检测结果——可以合并

图6 四块图像合并检测结果——不可以合并

5 结语

初始化做的超像素分割在速度和边缘保持上都比较理想，所以为我们提供了一个快速有效的选择，我们选择的颜色空间是CLELAB，为我们提供五维的颜色的空间（l，a，b）以及像素点的坐标值（x，y），超像素的数量作为SLIC颜色和空间差异的权重因字子。因此像素的特征向量是（l，a，b）向量，一个区域的质心特征向量包括（l，a，b），质心的特征向量到像素点的特征向量的距离是它们的欧氏距离。

图7 图像初始分割和最终分割结果

本文证明了相比于Dip-dist算法，速度上以及分割的正确性都有明显的提升。本文将SLIC超像素分割的结果进行多块区域合并，并将合并的结果以直方图的形式表示，只需要检测一次单峰性。首先进行四块区域的合并，分别找到每块区域的质心，再计算其中一个质心到整个四块区域的像素点的欧氏距离，欧氏距离以直方图的形式表示，更明显地表达数据集的聚类结构。若四个直方图中有一个是呈多峰状的则这四块区域不是同质性的。则接下来需要判断三块区域，同样的方法，若三块区域都呈现单峰状，则通过聚类的过程导致更大的同质区域。