基于网格和密度比的DBSCAN聚类算法研究*
徐红艳 普 蓉 黄法欣 王嵘冰
(辽宁大学信息学院 沈阳 110036)
1 引言
随着大数据时代的到来,数据量的不断膨胀,如何有效地分析这些海量数据已经成为了目前研究的热点和难点。聚类分析能够有效地从海量数据中提取出有效信息[1],DBSCAN 算法(Density-Based Spatial Clustering of Application with Noise)就是经典的基于密度的聚类分析方法[2]。此算法能在含有噪声的数据中识别出任意形状的簇,能够有效地识别出异常点,因而在文本分类[3]、社区发现[4]、垃圾邮件识别[5]等领域都得到广泛的应用。
DBSCAN算法具有很多优点,但也存在着难以发现密度相差较大的簇的缺点。众多学者对该算法进行了深入的研究和改进:Kai[6]等提出一种基于可变类簇的密度比聚类算法,使得当类簇间密度差相差较大时,能够使用单一的阈值就能够达到比较理想的聚类效果。然而该聚类算法需要手动输入的参数过多,输入参数对聚类结果影响较大。Rodriguez[7]等提出DPC聚类算法,它是一种依据快速搜索与密度峰值共同研究发现的,该聚类算法能够有效地检测出任意一种形状的簇,但该算法需要计算局部密度和数据点之间的相对距离,计算量较大。冯振华[8]等提出了一种贪心的DBSCAN改进聚类算法名为greedy DBSCAN,采用贪心策略自适应地寻找Eps半径参数进行类簇发现,但该算法需要手动输入密度阈值,且聚类效率还有待提高。蔡颖琨[9]等提出了一种能够屏蔽参数敏感性的DBSCAN改进聚类算法,通过考察类簇间的连接信息并记录、分析这些连接信息,从而达到屏蔽邻域半径参数Eps敏感的目的,不过该算法未能解决参数Eps自适应确认的问题。
针对上述问题,本文提出了基于网格和密度比的DBSCAN聚类算法,它根据网格和密度比来解决实际问题。此算法使用网格划分的技术将数据空间进行粒化,快速找到数据点密度值的“峰值”和“低谷”,以确定合适的密度阈值,以纠正由于输入密度阈值τ不当造成聚类结果不佳的问题;最后对粒化后的数据空间进行密度比聚类。
2 相关研究
2.1 DBSCAN算法
DBSCAN算法的主要思想是:给定一个未被聚类的点,如果它Eps邻域内的密度阈值不小于MinPts,则这个点是核心点。再考察它邻域内的其他点,以同样的方式判断其是什么点,一直到所有的点被遍历到。由于该方法只对核心对象的邻域密度进行扩展,因此对于那些形态不是很规则的簇,该算法的聚类效果较好。
尽管此算法具有能够有效识别噪声点,并且能够识别任意形状的簇,且聚类结果几乎不依赖于遍历顺序的优点[10]。但是它也存在较为明显的缺点:难以发现密度相差较大的簇。由于参数Eps和MinPts是全局唯一的,所以DBSCAN算法只能发现密度近似的簇。此外,如果类间距离差别比较大,算法结果也会产生影响,容易产生偏差。
2.2 基于网格的聚类算法
这种聚类算法的工作原理是对数据空间进行粒化,具体的操作是将数据空间进行划分并分割为有限个网格子单元,由此形成网格结构,在该网格结构的基础上进行数据分析[11]。该聚类算法只是和网格划分出的个数有关,而与运行时的时间复杂度和数据点的个数无关。STING算法[12]是一种基于网格的多分辨率的聚类技术,基于网格的聚类方法对数据输入顺序不敏感,可扩展性也较强。
与其他聚类算法相比,STING算法有如下优点:
1)查询操作和基于网格划分的计算是相互独立的,因为计算所需的信息只依赖于相互在每个单元中的统计信息,而不依赖于查询。
2)STING算法在网格结构上也优于其他的聚类算法,尤其是在动态更新和处理并发进程的方面;
3)STING算法的效率与其他聚类算法相比也有了很大程度的提高,使用该算法只需对数据库的单元进行一次扫描就可以通过计算得到相应的信息,因此聚类的时间复杂度是O(n)(n为数据对象的个数)。在层次结构建立后时间复杂度可表示为O(g)(g是最低层网格单元的数目,g< 此算法也存在下面的不足: 1)STING算法进行聚类分析时使用的是多分辨率分析的方法,使用STING算法时聚类结果的质量是由所划分层次结构的底层粒度来决定的。若它太细,则会使聚类的处理难度加大,采用STING算法的优势将无法充分发挥;若底层粒度太粗,则聚类质量会大打折扣。 2)此算法在父亲单元的构造上忽略了其孩子单元和其相邻单元之间的关系,会造成簇的边界不是水平的就是竖直的,不包含斜向的分界线。 3)尽管在选取合适聚类粒度的情况下,STING算法能够快速对数据集进行聚类处理,但是会在一定程度上牺牲聚类的准确度。 为了避免DBSCAN算法将低密度簇中的数据点错误地归类为噪声点,Recon-DBSCAN聚类算法[13]将密度比估计代替密度估计,其数据点的密度是该点的密度相对于邻域平均密度进行归一化处理后的值。类簇实际为被低密度区域分隔开的局部高密度区域,Recon-DBSCAN算法使得高密度簇通过归一化后变为密度较低的簇,且低密度簇通过归一化后也变为密度较高的簇,归一化后的数据能够被全局阈值τ区分开来。 图1(a)仅用DBSCAN单一阈值就能够将三个簇进行区分;图1(b)中的情形利用传统的DBSCAN聚类算法使用单一阈值无法将所有类簇区分开来,若取阈值τ1则簇C3中的所有点都被归为噪声点;若取阈值为τ2则簇C1和C2将会归为同一个簇;图1(c)所示为用密度比估计替换DBSCAN算法中的密度估计,通过对数据点的密度进行归一化处理,使得可用单一的全局阈值对所有簇进行有效区分。 Recon-DBSCAN聚类算法采用数据点的密度比估计替换该点的密度估计,然后再对数据集进行聚类,从而使低密度集群不被DBSCAN算法错误地归于噪声点。但是,Recon-DBSCAN聚类算法也存在缺点:聚类时需要用户手动输入的参数过多;得到最佳聚类结果的过程是一个不断尝试的过程,无法自适应地得到聚类阈值。 图1 数据高斯分布图 针对上述聚类算法中存在的问题,本文使用GRDBSCAN(Grid and Density-ratio Clustering Algorithm based on DBSCAN)聚类算法来处理这些问题,此算法是依据网格的划分和密度比的计算来解决实际问题。首先通过自适应多分辨率的网格划分的思想把数据划分到多个网格空间中,利用所划分的网格加快查找到类簇的峰值和低谷,再利用密度估计来计算密度比,从而实现自适应地确定密度阈值τ和使用该全局阈值识别数据集的基于密度比聚类的目的。 GRDBSCAN算法框架如下: 本文通过划分网格将数据空间进行粒化,旨在快速找到数据点密度值的“山峰”和“山谷”,以确定基于密度比聚类算法中合适的密度阈值。该算法主要分为网格粒化数据空间、确定阈值和网格单元聚类三个核心环节。 图2 GRDBSCAN框架 将数据空间进行粒化的目的是为了压缩数据,降低算法的时间复杂度。STING网格划分对数据进行粒化,以网格单元数据的统计信息代替原始的数据点,从而达到数据压缩的目的。数据粒化的算法为 算法1:数据粒化算法 输入:数据样本集D 算法步骤: 1)将数据样本D归一化到d维空间中; 2)设定顶层划分尺度为l=,对数据空间进行各个维度的划分,且顶层网格单元与全局数据空间的信息相一致; 3)从顶层至底层逐渐粒化,第i+1层的子单元为第i层单元的1/4,当底层网格lk≤2ε时停止。 4)扫描整个数据集,把数据集中的每个点都放入网格划分后的数据空间中,并记录网格单元的信息(如:网格单元密度、最大值、最小值等),记录网格单元的个数为n。 一个服从高斯分布的数据集,若存在密度极大值点,则越靠近聚类中心的点密度值越大,越是处于边界的点,密度值越小,反映在网格密度中也存在同样的分布规律。因此能够对划分后的网格子空间进行信息的统计,数据压缩等操作,选取网格子单元的逻辑中心点代表该网格,对数据空间进行压缩。压缩后的数据点个数与网格个数相同,通过数据空间的压缩,可以大大减小由于计算数据点之间的相对距离的计算量。 该步骤是为了在粒化后的所有网格单元中快速找出极值点。首先,扫描整个数据集,即将网格单元中数据点的个数作为网格单元的频度;然后,利用聚类中心网格单元与其他聚类中心网格单元的距离大,而与其网格单元类簇中其他网格单元的距离小的思路,确定极大值点;最后,利用极小值点为极大值点连线上的密度最小点,得出密度阈值。算法步骤如下。 算法2:确定阈值算法 输出:密度阈值τ 算法步骤描述: 1)计算网格单元的密度ρi并降序排列 2)计算网格单元间的相对距离距离σi,用hi为降序排列的ρi标记,即ρh1≥ρh2≥…≥ρhn;两网格单元a和b的欧氏距离定义如式(1)所示[14]: 3)将网格单元的局部密度和相对距离可视化,如图3。 图3 网格局部密度和相对距离可视化 4)由图3,得出网格空间极大值点 5)极小值点为极大值点连线上的密度最小点,即得出极小值点的集合,选取极小值点的集合中的最大值,其密度即为密度阈值τ。 图4 三种高斯分布组成的二维数据集估计密度分布的可视化 考虑使用一个全局密度阈值MinPts来区分所有的类簇。如图4所示,为了将类簇集合C={C1,C2,C3}区分开来,则阈值的取值 MinPts大于 p(g12)时方可将三个类簇都区分开来。然而这样的划分方式下,簇C3中的很多点都会被归类为噪声点,达不到很好的聚类效果。 更加糟糕的情形是,若g12处的局部密度p(g12)大于p3处局部密度p(p3)的情况。若取密度阈值MinPts>p(g12),则C3中的所有数据点都会被归类为噪声数据,聚类的结果只能得到两个类;若取密度阈值 MinPts<p(p3),则簇 C1和 C2将会被归为同一类,仍然只能得到两个类。如果能够用某种方式,能够使得密度大的区域的密度降低一些,同时使得密度小的区域的密度更大一些,使得整个数据空间的数据对象密度分布更加均匀,减小类簇间的密度差异,使得那么密度平均化之后的是数据集能够被一个全局阈值τ区分开来。 由基于密度比的DBSCAN算法的聚类过程可知,知道基于密度比的DBSCAN聚类算法需要输入的参数包括ε,η和τ三个参数,通常为了方便衡量ε和η之间的差距,令η=λε,λ∈[1.08,1.09,…,1.16],由此确定不同λ值对聚类效果的影响。如果能够自适应地确定密度比阈值τ,则只需要根据λ值确定不同的邻域密度比与其准确度之间的影响。 算法3:网格单元聚类算法 输出:聚类结果C 算法步骤描述: 1)计算各网格单元的密度比; 2)根据算法3得到的极大值和极小值,得到它们的密度比,选取簇谷集合密度比的最大值gij为密度阈值τ; 3)根据算法1对压缩后的网格单元E进行DBSCAN聚类,根据阈值τ剔除噪声网格; 4)得到最终聚类结果C。 本文提出算法的时间开销包括计算网格粒化、网格单元的统计信息、网格单元的相对距离和对压缩后的数据空间进行聚类。其中时间开销最大的就是求网格单元的距离。算法的时间开销具体如下: 1)划分网格时产生聚类的时间复杂度为O(n),它是通过STING扫描数据库一次计算单元的统计信息而得到的,层次结构建立后,查询处理时间为O(R),R为底层网格单元的数目; 2)查找簇峰和簇谷的过程需要求得相对距离,此过程的时间复杂度为O((n/ε)2); 3)基于密度的DBSCAN聚类,时间复杂度为O(R2); 总的时间复杂度如式(3): 由于R是一个远小于n的数,所以算法的时间复杂度为O((n/ε)2)。 算法的空间复杂度只与网格单元的数目有关,因此算法的空间复杂度为O((n/ε)2)。 本文实验所采用的计算机硬件配置为AMD E2处理器、8GB内存;实验的软件环境为Windows8操作系统,采用Matlab 2014b编译环境。为了证明本文所提算法的可行性和有效性,以UCI数据库[15]中 4个公用数据集s1、s2、Iris、Segment为测试数据集,设计了以下实验进行验证。 以UCI上的一个人工数据集s1进行实验,取阈值ε=0.1523,求得τ=0.8955时,以分类模型的精确率和召回率的调和平均数F值来度量本算法的精确度,得出λ和F值的关系如图5所示。 图5 λ与F值间关系图 分别对另外3个数据集测试λ与F值之间的关系,得出当λ=1.1时,算法效果最好。 数据集s2为一个包含1500个数据点的人造数据集,ε=0.0108时,求得τ=0.8820。聚类结果对比如图6。 图6 聚类结果对比 以UCI数据集上的四个人工数据集Iris、Segment、s1、s2作为实验对象,聚类运行时间比较如表1。 表1 算法时间复杂度对比 单位(s) 由表1可以得出,随着数据点个数增多,三种算法下运算时间都增大。由于本文算法与DPC算法都需要计算,运算时间较传统DBSCAN算法更长。但DPC算法计算更复杂、需要被计算的数据点更多,故运算时间较长。 实验3以UCI数据集上的四个人工数据集Iris、Segment、s1、s2 作为实验对象,选取合适的参数,求得最佳的F值,与DBSCAN算法、DPC算法聚类准确度F值比较如表2。 表2 F值比较 F值能够度量一个算法性能的好坏,当F值越大时,算法效果越好。通过以上实验可知,本文算法在选择合适参数的情形下,具有较高的F值,明显优于DBSCAN算法,且与DPC算法相差不大。 基于密度比的聚类算法对于密度分布不均匀的簇有较好的聚类效果,因此本文提出GRDBSCAN聚类算法,它依据网格和密度比的计算来提高密度分布不均匀的簇的聚类效果。同时它较比其他的聚类算法有了新的优点,其一压缩了数据空间,在此基础上进行聚类,提高了运算效率;其二能够自适应地得出聚类的密度阈值,降低了因参数选取不当造成的聚类效果不佳的问题。下一步研究如何针对海量数据进行聚类,以及利用分布式Spark平台进行聚类。2.3 基于密度比的DBSCAN算法——Recon-DBSCAN

3 基于网格和密度比的DBSCAN聚类算法
3.1 算法思想与框架
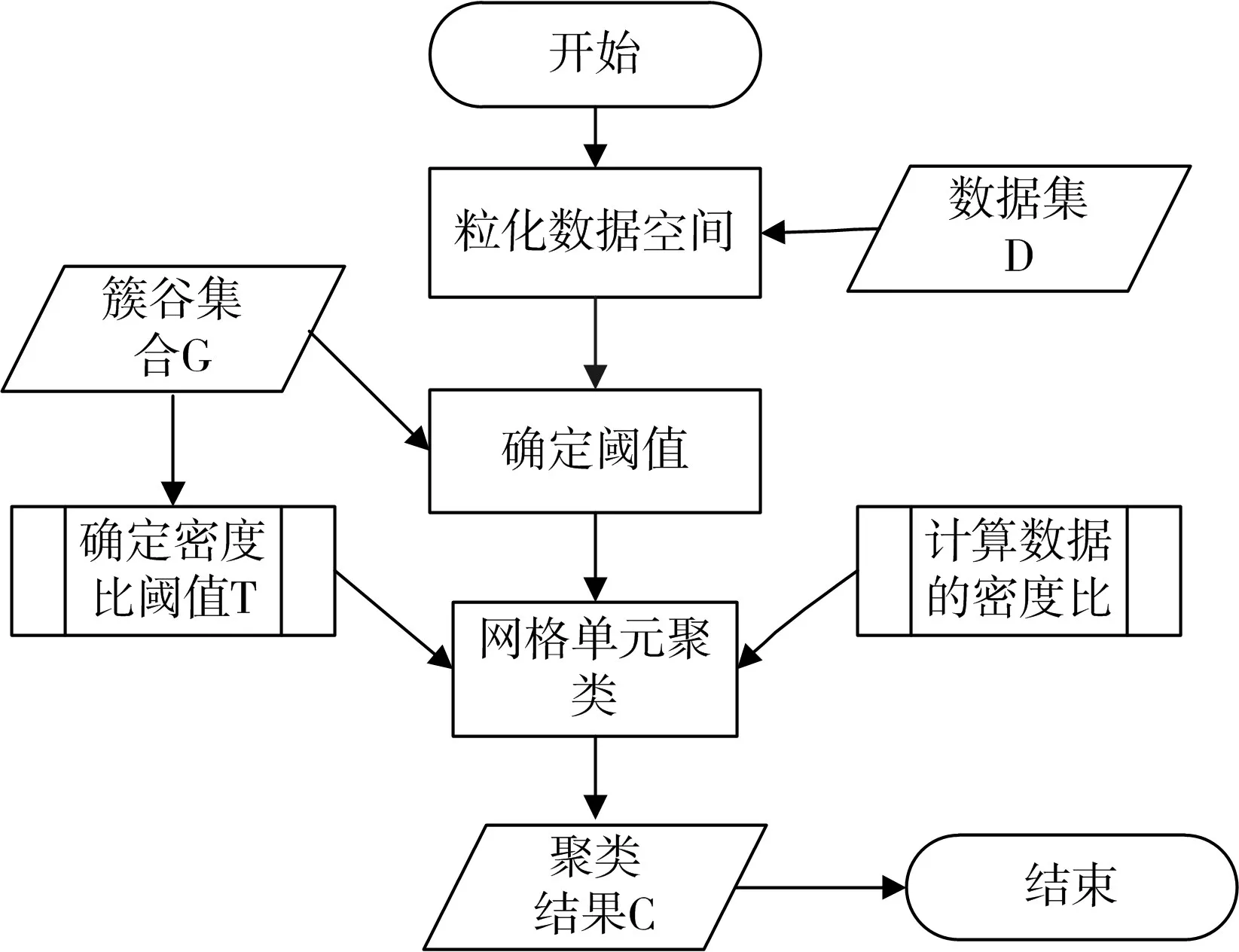
3.2 网格粒化数据空间

3.3 确定阈值

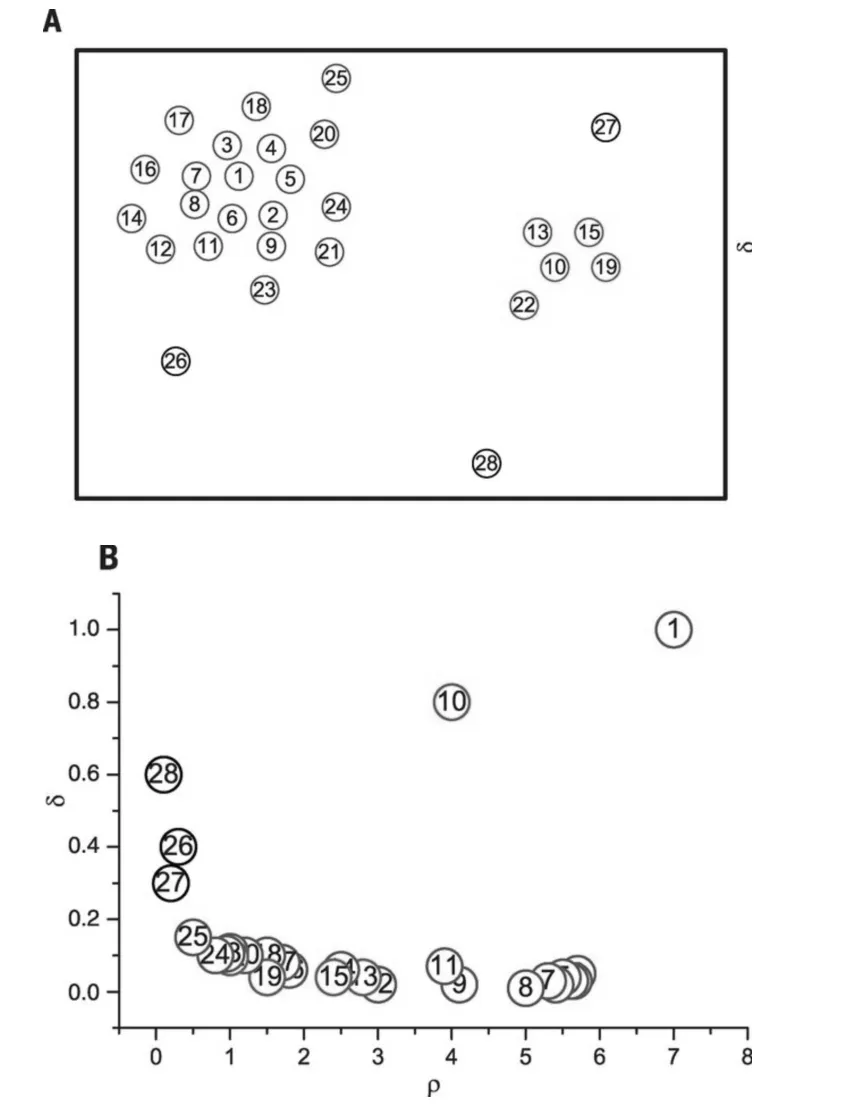
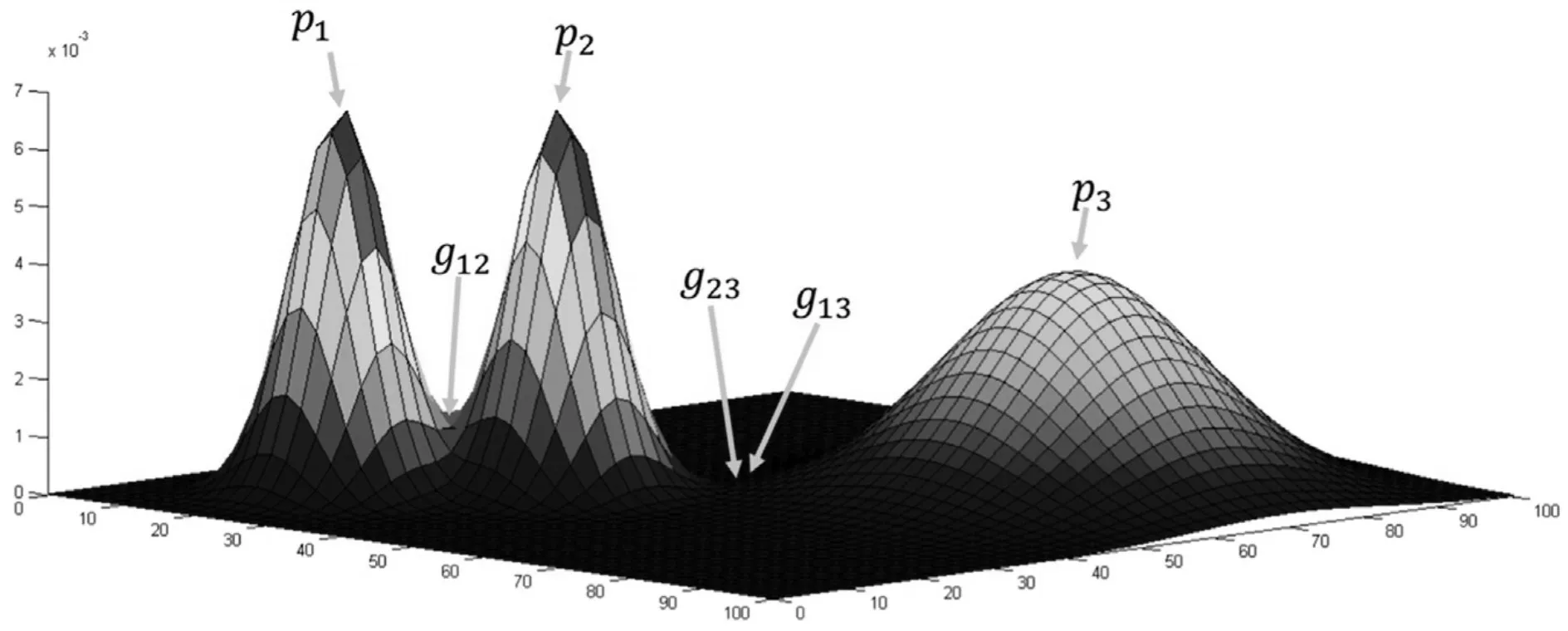
3.4 网格单元聚类

3.5 算法复杂度分析
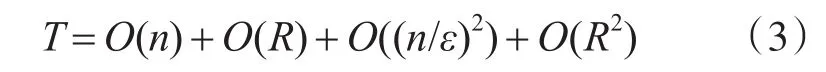
4 实验与分析
4.1 密度比值λ对算法的影响
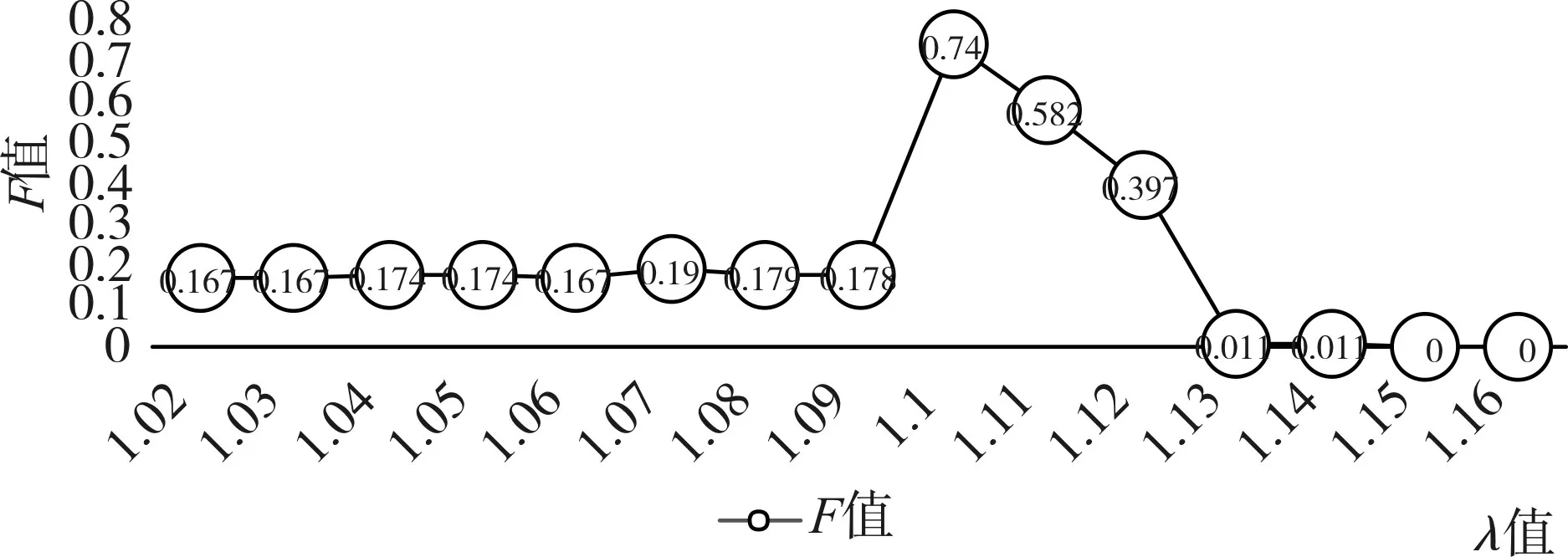
4.2 聚类结果对比
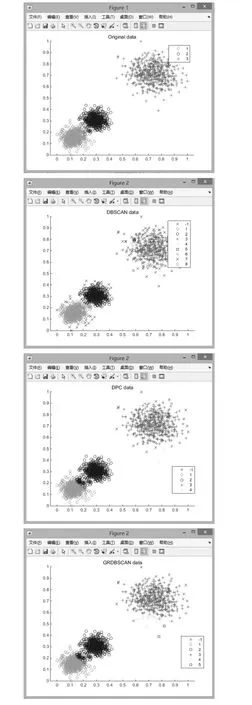
4.3 聚类运行时间比较
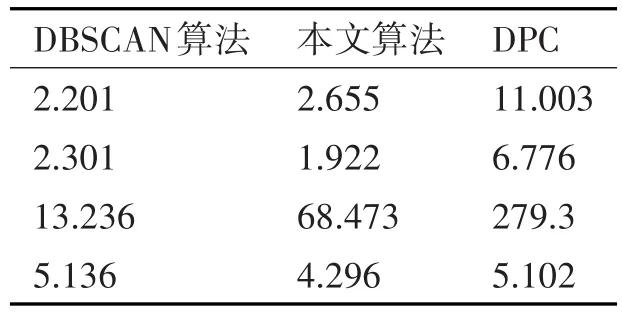
4.4 聚类准确度F值比较
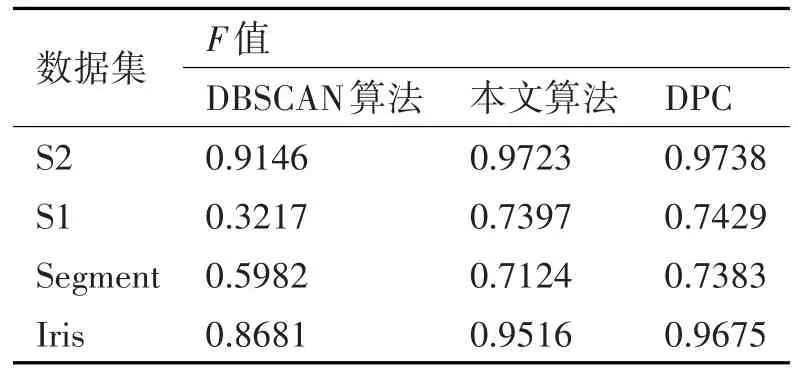
5 结语

