模糊最小二乘大间隔孪生支持向量回归机*

王怡芮 朱志祥

（西安邮电大学物联网与两化融合研究院 西安 710061）

1 引言

近几年，支持向量机（SVM）［1］已经被广泛应用在分类和回归领域。SVM的理论基础是VC维理论和结构风险最小化原则。相比于人工神经网络等其他机器学习算法，SVM有如下优势：1）SVM解决一个带约束的二次规划问题，能够得到唯一的最优解；2）SVM基于结构风险最小化理论原则，具备更好的泛化性能。通过核函数的引用［2～3］，SVM成功地解决非线性问题，受到了专家学者的广泛关注。然而，SVM对于大数据量的模型训练，存在时间复杂度较高的问题。SVM模型训练的时间复杂度为O(m3)，m为训练样本的规模。

Jayadeva等提出了一种用于解决分类问题的新算法—孪生支持向量机［4］（TWSVM）。TWSVM算法的灵感来源于GEPSVM，不再类似于SVM训练获得两个平行的超平面，TWSVM通过解决两个规模较小的二次规划问题以此获得两个不平行的超平面。通过计算分析，在数据集规模相同的情况下，TWSVM的训练速率较标准SVM的提升4倍。2010年，Peng将TWSVM从解决分类问题扩展到回归问题，提出了孪生支持向量回归机［5］（TSVR）。2012年，Xu Yitian和Wang Laisheng提出了加权孪生回归机（weighted twin support vector regression，weighted TSVR）［6］，通过赋予不同位置的样本不同的惩罚力度，使得回归机能够在一定程度上避免过度拟合问题，提升模型的泛化能力。为了减轻计算负担，2013年，Huang HJ和Ding SF等提出了最小二乘孪生支持向量回归机［7］（Primal least squares twin support vector regression，LSSVR）。

近些年的研究使得TSVR有了不同方向的进展［8～16］，但是这些研究所考虑的每一个训练数据对于生成超平面的贡献和作用是相同的，没有反映出数据在真实空间中的内在分布情况［17～18］。同时，为了进一步提高模型的训练效率和模型精度，本文提出一种基于最小二乘的大间隔模糊孪生支持向量回归机（LSFTSVR），在目标函数中对不同数据所对应的经验误差进行密度加权，密度加权值在真实空间中采用KNN算法进行计算，并对密度加权值进行归一化。通过实验结果比较，发现所提出的LSFTSVR相比于weighted TSVR具有更高的精确度。

2 TSVR

为了提高普通SVR的计算速度和泛化性能，Peng提出了一种有效的回归函数，称为TSVR，它是通过求解以下两个QPP问题得到的。

对TSVR进行简单介绍。假设一个大小为m的数据集S表示为

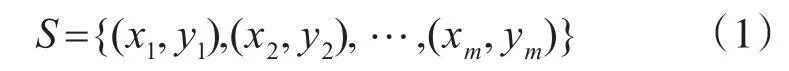
其中，xi∈Rn，i=1，2，…，m，n 。目标是通过构建两个优化问题获得两个函数来预测无输出的实例。与传统TWSVM构建思想类似，TSVR将在训练数据点两侧产生一对不平行的函数，分别确定回归函数的ε不敏感上、下界。对于线性情况，TSVR通过训练数据的ε1不敏感下界：

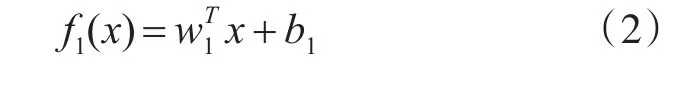
与ε2不敏感上界：

确定最终的预测回归函数。最终预测函数表示如下：

式（2）和（3）对应的函数的求解可以通过求解下面的一对二次规划问题：

通过拉格朗日变换，引入α和γ，将式（5）和（6）转化为如下对偶形式：

3 模糊隶属度和间隔分布函数

3.1 模糊隶属度

在普通εSVR中，回归函数相比分类机而言对孤立点更加敏感，图1表示加入孤立点前后，回归间隔变化的示意图，从图中可以发现，由于孤立点的加入回归间隔发生了很大的变化，整体向靠近孤立点的方向靠近，由此产生误差。

图1表明，设计SVR隶属度函数的过程中，需要考虑到以下三点：第一，设计的隶属度应该能准确判断出噪声孤立点，并将它从训练集中舍掉；第二，离回归线越远的数据点较回归线附近的样本点对回归线构建的影响越大，若数据点不重要，应该赋予其较小的隶属度值；第三，越靠近预测点的训练样本点对最终的回归结果影响越大，因此应该赋予靠近预测点的样本点较大的隶属度。

图1 加入孤立点前后的回归线

由于上述原因，回归机的隶属度设计不再单纯仿照分类机通常依据距离设定。参考FSVM中隶属度的模型原则，将其引入SVR中。引入基于密度的模糊隶属度函数si(i=1，2，…m)，将给出如下定义：

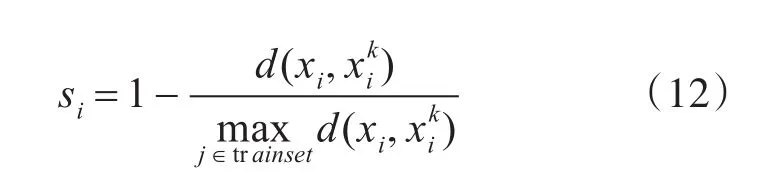
参考k近邻的思想：如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。则表示在原始数据空间中，样本数据点xi周围第k个邻近的点，d(xi，)是xi与间的欧式距离。

本章为回归机设计的隶属度函数以密度为原则，改善了基于距离法的隶属度仍然对异常点敏感的问题。通过引入k近邻的思想，为了体现样本真实分布情况，衡量了训练数据点之间的相对密度。各个数据点对应的隶属度值si通过计算各个样本数据点与其对应的第k个近邻点之间的距离和所有训练样本距离中的最大值之比获得，即式（12），同时0＜si≤1。相比单纯依靠距离法的隶属度函数，基于密度的隶属度函数，对于大多数数据点紧凑，只有少数异常点的情况，能更加准确地反映训练数据集的内在分布情况，因此能够很大程度地减小噪声孤立点这类异常点对最优超平面的负面影响。

对数据点进行如上的操作后，训练数据集S中每个数据点xi都被赋予对应的隶属度值si，将si组成m×m大小的对角矩阵W=diag(2，…，sm)，其对角线值为对应的隶属度值。

3.2 间隔分布

理论研究表明［16］，间隔分布对于模型的影响通过一阶和二阶统计特性来表现。本文中，采用了间隔均值和间隔方差来代表这两个统计特性。通过文献［17］，每个训练数据(xi，yi)所对应的几何间隔为μi=yi(wTxi+b)。可以计算间隔均值和间隔方差。Y为l×1的列矩阵，表示样本输出值组成的矩阵；e为所有元素为1的l×1列矩阵。考虑f1以及vi=[wi，bi]情况下，可以获得如下的间隔均值和间隔方差：

3.3 模糊最小二乘孪生大间隔支持向量回归机

首先在标准TSVR的基础上，凭借间隔分布的作用提高模型的泛化能力。同时考虑到结构最小化原则，提出新的回归算法。在该算法中，为了减小噪声孤立点对模型超平面构建的影响并提高训练速度，引入模糊隶属度函数和最小二乘方法。然后将隶属度矩阵W引入到目标函数中，形成新的二次规划问题，线性模糊最小二乘孪生大间隔回归机模型如下：

式（17）将约束条件代入目标函数中，对w1和b1分别求导，并令其为0：

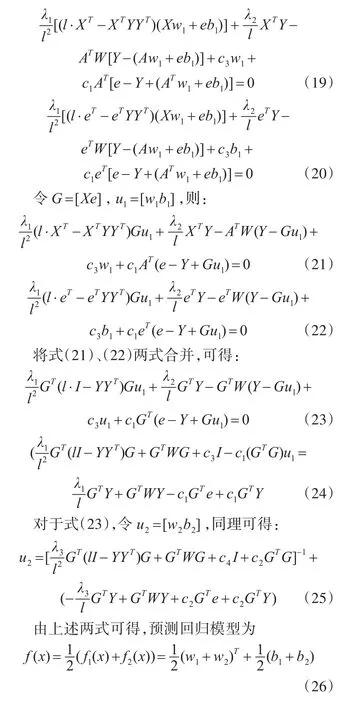
4 算法分析及实验仿真

4.1 评价标准

为了评价回归机的优劣与否，需要通过一些指标体现回归机的各项性能。yi表示第i个样本实际输出值，y^i表示第i个样本预测输出值，yˉi表示第i个样本输出平均值，m是测试样本总数。介绍常用的6种性能指标如下：

1）和方差（SSE）

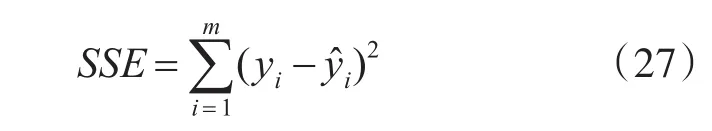
即测试样本拟合输出和原始输出误差的平方和。其中，SSE表示预测精度，即SSE越小，模型拟合数据的能力越好。但是，如果测试样本中噪声干扰较大，则太小的SSE可能导致过拟合现象。

2）SST

即原始数据和均值之差的平方和。其中SST是由噪声或输入值变化引起的测试样本的改变。

3）SSR：

其中SSR代表构造模型的解释能力。SSR越大，它从测试样本中获得的统计信息就越多。

4）均方根误差（RMSE）

其中，RMSE与SSE相同，代表预测误差。RMSE可以评价数据的变化程度，RMSE越小，说明该模型的拟合实验数据能力越强。RMSE能很好地反映出模型的精密度。

5）归一化均方误差（NMSE）

其中，NMSE是误差平方和与测试样本的平方偏差之和的比值。NMSE越小，回归的性能越好。

6）R2

R2表示可预测的偏差平方和与测试样本的平方偏差的实际总和之比。大多数情况下，较小的NMSE意味着预测和实际值之间存在着更好的一致性。但是，较小的NMSE通常伴随着R2的增加。

4.2 LSFTSVR实验结果与分析

为了验证本章提出的LSFTSVR算法的性能，对LSFTSVR算法和Weighed TSVR算法分别在UCI［18］数据库中的数据集进行了测试并对其进行比较分析。本章中的算法均使用Matlab 7.11.0的软件编程语言实现，操作系统为Windows7，主频2.5GHz，计算机的内存大小为2GB。实验中采用的7个数据集均来自UCI数据库。为了让两种算法在同一平台上进行比较，在非线性情况中，实验中所用的核函数均为Gaussian核函数 K(x，y)=exp(-μ‖x-y‖2)。为了保证实验的可信度，所有实验均在相同的环境下进行的。为了得到最好的实验结果，所有实验均使用十倍交叉验证找出整个范围内的最佳参数，所有算法参数范围均在{2i|i=-2，…，8}内。同时，为了能够客观并准确地反应实验的结果，实验的最终数据是通过十倍交叉验证方法完成十次实验的平均值。时间是代入最优参数完成一次实验所花费的CPU时间。实验设定c1=c2，c3=c4，λ1=λ3，λ2=λ4，k=15。

4.2.1 人工数据集

在机器学习方面，常用sinc(x)函数测试各种机器学习方法的回归性能。其表达式为

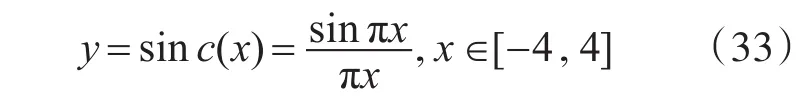
本试验的人工数据是系统生成的200个两类二维数据，选取200个数据中的80%作为训练数据，剩下的作为预测数据。因为每次试验数据选取的80%都是随机的，故本实验的准确率是十次平均准确率的结果。

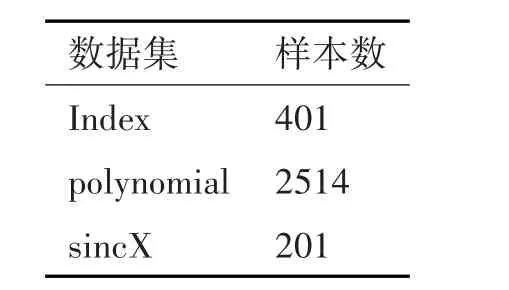
表1 人工数据集的特征

表2 LSFTSVR人工数据集上实验结果

从表2可以看出LSFTSVR能得到比较小的RMSE及NMSE和较大的R2，这说明LSFTSVR的逼近精度比Weighed TSVR的逼近精度好，即LSFTSVR在回归精确度上有较明显的提高。总的来说，LSFTSVR的拟合能力更好。

4.2.2 UCI数据集

为了进一步验证本节所提出算法的各项性能，我们对来自UCI数据库的7个基准数据集进行了实验。回归效果可以从海量数据集中清晰地展示出来。测试样本同样占总样本的80%。表3是标准数据集的特征。

表4是LSFTSVR分别对7个数据集进行10次测试的平均结果。

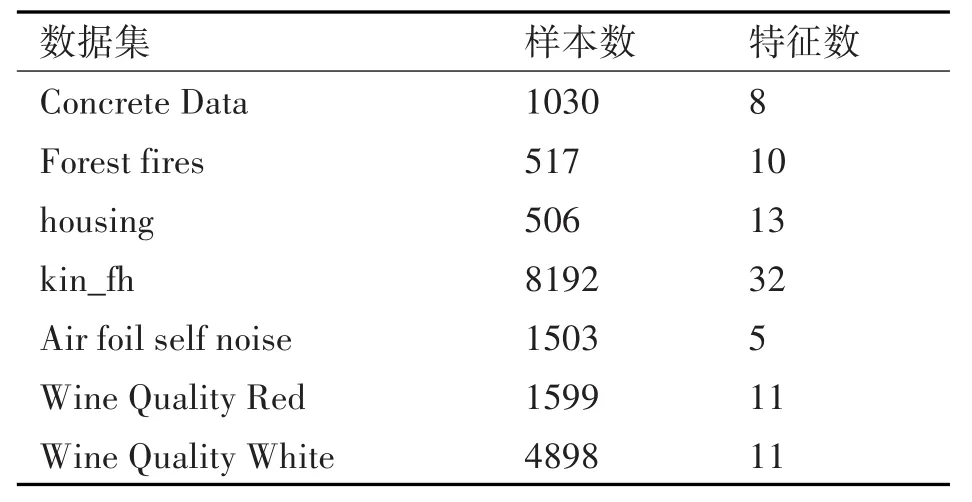
表3 数据集特征

表4 LSFTSVR在UCI数据集上实验结果

表5 LSFTSVR在UCI数据集上训练效率的实验结果

从表4的实验结果来看，在选取的7个数据集中，本文所提出的LSFTSVR算法较Weighed TSVR算法能得到比较小的RMSE及NMSE和较大的R2，这说明LSFTSVR的逼近精度比Weighed TSVR的逼近精度高，在回归精确度上有较明显的提高，验证了所提出的LSFTSVR算法的有效性。从表5来看，相比于标准Weighed TSVR算法，在训练速度上有明显的提高，同时也验证了采用最小二乘思想解决TSVR算法的有效性。

综上所述，本文所提出的最小二乘模糊孪生大间隔支持向量回归机算法通过引入隶属度函数及间隔分布，使模型能够更好地反映训练数据集的内在分布，从而获得了更加精确的训练模型。

5 结语

本文提出了一种新的模糊孪生支持向量回归机，称为模糊最小二乘大间隔孪生回归机（LSFTSVR）。引入间隔分布函数，将标准的模糊孪生支持向量回归机优化目标从经验风险最小化扩展到结构风险最小化，并将最小二乘思想引入到新的模型中。通过对LSFTSVR算法和Weighed TSVR在7个UCI数据集和3个人工数据集上的比较发现，所提出的算法在相关预测参考值上有一定的提高，从而验证了所提出算法的有效性。