关于图论课堂教学的探讨与研究

孙晓玲 杜建伟

[摘 要] 图论是应用比较广泛的一门数学课程，但由于其内容多、理论抽象，学生的学习积极性不高，课堂教学效果往往不太理想。结合作者多年的教学经验，总结了构建图论精彩课堂教学的几个方法。

[关键词] 图论;课堂教学;学习兴趣;学习能力

[基金项目] 中北大学教改项目;山西省青年科学基金（201901D211227）

[作者简介] 孙晓玲（1981—），女，山西广灵人，博士，中北大学理学院讲师，主要从事图论及其应用研究;杜建伟（1979—），男，山西代县人，博士，中北大学理学院讲师，主要从事图论及其应用研究。

[中图分类号] G642.4    [文献标识码] A    [文章编号] 1674-9324（2020）31-0301-02    [收稿日期] 2020-01-10

图论是数学系本科生的一门基础选修课，应用数学专业研究生的一门专业必修课。它在化学、材料学、计算机科学、运筹学、信息与通信科学、社会科学、经济管理学等方面都有着广泛的应用。尤其是近年来，随着网络和计算机技术的迅速发展，图论取得了许多可喜的成果，受到了数学界的广泛重视。但由于图论的内容十分丰富，涉及的面也比较广，且对逻辑推理能力要求比较高，学生在学习这门课程时，往往感到抽象、难以理解和接受，容易产生厌学情绪。因此，教师需要合理设计教学过程，通过有趣、实用、多样的课堂内容，激發学生的学习兴趣，培养学生的主体学习能力。

一、通过“数学游戏”引入概念，激发学生的学习兴趣

在讲图的定义时，可以先让学生动手画一些图，如家族关系图、友谊图、球赛中的比赛关系图、图书馆的藏书分类图等。要求他们用顶点表示人（或物），边表示人与人（或物与物）之间具有的某种关系;然后再引入图论中图的定义，解释图的本质就是一个二元关系（顶点和边的关联关系），这样学生在游戏中便掌握了图的定义，同时也体会到了图论的实用性。

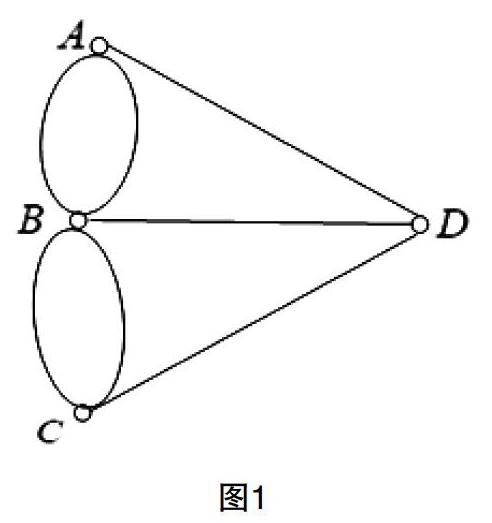
在学习欧拉图的知识时，先介绍著名的格尼期斯城堡七桥问题，然后用顶点表示该问题中出现的陆地和岛屿（分别用A，B，C，D表示），用边表示连接陆地和岛屿的桥，通过建立数学模型将其转化为一个能否一笔画的游戏，即在图1所示的图中，从A，B，C，D四点中的任意一点出发，能否笔不离纸且每条线只能经过一次，最后回到出发点。许多学生在中学时期有玩过一笔画的游戏，在他们看来这是一件很简单的事情，非常愿意去进行尝试，但经过无数次尝试都无法成功时，学生的好奇心就被激发出来了，为什么不能一笔画成？为什么七桥问题是无解的呢？这时教师再来介绍欧拉图的定义和定理，解释不能一笔画的原因，课堂效果会好一些，学生带着好奇心去听课，会更容易理解和接受。

二、纠错教学，培养学生的反思能力

在图论课堂教学中，教师可以有意的设置一些错误。例如，在求连通图K的全部生成树时，可以有意漏掉几种，或者多出一些同构的生成树;在对图进行正常点染色时，某两个相邻顶点故意染上相同的颜色，让学生来纠错。学生在寻找错误的过程中会加深对知识点的理解，认识到问题的本质，同时纠错成功的喜悦之情也会激发学生的求知欲和反思能力。

三、因材施教，实行层次教学

针对不同层次学生的特点及不同奋斗目标，适当增减内容，满足不同学生群体的需求。在给本科生授课时，主要以基础概念、简单的定理证明为主，降低难度，使学生容易理解和接受，同时多介绍一些学生感兴趣的内容，如格尼期斯城堡七桥问题、四色猜想、环球航行问题、中国邮路问题、排课表问题、人员分配问题等。另外，有不少学生要参加全国大学生数学建模比赛，而建模比赛中遇到的许多实际问题（如多阶段决策问题、选址问题、管道的铺设、网络最小费用流问题等）都可以通过图论中的最短道路问题模型来解决，针对这部分同学的需求，详细介绍得克斯特拉（E.W.Dijkstra）算法、Flogd算法和最优化原则，通过有趣的内容和实用的算法模型激发学生的兴趣和求知欲。

给研究生授课时，除了要全面、深入和系统讲授书本知识外，还要补充一些科研工作者的最新研究成果（如现在比较热门的超图、化学图论等），及时更新概念和理论的表达形式，在有限的课时内教给学生最重要的内容。另外，考虑到研究生需要独立从事科研工作，教师在课堂教学中可以适当选取一些章节和学术论文由学生讲、老师听，发现问题共同讨论。在这个过程中，学生会更容易发现自己的问题，同时把主动权交给学生，他们由听众变成参与者后思维会更活跃，不仅学得认真，对知识的理解也更完整。

四、培养学生的合作意识和团体协作能力

在课堂教学中，教师要给学生创造对话和辩论的空间，鼓励他们互动并分享观点。在学习了顶点的度的知识后，将学生分成若干小组，每组成员不少于两个人。先让他们观察一下是否存在两个人在组内有相同个数的朋友，若存在，要求他们利用所学知识证明这个命题。学习了Dijkstra算法后，给每组布置一个任务，要求对Dijkstra算法进行适当修改，给出能确定图的分支或围长的好算法，并说明为什么是好算法。这些问题略有难度，需要同学们利用集体的智慧解答。学生之间相互交流时没有太大压力，敢于说出自己的真实想法，思维也会更活跃。在你一言我一语的激烈讨论中，不仅成功吸收了新知识，而且在举一反三、触类旁通的过程中，创造性思维也得到了很好的发展。同时团体合作也能增强学生之间的友谊和抵抗挫折的能力，更有利于营造和谐、浓郁的课堂学习氛围。

五、总结

精彩、高效的图论课堂是每个图论老师都梦寐以求的。除了通过各种灵活多样的教学方法吸引学生的注意力、调动学生的积极性外，教师还要多与学生交流，及时了解学生存在的问题，并帮助其解决问题。对于学习能力较差的学生要多给予鼓励，帮助其树立信心，引导他找到正确的学习方向。另外，教师自身也要注意提高教学基本功、知识储备量和课堂驾驭能力。我们相信，只要师生齐心协力、共同努力，一定可以达到良好的教学效果，有效的提高学生的学习成绩。

参考文献

[1]马奎香.图论教学方法研究[J].教育学研究，2012，（10）：37-38.

[2]胡传峰.图论教学方法探析[J].中国科技信息，2012，（12）：235.

[3]王朝瑞.图论[M].北京：北京理工大学出版社，1981.

[4]Bondy J A，Murty U S R.Graph Theory with Applications[M].Elsvier，New York，1976.