车用锂离子动力电池SOC时间序列的BP神经网络预测模型

徐东辉，徐向阳

（1.南昌师范学院数学与计算机科学系，江西 南昌 330046；2.长沙理工大学汽车与机械工程学院，湖南 长沙 410076）

1 引言与研究背景

随着传统燃油车的广泛使用，相应的能源短缺及环境污染等问题随之日益严峻，同时新能源汽车（尤其电动汽车）再次引起世界各国的高度重视。动力电池作为电动汽车的主要动力源，直接影响着电动汽车的行使里程、加速能力及最大爬坡速度等整车性能，因此开发较好的电池管理系统对于提高电动汽车的整体性能具有重大作用。锂离子动力电池与铅酸等电池相比较，具有能量密度高、自放电率低、无记忆效应、使用寿命长及安全性好等优势，成为目前电动汽车的首选动力电池，与其相配套的电池管理系统也成为当前研究热门。

荷电状态（SOC）描述电池剩余电量的数量，类似于传统汽油车的油表。SOC估测是电池管理系统研究的核心之一，也是当前面临的世界性难题。准确地估测SOC对于提高电动汽车的能量效率，有效延长电池循环使用寿命，防止电池过充及过放具有重要意义。目前针对SOC的估算方法开展了很多研究，如：文献［1-2］采用Ah计量法对锂离子动力电池的SOC进行估算；文献［3］通过对开路电压法进行改进，实现了锂离子电池SOC动态估测，估测精度达到了预期效果；刘树林等［4］将分数阶理论应用于锂离子电池等效电路建模中，并且采用了分数阶卡尔曼滤波算法对SOC进行了估计，实验结果显示SOC估计的最大误差小于2%；B.S.Bhangu等［5］在铅酸蓄电池等效电路的基础上建立了状态观测器，并利用Kalman对其状态进行了估测；孙逢春等［6］利用EKF建立了锂电池模糊模型，分别在FUDS、DST等工况下进行了验证，结果显示SOC预测精度达到了较好的要求。以上SOC估测算法中，安时积分法存在库仑效率难以准确测量，SOC初始值难于确定，估测过存中易造成误差累积等问题［7-8］。开路电压法需要通过长时间静置消除极化作用对SOC估测的影响，因此该方法无法在线运行。卡尔曼滤波法适用于电动汽车恶劣环境下的噪声过滤，但估测精度受等效电路模型准确性的影响，且内部参数难以在线实时确定［9-11］。上述算法都属于开环控制模式，且未涉及锂离子动力电池系统非线性混沌特性方面的研究。因此本文针对锂离子动力电池系统高度复杂的非线性特性，提出了SOC时间序列的BP神经网络预测模型。在分析并判别锂离子动力电池系统混沌特性的基础上，采用相空间重构技术恢复锂离子动力电池系统固有的非线性特性，利用BP神经网络对SOC时间序列进行预测，获得SOC预测值。并将SOC预测值代入二阶RC网络模型中计算出电池端电压，将端电压实际测量值与电池端电压计算值作差值比较，利用该偏差对BP神经网络模型进行参数修正，形成有效的闭环控制，达到提高SOC预测精度及实时性目的。

2 锂离子电池动力学系统混沌识别

2.1 相空间重构

假设｛x（ti），i=1，2，…，N｝为车用锂离子电池动力学系统的一维时间序列，相空间重构技术［12-13］可得重构后的相空间可以表示为：

其中：m为嵌入维数，τ为时间延迟，M满足下式条件：

由Packard及Takens定理［14-15］可知找到一合适的嵌入维数与时间延迟后可以从锂离子电池动力学系统的一维时间序列数据中提取和恢复出系统原来的非线性特性，重构的空间与原动力系统保持微分同胚，为锂离子动力电池S OC时间序列预测奠定了坚实的理论基础。

2.2 系统状态混沌性判别

若要将上述的重构相空间时间序列应用于车用锂离子电池的S OC预测中，则必须对锂离子电池动力学系统的时间序列进行混沌判别［16-17］，本文选择小数据量方法对电池动力学系统的时间序列进行混沌判别，具体步骤如下：

（1）估算时间延迟τ和平均周期P，即利用FFT变换获得τ和P；

（2）根据G-P算法估算关联维d，再根据m≥2d+1确定嵌入维数m；

（3）根据τ、m重构｛x（ti），i=1，2，…，N｝时间序列，获得式（1）相空间时间序列；

（4）找相空间中每个点Xi的最近邻点，并限制短暂分离，即；

（5）对每个点Xi，计算其邻点的l个离散时间步后的距离为di（l），表达式如下

（6）对每个l，求出所有lndi（l）的平均y（l），其表达式即为（其中，q为非零di（l）的数目），利用最小二乘法对y（l）进行拟合，得到回归直线，则直线的斜率即为最大Lyapunov指数。

3 S OC时间序列的BP神经网络预测模型建立

3.1 BP神经网络［18-19］

BP神经网络选择2-6-1三层拓扑结构，θl、θj分别为隐层节点l和输出层节点j的阈值，Thl为输入层节点h和隐层节点l之间的连接权值，Tlj为隐层节点l和输出层节点j之间的连接权值，各节点的输入为x，输出为y。

步骤1 初始化。

设输入、输出样本（已归一化）为：

dk，j为第k时刻的实际值，N为样本容量，给各连接 权 ｛Thl｝，｛Tlj｝和 值 ｛θl｝，｛θj｝赋 予 区 间（-0.1，0.1）上的随机值。

步骤2 置k=1，把样本对｛xk，h，dk，j｝提供给网络。

步骤3 计算隐层各节点的输入xl和输出yl，其中l=1，2，…，6。

步骤4 计算输出层各节点的输入xj和输出yj。

步骤5 输出层节点j所收到的总输入变化时单样本点误差的变化率

步骤6 隐层节点l所收到的总输入变化时单样本点误差的变化率

步骤7 修正各连接的权值和阀值

其中，η∈ （0，1）为学习速率。η较大，则算法收敛快，但不稳定，可能出现震荡，η较小则算法收敛缓慢，a的作用恰好与η相反。

步骤8 置k′=k+1，取学习模式对｛xk，h，dk，j｝提供给网络，转至步骤3，直至全部N（N为样本容量）个模式对训练完毕，转至步骤9。

步骤9 重复步骤2至步骤8，直至网络全局误差函数E小于预先设定的一个较小值或学习次数大于预先设定的值，则结束训练。

3.2 S OC时间序列的BP神经网络预测模型

S OC时间序列的BP神经网络预测模型结构如图1所示，本预测模型主要包括相空间重构模块、BP神经网络模块、二阶RC等效电路模块、带遗忘因子的递推最小二乘辨识模型等组成，主要预测步骤如下：

步骤1：利用温度、电流及电压等传感器实时在线测取电池温度T（k）、电流I（k）及端电压U（k）等数据；

步骤2：利用相空间重构技术对采集到的温度、电流及电压等数据进行重构，恢复锂离子动力电池系统固有的非线性特性；

步骤3：将重构后得到的数据作为BP神经网络模块的输入量进行预测，得到锂离子动力电池系统S OC时间序列的预测值；

步骤4：将电流I（k）及S OC时间序列的预测值作为二阶RC等效电路模型输入变量，通过公式计算得到端电压UL（k）的计算值；

步骤5：根据BP神经网络全局误差函数式（15）判断系统全局误差，若大于预先设定的值或学习次数小于预先设定的值，则修正BP神经网络各连接的权值和阀值，并且重复执行步骤3至步骤5，反之则结束学习，得到S OC的最终预测值。

图中，T（k）为电池温度、I（k）为电流、U（k）为端电压、S OC（k）为BP神经网络预测值、UL（k）为端电压的计算值、e（k）=U（k）-UL（k）为端电压的测量值与计算值的差。

车用动力电池等效电路模型主要有内阻、Thevenin、PNGV、Massimo Ceraolo等模型［20-21］。本文采用基于RC电路与Thevenin模型的二阶RC等效电路模型，二阶RC等效电路模型充分考虑了电流、温度、充放电等对电池内阻的影响，能较准确地模拟电池的动、静态特性，具有精度高，结构简单，计算复杂度低，参数易辨识实现等优点。目前该模型普遍应用于动力电池建模、仿真等领域，二阶RC等效电路模型结构如图2所示。

二阶RC等效电路模型表达式：

由上述式（16）及式（17）可知，若要准确在线的计算出端电压UL值，则必须对二阶RC等效电路模型中 的R0、R1、C1、R2、C2等 值 进 行 实 时 在 线 辨识。目前参数辨识领域的算法主要包括最小二乘法、预报误差法、极大似然法等，但以上算法大都很难实现实时在线辨识，为此本文选择带遗忘因子的递推最小二乘法对二阶RC等效电路模型参数实现实时在线辨识。

为了将带遗忘因子的递推最小二乘法成功应用于二阶RC等效电路模型参数辨识中，必须将二阶RC等效电路模型转化为最小二乘法基本结构形式。

对式（16）进行 Laplace变换，定义EL（s）=为电路阻抗，则可得：

式中：τ1=R1C1，τ2=R2C2。

根据双线性变换原理对上式进行离散化处理，可得离散传递函数为：

式中：α1，α2，β0，β1，β2为待定系数。

则由式（19）可得离散化后的差分方程为：

令：

则可得最小二乘法形式为：

其中T为采样周期。

递推最小二乘法是在最小二乘法基础上发展起来的，它是在系统运行过程中，每测量一组新数据，通过递推公式修正前一时刻的预测值来获得当前时刻的参数值估计值，直到参数估计值逐渐逼近满意的精度为止。递推最小二乘法易出现“数据饱和”现象，遗忘因子递推最小二乘法是在递推最小二乘法算法的基础上进行改进而得到的，通过引入一个遗忘因子λ（λ的取值范围为0.95～0.99）减弱旧数据的作用而增强新数据的作用，有效克服“数据饱和”现象。改进后的评价函数为：

带遗忘因子的递推最小二乘法算法的递推公式如下：

图2中，UL为端电压；UOC为开路电压；R0为欧姆内阻；R1、C1为电化学极化电阻和极化电容，R2、C2为浓度差极化电阻和极化电容。

4 S OC时间序列的BP神经网络预测仿真

4.1 试验数据采集

本文研究对象选择100Ah的磷酸铁锂离子动力电池，试验工况选择DST工况。上位机为PC机，运行BTS-600软件及SQL Sever数据库软件。下位机选用美国Arbin公司生产的BT2000电池测试系统，其电压的测量精度为±0.01%，电流的测量精度为±0.02%。在部分实验中采用美国Agilent公司生产的34410A型6 1／2位数字万用表作为电压辅助测量工具，提高电压测量精度。DS18B20传感器为环境温度采集设备，精度为±0.5°C。每次试验共采集电压、电流及温度等600组试验数据，共进行5次试验，获得5×600组试验数据。S OC与OCV的曲线关系由下式拟合出：

4.2 嵌入维数和时间延迟的确定OCV-S OC

本文利用上述小数据量方法计算得最大Lyapunov指数为0.016 2，稍大于0，表明锂离子电池动力学系统的时间序列具有混沌特性，因此可对车用锂离子电池S OC做短期预测。若要对上述试验采集到的一维数据进行相空间重构首先必须确定嵌入维数和时间延迟，为此本文采用C-C法确定嵌入维数和时间延迟，具体步骤如下：

（1）计算给定时间序列的标准差σ；

（2）通过matlab编程序计算

其 中： 时 间 变 量t≤ 200，S（m，rj，t）=max｛S（m，rj，t）｝-min｛S（m，rj，t）｝

（3）在 matlab 中 对 上 述 2）中ΔS（m，t）、（t）、Scor（t）进行作图，① 在ΔS（m，t）与t（0≤t≤200）曲线图中ΔS（m，t）的第一个极小值处t对应τd=tτs（τs为时间序列的采样间隔）；② 在与t（0≤t≤200）曲线图中的第一个极小值处t对应τd=tτs；③ 在Scor（t）与t（0≤t≤200）曲线图中Scor（t）的最小值处t对应τw=tτs。

根据上述步骤计算的τ=3，τw=21，通过τw=（m-1）τ计算的嵌入维数m=8，因此最后确定了锂离子电池动力学系统时间序列的τ=3、m=8，并利用此结果对车用锂离子动力电池S OC时间序列进行相空间重构。

4.3 SOC时间序列的BP神经网络训练与预测

BP神经网络［20］选择8-6-1结构，学习步长取1500，允许误差为0.01，对采集的5×600组实验数据进行重构，得到25×600组数据，随机选取20×600组为BP神经网络预测模型的训练样本，另5×600组数据为检验样本。RBF神经网络选择8-6-1结构，学习步长取1 500，允许误差为0.01，隐含层选择高斯函数，为验证相空间重构技术能提高BP神经网络预测精度，本文从采集到的5×600组原始实验数据中随机选取4×600组为RBF神经网络训练样本，剩余的1×600组为检验样本。二阶RC等效电路模型参数辨识结果如表1所示，SOC时间序列BP神经网络预测值与标定值的比较如图3所示，BP神经网络预测值与标定值的比较如图4所示，预测误差比较如图5所示。

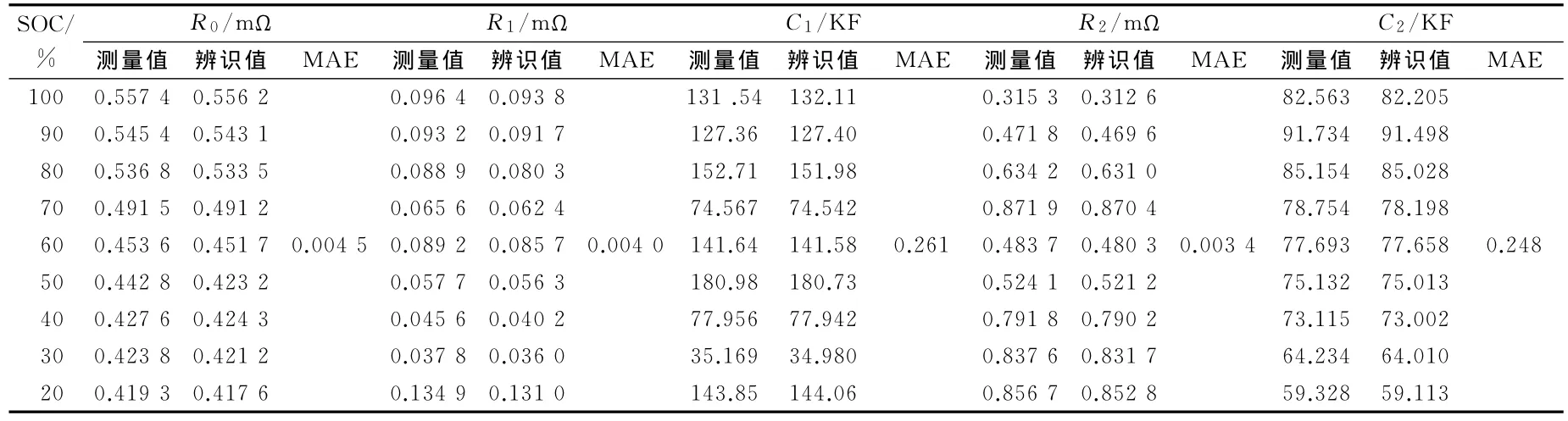
表1 二阶RC等效电路模型参数辨识结果

4.4 误差分析与比较

通过图2～4及表1～2的误差分析与比较表明相空间重构技术能够恢复锂离子动力电池原有的多维非线性特性，从多维状态空间方面扩大预测模型的训练样本量，提高BP神经网络预测模型的预测精确度。带遗忘因子的递推最小二乘法能有效在线辨识二阶RC网络模型的参数，克服了递推最小二乘法易出现“数据饱和”现象。同时表明由二阶RC网络模型、BP神经网络及带遗忘因子的递推最小二乘法构成的闭环控制系可以实现SOC时间序列实时在线预测，达到了较满意的精度。

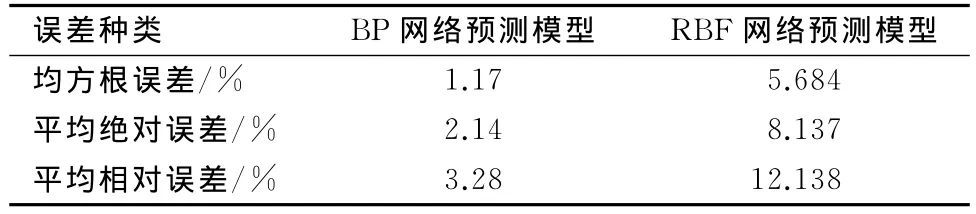
表2 误差分析与比较

5 结论

（1）针对车用锂离子动力电池系统高度复杂的非线性特性，SOC难于实时在线获取的难题，提出了SOC时间序列的BP神经网络预测模型；利用二阶RC网络模型、带遗忘因子的递推最小二乘法与BP神经网络构成闭环控制系统，实现了SOC实时在线获取。

（2）对锂离子电池动力学系统进行了混沌特性判别，并利用相空间重构技术恢复了锂离子电池动力系统原有的多维非线性特性，同时增加了BP神经网络训练样本空间。

（3）仿真结果显示本预测模型具有较高的精确度、较强的实时性，与RBF神经网络模型比较，平均相对误差提高了近8个百分点。表明了相空间重构技术可以有效地恢复系统原有的多维非线性特性，有利于提高BP神经网络预测精度，由二阶RC网络模型与BP神经网络构成的闭环控制系统具有较高的实时性，对于实际工程应用具有较好的指导意义。