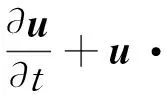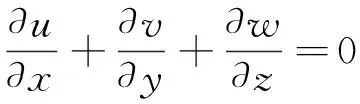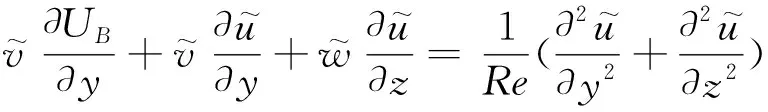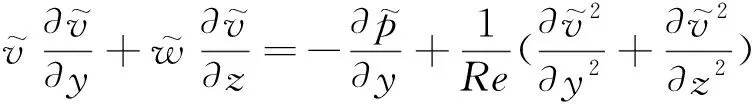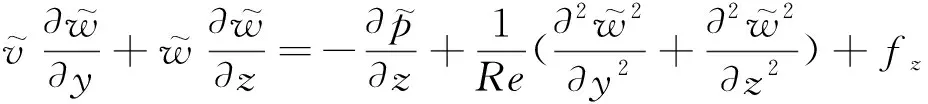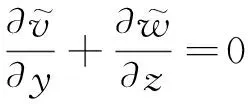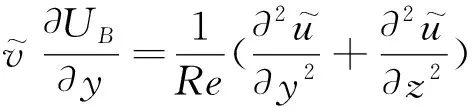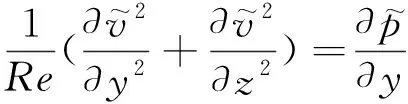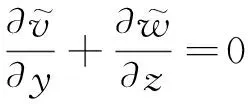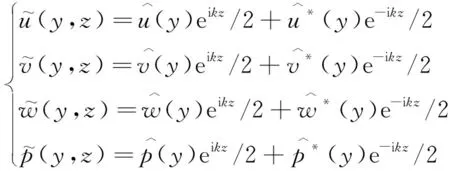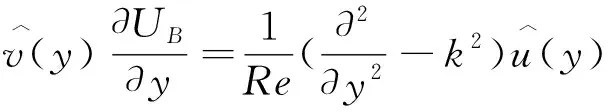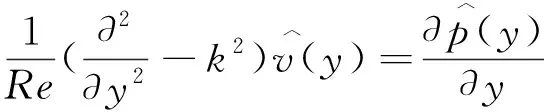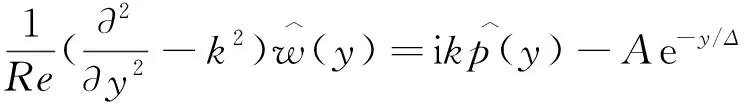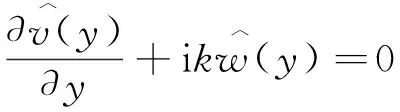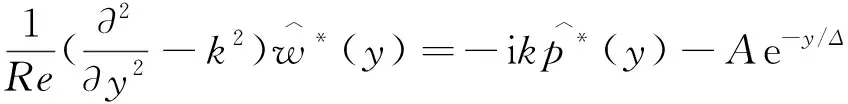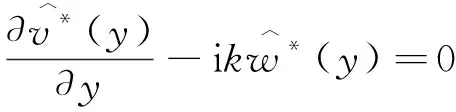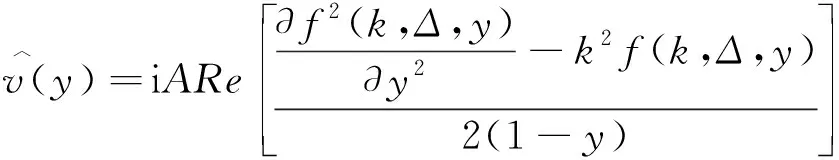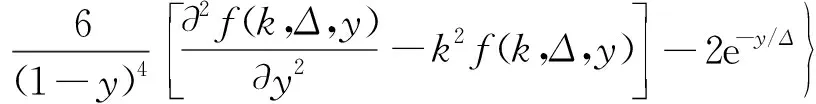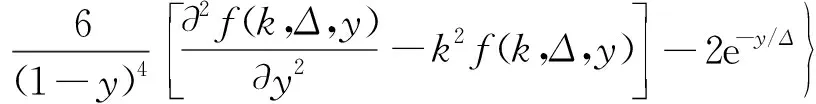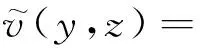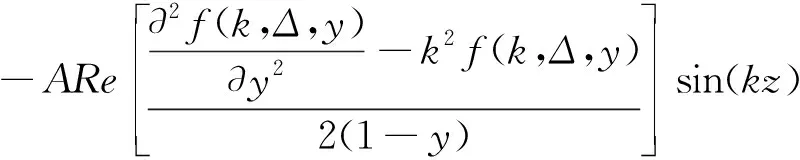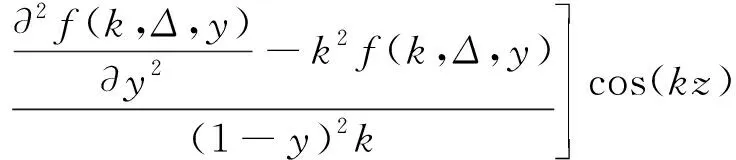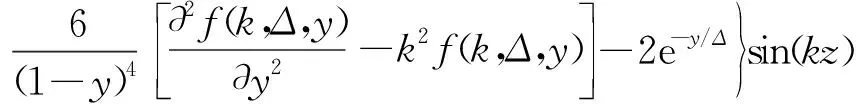电磁力作用下槽道流速度响应的放大机理
张成龙, 张 辉,2,*, 江代文
(1. 南京理工大学 瞬态物理国家重点实验室, 南京 210094; 2. 帝国理工学院 数学系, 伦敦 SW7 2AZ, 英国)
0 引 言
飞行器、舰船等航行体在运动时,黏性流体在其表面形成的边界层可产生较大的阻力、振动和噪声,严重时会导致航行体失稳。为了减少此类情况的发生,对边界层加以适当的控制,通过改变其结构,从而达到减阻、减振、降噪的效果[1-4]。目前的主动控制方法虽能取得显著的控制效果,但输入的能量较大,甚至比减阻节约的能量高一个数量级以上,因此减少输入能量、提高控制效率成为制约主动流动控制发展的瓶颈问题。
电磁力流动控制方法作为主动流动控制方法之一,有响应速度快、控制效果好、灵活性强等优点,在层流和湍流的流动控制中都有广泛应用[5-6]。英国学者Gailitis最早利用电磁力进行流动控制,将电磁激活板置入弱电解质溶液中,通电后产生的电磁力可以改变边界层结构。随着电磁流动控制的发展,其控制效率问题逐渐受到越来越多的关注。其中槽道流动作为一种典型流动,由于其流向和展向满足周期性边界条件,从而在计算量不大的情况下即可进行层流和湍流的直接数值模拟,但却也是因此不能直接利用此方法进行转捩流动的研究。Berger[7]等对槽道湍流的电磁力控制进行直接数值模拟,讨论了电磁力的控制效率问题。他将控制效率定义为:减阻节约的能量与施加电磁力所使用的能量之比。研究发现,对较低雷诺数下的槽道湍流施加展向电磁力,减阻率可达到40%,但是所需电磁力的能量比减阻节省的能量大一个数量级以上。当雷诺数增加时,控制效率进一步减小。O’Sullivan[8]等在类似的研究中发现,当施加的电磁力很小时,很难对湍流流场产生实质性的影响。而逐渐增大施加的电磁力,产生电磁力输入的能量始终比减阻节约的能量大。后来,Shatrov[9]等同样利用直接数值模拟,用时变电磁力和恒定电磁力分别对槽道湍流进行控制。结果表明,研究的所有参数组合中,输入能量均大于减阻节约的能量。Gadel-Hak[10]利用了闭环反馈控制方法,但并未显著提高槽道湍流的电磁力控制效率。Rogers[11]、Sankar[12]等对电磁力控制翼型绕流分离的增升减阻效率进行研究,分析了电磁力控制过程及不同工况条件下的电磁力控制效率。陈耀慧[13]等数值研究了翼型绕流电磁力控制过程,发现电磁力控制能量的损耗主要体现在流体动能上。Chen[14]等比较了全包覆和局部包覆的电磁力控制方法,结果表明,在特殊位置施加局部电磁力控制流动的效果与全包覆电磁力的控制效果相当,但输入能量仍大于减阻节约的能量。
综上,目前的电磁力控制方法虽能取得很好的控制效果,但控制效率很低。本文作者也曾对电磁力的优化控制进行过相关研究[5-6],但仅通过参数优化、局部作用、反馈控制等方法,收效甚微,其根源在于输入的能量较大,即施加较大的电磁力才能在流场中诱导出足够大的响应。因此,若能以较小的电磁力便可诱导出大的响应,这将为大幅提高控制效率提供可能。
本文以层流槽道流动作为研究对象,在槽道的下壁面施加沿展向余弦分布的展向电磁力,推导了线性条件下流向响应速度的解析解,并通过直接数值模拟对非线性条件下的响应进行了计算。结合解析解和数值解,揭示了流场中速度响应的放大机制,讨论了电磁力和流场参数对响应放大效果的影响。
1 理论模型
以弱电解质溶液在槽道中的层流流动为研究对象,模型如图1所示。直角坐标系原点位于下壁面,其中x、y、z分别代表流向、法向和展向。槽道在这三个方向的尺寸为Lx×Ly×Lz=(4π/3)×2×(2π/3)。
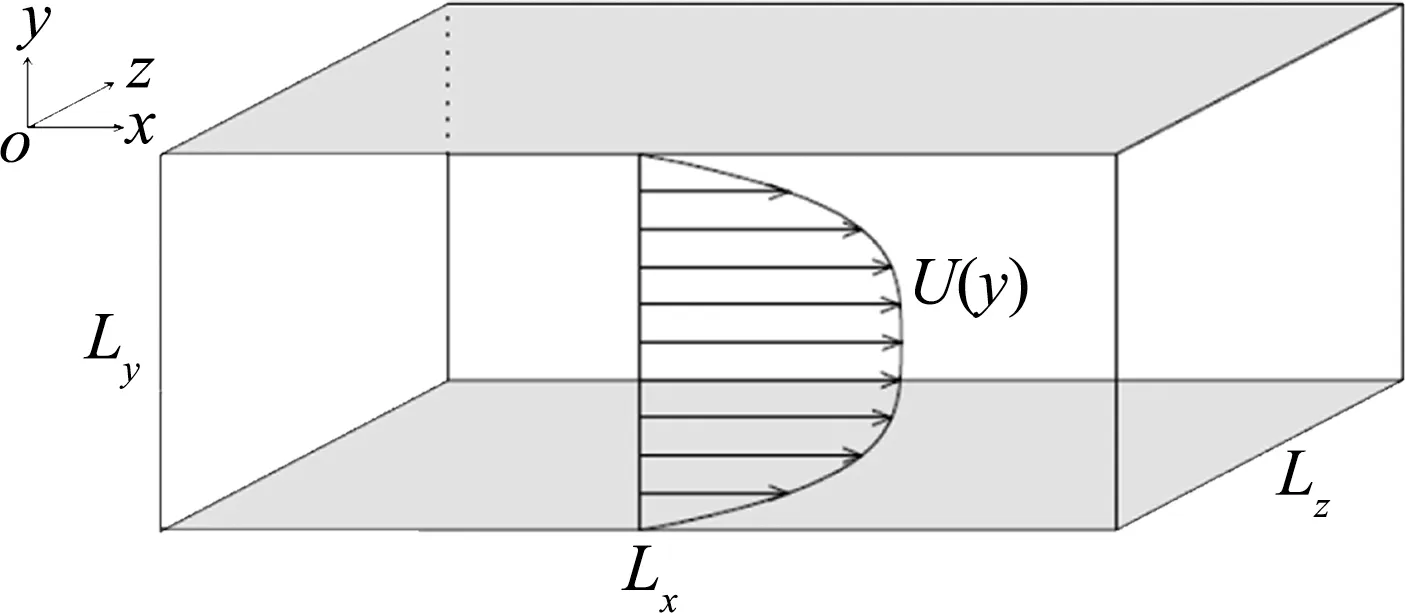
图1 槽道模型示意图Fig.1 Diagrammatic sketch of channel flow
对此不可压缩三维槽道流,将电磁力作为源项,无量纲化N-S方程为:

(1)
·u=0
(2)

f=(0,0,fz)
(3)
fz=Ae-y/Δcos(kz)
(4)

1.1 线性条件下的解析解
将式(1)、式(2)写成直角坐标系下的形式,有

(5)

(6)

(7)

(8)

(9)
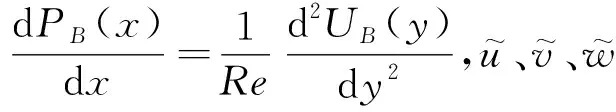
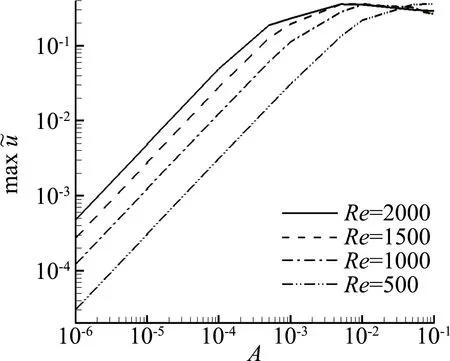
考虑到槽道流的特点,式(1)和式(2),沿流向和展向满足周期性边界条件,法向满足壁面无滑移边界条件[6]。初始条件为基本流UB(y)=1-(1-y)2=2y-y2,(0 当电磁力振幅0 (10) (11) (12) 2e-y/Δ}sin(kz) (13) 随着电磁力的增大,流场的响应逐渐进入非线性范围,因此需要通过数值计算去求解。本文采用直接数值模拟,对方程(1)和(2)利用Fourier-Chebyshev谱方法进行空间离散。时间项采用三阶精度的半隐式向后差分格式求解。线性项和压力项,通过影响矩阵法和Chebyshev-tau方法联立求解,以消除残余散度。非线性项,利用3/2规则消除混淆误差。槽道沿流向和展向均采用均匀网格周期性边界条件,沿法向为非均匀网格壁面无滑移条件[6]。文中使用的上述算法基于槽道湍流的算例验证已在文献[6]中详细讨论,层流时的速度响应将在下文中与解析解结果进行对比。计算过程中流向流量保持不变,并选取雷诺数Re=500~2000的算例进行研究。 (a) 数值解 (a) A=1×10-5 (a) Kz=1 图5 最大响应速度随渗透深度和波数的变化Fig.5 Variations of the response with effective penetration and wave number 图6 流向最大响应速度放大倍数随波数和振幅的变化Fig.6 Variations of the amplification along the streamwise direction with wave number and amplitude 图7 流向最大响应速度随波数和振幅的变化Fig.7 Variations of the response with wave number and amplitude 图8 流向最大响应速度放大倍数随渗透深度和振幅的变化Fig.8 Variations of the amplification along the streamwise direction with effective penetration and amplitude 图9 流向最大响应速度随渗透深度和振幅的变化Fig.9 Variations of the response with effective penetration and amplitude 图10 流向最大响应速度放大倍数随雷诺数和振幅的变化Fig.10 Variations of the amplification along the streamwise direction with Reynolds number and amplitude 图11 流向最大响应速度随雷诺数和振幅的变化Fig.11 Variations of the response with Reynolds number and amplitude 本文以层流槽道流动作为研究对象,在槽道的下壁面施加沿展向分布的电磁力,推导了线性条件下流向响应速度的解析解,并通过直接数值模拟对非线性条件下的响应进行了计算。结果表明: 1) 当振幅较小时(A≤1×10-4),速度响应处于线性范围,其放大倍数与Re2成正比;随着Δ的增大,先迅速增大后缓慢减小;随着展向波数Kz的增大单调减小。此时最大响应的放大倍数在102~ 103量级。 2)随着振幅的增大,放大倍数进入非线性范围,其值逐渐减小,但速度响应值先增大后减小。在振幅处于10-3~10-2量级时,速度响应可达到最大值超过0.2,此时的放大倍数在102量级。 利用流场的放大效果与Re2的相关性,将电磁力的响应先进行放大,再用来控制流场的流动,为目前的主动流动控制理论和技术提供了新的方法。本文基于大响应的研究是实现高效流动控制的重要环节。 附 录 线性条件下解析解的详细推导如下。 对本文中不可压缩三维槽道流,将电磁力作为源项,其无量纲化N-S方程为: (1) ·u=0 (2) f=(0,0,fz) (3) fz=Ae-y/Δcos(kz) (4) 将方程(1)、(2)写成直角坐标系下的形式,有 (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) 在槽道流中沿z方向满足周期性条件,因此方程组解的形式如下: (18) 式(4)中的电磁力可写为: fz=Ae-y/Δcos(kz) =Ae-y/Δeikz/2+Ae-y/Δe-ikz/2 (19) 将式(18)、式(19)的等号右端第一项代入式(14)~式(17)可得: (20) (21) (22) (23) 同样,将第二项代入式(14)~式(17)可得: (24) (25) (26) (27) 求解方程组,可得 (28) (29) (30) (31) (32) (33) (34) (35)
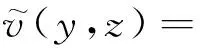
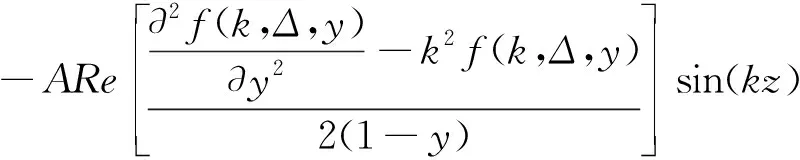


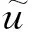
1.2 数值解
2 结果与讨论
2.1 流向响应速度的算例验证



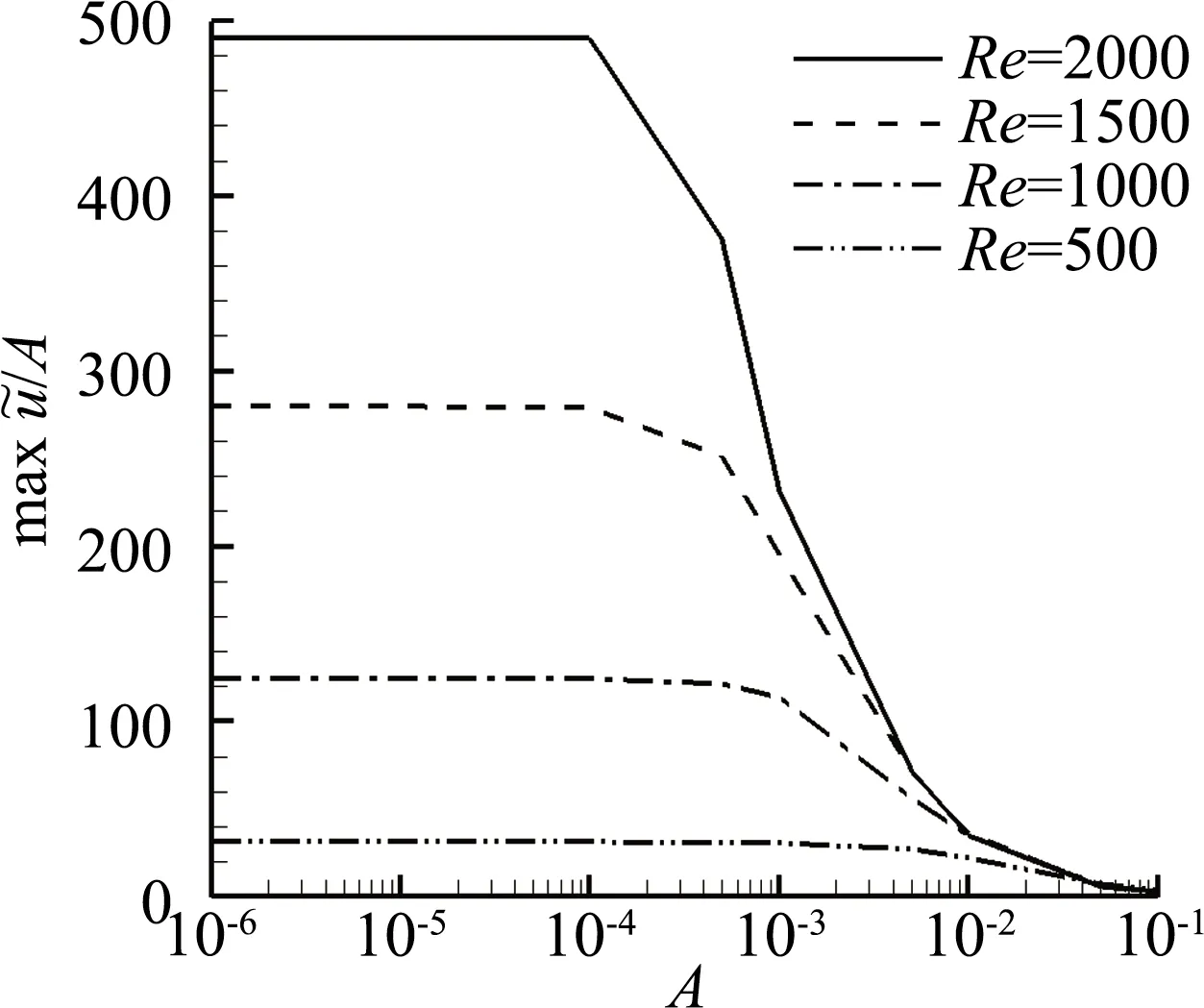
2.2 流向速度响应随电磁力和流场参数的变化










3 结 论