高压捕获翼构型跨声速流动特性初步研究

王浩祥, 李广利,*, 徐应洲, 崔 凯

(1. 中国科学院力学研究所 高温气动国家重点实验室, 北京 100190； 2.中国科学院大学 工程科学学院, 北京 100049)

0 引 言

高超声速飞机因可实现快速有效运输和全球快速打击，而成为目前国内外研究的热点问题[1]。早在1986年美国发展的NASP计划中，X-30空天飞机除了作为新一代航天运输工具外，也描述了其作为高超声速飞机应用的美好前景。近期继洛马公司提出SR-72之后，波音公司连续公布了军用和民用两种高超声速飞机概念方案和研制计划[2]。此外，Lobbia等[3]综合考虑气动、动力、质量和容积等因素，通过多学科/多目标优化提出了一种高超声速飞机概念构型，欧洲联合俄罗斯、澳大利亚和巴西等国，以高超声速民用飞机为方向，开展了Hexafly-Int研究计划[4]。国内近期也开展了相关研究，其中文献[5]和文献[6]分别提出了双旁侧进气和背部进气方式的高超声速飞机构型方案。综合来看，关于高超声速飞机的研究仍处于概念探索阶段。

从气动构型设计角度而言，高超声速飞机应具有高升阻比特性以增加其巡航距离，同时应具有较大的容积以容纳乘客、货物和燃料等，此外，也应具有较大的升力系数以提供更好的升重平衡，从而可有效缓解结构减重问题。然而，在高超声速飞行中，激波阻力和摩擦阻力急剧增大，导致气动性能急剧下降，并且实际设计中升阻比与容积率、升阻比与升力系数之间均存在强烈的矛盾关系，因此同时满足上述三种需求十分困难[7]。针对上述问题，文献[8]提出了一种全新的高压捕获翼气动布局概念，对于有大容积需求的高速飞行器，通过在其上方添加高压捕获翼，可以有效利用机体压缩激波所产生的高压区，从而可大幅提高升力和升阻比。文献[9]中的研究结果充分验证了该构型在高超条件下的高升阻比、高容积率和高升力系数的“三高”特性。依据现有的研究结果，高压捕获翼构型将可成为一种极具应用前景的高超声速飞机布局概念。

关于高压捕获翼构型的前期研究主要集中于高超声速飞行条件[10-12]，而对于水平起降的高超声速飞机而言，不仅要关注巡航状态下的高速性能，还需关注飞行过程中其他速域的气动性能，尤其是跨声速飞行条件下[13-16]，在飞行器局部区域将会产生激波，导致飞行器阻力急剧增加，并且激波与壁面边界层发生相互作用，使边界层内部存在较大的逆压梯度。当激波强度足够强时将引起当地边界层的分离和再附，或者完全破坏原来的流动，产生大范围的分离区，导致流动分离一直延续到飞行器尾部，严重影响飞行器的气动性能。

根据高压捕获翼构型的设计原理[10]，捕获翼应置于机体上方并与机体保持合理间距。同时，为了保证机体前部的足够压缩以及反射激波掠过机体后部，机体构型一般采用先压缩后扩张的设计方式，这样机体和捕获翼之间可近似为一个先收缩后扩张的内流道。在跨声速条件下，机体附近和捕获翼附近的绕流流场将完全耦合，激波与分离区的相互作用使得机体与捕获翼之间形成的开放通道内的流场结构变得更加复杂，所出现的气动干扰可能会对飞行器的升阻特性及稳定特性均产生十分显著的影响。因此，研究和分析该类新构型跨声速条件下的气动性能和流场结构十分有必要。

基于上述背景，本着由简至繁的原则，本文基于一种简化的高压捕获翼原理构型，以马赫数0.92、0°攻角为条件，利用CFD数值模拟开展了初步研究，并对结果进行了分析。其中，重点探索典型跨声速条件下机体和高压捕获翼间的强相互干扰区的流场结构及其对壁面压力的影响，以期为后续的宽速域构型设计和多点优化等研究工作奠定基础。

1 高压捕获翼原理和计算模型简介

高压捕获翼在高速流动条件下的设计原理如图1所示[12]，图中区域①为自由来流，高速来流经过机体上表面压缩，产生第一道斜激波S1，在激波S1后压力增加，流动方向与机体上表面平行，之后在捕获翼的压缩下形成第二道激波S2，使压力获得进一步提升，随来流继续前进，在机体尾部产生膨胀波，经前马赫线(FML)后压力逐渐减小，然后流向下游，由于捕获翼平行于来流，区域⑤的压力基本与自由来流压力相等。由上述描述可知区域③经两次压缩，捕获翼下表面的压力明显高于上表面，因此捕获翼可为飞行器提供较大的升力。当采用薄翼设计时，其阻力增加较小，飞行器的升阻比也可获得大幅提升。

为突出重点，本文依据上述设计原理采用了一种简化外形，使用一个圆锥-圆台组合体作为概念机体，在其上方设置高压捕获翼，其外形为具有一定厚度的平板，前缘进行钝化。外形主要参数如下：以机体长度为参考量，无量纲化的捕获翼相对长度为0.431；相对宽度为0.333；相对厚度为2.667×10-3。捕获翼与机体间的相对位置依据文献[10]中的捕获翼位置设计方法给定。按上述方法生成的计算模型如图2所示。

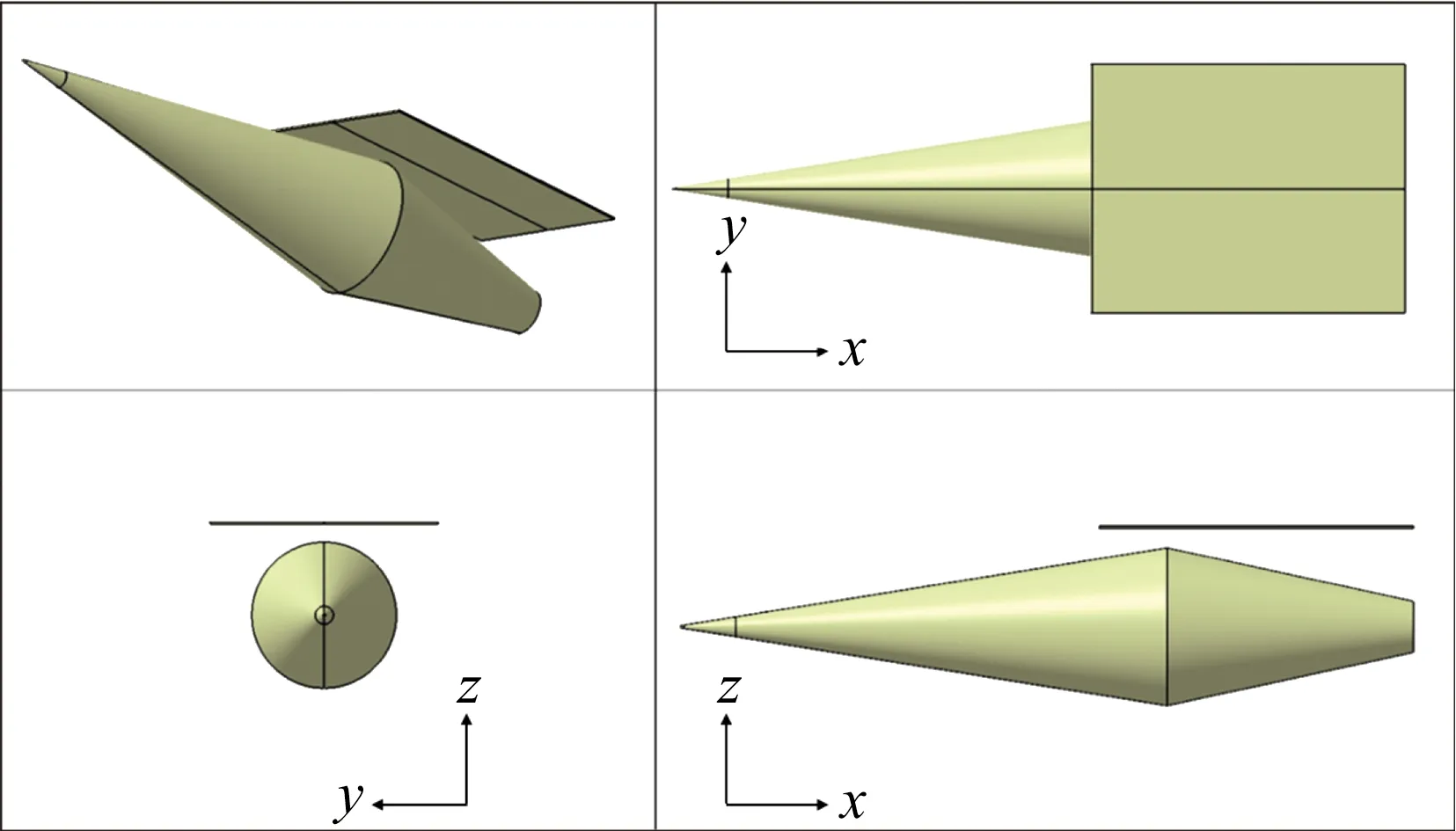
图2 构型三维视图和三视图Fig.2 Three-dimensional and three view of the configuration

为验证该构型的效果，在设计条件下对其流场进行了计算，条件如下：来流马赫数为6.0，单位雷诺数为2.258×106/m，飞行攻角为0°。图3给出了该构型在设计条件下的物面和纵向对称面压力云图。从图中可以看到，机体压缩产生的激波打在捕获翼前缘附近，并且反射激波刚好掠过机体最高点，符合高压捕获翼构型的基本设计原则。

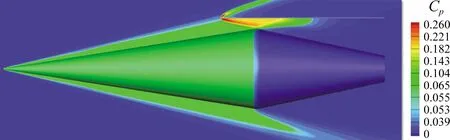
图3 纵向对称面的压力分布云图Fig.3 Pressure contours in the symmetrical plane

2 CFD可靠性验证

本文数值模拟基于三维可压缩流动N-S方程，数值方法采用TVD(Total Variation Diminishing)格式，时间推进选用隐式格式，湍流模型为SST模型。首先以ONERA M6 机翼标模[17-18]对本文的CFD方法进行验证。计算条件为来流马赫数0.84，雷诺数为7.12×107/m，飞行攻角3.06°。为保证计算结果的可比性，计算网格选用NASA公布的结构网格，如图4所示，总网格量约29.5万，网格节点约30.5万，物面法向第一层网格厚度为机翼翼展长度的10-5量级。

图4 ONERA M6 机翼网格示意图Fig.4 Illustration of computational grid for ONERA M6 wing

图5给出了沿翼展方向不同截面的翼型表面压力分布，图中三组数据分别为NASA实验结果、NASA数值结果和本文计算结果。从图中可以看出，本文数值结果与NASA数值结果和实验结果均符合较好，说明本文数值方法具有较高的可信度。

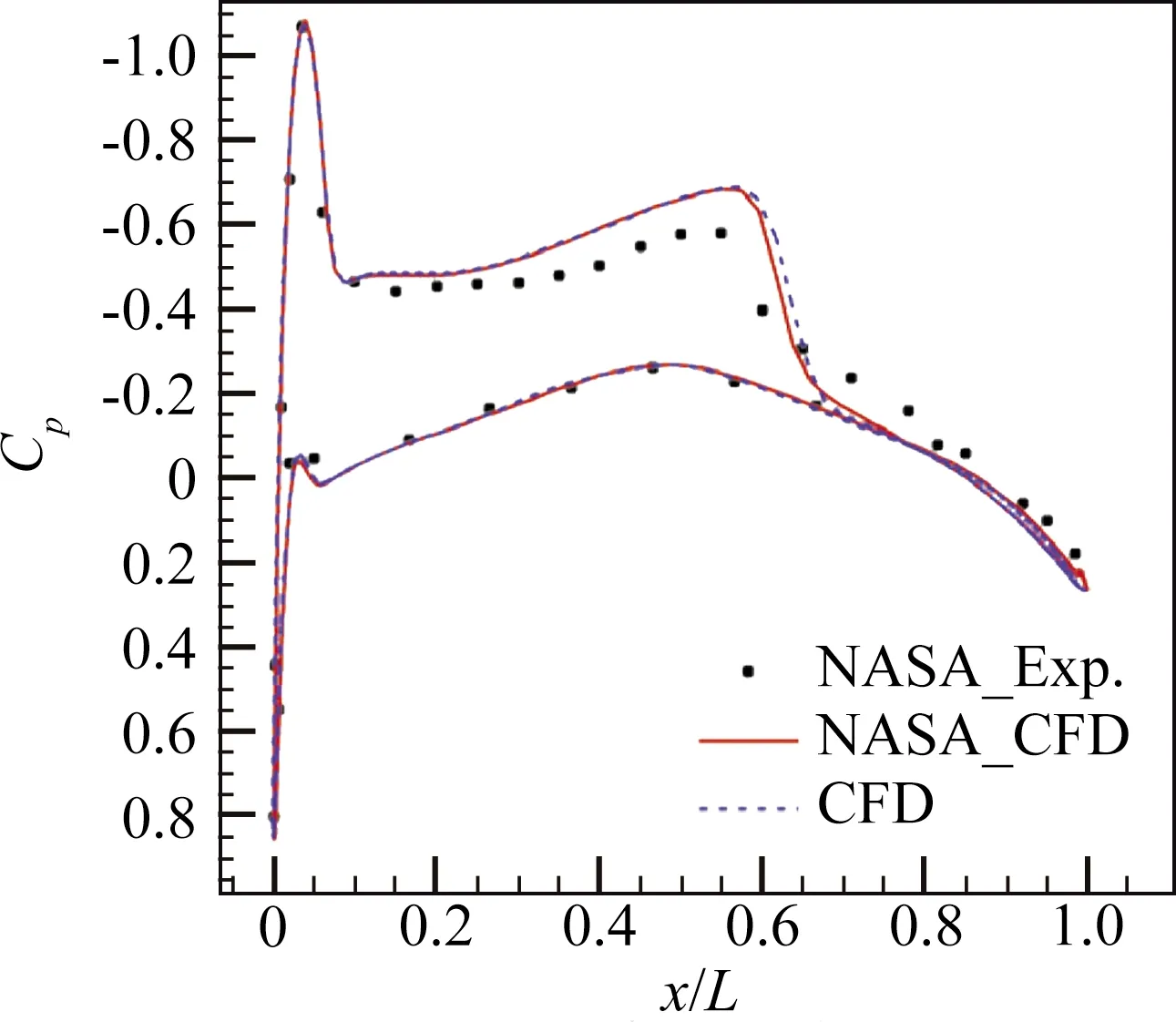
(a) y/b=0.20

3 计算结果及分析

采用上述数值方法分别对圆锥-圆台体和圆锥-圆台体组合高压捕获翼构型进行了流场结构分析，两组构型均采用结构网格对计算区域进行离散，近壁面网格进行加密，总网格量约为2900万。图6给出了后者的结构网格示意图。计算条件为：马赫数0.92，单位雷诺数1.334×107/m，攻角为0°。

图6 结构网格示意图Fig.6 Illustration of computational grid

为保证计算准确性，选取了不同的网格尺度进行计算。参考标模计算参数，以整机长度为参考量，近物面首层网格尺度分别采用1×10-5和1×10-6。结果表明，升力和阻力系数的变化均在3%以内。此外，图7分别给出了两种网格条件下的马赫数云图，可以看到流场结构趋于一致，因此计算结果可信。后续计算均采用1×10-5网格尺度。

为进行对比，同时对不加捕获翼的圆锥-圆台体(机体)绕流流场进行了计算，为保证可比性，两个算例的网格分布和近物面第一层网格尺度等参数基本保持一致。计算结果如图8所示。从图中可以看出，来流经锥体压缩后不断加速，到达圆锥和圆台体转折处流体达到超声速，并产生一道弱激波。在尾部收缩段(圆台部分)出现了大面积的流动分离，由于分离区的存在，波后亚声速气流继续被压缩，并产生了二次激波，形成了类似于收缩管道的流动结构，随气流马赫数的不断变化，出现了“超声速舌”现象[16]。

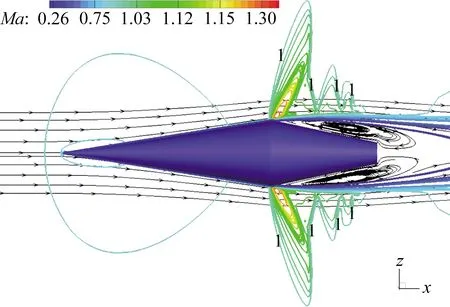
图8 圆锥-圆台体对称面上的流场结构Fig.8 Flow field structure on the symmetrical plane of referred configuration

图9给出了增加高压捕获翼后的对称面流场结构。构型上方添加高压捕获翼后，在其上表面前半部分达到超声速，并产生了一道激波，该激波与上壁面边界层发生相互作用，但未引起流动分离；圆台上方受高压捕获翼影响，产生了较下方区域更大范围的流动分离区；对于高压捕获翼和圆锥-圆台体中间区域，在二者强烈的相互干扰作用下，流场变得更为复杂。

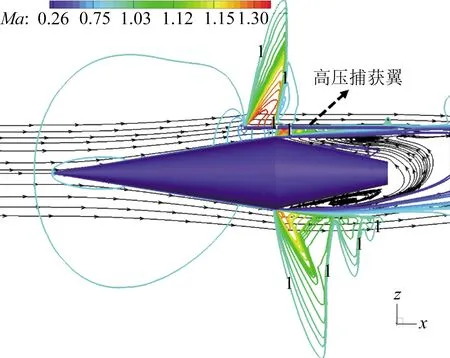
图9 圆锥-圆台体组合高压捕获翼对称面上的流场结构Fig.9 Flow field structure on the symmetrical plane of the HCW configuration

3.1 高压捕获翼对流场结构的影响

增加高压捕获翼后，对构型流场结构的影响主要体现在其附近区域。图10给出了三组不同展向截面高压捕获翼附近的马赫数分布。可以看出，由于捕获翼的影响，机体尾部分离区明显增大，由此导致高压捕获翼和机体之间一直呈现出等效的收缩形状。在跨声速来流条件下，收缩通道内出现了激波串现象，进而形成了多个超声速区和亚声速区。随展向位置增加，尽管等效通道的宽度增大，但仍一直保持收缩状态。

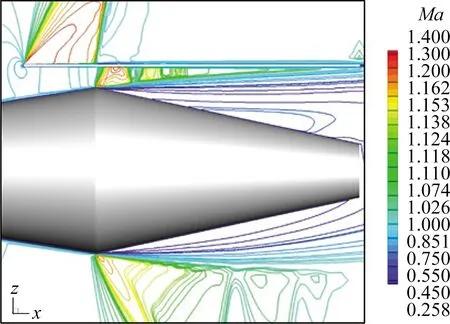
(a) y/L=0

图11为x/L=0.69(右上角给出了位置示意图)截面上的马赫数分布。从图中可以发现，机体下侧的流场基本未受到高压捕获翼的影响，即与二维轴对称流场基本一致。而上表面受高压捕获翼影响，呈现出明显的三维特征。此外，由于在对称面附近压缩最强，所以对应的马赫数数值相对较高。随展向位置不断增加，高压捕获翼的影响逐渐减弱，马赫数分布也逐渐趋于均匀，直至与二维轴对称流场基本一致。图12给出了z/L=0.123截面(靠近捕获翼下表面的纵向位置)上不同展向位置的马赫数分布，其中横坐标的位置范围为捕获翼前缘到尾缘。可以看出在捕获翼与机体之间的通道内均出现了激波串现象，而且随展向位置增加，通道的等效宽度逐渐增加，导致激波强度逐渐减弱，同时激波位置也逐渐后移。

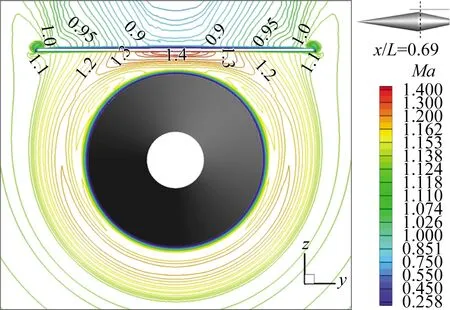
图11 x/L=0.69截面上的马赫数分布图Fig.11 Mach number distribution on the cross-section at x/L=0.69

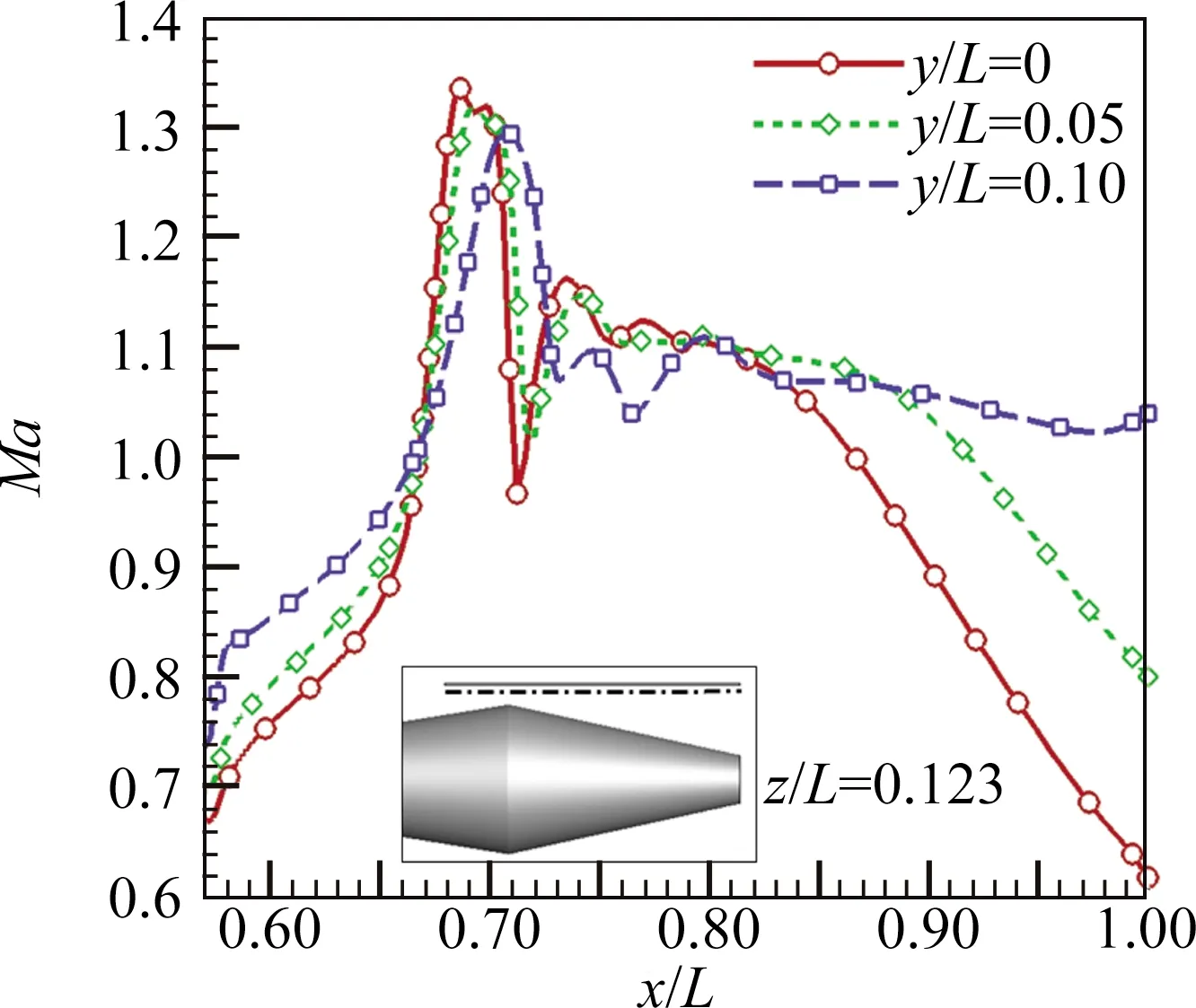
图12 z/L=0.123截面上不同展向位置的马赫数分布Fig.12 Curves of Mach number variation at different positions at y direction (z/L=0.123)

3.2 壁面压力分布特性

图13给出了不同展向位置截面中高压捕获翼上下表面的压力分布曲线比较。由图中可见，捕获翼上表面的压力分布与跨声速机翼类似，受激波影响，在前半部分压力急剧增加，激波之后为亚声速区域，并且流动趋于均匀，压力基本保持不变。随展向位置增加，由于翼边缘三维效应的影响，激波强度逐渐减弱，导致上表面对应的最大压力相应减小。在捕获翼下表面由于压缩影响，马赫数增加，因此压力逐渐减小，之后受激波串影响，压力呈现明显的波动。在过激波串以后，马赫数缓慢减小，因此壁面压力缓慢增加。并且随展向位置增加，最小压力值增大、最大压力值减小，且对应位置后移。

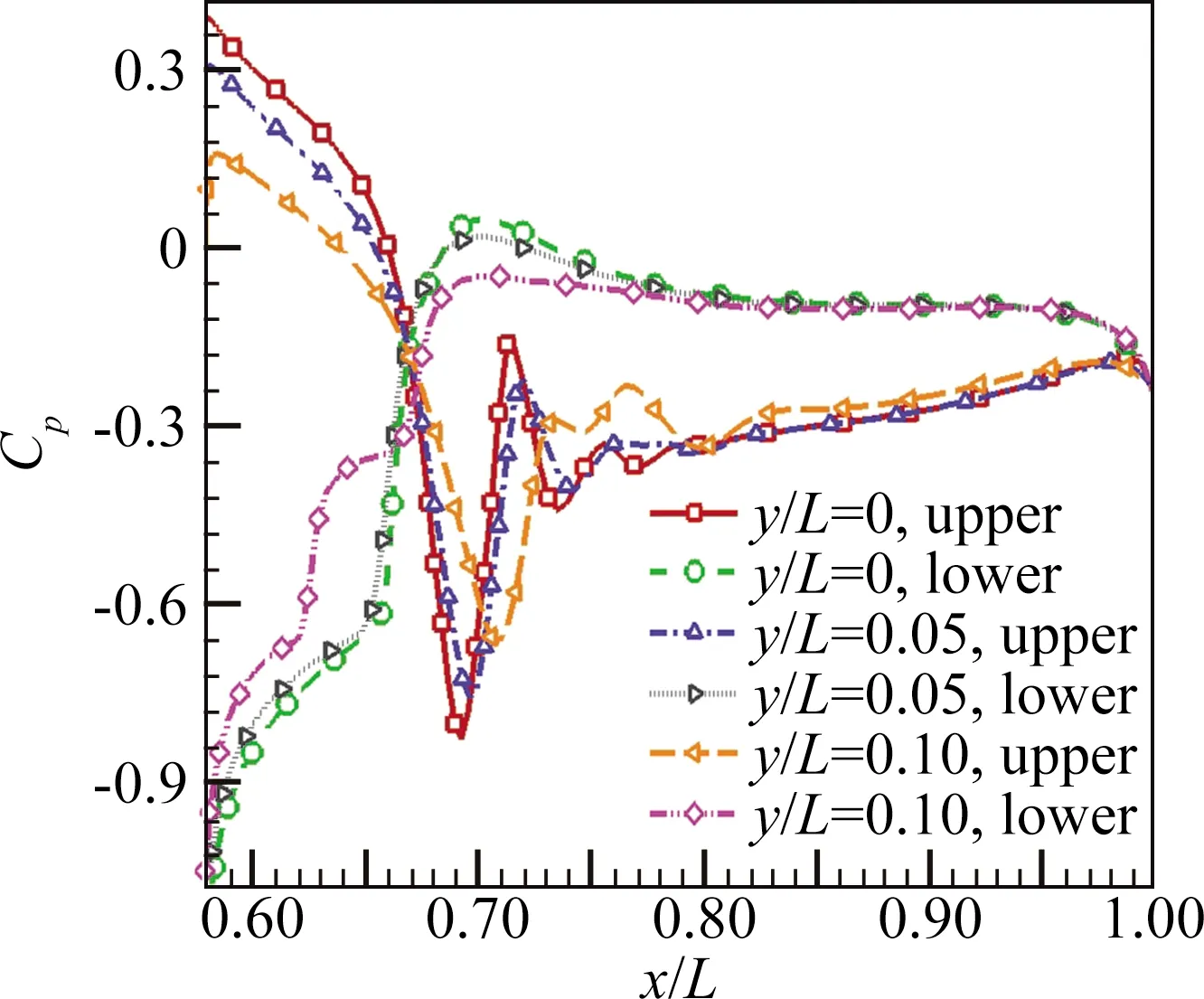
图13 高压捕获翼不同展向位置上下表面的压力分布Fig.13 Curves of pressure coefficient distribution on the wall of the HCW at different cross-sections in y direction

图14为不同展向位置截面中机体上下表面的压力分布曲线比较，图中横坐标给定的范围为高压捕获翼的前缘到后缘。依据图中曲线可知，机体物面压力沿流向先减小后增大。结合图12的马赫数分布可知，其主要原因是来流经过捕获翼与圆锥之间的收缩通道时受到压缩作用，来流速度增大，物面压力逐渐减小，在拐点附近来流加速至声速，同时由于机体的转折形成膨胀波，受其作用来流速度迅速增加，导致物面压力急剧下降，随后在圆台上表面回流区的作用下流速逐渐减小，物面压力逐渐回升。而在后部收缩段，由于分离区的存在，流动速度减小，所以壁面压力逐渐增加。此外，机体受高压捕获翼干扰区域主要为上表面的对称面附近。下表面受干扰较小，仍接近于轴对称流动，所以壁面压力分布除了y/L=0和y/L=0.05截面的上表面，其余四条曲线基本重合。在对称面上，高压捕获翼的影响最为明显，在其前缘驻点附近，马赫数减小，所以机体上表面对应的压力要高于下表面，并随展向位置增加，二者趋于一致。

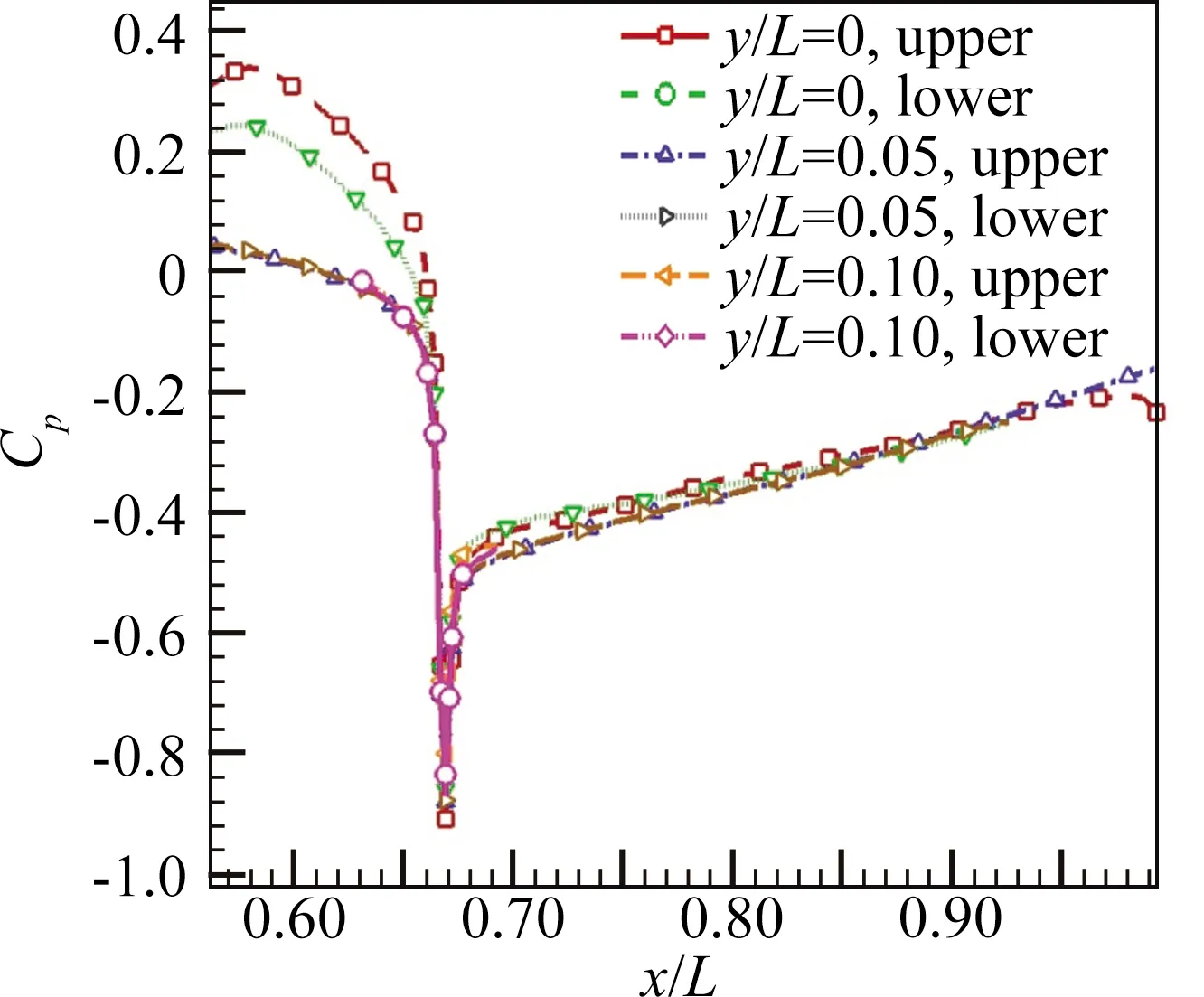
图14 机体不同展向位置上下表面的压力分布Fig.14 Curves of pressure coefficient distribution on the wall of the fuselage at different cross-sections in y direction

4 结论和讨论

本文基于一种简化的原理性构型，对高压捕获翼新型气动布局在跨声速条件下的基本流动特性进行了初步研究，获得了这类新型布局在跨声速条件下的基本特性。得到如下基本结论：

1) 在跨声速条件下，高压捕获翼与机体之间的气动耦合比较明显，这导致机体与捕获翼之间的通道内流场结构相对较为复杂，通道内产生的激波串导致捕获翼下表面的壁面压力出现明显的波动。对于实际飞行器而言，这种压力波动可能会导致在跨声速飞行条件下俯仰力矩出现较为明显的变化，进而影响其俯仰通道的稳定特性。

2) 捕获翼与机体之间的气动干扰主要集中于机体上半部分附近的区域，且越靠近对称面附近干扰越强烈，对于机体下半部分及其远离对称面的区域影响相对较弱，其原因主要是二者间距离增加所致。对于实际的飞行器而言，尽管机体下表面一般也会增加升力面并形成双翼布局，但由于双翼间距离较大，因此相互的耦合干扰应相对较弱。但对于具体实例，特别是在姿态发生变化或有诱导涡产生的条件下仍需开展更加全面和细致的分析。

为简化构型，本文中捕获翼采用平板外形，但从计算结果看，其流动结构仍与跨声速机翼基本一致。在实际中，从减弱上表面激波的角度而言，对于捕获翼截面形状可考虑超临界翼型的设计思路，在综合考虑亚/跨/超/高超飞行条件下开展多点优化，使其在宽速域条件下均具有良好的气动性能。此外，为摸清基本流动特性，本文的分析仅考虑了一种跨声速工况。下一步拟进一步拓展流动条件，包括马赫数范围、不同的姿态角以及不同雷诺数条件等，以进一步探究相关流动特性和机理。