三相-五相矩阵变换器谐波产生机理的分析研究
张 博,王汝田,文湘雲
(1.国网鞍山供电公司,辽宁 鞍山 114000;2.东北电力大学,吉林 吉林 132012)
矩阵变换器作为一大类电力电子变换器,对其研究和应用正逐渐发展起来。与传统的电力变换器相比,矩阵变换器有一系列优点:能量双向流动,四象限运行;正弦输入电流、输出电压;可控功率因数;不需要直流储能元件等[1-8]。随着研究的深入和实际应用的需要,三相输入多相输出的矩阵变换器发展起来,其中以三相-五相矩阵变换器为代表。在三相-五相矩阵变换器中,包含的开关较多,控制较为繁琐,同时谐波问题不可避免。对其输出电压的谐波分析能够为控制算法的改进和滤波电路设计提供一定的依据,并且分析方法也可推广至其他类型的矩阵变换器。
矩阵变换器的控制方法大致可分为直接控制与间接控制,文献[1-2]采用了直接控制的方法,即根据输出电压矢量和输入电流矢量直接选择合适的开关组合,文献[3-8]采用了间接控制的方法,即将矩阵变换器等效为交-直-交结构,该种结构更加便于理解,对于输出电压谐波的分析也更加方便,因此本文在将矩阵变换器转换成等效交-直-交结构的基础上在虚拟逆变级进行输出电压的谐波分析。文献[9-11]介绍了不同的五相逆变的控制算法,这些控制算法可应用到三相-五相矩阵变换器的虚拟逆变级,其中空间矢量脉宽调制(SVPWM)算法主要有最近两矢量和最近四矢量算法,并在其基础上做出相应改进。本文主要对这两种控制算法进行了分析比较并进行仿真加以验证。
1 三相-五相矩阵变换器的双空间矢量调制方法
1.1 虚拟整流级的SVPWM
一般三相-五相矩阵变换器的拓扑结构为文献[8]中的12开关输入级拓扑结构。首先假定电源电压对称,虚拟整流级的直流回路电流恒定,为后级虚拟逆变级供电。
虚拟整流级输入电流空间矢量分布与参考电流矢量的合成见图1。输入电流空间矢量由3个零矢量和6个非零矢量构成,6个非零矢量将360°电角度空间划分为6个扇区。由于输入相间不能短路,6个非零矢量中总有一相电流为0。例:图中的(1×0)表示输入a相的上桥臂导通,输入b相上下桥臂均关断,输入c相下桥臂导通。
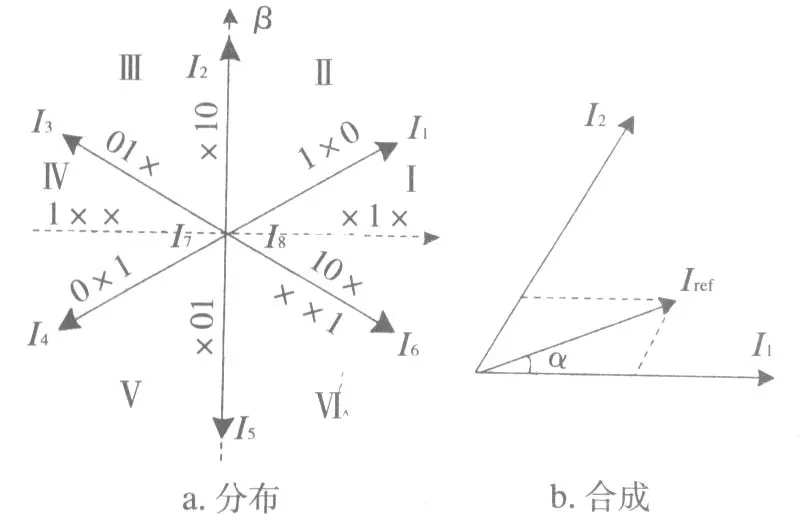
图1 输入电流空间矢量分布与参考电流矢量合成
设I1、I2及零矢量I0的作用时间分别为T1、T2和T0,则由图1根据平行四边形法则可求得:
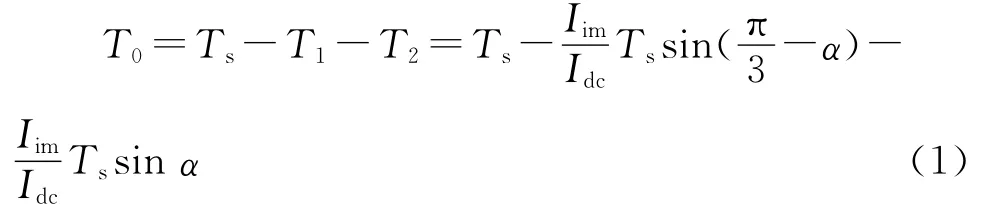
式中:Ts为开关周期;Iim为输出电流的峰值;Idc为输出的直流电流平均值。
1.2 虚拟逆变级的SVPWM
虚拟逆变级基波空间中空间电压矢量的分布见图2。其中有2个零电压矢量(对应U0和U31,下标为形成该空间电压矢量的二进制开关函数对应的十进制数),30个非零电压矢量。非零电压矢量中,将小电压矢量记为US,中电压矢量记为UM,大电压矢量记为UL,三者的模值比为1∶1.618∶1.6182。这些空间电压矢量将360°电角度空间分为10个扇区。
五相逆变SVPWM算法主要有最近两矢量算法和最近四矢量算法,两种算法的参考电压矢量合成见图3。
2 虚拟逆变级采用不同算法时输出电压的谐波分析
由SVPWM逆变的原理可知,输出各相电压由一系列方波组成,这便不可避免地产生谐波。分析谐波采用的主要方法为对输出电压进行傅里叶级数展开,由于分析方法相同而最近四矢量SVPWM算法较为复杂,因此以最近四矢量算法为例做详细分析,对最近两矢量算法的分析可按相同方法进行。
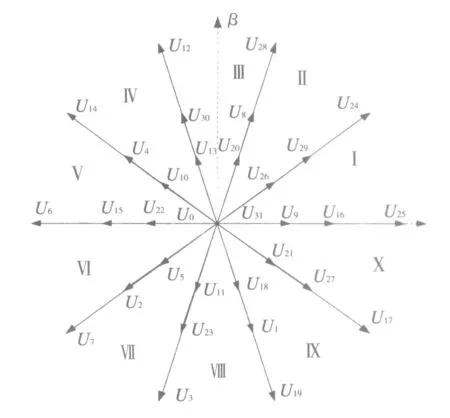
图2 基波空间中的空间电压矢量的分布
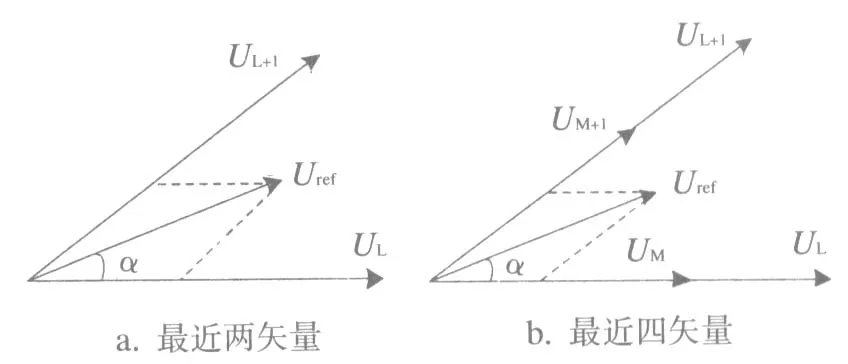
图3 两种算法参考电压的合成
2.1 采用最近四矢量SVPWM算法时输出电压的谐波分析
以A相输出电压UA(t)为例,输出电压展开为傅里叶级数可表示为:
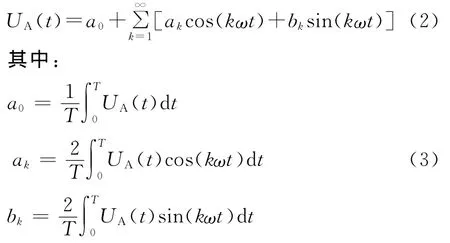
式中:k表示谐波次数;a0、ak、bk分别为0次和k次谐波电压系数;ω为角频率;T为周期。
计算时A相输出电压UA(t)可表示为:
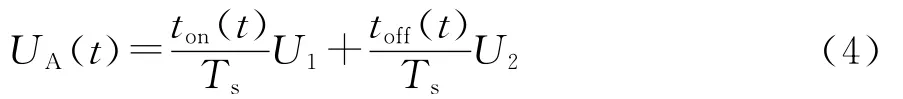
式中:ton(t)、toff(t)分别为UA(t)在一个开关周期内电压值为正和为负所对应的持续时间;U1、U2分别为UA的正电压值和负电压值。根据各矢量的特点,U1的值有Udc/5、2Udc/5、3Udc/5、4Udc/5四种,U2的值有 -Udc/5、-2Udc/5、-3Udc/5、-4Udc/5四种。根据合成参考电压Uref所在扇区的不同,U1、U2的值及其对应的作用时间也不同,以第一扇区为例,UA的值一直为正,当U16作用时其值为4Udc/5,当U29作用时其值为Udc/5,当U25作用时其值为2Udc/5,当U24作用时其值为3Udc/5,且其作用时间分 别为t′1、t′2、t′3、t′4。
由于各个扇区情况不同,积分计算也需分扇区进行,以计算ak为例,计算方法如下:
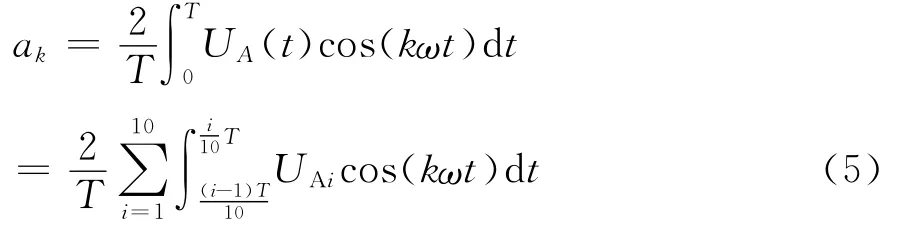
式中UAi为在各自扇区中输出电压UA的值,其由公式(4)得出,以计算ak的第一扇区为例,积分表达式可写为:
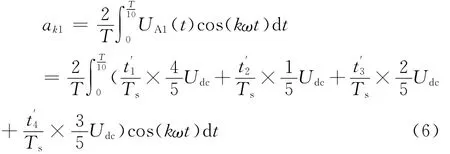
将a转换为对应的ωt,对其他扇区计算时也需做相应的变换,计算结果为:
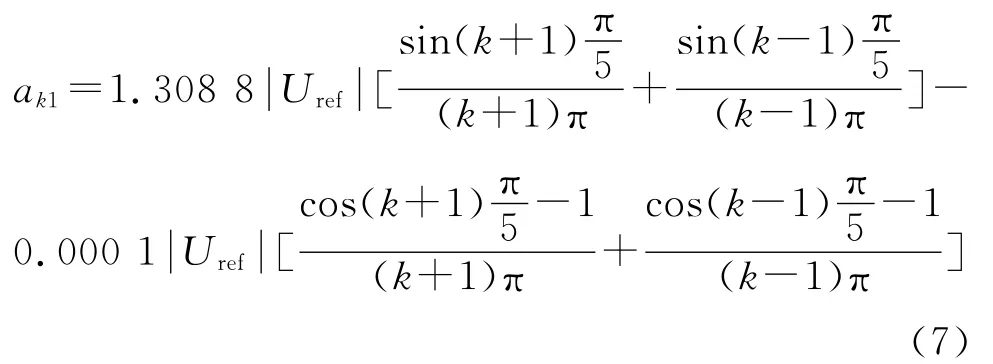
以此方法可分别求得10个扇区中谐波对应的傅里叶函数形式,将其根据公式(5)整合便可求得ak,以相同的方法可以求得bk,这样便可得到A相输出电压的傅里叶展开形式。以参考电压幅值为100V为例,将A相输出电压展开至第10次谐波的计算结果见表1。
电压谐波畸变率VTHD计算公式如下:
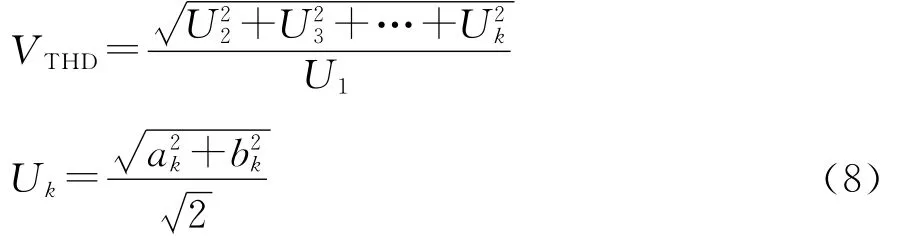
式中:Uk为第k次谐波电压有效值;U1为基波电压的有效值。将表1中的数据代入公式(5)可以得到在虚拟逆变级采用最近四矢量SVPWM算法时输出相电压谐波的畸变率为0.02%。
2.2 采用最近两矢量SVPWM算法时输出电压的谐波分析
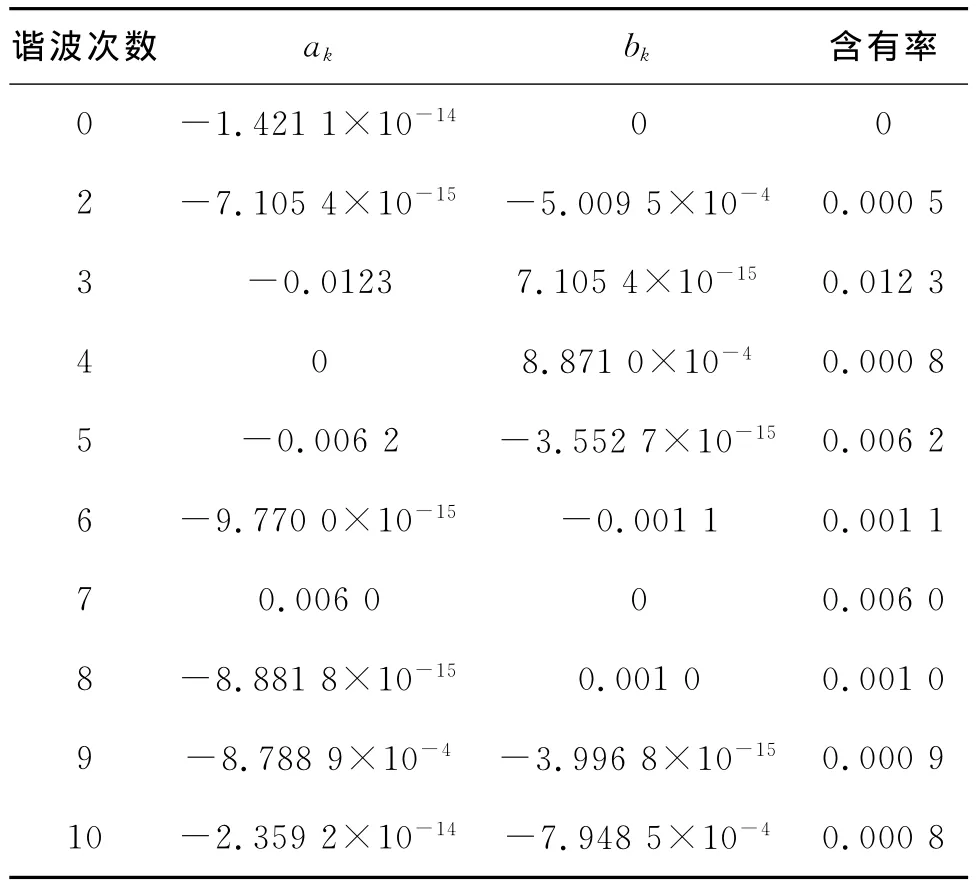
表1 最近四矢量算法A相输出电压谐波计算结果
同样采用2.1中的方法进行计算。最近两矢量算法中作用矢量较少,UA(t)对应的表达式也较为简单,限于篇幅,下面直接给出采用最近两矢量SVPWM算法时将A相输出电压展开至第10次谐波的计算结果(见表2。)
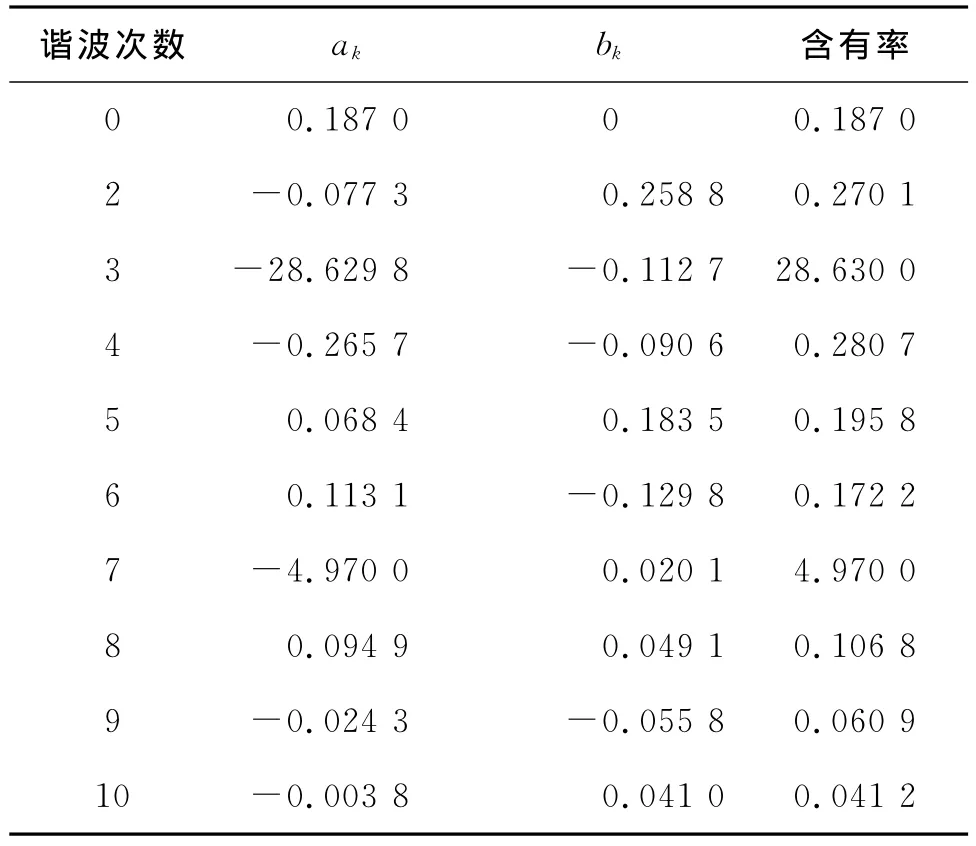
表2 最近两矢量算法A相输出电压谐波计算结果
由表2及公式(8)可以计算得出:采用最近两矢量SVPWM算法时输出相电压谐波的畸变率为29.06%。
3 仿真分析
在上述计算分析的基础上,搭建了基于Matlab/Simulink的仿真模型,通过S函数完成扇区的判断,各电压矢量及其作用时间的分配,模型参数为:三相电源相电压峰值UM=200V,输出相电压参考电压峰值Uom=100V,每相负载中R=5Ω,L=5×10-3H,开关周期Ts=1×10-4s。
采用两种不同算法所得的A相输出电压及其快速傅里叶变换(FFT)分析见图4、图5。可以看到在虚拟逆变级采用最近四矢量SVPWM算法所得的输出电压波形更加良好。对于最近四矢量SVPWM算法,仿真结果比计算的值要大,在计算时虚拟逆变级直流侧设定为恒定值,计算结果更接近理想情况。
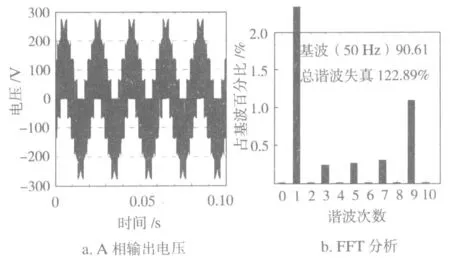
图4 最近四矢量SVPWM算法下的A相输出电压及其FFT分析

图5 最近两矢量SVPWM算法下的A相输出电压及其FFT分析
根据表1、表2和图4、图5可以发现,计算结果与仿真结果较为接近,尤其是幅值较大的各次谐波。同时可以看到,在虚拟逆变级采用最近两矢量SVPWM算法主要的谐波含量为较小的低次谐波和(5k±2)(k=1,3,5…)次谐波,且随着谐波次数的提高,谐波幅值衰减很大。
计算和仿真都表明了在虚拟逆变级采用最近两矢量SVPWM算法会产生以三次谐波为主的各次谐波,而采用最近四矢量SVPWM算法能够有效消除谐波,对三次谐波的抑制效果尤为明显。
4 结论
本文对三相-五相矩阵变换器进行了简要介绍,并主要对其输出电压进行了谐波的计算分析。虚拟逆变级输入相数较多,可以采用不同的控制算法,通过计算和仿真发现,最近四矢量SVPWM算法能够输出质量较好的电压波形,达到良好的控制效果,是一种较好的控制方法。此外,通过对控制算法的分析,也为其他类型矩阵变换器的分析、算法的改进和滤波电路的设计提供相应的依据。

