基于差分系数和参数辨识的配电网故障选线
李卫国,刘柏岑,许文文
(东北电力大学,吉林 吉林 132012)
国内配电网大多采用小电流接地(中性点不接地或经消弧线圈接地)运行方式[1]。该方式下配电网发生单相接地故障时,其故障电流微弱,故障特征不明显,所以选线问题一直以来没有得到很好的解决。由于小电流接地系统故障电流小且常发生间歇性电弧会破坏其稳态特征,因此基于故障稳态信号的选线方法如零序电流比幅法、群体比幅比相法、工频无功功率法等将会失效[2]。而对于中性点经消弧线圈接地系统发生故障,其在过补偿方式下工作,也将难以再利用工频量的故障特征来区分故障线路和非故障线路[3—4]。
随着信号处理技术的发展,故障信号中的暂态量能够被提取并进一步分析,故障信号暂态分量幅值大且故障信息丰富,在故障初始阶段不受消弧线圈的影响,因此基于暂态信号的故障选线得到了广泛的关注[5]。文献[6]对暂态零序电流进行小波变换,根据不同故障初相角时故障信号的能量谱特征不同,通过比较小波高频能量或低频能量进行选线。文献[7]利用矩阵束算法对故障后暂态零模电流进行频率分析,并提取出各线路暂态零模电流强制分量中暂态特征最明显的频率分量进行选线,但当过渡电阻较大时存在灵敏度不足的问题。文献[8]通过分析各出线是否含有衰减的直流分量来进行故障线路的判定,该方法在故障初相角为90°时,故障信号将不存在衰减直流分量,导致选线可靠性降低,该方法可作为选线的辅助判据。以上选线方法都仅利用了故障信息的一部分,很难实现可靠的故障线路识别,因此一些利用故障信息的多个故障特征选线方法如粗集理论法、模糊算法、融合算法等涌现出来,该类方法是通过借助数学工具来提高选线的可能性和可靠性,但其算法复杂且较难应用于工程实际。文献[9]从线路参数出发,提出以参数识别方式进行故障选线,利用故障线路电容极性实现基于模型电容参数的故障选线,但特征频段内包含的频率成分太少不利于选线,会产生较大的测量误差。文献[10]根据故障线路在高、低频段零序阻抗呈现不同的特性,以故障线路零序电流和母线零序电压在高、低频段的关系体现其差异并借此进行选线,但该方法不适用于中性点不接地系统。
本文将针对以上不足,对线路零序阻抗特性在整个首次串联谐振频段内差异进行分析,为充分利用不同频段的故障信息提出差分系数的概念构造选线判据,在适用性分析的基础上引入参数辨识作为补充,提出一种基于差分系数和参数辨识的选线方法。
1 线路零序阻抗特性
建立基于线路分布参数的配电网单相接地故障模型,可从传输线阻抗特性角度分析不同线路阻抗的特性。其零序等效网络见图1,图中Rs为消弧线圈电阻;Lk为消弧线圈电感;S为中性点接地方式切换开关;Rf0为接地电阻;I0n、R0n、L0n、C0n分别为线路n的零序电流、电阻、电感和分布电容。
图1中可将单相均匀的分布参数线路模型看作一个二端口网络,根据线路的传输方程可求得线路入端阻抗,(正常时)末端开路Zld=∞,则其入端Zoc为:
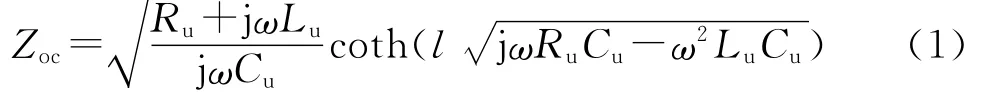
式中:Ru、Lu、Cu分别为单位线路长度电阻、电感和分布电容;ω为角频率;l为线路长度。
1.1 健全线路和故障点至负荷段线路首次串联谐振
忽略线路电阻Ru,式(1)变为:
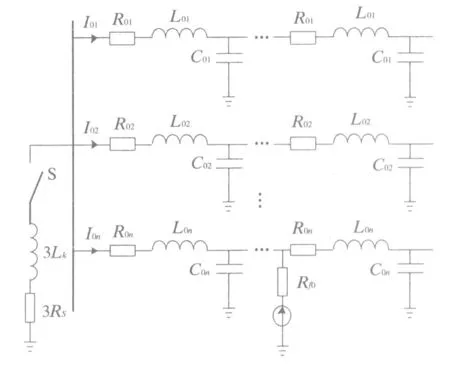
图1 配电网零序等效网络

当kπ<ωl<π/2+kπ时,Zoc为容性;当kπ+π/2<ωl<kπ+π时,Zoc为感性,k为周期数。
在ωl=π/2时,入端零序阻抗Zoc=0,线路首次发生串联谐振(阻抗由容性变为感性)。其首次串联谐振频率为:

则在0~ωos频率内,线路的零序阻抗呈电容特性;其线路阻抗可等效为Zoc=1/jωCi,Ci为健全馈线i的等值电容;而当ω>ωos时,随着频率的增加零序阻抗将交替呈现感性和容性。
1.2 故障点至母线段首次串联谐振
由文献[11]可知,对于中性点不接地系统故障线路检测到的入端阻抗是所有健全线路并联阻抗,若配电网是谐振接地系统则其入端阻抗为所有健全线路和消弧线圈的并联阻抗。而对于上述两种接地系统故障线路都存在着一个相同首次串联谐振频率。由故障线路和健全线路入端阻抗关系可知,根据所有健全线路串联谐振情况,故障线路将发生多次谐振,而故障线路首次串联谐振频率当取所有健全线路中首次发生串联谐振的最小频率(即故障线路的首容性频率)。
则故障线路最小串联谐振频率ωmin为各健全线路首次发生串联谐振频率ωos最小值,即:

由图1可知,线路n发生单相接地故障,对于健全线路和故障点下游,其测定的阻抗为线路自身入端零序阻抗,并且该部分线路在频段0<ω<ωmin内均呈容性,可等效为一集中参数电容Ci。
对于故障线路n,打开S,图1为中性点不接地系统,此种情况下其检测到的等值阻抗是所有健全线路并联阻抗Zn,可表示为:

将开关S闭合,其为谐振接地系统,故障线路检测到的等值阻抗是所有健全线路和消弧线圈的并联阻抗,而由于消弧线圈的阻抗呈感性,其产生的感性电流会对线路容性零序电流进行补偿,故障线路零序阻抗特性将发生较大的变化,其等值零序阻抗为:
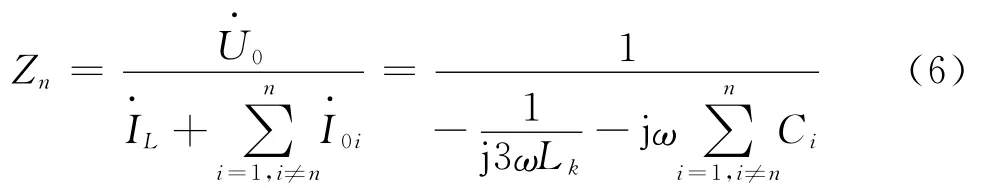
由式(6)可知,当Zn=∞时,线路发生并联谐振,其谐振频率ωn为:

谐振接地系统的消弧线圈一般采用10%左右过补偿,工频下的感性阻抗约等于所有线路的零序容抗,故ωn一般大于工频,但ωn≪ωmin;在0~ωn频段内故障线路零序阻抗呈感性;在ωn处发生并联谐振;在频段ωn~ωmin内,故障线路零序阻抗呈容性。
综上所述,各线路表现出零序阻抗特性为:对于健全线路,零序阻抗呈现容性且为正电容。对于故障线路不同的接地系统其故障线路零序阻抗特性不同,在中性点不接地系统中,其故障线路零序阻抗在整个首次串联谐振频段内都表现为容性且为负电容;而对于谐振接地系统则将整个首次串联谐振频段分成两个频率区段,在不同的频率区间其故障线路零序阻抗呈现不同的特性,在低频区段内呈感性,在高频区段呈现容性且为负电容。
2 基于馈线零序阻抗特性的选线原理
2.1 选线原理
根据具体的故障过程并结合以上分析可知,故障线路在特定频段内才能等效为电容且呈负极性,而当故障进入稳态时,故障线路在低频段将不再呈现为电容特性;对于健全线路在整个故障过程中其一直满足电容特性并呈正极性。
定义差分系数ΔX为:各线路零序电流和母线零序电压高、低频分量的差分求导。

式中:i0t、u0t、Ct分别为高频段零序电流、母线零序电压、电容;i0w、u0w、Cw分别为低频段零序电流、母线零序电压、电容;ΔC为电容差。
对于健全线路,其零序电流和零序电压在高、低频分量所求电容差值ΔC=0。对于故障线路,当该配电网为谐振接地系统,其在高频段时,零序阻抗特性呈容性,可等效为电容C′t,结合公式(6)得:
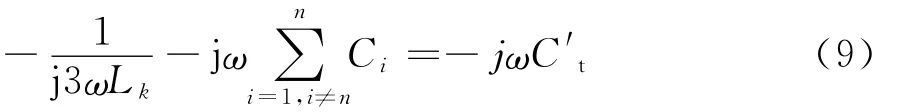
低频时,故障线路等效阻抗成感性L′w不满足式(8)关系,故障线路在低频段的零序电流为in=IDCe-t/τL+I0nsin(ωt+θ),又因为故障线路低频段阻抗呈感性,un相位滞后故障线路零序电流90°故un=-U0cos(ωt+θ)。则故障线路在故障初始阶段和稳态阶段的零序电压和电流之间的关系ΔX具体表示为:
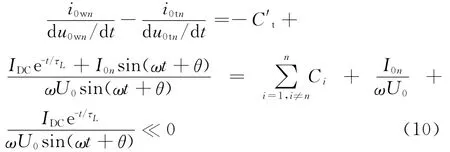
式中:i0wn、u0wn为线路n 零序电流的高频分量;i0tn、u0tn为线路n零序电流低频分量;IDC为直流衰减分量幅值;τL为电感电流时间常数。
由此可通过判据判断谐振接地系统故障线路和健全线路,若某一线路ΔX不等于0,则该线路为故障线路;若ΔX等于0,则该线路为健全线路;若所有线路均有ΔX等于0,则为母线故障。
但当系统为中性点不接地系统时,由第1节分析可知,系统所有线路求解的ΔX都将等于0,而导致上述判据无法区分线路故障和母线故障的情况。
2.2 选线判据
对于线路i,综合运用线路在高低频段阻抗特性差异和电容的极性特性,健全线路电容为正电容极性,故障线路在高频段的电容呈负电容极性。得出适用于不同接地系统的统一选线判据如下:

式中δ表示选线判据,其数值对应选线结果。
判据分析,对配电网所有线路求解δ,当δ为-1时,则该线路为故障线路,当δ为1时,该线路为健全线路;当δ小于1时,该线路为故障线路;当所有线路的δ都为1时,则为母线故障。
2.3 电容极性的识别和高、低频分量的提取
2.3.1 电容极性的识别
模型建立之后可将图1线路等效为π型,任一条健全线路其零序电压、电流满足以下关系
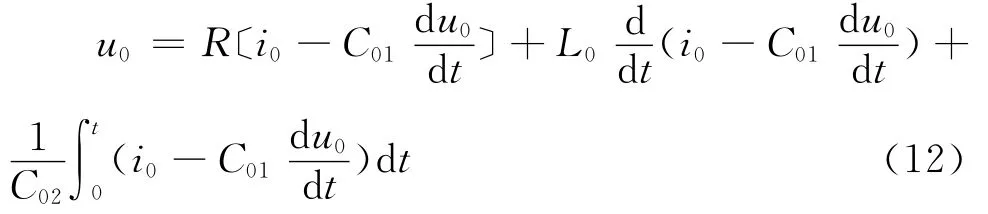
显然模型中各电压电流均已知,未知量为线路参数R0,L0,C01,C02,采取多个采样点的数据可联立得一个非线性方程组,采用最小二乘法求解出母线侧电容C01。
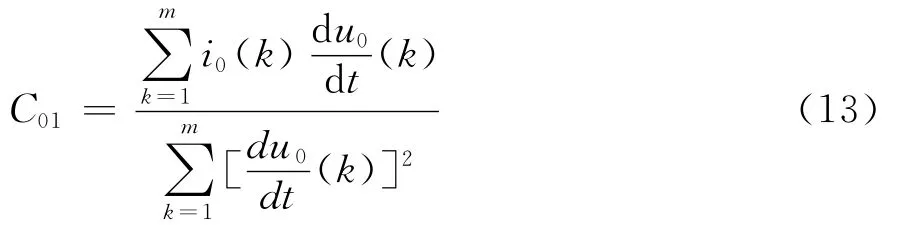
2.3.2 高、低频分量的提取
对于母线零序电压和各线路零序电流的高低频分量的提取需考虑在不同故障情况下的零序电流频率分布特点。不同的故障情况下,线路零序电流表现的故障特征存在差别。当故障初相角接近于0°时,零序暂态电流主要是衰减感性直流分量和稳态分量。当接地时刻在相电压过90°时,暂态感性电流为0,零序暂态电流主要是高频振荡的容性分量。
故障线路包含着主要的4个频率分量,衰减的直流分量、工频分量和两个高频分量。其中直流分量是消弧线圈引起的电感电流,因此健全线路中不存在这种分量,另外健全线路和故障线路能量集中频段不同。根据上述健全线路和故障线路频谱以及分量的差异可实现高低频的分界频率的预估,从而有效的提取零序电压和电流信号的低频分量和高频分量,此过程需借助滤波器实现,上述分析中采用的是线路某一位置故障,而实际上由并联谐振频率其与故障位置有关,因此无法确定并联谐振的具体值,因此通过提取能量集中频率点设定ωmin。另本文选取3倍的工频作为其区分高低频分量的一个界限频率点。这里需采用频率范围为150Hz~ωmin/2π的带通滤波器和频率范围为0~150Hz低通滤波器进行高、低频分量的获取。
2.4 选线流程
a.当母线零序电压瞬时值u0大于设定阈值kUN(其中k一般取0.15,UN为母线额定电压),启动故障选线。
b.采集故障后2个工频周期的母线零序电压u0和各馈线的零序电流i0k,根据π型线路模型线路参数约束关系,采集6组数据形成非线性方程组并采用最小二乘法识别电容及其极性,C>0正极性,C<0负极性。
c.通过滤波器提取高、低频段的母线零序电压u0和各馈线的零序电流i0;对于母线电压的高、低频分进行差分求导得du0t/dt、du0w/dt,将高、低频下零序电流分量i0t、i0w和差分求导后母线零序电压分量du0t/dt、du0w/dt代入公式(8)得到各馈线的差分系数ΔX。
d.将各馈线的电容极性C和高、低频下差分系数ΔX代入(11)求得δ,将各线路的δ与设定的阈值进行比较。故障选线流程见图2。
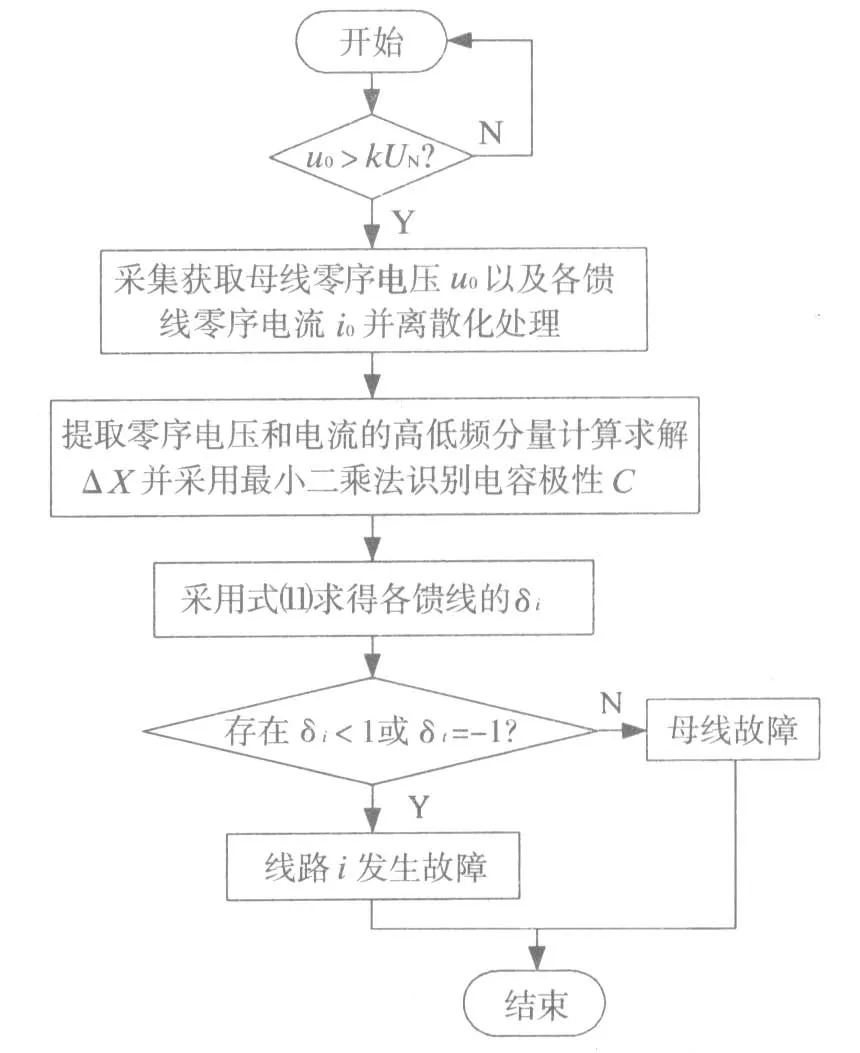
图2 故障选线流程图
3 仿真及其适应性分析
3.1 仿真模型
利用Matlab/Simulink仿真平台搭建10kV小电流接地配电网仿真模型,其仿真示意图见图3,其中的主变压器变比为110∶10,线路L1~L5长度分别为16、8、20、18、10km。线路正、负序电阻R1=R2=0.27Ω/km,零序电阻 R0=2.7Ω/km;正、负序电容C1=C2=3.39×10-7F/km,零序电容C0=280×10-3F/km;正、负序电感L1=L2=2.55×10-10H/km,零序电感L0=1.02×10-3H/km;各条线路等效负荷统一采用Z1=400+j200。
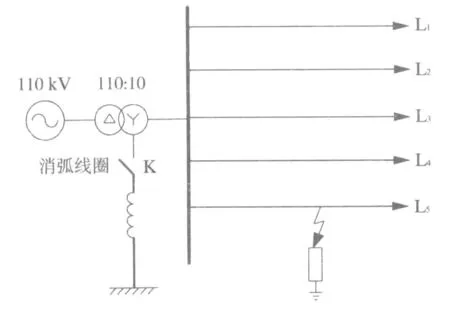
图3 仿真示意图
3.2 仿真验证
3.2.1 中性点不接地时的选线情况
打开上述图3中的开关K即系统为中性点不接地系统,通过设置不同的过渡电阻Rf、不同故障时刻θ、不同故障距离d的单相接地故障验证该方法选线效果。
设定线路L5发生单相接地故障,其过渡电阻为50Ω,故障初始角90°时的选线情况,现以线路L1和L5的差分系数ΔX和选线判据δ对本文所提方法选线情况作简要分析(见图4)。中性点不接地系统时线路L1和L5的差分系数都为0,而通过线路L1和L5电容极性差别可判断出故障线路L5。

图4 健全线路L1和故障线路L5的ΔX和δ
在线路L5上6km处发生单相接地故障,当故障初相角90时°,改变过渡电阻其选线结果见表1;当过渡电阻为50Ω时改变故障初相角其选线结果见表2。

表1 不同过渡电阻下的各馈线ΔX/δ及选线结果

表2 不同故障初相角下各馈线ΔX/δ及选线结果
由表1和表2仿真结果可以看出,本文方法能够在不同的故障环境即不同过渡电阻、故障初相角情形下准确定位故障线路,且在不接地系统中故障线路L5和其他健全下路极性差别较为明显,故障结果清晰。
在线路L5设置单相接地故障,在故障初相角90°,过渡电阻50Ω,不同故障距离时其选线结果见表3。由仿真结果可知,当故障距离为0时,时其在高频和低频两种状态下求解的ΔXi=0,根据电容极性进行线路判定,所有线路电容为正极性,δ都为1,由判据判定为母线故障;不同故障距离下均可准确判定故障线路为L5。
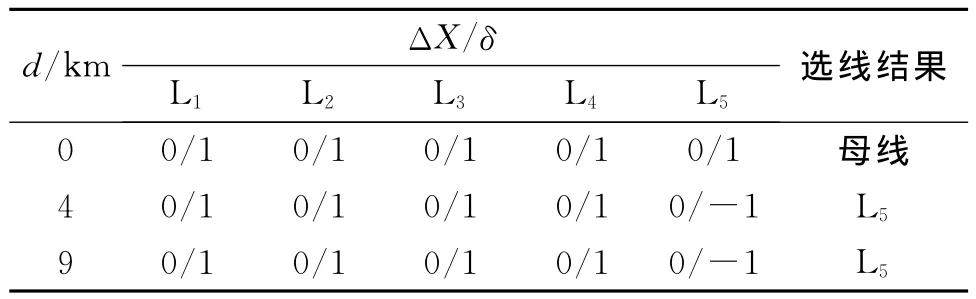
表3 不同故障距离下各馈线ΔX/δ及选线结果
3.2.2 谐振系统选线情况
仿真验证本文方法对中性点经消弧线圈接地系统单相接地故障选线效果,闭合图3中的开关K,仿照不接地系统设置仿真参数。为保证选线不受波动的影响设定选线阈值当0.9<δ<1.1,取δ=1。具体的在不同过渡电阻、故障初始角下和故障距离的仿真结果见表4、表5、表6。

表4 不同过渡电阻下的各馈线ΔX/δ及选线结果
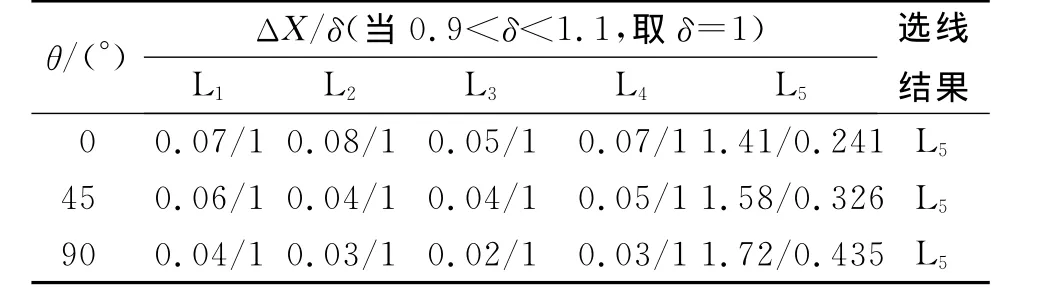
表5 不同故障初相角下各馈线ΔX/δ及选线结果

表6 不同故障距离下各馈线ΔX/δ及选线结果
由表4、表5、表6可知,该方法的适用性较强,可应用于中性点经消弧线圈接地系统,此种情况下虽故障线路差分系数不再为零,但故障线路的判据结果δ明显小于1,在过渡电阻较大时或是故障初始角较小时,仍能准确的选出故障线路,对于不同故障距离、母线故障,也能满足选线准确适应性强的需要。
4 结论
a.本文基于线路零序阻抗特性分析,得出由于各健全线路以及消弧线圈的并联谐振,故障线路的零序阻抗特性在首容性频段内以并联谐振为界分成两个频段,在低频段内线路零序阻抗成感性,高频段内零序阻抗成容性。
b.分析了在高频段和低频段下健全线路和故障线路零序电流与其母线零序电压导数的比值的差值关系,不相同且差异明显,但其不适用于不接地系统,针对该不足引入了参数辨识(电容),利用中性点不接地时故障线路和健全线路电容极性差异特点加以补充。
c.提出了应用整个首次串联谐振频段故障信息且适用于不同中性点接地系统的选线判据。该方法可充分利用故障后母线和馈线在不同频段的暂态信息,而仿真结果表明,该方法能够适用于不同过渡电阻、不同故障初始角、不同故障距离及母线故障的故障选线,具有自举性。

