基于双曲面球型减隔震支座的铁路简支梁桥桥墩地震损伤分析

许敏，魏标，刘义伟，张伦，李姗姗，颜璐

基于双曲面球型减隔震支座的铁路简支梁桥桥墩地震损伤分析

许敏1，魏标2, 4，刘义伟3，张伦5，李姗姗6，颜璐2, 4

(1. 中铁二院工程集团有限责任公司，四川 成都 610031；2. 中南大学 土木工程学院，湖南 长沙 410075；3. 江西省交通设计研究院有限责任公司，江西 南昌 330052；4. 高速铁路建造技术国家工程实验室，湖南 长沙 410075；5. 成兰铁路有限责任公司，四川 成都 610032；6. 江苏建筑职业技术学院 智能制造学院，江苏 徐州 221116)

由于双曲面球型减隔震支座作为一种新型支座在铁路桥梁中应用较少，采用ABAQUS软件建立8 m及25 m墩高的铁路简支梁桥有限元模型，研究双曲面球型减隔震支座减少桥墩地震损伤的效果，并对数值仿真结果进行振动台试验验证。研究结果表明：双曲面球型减隔震支座减少铁路简支梁桥桥墩地震损伤的能力远大于普通球型支座，且在大多数情况下能有效防止桥墩进入屈服状态；采用双曲面球型减隔震支座时，8 m墩的地震损伤减少的效果明显好于25 m墩，且25 m墩在高烈度地震作用下屈服的可能性较高。

双曲面球型支座；铁路简支梁桥；减隔震；非线性时程；地震损伤

在中国已经完成的旅客专用线和高铁中，一部分路线至少70%使用的是桥梁形式[1]。地震灾害是铁路建设中不可避免要考虑的问题，进行铁路桥梁在高地震烈度地区的减隔震设计研究非常有必要。双曲面球型减隔震支座使用大半径球面摩擦副替代了普通球型钢支座中的平面摩擦副[2]，同时加入抗剪结构，其工作原理与传统的摩擦摆支座基本相同，但是位移能力更大。通过研究某3跨门式桥墩轨道交通曲线连续梁桥罕遇地震下的地震响应，顾正伟等[3]应用SAP2000有限元软件，分析了双曲面球型减隔震支座在轨道连续梁桥中的减隔震效果。刘俊等[4]结合工程实例研究了此种新型支座的摩擦因数和球心距对桥梁抗震设计控制截面内力的影响；聂晋涛[5]通过研究穿越地震断裂带的某旅客专用铁路桥，分析了此种新型支座的减隔震效果。现有研究大多基于公路桥，且内容重点通常在桥梁结构的受力大小，而不是桥梁的结构动力行为，故此种双曲面球型隔震支座在铁路简支梁桥中的应用仍亟待研究。本文基于墩高8 m以及25 m的单线铁路简支梁桥，建立单墩有限元模型，利用ABAQUS中的“混凝土损伤塑性模型”对铁路简支梁桥的桥墩地震损伤进行模拟；并且通过振动台缩尺实验分别对设置普通支座和双曲面球型减隔震支座的模型桥墩底部损伤程度进行验证。通过与普通球型支座对比，评价双曲面球型减隔震支座减少桥墩地震损伤的效果。

1 桥梁与地震

1.1 铁路简支梁桥原型

铁路简支梁桥原型为适用于新建客运专线铁路工程的单线有砟轨道预制后张法两片式预应力混凝土T型简支梁桥。

如图1所示，该简支梁桥的梁高为2.7 m，计算跨度为32 m，全长为32.6 m，从轨底到梁底之间的建筑高度是3.4 m，直线二期恒载是101.26 kN/m，单线主梁的自重是297.6 t。

图1 梁体横断面

如图2所示，选取圆端型实体8 m矮墩和25 m中高墩进行研究。其中8 m墩墩身为等截面，而25 m墩墩身则按35:1的比例变化，材料皆为C35混凝土，并采用HRB400钢筋。

图2 桥墩

1.2 铁路简支梁桥有限元模型

本文采用ABAQUS软件进行有限元分析。双曲面球型减隔震支座的有限元模型如图3所示，采用C3D8R实体单元模拟底座板、中座板(含聚四氟乙烯板)、上座板3个部分。通过在顶座板与梁底之间定义不同的绑定或摩擦属性，分别模拟滑动支座与固定支座。支座的基本设计参数如下：活动支座纵向正常位移为±30 mm，竖向承载能力为3 000 kN，地震位移为±100 mm，滑动面摩擦因数为0.023 5，滑动面球心距为1 500 mm。

图3 新型支座有限元模型

本文采用Connector单元模拟普通球型支座，单元平动及转动使用“Cartesian+Cardan”约束。固定支座3个方向的平动自由度全部被约束，同时释放支座3个方向的转动自由度；滑动支座则约束竖直向和横桥向的平动自由度，释放了桥向平动以及3个转动自由度，同时定义顺桥向摩擦属性，摩擦因数为0.03。

铁路简支梁桥有限元模型见图4，为单墩模型。简支梁、桥墩和承台混凝土均采用C3D8R实体单元模拟。桥墩钢筋采用truss单元建立，采用T3D2属性划分网格，使用“embedded”约束模拟钢筋和混凝土之间的共同承载，同时不考虑钢筋与混凝土之间的黏结滑移效应。桥墩两侧各为半跨简支梁，分别由滑动支座和固定支座支承，约束梁体绕轴与轴的转动自由度。对桥墩墩底区域进行网格加密并定义“混凝土损伤塑性”属性。模型忽略轨道结构[6−7]，忽略桩土效应影响，将地震荷载视为直接作用于承台底部[8]。

1.3 地震工况

选取2条自然地震波和1条人工波作为地震荷载[9]。自然地震波为常用的Kobe波和Northridge波，人工地震波通过计算机程序拟合生成，每条地震波分别按加速度峰值0.2，0.3和0.4共3个水准进行调幅。将地震荷载输入铁路简支梁桥有限元模型。

(a) 8 m墩；(b) 25 m墩

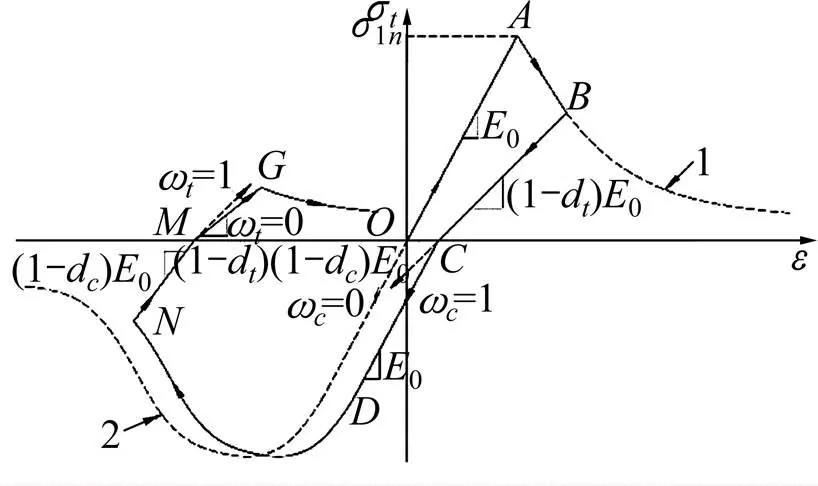
1—单轴拉伸；2—单轴压缩。

2 桥墩混凝土损伤属性

桥墩混凝土的地震损伤采用ABAQUS中的“混凝土损伤塑性模型”进行模拟。“混凝土损伤塑性模型”基于塑性混凝土连续损伤行为，通过各向同性的拉伸、压缩塑性理论和弹性损伤理论来表征混凝土的非弹性行为。该模型可以模拟混凝土机械行为作用下的循环、动态和单调载荷，而断裂过程中出现的不可逆损伤行为可以使用将各向同性弹性损伤理论以及非关联多重硬化塑性理论结合起来的方法模拟。

(a) 8 m墩−滞回曲线；(b) 8 m墩−骨架曲线；(c) 25 m墩−滞回曲线；(d) 25 m墩−骨架曲线

CDP模型在单轴循环荷载作用下的混凝土应力应变关系如图5所示。图5中0为材料初始无损伤弹性刚度；d和d为混凝土拉伸损伤变量、压缩损伤变量，用来描述受拉、受压破坏程度；和作为拉伸刚度恢复因子和压缩刚度恢复因子，被用来控制反向荷载下拉伸和压缩刚度的恢复程度。如果默认=0和=1，受拉刚度不恢复，受压刚度完全恢复。

3 桥墩低周反复荷载作用分析

对8 m和25 m墩铁路简支梁桥有限元模型进行低周反复荷载分析，以墩顶水平位移为横坐标绘制墩顶水平反力的滞回曲线以及骨架曲线，如图6所示。由图6可知，桥墩在初始阶段保持弹性状态，在墩顶水平位移达到一定程度后会出现较为明显的屈服现象。

设置普通支座和双曲面球型减隔震支座的桥墩墩底弯矩计算公式1和2分别如式(1)和式(2)所示。其中：F是桥墩的等效惯性力；c是惯性力等效作用点高度；是桥墩高度；F是普通支座下梁的惯性力；F是双曲面球型减隔震支座的摩擦力。由于2种支座下桥墩的惯性力分布区别不大，所以此处2种情形下的F和取相同的值。

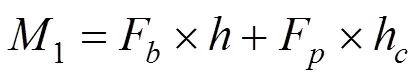
根据桥墩低周反复荷载作用的计算结果，将8 m墩和25 m墩的受力性能按墩顶水平位移分为弹性阶段、带裂缝工作阶段和屈服阶段，如表1所示。

表1 桥墩受力性能阶段

4 桥墩地震损伤分析

4.1 8 m墩地震损伤

以Kobe波顺桥向作用的地震工况为例，采用双曲面球型支座和普通支座时，8 m墩铁路简支梁桥的墩底区域的混凝土损伤对比如图7所示。由图7可以看出，采用双曲面球型减隔震支座时，8 m墩在0.2，0.3和0.4地震作用下都没有出现损伤；采用普通支座时，8 m墩在0.2地震作用下即出现了较大范围的损伤，损伤范围随地震烈度的增加而增加。

定义损伤区域在桥墩顺桥向中心线中的总长度为损伤深度，统计8 m墩在所有工况下的最大损伤深度、墩顶位移、墩底混凝土应变、墩底钢筋应变4个数据，结果如表2所示。以墩底钢筋屈服或墩顶位移达到7.9 mm作为桥墩屈服的判断条件，由表2可得：

1) 应用普通支座时，8 m墩在0.2地震作用下已达到屈服状态，损伤程度随地震烈度增加而 增加。

2) 应用双曲面球型减隔震支座时，8 m墩在0.2地震作用下没有损伤；在0.3地震作用下可能出现小范围的受拉损伤；在0.4地震作用下出现损伤的概率和程度增大，但桥墩不会达到屈服状态。

(a) 0.2g-双曲面球型支座；(b) 0.2g-普通球型支座；(c) 0.3g-双曲面球型支座；(d) 0.3g-普通球型支座；(e) 0.4g-双曲面球型支座；(f) 0.4g-普通球型支座

4.2 25 m墩地震损伤

以Kobe波顺桥向作用的地震工况为例，采用双曲面球型支座和普通支座时，25 m墩铁路简支梁桥的墩底区域的混凝土损伤对比如图8所示，即混凝土单元的拉伸损伤变量d的值。由图8可以看出，采用双曲面球型减隔震支座时，25 m墩在0.2地震作用下没有出现损伤，在0.3和0.4地震作用下都出现了一定程度的受拉损伤；采用普通支座时，25 m墩在0.2地震作用下已出现了较大范围损伤，损伤范围随地震烈度增加而增加。

表2 8 m墩地震损伤

注：8 m墩顺桥向宽度2 100 mm；混凝土应变达到107×10−6时开始出现受拉损伤；钢筋应变达到2 000×10−6时屈服。

(a) 0.2g-双曲面球型支座；(b) 0.2g-普通球型支座；(c) 0.3g-双曲面球型支座；(d) 0.3g-普通球型支座(e) 0.4g-双曲面球型支座；(f) 0.4g-普通球型支座

定义损伤区域在桥墩顺桥向中心线中的总长度为损伤深度，统计25 m墩在所有工况下的最大损伤深度、墩顶位移、墩底混凝土应变、墩底钢筋应变4个数据，结果如表3所示。以墩底钢筋屈服或墩顶位移达到32.2 mm作为桥墩屈服的判断条件，由表3可得：

1) 应用普通支座时，25 m墩在0.2地震作用下已达到屈服状态，损伤程度随地震烈度的增加而增加。

2) 应用双曲面球型减隔震支座时，25 m墩在0.2地震作用下没有损伤；在0.3地震作用下会出现一定程度的损伤，但不会达到屈服状态；在0.4地震作用下桥墩会达到屈服状态。

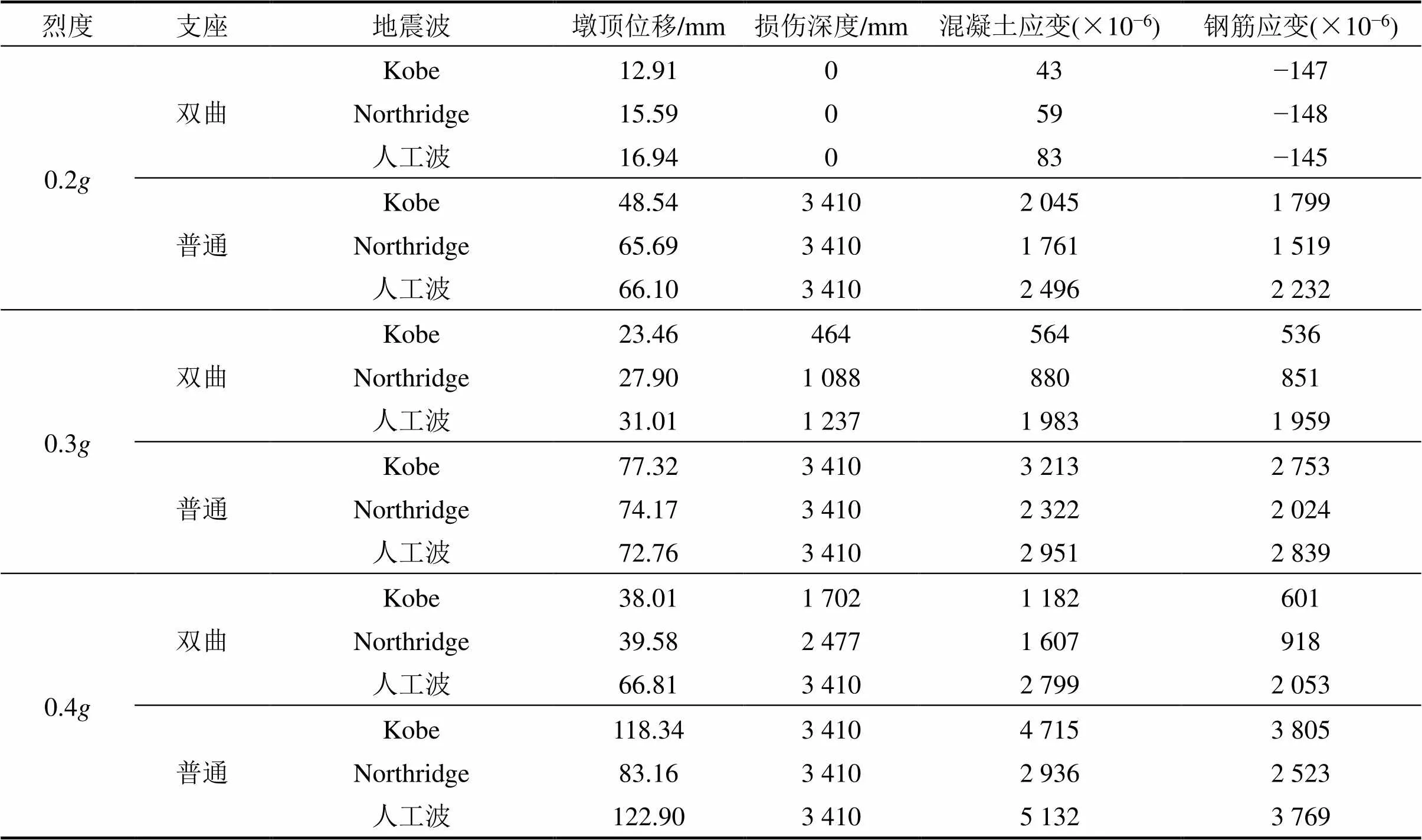
表3 25 m墩地震损伤

注：25 m墩顺桥向宽度3 410 mm；混凝土应变达到107×10−6时开始出现受拉损伤；钢筋应变达到2 000×10−6时屈服。

5 振动台试验验证

5.1 试验工况

本文以“设置了普通支座和双曲面球型减隔震支座的铁路桥梁模型抗震实验”为依据，对有限元模型的桥墩底部损伤程度进行验证。该试验(见图9)是长度、位移相似比为1/7的缩尺模型振动台试验，其凹形摩擦面的曲率采用周期等效原则进行缩尺，设置的2种支座均采用和原型相同的材料[10]。理论上，相同地震作用下的试验缩尺模型变形应该为数值仿真桥梁原型的1/7。试验模型材料弹性模量和强度采用相似比1/1，即采用与桥梁原型相同的材料。理论上，相同地震作用下的试验缩尺模型应力应变关系应该与数值仿真桥梁原型基本一致。

为了保持相同的地震动输入，在数值仿真桥梁原型地震动输入的基础上，根据缩尺理论对地震波进行缩尺后，沿试验缩尺模型顺桥向输入地震动。

(a) 8 m墩缩尺模型；(b) 25 m墩缩尺模型

5.2 试验结果对比

沿纵桥向依次输入0.2，0.3和0.4的地震波后，安装双曲面球型支座和普通球型支座的桥墩墩底损伤情况见图10。总体规律如下：

1) 图10(a)显示安装双曲面球型支座的8 m桥墩墩底完好，与图7(e)的数值仿真结果基本一致。

2) 图10(b)显示安装普通球型支座的8 m桥墩墩底出现明显裂缝，与图7(f)数值仿真结果基本一致，但图10(b)相较图7(f)裂缝分布更加集中。

3) 图10(c)显示安装双曲面球型支座的25 m桥墩墩底出现轻微裂缝，与图8(e)的数值仿真结果基本一致。在安装相同双曲面球型支座的情况下，图10(c)中的25 m桥墩墩底损伤程度大于图10(a)中的8 m桥墩墩底损伤程度。

4) 图10(d)显示安装普通球型支座的25 m桥墩墩底出现明显的裂缝，与图8(f)的数值仿真结果基本一致，但图10(d)相对于图7(f)的裂缝分布更加集中。在安装相同普通球型支座的情况下，图10(d)中的25 m桥墩墩底损伤程度小于图10(b)中的8 m桥墩墩底损伤程度。

(a) 8 m墩底−双曲面支座；(b) 8 m墩底−普通支座；(c) 25 m墩底−双曲面支座；(d) 25 m墩底−普通支座

振动台模型试验主要记录了桥墩墩顶位移、桥墩墩底保护层混凝土应变和纵筋应变。将振动台试验记录结果与表2和表3的计算结果进行比较，其比值分别如表4和表5所示，主要规律如下：

1) 振动台试验结果总体上大于数值仿真结果。在桥墩损伤程度较小的情况下，振动台试验结果与数值仿真结果较为接近，误差可以控制在35%以下；在桥墩损伤程度较大的情况下，振动台试验结果与数值仿真结果相差较大，最大误差达到51%；当桥墩损伤情况很大时，部分应变片损坏，无法记录试验数据。

2) 相对于表5的25 m墩比值，表4的8 m墩比值存在更大误差，主要是因为：8 m墩损伤程度总体上较大；8 m墩弯剪耦合严重、应力分布复杂，即使采用实体单元模拟，仍然存在较大模拟误差。

振动台试验结果与数值模拟结果存在一定误差，但两者的总体趋势相同，数值模拟结果在总体上可信。

表4 8 m墩试验结果与数值仿真结果对比

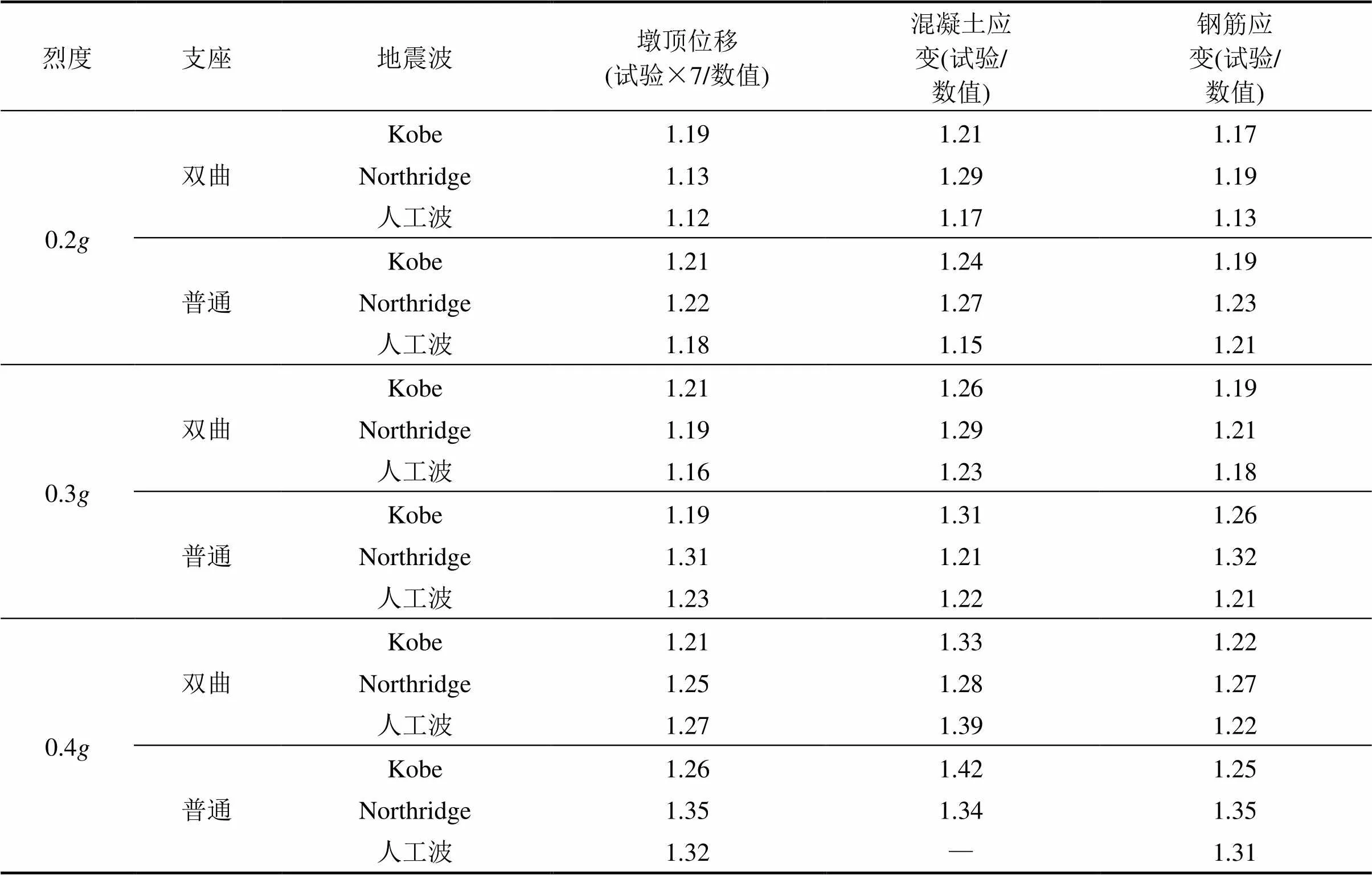
表5 25 m墩试验结果与数值仿真结果对比

6 结论

1) 双曲面球型减隔震支座能大幅减少铁路简支梁桥的桥墩地震损伤的范围和损伤，有效防止桥墩进入屈服状态，对桥墩具有良好的保护效果。

2) 采用双曲面球型减隔震支座，对减少8 m墩的地震损伤的效果明显好于25 m墩，且25 m墩在高烈度地震作用下屈服的可能性较高。

3) 与公路桥墩不同，铁路桥墩质量不可忽略。尤其在铁路桥墩略高时，桥墩质量甚至远远超过主梁质量。虽然在墩梁连接处设置双曲面球型减隔震支座有一定效果，但无法避免铁路桥墩在强震下的损伤。

[1] 余志武, 何华武, 蒋丽忠, 等. 多动力作用下高速铁路轨道−桥梁结构体系动力学及关键技术研究[J]. 土木工程学报, 2017, 50(11): 1−9. YU Zhiwu, HE Huawu, JIANG Lizhong, et al. Dynamics and key technology research on high-speed railway track-bridge system under multiple dynamic sources[J]. China Civil Engineering Journal, 2017, 50(11): 1−9.

[2] WEI Biao, YANG Tianhan, JIANG Lizhong, et al. Effects of friction-based fixed bearings on the seismic vulnerability of a high-speed railway continuous bridge [J]. Advances in Structural Engineering, 2018, 21(5): 643−657.

[3] 顾正伟, 钟铁毅, 张贞阁. 双曲面球型减隔震支座曲线连续梁桥的减隔震[J]. 中国铁道科学, 2011, 32(3): 47− 51. GU Zhengwei, ZHONG Tieyi, ZHANG Zhenge. Seismic isolation of curved continuous bridge with double spherical aseismic bearing[J]. China Railway Science, 2011, 32(3): 47−51.

[4] 刘俊, 王合希. 双曲面球型减隔震支座在刚构连续梁桥中的应用[J]. 铁道科学与工程学报, 2012, 9(3): 117− 123. LIU Jun, WANG Hexi. Application of double spherical seismic isolation bearing in a rigid frame-continuous girder bridge[J]. Journal of Railway Science and Engineering, 2012, 9(3): 117−123.

[5] 聂晋涛. 客运专线桥梁中减隔震技术应用研究[J]. 铁道工程学报, 2012, 29(3): 53−57. NIE Jintao. Research on application of seismic reduction and isolation technology in bridge of passenger dedicated line[J]. Journal of Railway Engineering Society, 2012, 29(3): 53−57.

[6] 张永亮, 于伟栋, 马华军, 等. 板式无砟轨道系统对不同抗震体系铁路桥梁纵向地震响应的影响[J]. 中南大学学报(自然科学版), 2017, 48(10): 2738−2744. ZHANG Yongliang, YU Weidong, MA Huajun, et al. Influence of slab ballastless track on longitudinal seismic response of railway bridge with different seismic systems [J]. Journal of Central South University (Science and Technology), 2017, 48(10): 2738−2744.

[7] 魏标, 杨添涵, 蒋丽忠. 轨道结构建模精细化程度对高速铁路连续梁桥地震易损性的影响[J]. 工程力学, 2018, 35(4): 16−23. WEI Biao, YANG Tianhan, JIANG Lizhong. The effects of model refinement of ballastless tracks on the seismic vulnerability of a continuous bridge on a high-speed railway[J]. Engineering Mechanics, 2018, 35(4): 16−23.

[8] 魏标, 李建中. 基于位移的非规则梁桥抗震设计[J]. 土木工程学报, 2011, 44(8): 95−101. WEI Biao, LI Jianzhong. Displacement-based seismic design of irregular continuous bridges[J]. China Civil Engineering Journal, 2011, 44(8): 95−101.

[9] WEI Biao, YANG Tianhan, JIANG Lizhong, et al. Effects of uncertain characteristic periods of ground motions on seismic vulnerabilities of a continuous track-bridge system of high-speed railway[J]. Bulletin of Earthquake Engineering, 2018, 16(9): 3739−3769.

[10] WEI Biao, ZUO Chengjun, HE Xuhui, et al. Numerical investigation on scaling a pure friction isolation system for civil structures in shaking table model tests[J]. International Journal of Non-Linear Mechanics, 2018, 98(1): 1−12.

Seismic damage analysis of simply-supported railway bridge piers based on double spherical seismic isolation bearings

XU Min1, WEI Biao2, 4, LIU Yiwei3, ZHANG Lun5, LI Shanshan6, YAN Lu2, 4

(1. China Railway Eryuan Engineering Group Co. Ltd, Chengdu 610031, China;2. School of Civil Engineering, Central South University, Changsha 410075, China; 3. Communications Design & Research Institute Co. Ltd. of Jiangxi Province, Nanchang 330052, China;4. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China;5. Chengdu-Lanzhou Railway Co. Ltd, Chengdu 610032, China; 6. School of Intelligent Manufacturing, Jiangsu Vocational Institute of Architectural Technology, Xuzhou 221116, China)

As a new type of bearing, the application of double spherical seismic isolation (DSSI) bearing in railway bridges is relatively few. The finite element models of simply-supported railway bridge with 8 m and 25 m piers were established by using ABAQUS software, and the effects of DSSI bearings on reducing the pier seismic damage were studied. Finally, the numerical analysis results were validated by the shaking table tests. The results show that when compared with ordinary spherical bearing, DSSI bearing can significantly reduce the seismic damage range and degree of simply-supported railway bridge piers, and effectively prevent the piers fromreaching a yield stage in most cases. The effects of DSSI bearings on reducing the seismic damage of 8 m pier are better than that of 25 m pier, and the 25 m pier has a high possibility of reaching a yield stage under high intensity earthquakes.

double spherical bearing; simply-supported railway bridge; seismic isolation; nonlinear time history; seismic damage

10.19713/j.cnki.43−1423/u.T20190942

U24

A

1672 − 7029(2020)07 − 1769 − 09

2019−10−24

四川省科技计划资助项目(2019YFG0048)；国家自然科学基金资助项目(51778635，51778630)；湖南省自然科学基金资助项目(2019JJ40386)；江苏省住房和城乡建设厅资助项目(2017ZD012)；高烈度地震区(成兰)铁路桥墩抗震综合试验专题(CLRQT-2015-010)

魏标(1982−)，男，江苏铜山人，教授，博士，从事桥梁抗震研究；E−mail：weibiao@csu.edu.cn

(编辑 涂鹏)