一类具有潜伏感染细胞的时滞病毒感染模型*

杨俊仙，于淑妹

（安徽农业大学理学院，安徽合肥230036）

传染病是由各种病原体引起的能在人与人、动物与动物或者人与动物之间相互传播的一类疾病［1］。大多数传染病是通过病毒感染来实现的，因此运用数学建模的方法对传染病病毒感染的动力学行为进行研究，对传染病的预防和控制均具有重要意义［2-5］。最初的病毒感染模型是由Nowak 和Perelson 等提出［6-8］，形式如下：

其中x(t)，y(t)，v(t)分别表示t时刻未感染细胞数、被感染细胞数和病毒数。参数λ 表示未感染细胞的固有生成率，β 表示病毒感染率，d，a，u 分别表示未感染细胞、被感染细胞和病毒的死亡率，k示病毒复制率，λ，β，d，a，u，k均为正数。

在模型（1）中，假定t 时刻未感染细胞数和病毒数之间的发生率是双线性的，然而实际发生率可能并不是完全线性的［9-11］。另外以上提到的模型忽略了一个事实，即在细胞中并不是所有的病毒都能启动活性病毒的产生。也就是说，一部分细胞在被病毒激活感染后，进入染病阶段，但还有一部分细胞在被激活之后长时间保持静止，仍然保留在潜伏期［12-13］，这种保留在潜伏期的细胞被定义为潜伏感染细胞。这种持续潜伏在细胞内的特性目前被认为是细胞从感染中恢复的障碍，但目前，在病毒感染模型中考虑潜伏感染细胞影响的模型并不多见［14-17］，其中Wang［17］讨论了一类具有潜伏感染细胞和饱和发生率的HIV-1传染病模型：

其中时滞τ1表示CD4+T 细胞与病毒接触并成为潜伏感染细胞所需要的时间，τ2表示CD4+T 细胞与病毒接触并被感染所需要的时间，τ3表示病毒产生时滞，α1> 0，α2> 0，其它参数的生物学意义同上。

系统（3）满足初始条件

1 解的有界性和平衡点的存在性

1.1 解的有界性

定理1 设(x(t)，ω(t)，y(t)，v(t))是模型（3）满足初始条件（4）的解，则解x(t)，ω(t)，y(t)和v(t)是最终有界的。

证明 定义函数

1.2 平衡点的存在性

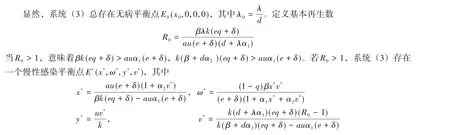
2 平衡点的全局稳定性

2.1 无病平衡点E0(x0，0，0，0)的全局渐近稳定性

2.2 慢性感染平衡点E*(x*，ω*，y*，v*)的全局渐近稳定性

3 数值模拟

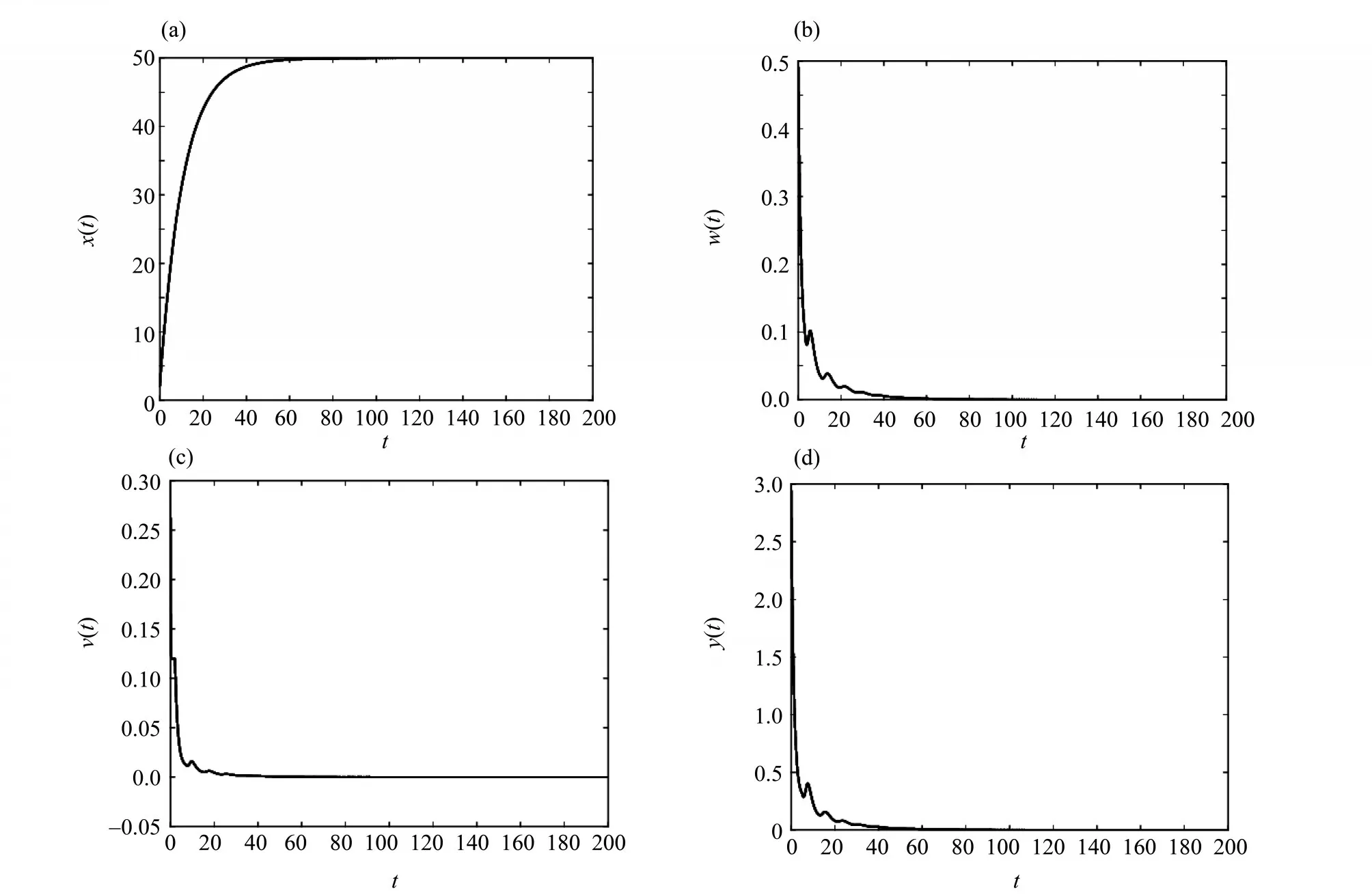
图1 当R0 ≤1时，无病平衡点E0的时间序列图Fig. 1 When R0 ≤1，time series diagram of infection-free equilibrium E0

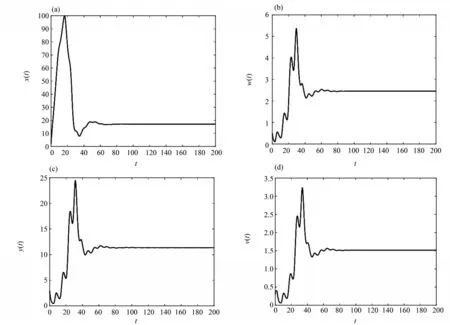
图2 当R0 > 1时，τ1 = 3，τ2 = 5，τ3 = 2时，平衡点E*的时间序列图Fig. 2 When R0 > 1，τ1 = 3，τ2 = 5，τ3 = 2，time series diagram of equilibrium E*

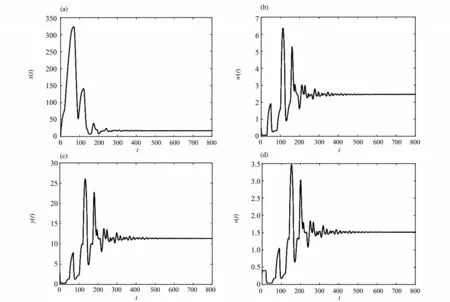
图3 当R0 > 1时，τ1 = 30，τ2 = 50，τ3 = 20时，平衡点E*的时间序列图Fig. 3 When R0 > 1，τ1 = 30，τ2 = 50，τ3 = 20，time series diagram of equilibrium E*

4 结 论

本文研究了一类具有潜伏感染细胞和Beddington-DeAngelis 发生率的时滞病毒感染模型，讨论了系统（3）的无病平衡点E0和正平衡点E*的全局渐近稳定性。结论表明：当R0≤1 时，对任意τ1≥0，τ2≥0，τ3≥0，系统（3）的无病平衡点E0是全局渐近稳定的，即在这种情况下，细胞没有被传染；当R0> 1时，对任意τ1≥0，τ2≥0，τ3≥0，系统（3）的慢性感染平衡点E*是全局渐近稳定的，即CD4+T 细胞被病毒感染后，一部分被激活进入染病阶段，但另一部分在被激活之后长时间保持静止，这种持续潜伏的状态成为细胞从感染中恢复的障碍，应引起大家的重视。在后期的研究中，我们会进一步考虑加入免疫应答细胞以及免疫时滞的情形。