内部比对试验结果的统计评价方法

(成都飞机工业(集团)有限责任公司检验检测部,成都 610092)

在实验室常使用标准物质或质量控制物质、测量设备的期间核查、实验室内比对等方式对试验过程进行监控。同时,在 AC7101/1G:2019《NADCAP对所有材料实验室的总体要求》的附录中要求各申请专业每年度需按照一定频次完成能力验证和内部比对试验,对于一些专业还专门提出了对人员的内部比对和对设备的内部比对的频次要求。为适应中国合格评定国家认可委员会(CNAS)的“确保结果有效性”的要求、国家航空航天和国防合同方授信项目(NADCAP)的实验室内部比对要求,我实验室将不同设备之间的比对、不同人员之间的比对、与外部实验室的比对均纳入计划作为实验室进行质量控制的强有力的手段,以评价人员和(或)设备产生试验结果的重复性,从而确定实验室人员、设备能力,识别实验室存在的问题,明确不同试验者和(或)设备产生的试验结果的离散程度。

对于上述比对试验的结果,一直以来各个实验室都有多种评价方法,导致评价结果五花八门。如何针对不同的试验类型,制定切实可行的比对计划,选取易于获得的样品,采取简单、高效、科学的评价方法,是各实验室都很关心的焦点。本文针对不同内部比对试验类型,比较了几种不同的统计评价方法,得出了一些可供借鉴的结论。

1 使用已知参考值样品的比对试验

如果使用已知认定值的样品或已知平均值及其标准偏差的样品或已知样品参考值上下限范围的样品来进行比对试验,那么一般实验室会制定一个可接受范围来评价比对试验结果。

例如,AC 7101/1G:2019中规定在内部比对试验中,如果使用已知样品参考值上下限范围,那么所有测定值应落在上下限范围内;如果使用已知平均值及其标准偏差的样品,那么该项目的所有测定值落在平均值±1倍的样品标准偏差范围内,就认为设备或者人员是合格的。如果测定值落在平均值±2倍标准偏差和±1倍标准偏差之间,就需要进行额外的测定和评价(见 AC 7101/1G:2019《NADCAP对所有材料实验室的总体要求》附录D.3.2.C.c.ii.)。

如果使用认定值(或其他准确参考值)的样品,还可以使用F检验和t检验来检验有限数量样品测定的平均值与标准样品认定值(或其他准确参考值)有无显著性差异[1],即判断某种测定方法的分析结果是否可靠,见公式(1):

式中:t为统计量;μ为认定值;n为测定次数;s为标准偏差;为测定值的平均值。

判断标准:t≥t表,有显著性差异,结果不可靠;t＜t表,无显著性差异,结果可靠。t表是根据之前设定的显著性水平α,查自由度n-1的“t检验临界值表”得到。

2 使用未知参考值样品的比对试验

2.1 确定样品的参考值

在实验室进行内部比对试验时,大部分情况所使用的是未知参考值的样品,特别是对于力学性能试验,很难得到认定值已知的样品。对于这种情况下的比对试验,AC 7101/1G:2019中提到可以由实验室来确定样品的平均值和标准偏差,但至少要进行12次测定,然后再分别进行人员比对或设备比对。另外,实验室也可以参照给标准物质定值的方法,进行样品的均匀性检验、稳定性检验,剔除异常值后得出样品的参考值分布。若能得到样品的参考值及其分布,那比对试验的结果就很容易进行判断。

2.2 F 检验和t检验

对于参考值未知的样品,还可以使用F检验和t检验来比较不同分析人员的分析结果相符合的程度,即两平均值之间是否有显著性差异。但是对于使用F检验和t检验,推荐只针对二组值之间的比较,若用于多组数据的比较,计算量大,过程繁琐。比如,在实验室内部有n名人员的情况下,要完成一次内部的人员比对,若仍然采用该检验方法二二比较,就需要至少次的计算。以3个总体均值相等的检验为例,分别对两总体均值相等性进行检验,需要进行3次检验,若每次检验的置信水平为95%,那么3次检验后,置信水平将降低为0.953＝0.857,即只有85.7%,总体数目越多,置信水平越低,错误风险将变得太大[2],这将使得这种比较方法不再具有实际价值。

t值计算公式[1]为:

式中:x1为第1 组样品测定值的平均值;x2为第2组样品测定值的平均值;n1为第1组样品的测定次数;n2为第2 组样品的测定次数;S合为合并标准差。

S合计算见公式(3):

式中:S1为第1 组样品测定值的标准差;S2为第2组样品测定值的标准差。

判断标准:t≥t表,表示二组平均值之间有显著性差异;t＜t表,表示二组平均值之间无显著性差异。其中t表是根据之前设定的显著性水平α,查自由度n1＋n2-2的“t检验临界值表”得到。在用t检验前,必须进行F检验,除非已知其方差一致。

2.3 稳健统计的Z 比分数(中位值和标准化四分位距法)

有些实验室将能力验证的评价方法,运用到实验室内部比对中。CNAS-GL002:2018《能力验证结果的统计处理和能力评价指南》以及GB/T 28043-2011《利用实验室间比对进行能力验证的统计方法》等指导性文件中提到有些统计量:中位值、标准化四分位距、稳健变异系数、稳健Z比分数等。这些统计量受极端值的影响较小,这种特性叫稳健性。在对能力验证的统计计算中,经常使用Z比分数,它是基于检测结果符合正态分布的统计学原理,使用中位值和标准化四分位距的一种简单的稳健统计方法。应用此法计算得到数据总体均值和总体标准差的估计值——中位值(med)和标准化四分位距(NIQR)。中位值和标准化四分位距是数据集中和分散的度量,与平均值和标准差相似。

对于单一样品(第i个样品)的测定结果xi而言,简单的稳健Z比分数(用Z表示)为:

式中:med(x)表示一组从小到大排列的x1,x2,…,xi,…,xn的中位值;NIQR(x)表示一组从小到大排列的x1,x2,…,xi,…,xn的标准化四分位距。

四分位距(IQR)、NIQR 的计算见公式(5)和公式(6):

式中:Q1为下四分位数;Q3为上四分位数。

对一组由小到大排列的数据:居于下四分之一位置的数据为下四分位数或低四分位数(Q1),该组数据的四分之一低于Q1,四分之三高于Q1;居于上四分之一位置的数据为上四分位数或高四分位数(Q3),该组数据的四分之一高于Q3,四分之三低于Q3。简单来说,对于N个从小到大排列的数据,中位值的位置位于(N＋1)/2处,下四分位数Q1位于[(N＋1)/2＋1]/2 处,上四分位值Q3位于(N＋1)/2＋[(N＋1)/2＋1]/2-1处。

用Z比分数评定准则为:|Z|≤2,表明结果“满意”,无需采取进一步措施;2＜|Z|＜3,表明结果“有问题”,产生警戒信号;|Z|≥3,表明结果“不满意”,产生措施信号。

实验室内部的人员比对若使用稳健统计的Z比分数,参与评价的是每个个体多次测定得到的平均值,对参与统计分析的人员数量有一定要求,不能太少,并且每个参与者所用的试样都应均匀一致,稳定可靠。

例如,26个操作者进行2024金属材料拉伸比对试验,每人重复3次,将每个操作者得到的抗拉强度平均值进行顺序排列和计算,得到2024金属材料抗拉强度的Z比分数,见表1。表1中:IQR＝Q3-Q1＝472.92-470.08＝2.84;NIQR＝0.741 3×IQR＝2.10。

从每个操作者的Z比分数可以看出:操作者24的Z比分数为2.22,位于2＜|Z|＜3,表明结果“有问题”,产生警戒信号,需对操作者24 的数据进行研究。

表1 2024金属材料抗拉强度的Z 比分数Tab.1 Z-scores for tensile strength of 2024 metal material

采用稳健统计的Z比分数,对于多人的比对试验结果计算,计算量不大,结果判断科学、合理、直观。使用Z比分数对实验室能力进行评价,使用的超差判据|Z|≥3 的置信概率对应于正态分布的99.73%,即测1 000次才出现2～3次超差,属小概率。一般在一次试验中是不可能出现的,一旦出现则属于离群值。类似的,当2＜|Z|＜3时,表示概率约在95%～99%之间,出现的几率也较小。一旦出现应该周密地分析一下,是什么问题导致分散性加大。

2.4 检验一致性的方法(h 统计量和k 统计量)

参照标准GB/T 6379.2-2004《测量方法与结果的准确度(正确度与精密度)第2部分:确定标准测量方法重复性与再现性的基本方法》、ISO 5725-2:1994《测量方法与结果的准确度(正确度与精密度)第2部分:确定标准测量方法重复性与再现性的基本方法》、ASTM E 691-2018《开展实验室间研究以确定试验方法精度的规程》,为了研究一种测定方法的精密度,需要在多个协同实验室间开展研究,即在多个实验室之间采用同样的方法对同一测定样本进行相同水平的重复测定,对所有协同实验室的数据进行重复性标准差和再现性标准差估计。这种检验结果一致性的方法,虽然是用在对测定方法精密度的研究中,本文也尝试将这种方法用在实验室内部的比对试验中。

在检验一致性的方法中,需用到曼德尔的h统计量和k统计量。h表示的是实验室间一致性的统计量,k表示的是实验室内一致性的统计量。

对于每个个体采用公式(7)计算h值:

式中:d为单个个体偏差;为单个个体平均值的标准偏差。

d的计算见公式(8):

式中:p为参与比对的个体数目。

对每个个体采用公式(10)计算k值:

式中:s为单个个体的标准偏差;sr为材料的重复性标准偏差。

s的计算见公式(11):

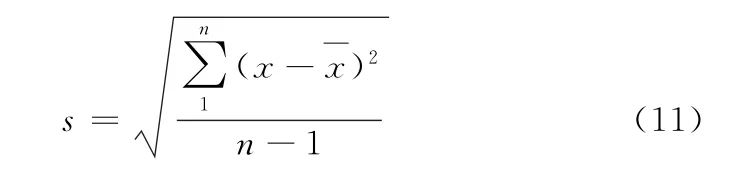
式中:n为单个个体重复测定次数;x为测定值。sr的计算见公式(12):

根据以上计算,可以计算得到每个个体的h和k值。取显著性水平为0.5%,查0.5%显著水平下h和k的极限值表,如果每个个体计算得到的h值和k值超过极限值或接近极限值,那么可以分析判断该个体的比对试验结果是否可以接受。

例如,对于上文提到的26个操作者,每人重复3次的2024金属材料拉伸比对试验,采用h和k统计量,重新进行了分析,2024金属材料抗拉强度的h和k统计量见表2,表2中,操作者p＝26,重复次数n＝3,＝2.19,sr＝2.24。

表2 2024金属材料抗拉强度的h 和k 统计量Tab.2 Statistic h and statistic k for tensile strength of 2024 metal material

对于同样26 个操作者,重复3 次的情况,查0.5%显著水平下h和k的极限值分别为2.62,2.23;查1%显著水平下h和k的极限值分别为2.43,2.09;查5%显著水平下h和k的极限值分别为1.90,1.71。可见提高显著性水平,试验数据中超过极限值的异常数据会增多,这会增加实验室不必要的成本。在实验室可接受风险范围内,一般对比查找0.5%显著水平下h和k的极限值。对照表2可以发现,操作者4的k统计量已经超过极限值,其3次试验数据重复性较差,并且操作者24的h统计量已经接近极限值,其试验数据虽然重复性较好,但与其他人的数据有差异,应引起重视。对比上文用Z比分数得到的分析结果,可以发现操作者24的Z比分数为2.22,位于2＜|Z|＜3,表明结果“有问题”,产生警戒信号。这两种分析结果都得出了同样的结论,而且使用h和k统计量比用Z比分数更能发现试验结果的重复性是否有问题。选取的置信水平稍有不同,导致使用Z比分数和使用h统计量进行判断的结论稍有不同,但趋势是一致的。

3 结语

总的来说,对于实验室内部的比对试验,本文尝试摸索了针对不同的试验类型,选取不同的适用统计评价方法。一般来说,若对比的样本只有2个,比如是2台设备之间的比对或2个人员的比对,那么就推荐使用“F检验和t检验”。若对比的样本量较大,比如超过9个人员之间的比对,使用“稳健统计的Z比分数”、“h统计量和k统计量”都是可行的,但需注意的是:①若使用Z比分数,最好提前规划好比对的个体样本数目,否则计算复杂,易出错。②在使用Z比分数时,参与计算的是单个个体重复测定后的平均值。③如果比对的样本量超过6个,或条件允许,推荐使用“h统计量和k统计量”。h可以表示个体之间的一致性,k可以表示个体内部的一致性。使用该统计方法,参与分析的不光有单次测定的数据,还有个体的平均值。可以非常直观地发现问题。