自动驾驶车辆偏航控制方法

李学鋆，陈小兵

(1.湖北汽车工业学院 汽车工程学院，湖北 十堰 442002；2.湖北汽车工业学院 汽车动力传动与电子控制湖北省重点实验室，湖北 十堰 442002)

0 引言

路径跟踪控制是自动驾驶车辆控制与决策的最终执行行为，其目的是为了保证车辆沿着预定轨迹行驶。偏航控制是路径跟踪过程中出现的复杂非线性控制问题。倪兰青等[1]以横摆角速度和横向误差距离为输入，控制车辆转向角，保证车辆对路径的实时跟踪。刘凯等[2]通过研究地形因素对车辆转向特性和稳定性的影响，建立了高速车辆的等效动力学模型，并提出一种变步长的模型离散化方法，以在车辆避障与操控稳定性发生冲突时优先保证车辆的无碰撞轨迹。王家恩等[3]利用期望横摆角速度与速度的关系，控制车辆换道跟踪控制。汪伟等[4]以侧向偏差和侧向偏差率为模糊控制器的输入，对车辆路径跟踪进行控制。汪选要等[5]基于模糊控制理论设计了车道偏离防避系统(Lane Departure Avoidance Systems, LDAS)人机共驾模糊控测器，纠正车辆偏航。除此之外，对于车辆偏航控制，还有PID(proportion integral differential)控制[6]、模糊控制(fuzzy logic controller)[7]、神经网络控制[8]等控制方法，这些控制方法是以单点预瞄理论[9]为基础，预瞄侧偏距离和车辆位姿角，最终调节车辆侧向位移，但未考虑车辆在回归点位姿角和预定轨迹回归点角度的重合，即车辆回归点的姿态角与规划轨迹的方向角度不重合，使得车辆需要二次甚至多次纠正才能回到预定轨迹。

本文通过对路径规划得到的曲线进行解耦处理，获取转向曲线，计算得到车辆在各点的预定转向角。根据路轨迹曲线的凹凸特性，提出一种圆弧回归方法，提高车辆轨迹跟踪的准确性和实时性。

1 车辆偏航模型的设计

1.1 轨迹曲线的处理

为了找出路径规划曲线与车辆转角的关系，计算出曲线各点的曲率：

(1)

车辆一旦沿着规划路径行驶，速度和时间便确定一个唯一的坐标点，即坐标x和y都可以看成是车辆行驶速度和时间的函数，即

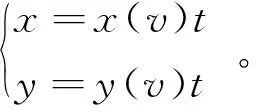
(2)

由于轨迹曲线连续光滑，即处处可导，则可对速度求偏导，得到：

(3)

对式(3)求关于速度的二次偏导，得

(4)

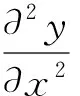
(5)

根据式(5)可以得到：

(6)

式中：速度v是车辆实时车速；δ为车辆转向角。

式(6)表明，对于已经规划好的路径曲线，可以得到车辆转向角以及车速与路径各点的关系，只要车辆沿着规划的路径行驶，其在轨迹任意点上的转向角只与路径曲线有关。

1.2 车辆偏航模型的设计

车辆在轨迹跟踪过程中可能因为环境干扰等因素出现偏航，与预定轨迹出现偏差，为了保证车辆可以及时回到预定轨迹，必须对车辆偏航进行控制。以轨迹曲线的凹凸性来界定偏航，针对偏航作如下定义：

(1)车辆回归前的Δt时间段内的车辆实际轨迹曲线与理想轨迹曲线的凹凸性一致，实际轨迹Δt时间段包围对应的理想轨迹曲线且车辆实际轨迹曲线大于理想轨迹曲线的凹凸性时，或者理想轨迹包围实际运行轨迹Δt时间段且车辆实际轨迹曲线小于理想轨迹曲线的凹凸性时，为正向偏航；反之则为负向偏航。

(2)实际轨迹Δt时间段包围对应的理想轨迹曲线且车辆回归前的Δt时间段内的车辆实际轨迹曲线与理想轨迹曲线的凹凸性不一致，为正向偏航；反之则为负向偏航。

(3)车辆回归前的Δt时间段内的车辆实际轨迹曲线与理想轨迹曲线的凹凸性有一方为零，则为负向偏航。函数凹凸性通常采用二次导数进行判断：

(7)

式中y″>0时，为凸函数，反之为凹函数。

首先针对正向偏航进行讨论，车辆正向偏航的简化图如图1所示。

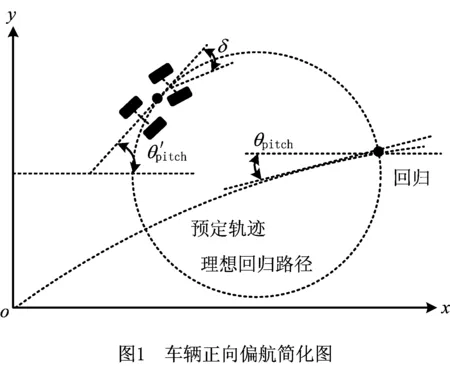
由图1可知，车辆当前位置与速度和转向有关。为了计算出偏航车辆行驶汇入预定路径的交点，本文假定车辆当前速度为纠偏行驶速度，结合路面附着力，以保证车辆不出现侧滑和侧翻为前提条件，计算出当前车速下车辆能够达到的最大转弯半径Rrectify。

保证车辆不出现侧滑的条件是：

F+Fg≤Froll。

(8)

式中：

(9)

Fg=127m(i+μLateral)。

(10)

式中：Froll为路面附着力(单位：N)，Froll=mgμLateral；i为道路超高横坡度。

可以得到：

Rrectify(max 1)

(11)

转弯过程中还可能存在车辆侧翻的安全问题，避免侧翻的条件是回正力矩大于侧倾力矩。在此过程中，路面超高也会产生部分侧倾力矩，即

∑MLateral+∑M≤∑T，

(12)

即

(13)

由此可得：

(14)

(15)

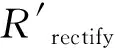
(16)

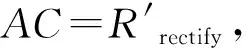
(17)

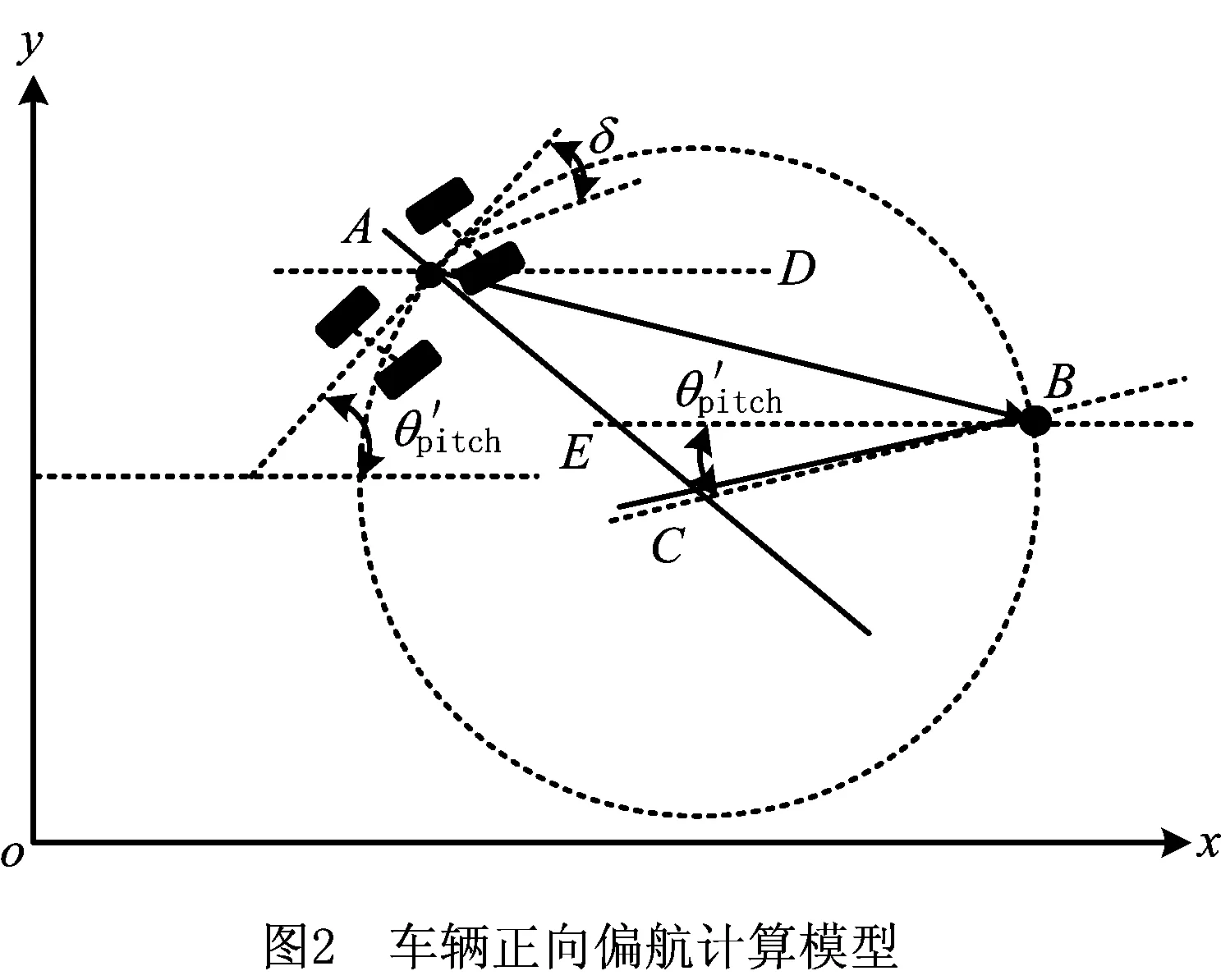
此时，车辆沿着理想回归路径可以保证车辆行驶速度最快、回归时间最短，但车辆到达回归点并不满足回归点姿态，即车辆主轴线与回归点切线不重合。为了跟踪路径，车辆主轴线与回归点切线必须重合才能保证车辆回归预定轨迹，因此必须对理想回归路径进行修正。

为了保证车辆更快抵达回归点，且保证车辆回归姿态，分别以当前位置车辆主轴线为切线和中心点为切点，以回归点为切点和回归点切线为切线作圆，两圆半径相等且外切，外切点为交点。如图3所示，联结起点、交点、回归点3点的圆弧路径即为车辆的回归路径，此时不仅可以保证车辆的回归速度，还可以保证车辆在回归点的姿态与预定轨迹重合，简化图如图3所示。

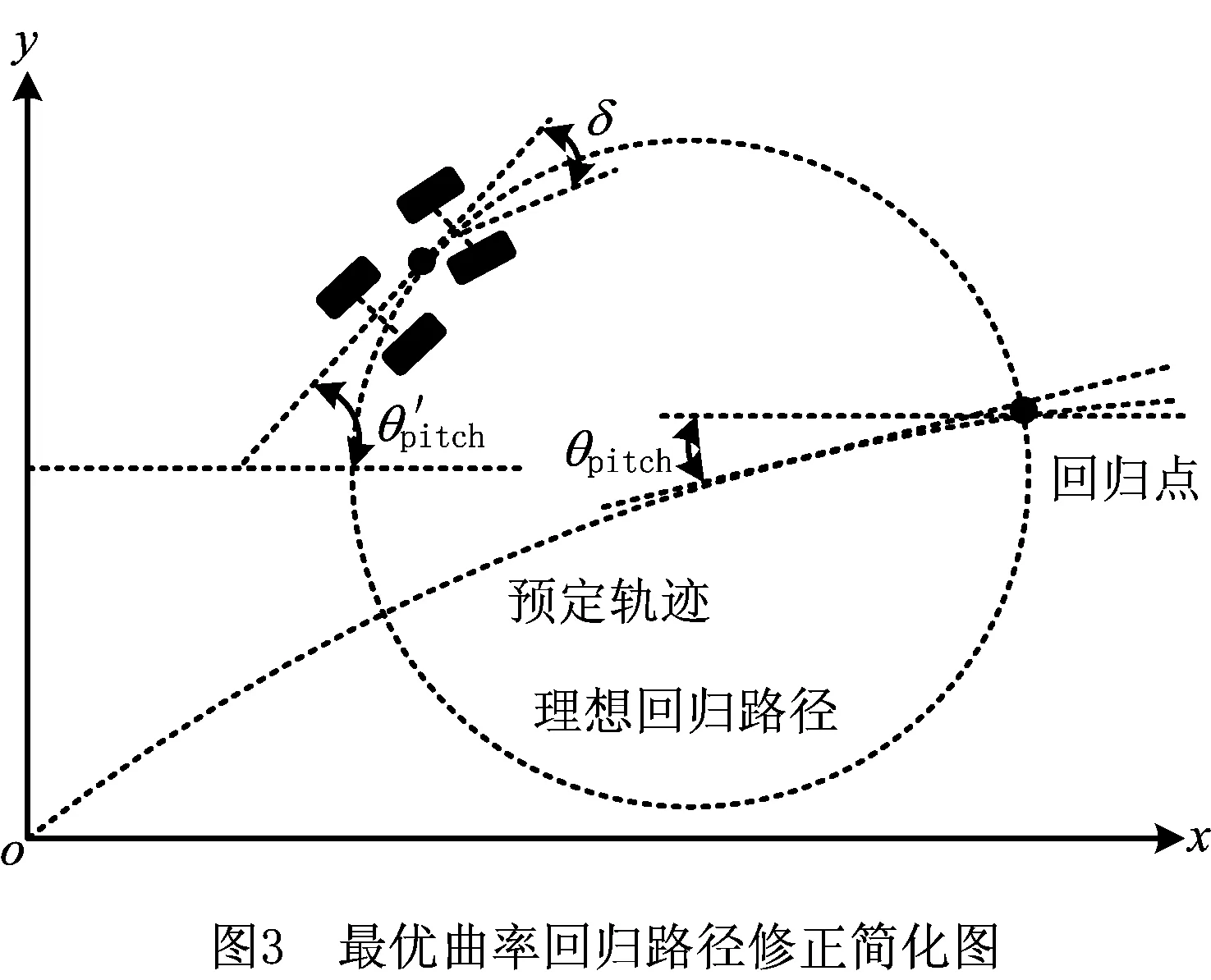
由于两圆等半径且相切，可以求出修正后的回归路径的半径。从图4可以看出，在△BCD中根据三角余弦定理可以求出DC：

(18)

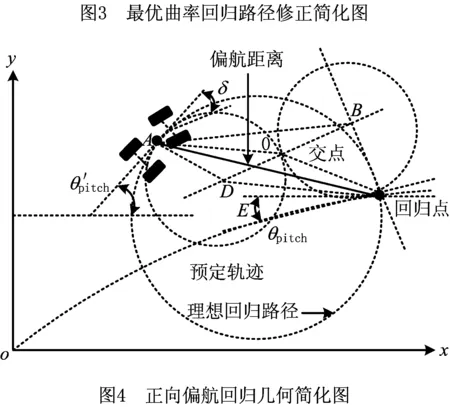
在△ACD中根据三角余弦定理可以求出DC，

(19)

联合式(18)和式(19)可得：

(20)

(21)

又知：

(22)

(23)

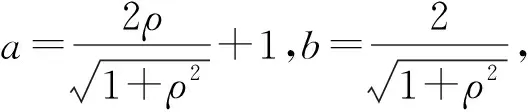
整理可得：

(24)

或

(25)

θpitch的大小根据前文凹凸性判断获取。由最终回归点车辆的位姿角可以看出，车辆的回归点只与车辆当前车速有关。

(26)

此时车速修正为：

(27)

对于负向偏航的简图如图5所示。

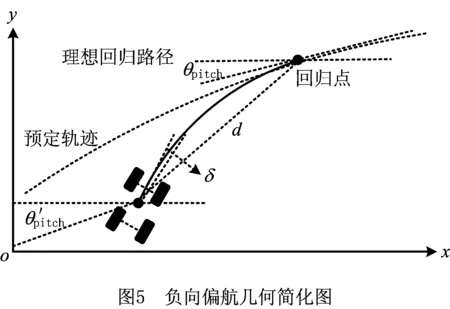
对于负向偏航而言，实线即为回归曲线。同样以Rrectify为半径，以车辆主轴方向为切点画轨迹圆，必须保证轨迹圆与预定轨迹相切，与路径的切点即为车辆回归点，回归点的位置唯一确定。

如图6所示，在△ABC中可以获取回归点的位置坐标为：

(28)

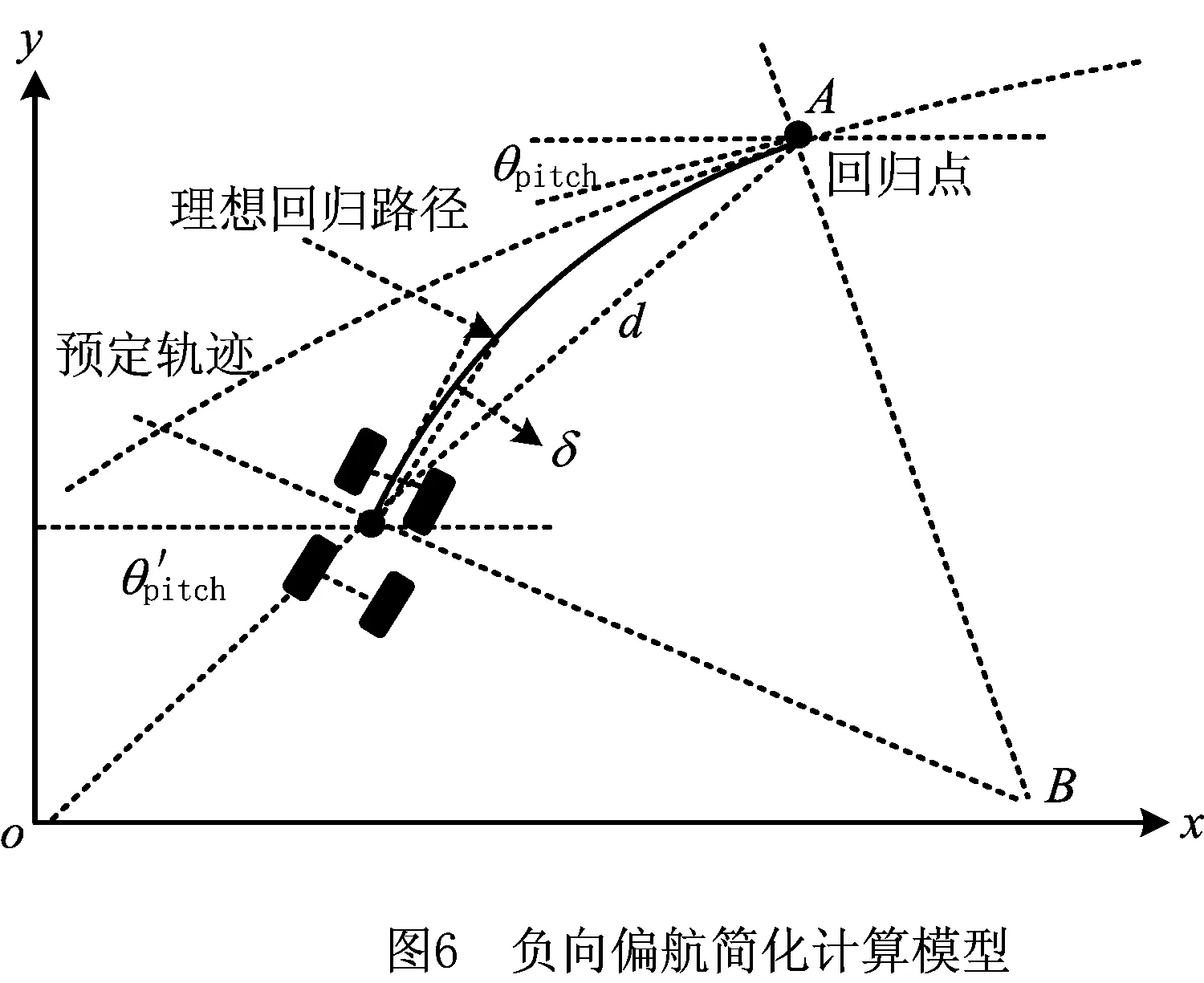
进一步整理得：

(29)

式(29)说明，对于负向偏航而言，回归点坐标同样只与当前位置的路径曲率或速度有关。

2 补偿转向角的计算

车辆转弯过程中，取内外车轮转角的均值为车辆转向角δ。根据两轴车辆的转向特性，且忽略车轮的弹性变形，可以求出转向角与路径曲率之间的关系：

(30)

由式(30)可以看出，轴距l为常数，因此车辆纠偏过程中，纠偏路径曲率与车辆转角之间存在函数关系。此时，车辆转向角

(31)

式中A、B分别为△ABC对应顶点的角。

对于正向偏航，车辆第一次转向角修正在A点，修正大小为

Δδ1=δ-δ0=arcsin

(32)

车辆第二次修正转向角在点o，此时其转向角变为-δ，则车辆转向角修正量为

Δδ2=-2δ=-2arcsin

(33)

车辆第三次修正转向角在点C，此时其转向角变为预定路径在C点的转向角，则车辆转向角修正量为：

δ3=δ′-(-2δ)=arctan

(34)

对于负向偏航，车辆转向角调整只需一次即可完成，其大小可以表示为：

(35)

3 速度跟踪控制模型

受路径曲率、车辆位姿角以及路面的附着条件影响，车辆在预定轨迹上行驶过程中的速度受到限制，各点速度不一样，因此必须实时控制车辆速度。

通过解耦计算得出的车辆转向曲线的各点曲率，可以得到车辆转向最大速度，保证车辆的实时性。

3.1 无偏航时速度跟踪数学模型

在行驶过程中，车辆要想跟随预定速度行驶就必须不断调整车辆驱动力，从而控制车辆加速度，达到缩小速度跟踪误差直至误差为零的目的。其数学表达式为：

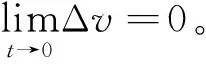
(36)

根据力矩计算公式：

(37)

可得

(38)

式中Ji为车轮的当量转动惯量(单位：kg·m2)。

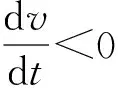
3.2 存在偏航误差时速度跟踪数学模型

为了保证车辆在回归点迅速进入跟踪状态，让车辆速度跟踪规划速度，且及时补偿速度差，对速度阈值和补偿值进行计算。当回归速度不等于规划速度时，车辆根据当前位姿角或转向角分配制动力矩或驱动力矩，在保证速度跟踪的同时保证车辆稳定性。回归点车辆速度可以根据回归曲率进行计算：

(39)

则回归点的速度差Δv=v(t)-v。速度差的出现表明制动系统和驱动系统需要补偿驱动力矩或制动力矩。

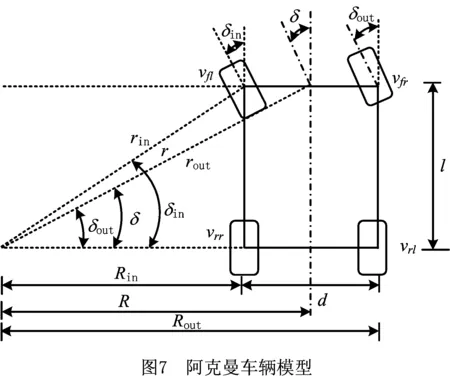
不论有无偏航，必须利用驱动和制动为车辆的速度进行补偿，且速度补偿与转向有关。为了计算出4个车轮的速度和转矩需求，利用阿克曼转向模型进一步说明。如图7所示，其中δm为δin为内侧车轮转角;δout为外侧车轮转角(单位：°);vfl、vfr、vrl、vrr分别为左前、右前、左后、右后车轮速度(单位：m/s);rin、rout分别为左前轮和右前轮的转弯半径(单位：m);Rin、Rout、R分别为左后轮和右后轮的转弯半径以及车身转弯半径(单位：m)。

针对图7，忽略车轮滑移滑转且轮胎始终保持与地面接触，轮胎侧向力与侧向变形成正比。根据车辆转向原理作运动学分析，以路径规划过程中所规划的速度和路径所规划的转向角为输入，计算得到车辆四轮的速度函数：

(40)

式(40)中速度vq和δ均为关于时间的函数。根据Δv的计算，4个车轮必须补偿的速度为：

(41)

车轮角速度差Δvi可以利用式(41)计算得到，根据车轮角度速度差可以计算出转矩输入。

(42)

此时，根据力矩计算公式可得：

(43)

(44)

其中：Fzi为车轮垂直载荷(单位：N)；mwheel为车轮质量，单位(kg)；ri为车轮内径(单位：m)。

由此可得：

(45)

3.3 力矩分配控制

四驱车辆具有4个独立可控的驱动装置，且4个轮毂电机可以降减矩或反转，从而达到减速的目的，因此为了保证自动驾驶车辆路径跟踪过程中的稳定性和安全性，必须对驱动力矩制定分配控制策略，从而保证驱动力矩迅速根据车辆指令做出反应。

车辆纵向需要根据速度变化需求不断改变驱动力矩。根据车辆目前参数识别利用传感器获取车辆当前车速、转向角、横摆角速度、质心侧偏角等参数，利用所规划的路径计算下一刷新时间段的转向角和目标车速。

实际车辆运行时，由于路面附着条件、侧风等环境条件的影响，车辆会偏离由理想二自由度车辆模型获取的理想质心侧偏角βd和理想横摆角速γd，必须给车辆添加ΔM控制车辆的不稳定性。期望横摆力矩ΔM利用Fuzzy-PID控制器6进行控制，控制流程如图8所示。

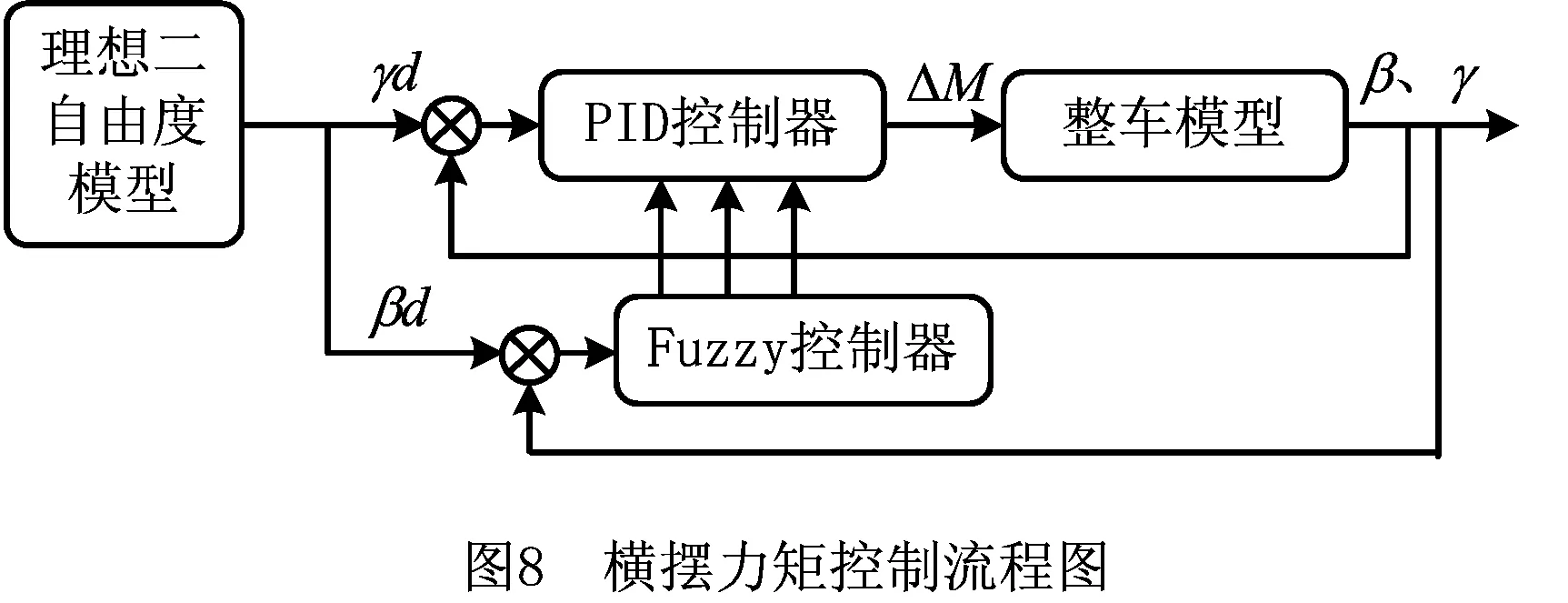
参考文献[10]设计Fuzzy-PID控制器，如图9所示。将质心侧偏角差与质心侧偏角变化率的变化范围定义为[-5,5]。[-5,5]为模糊论域，将论域分化成负大、负中、负小、零、正小、正中、正大7个模糊子集，分别为NB,NM,NS,ZO,PS,PM,PB。假定质心侧偏角差与质心侧偏角变化率以及kp、ki、kd三个参数均服从高斯分布，设计Fuzzy-PID控制器。

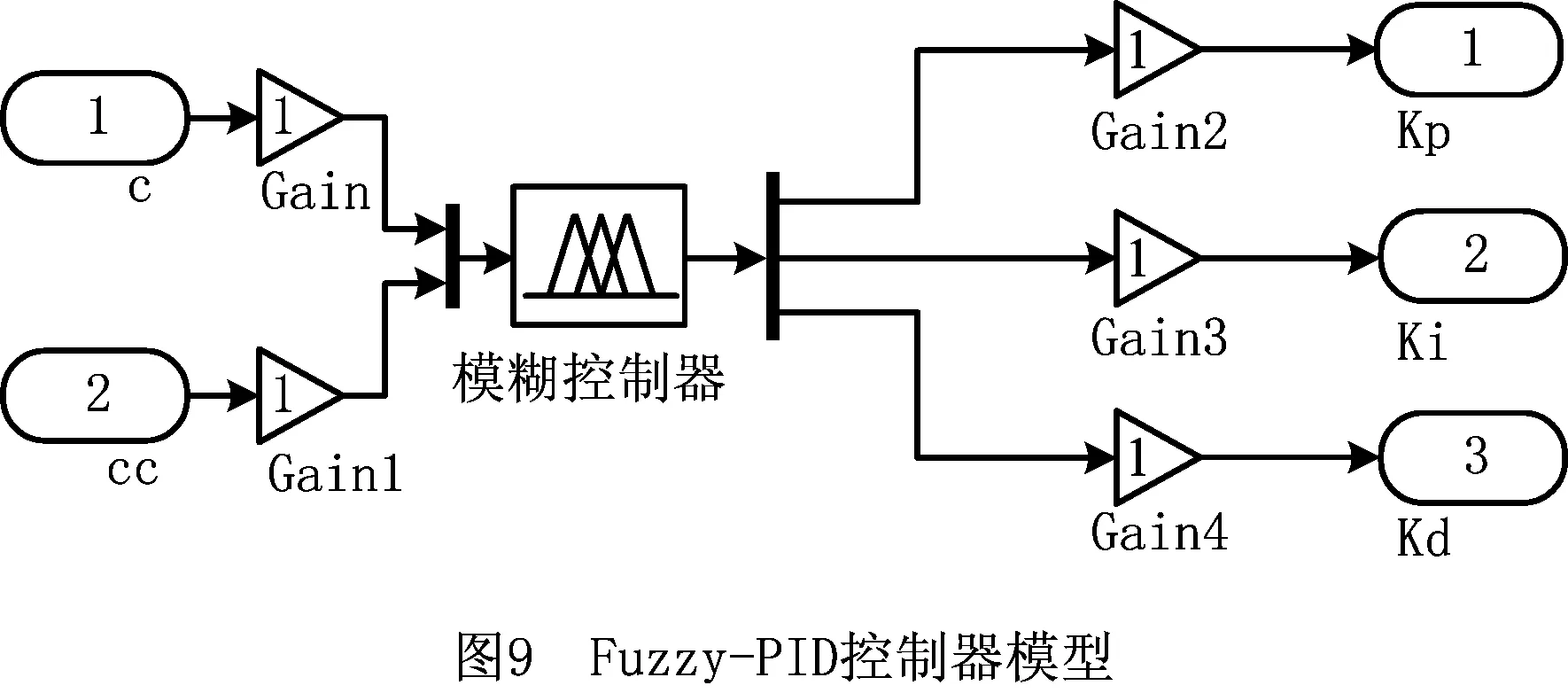
轮毂电机的转矩分配问题不存在固定解，参考文献[11]对转矩分配作如下规定：

(1)4个车轮的驱动力矩与其对应的垂直载荷有关。

(2)采用十字等配的方式分配驱动力矩，一边力矩增加，相应的另外一边减小，其数学表达式为：

(46)

4 偏航控制仿真试验

利用MATLAB/Simulink对路径规划设计和轨迹跟踪控制设计搭建模型，并进行离线仿真验证，验证所设计模型。

根据路径规划所获取的曲率计算车辆目标转角和转速；利用偏航计算计算出补偿转角和规划车速。利用规划转向角、补偿车辆转向角和规划车速获取目标转矩和横摆角速度，并利用转矩分配算法对4个车轮的转矩进行分配，根据速度需求选取执行机构，最终将分配的力矩输入到整车模型进行验证。流程图如图10所示。

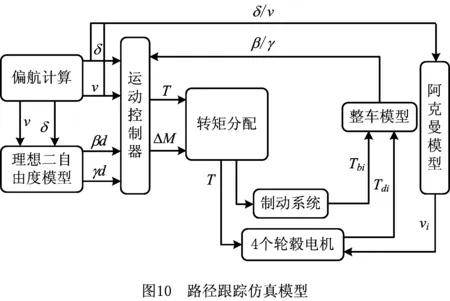
4.1 数学模型

为了在MATLAB/simulink中建立仿真模型，必须分别针对不同模块建立数学模型，包括规划路径计算模块、轮胎模型、整车模型、二自由度模型。

4.1.1 Dugoff轮胎模型

根据Dugoff模型的定义，轮胎纵向力和侧向力与轮胎刚度、滑移率等参数有关，其表达式为[12-13]：

(47)

式中：

(48)

(49)

式中：i=fl，fr，rl，rr分别表示左前轮，右前轮，左后轮，右后轮；Cxi、Cyi为轮胎纵向刚度和侧偏刚度(单位：N/m)；si为轮胎滑移率；ψi为轮胎动态参数；μ为路面摩擦系数；αi为车轮侧偏角(单位：rad)；Fzi为轮胎法向载荷(单位：N)。

车辆运动过程中，总是存在纵向和侧向的滑移或滑转，其定义为：

(50)

式中Ω为车轮滚动速度(单位：rad/s)。

4.1.2 七自由度整车模型的搭建

车辆七自由度简化模型如图11所示。

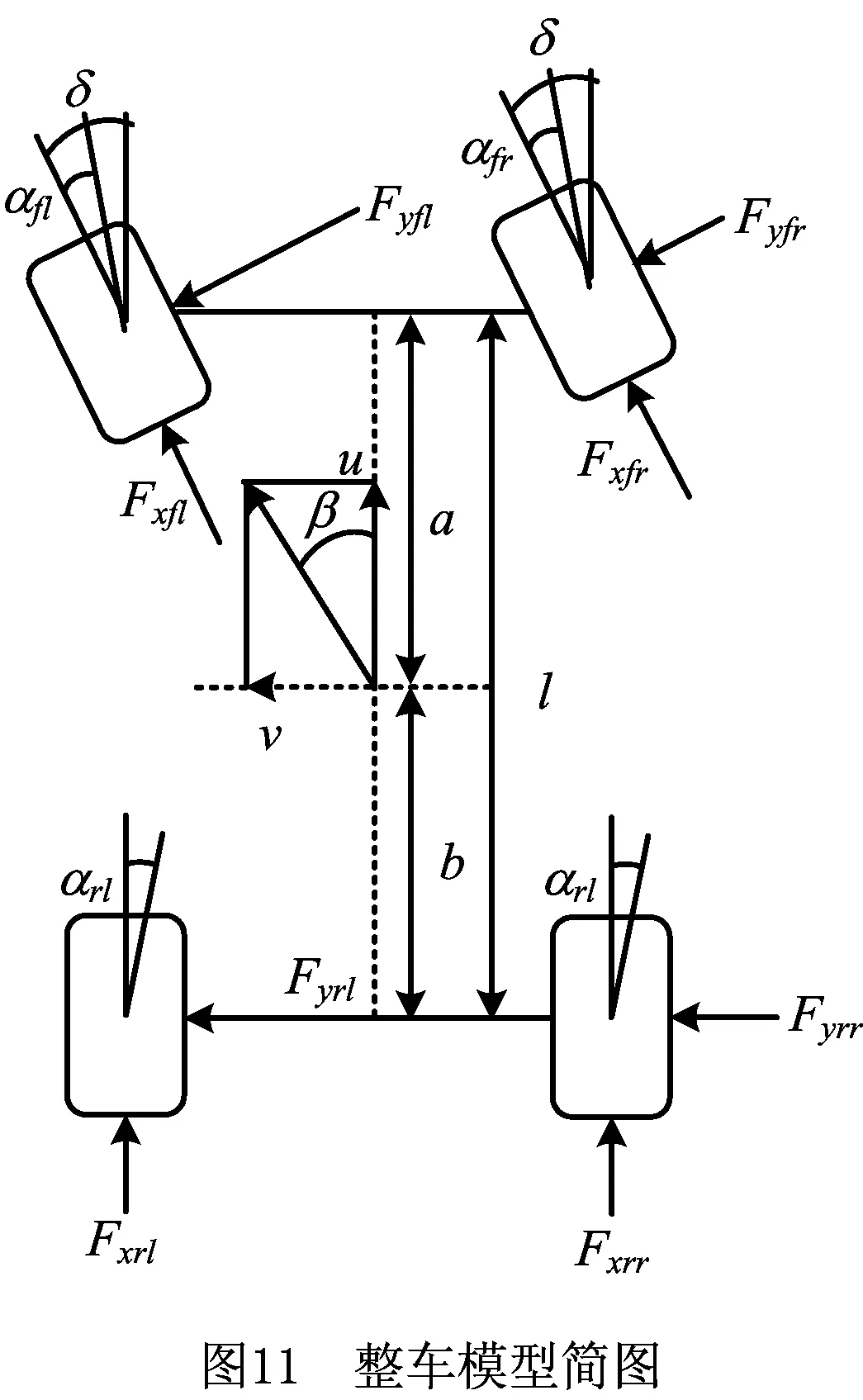
纵向力平衡方程：

(Fyfl+Fyfr)sinδ+Fxrl+Fxrr。

(51)

侧向力平衡方程：

(Fyfl+Fyfr)cosδ+Fyrl+Fyrr。

(52)

绕Z轴力矩平衡方程：

cosδ]a+[(Fxfr-Fxfl)cosδ+

(53)

4个车轮的力矩平衡方程：

(54)

上述方程中，β为质心侧偏角(单位：rad)；Γ为横摆角速度(单位：rad/s)；Fxi、Fyi、Fzi分别为轮胎纵向力、侧向力、垂向力(单位：N)；Ms为悬挂质量(单位：kg)；a、b分别为前后轴到质心的距离(单位：m)；l=a+b为前后轴距(单位：m)；Bf为前轴轮距(单位：m)；Br为后轴轮距(单位：m)；Iz为整车绕Z轴的转动惯量(单位：kg·m2)；Hg为质心到地面的距离(单位：m)；Itw为轮胎转动惯量(单位：kg·m2)。

各轮胎垂向载荷计算公式为：

(55)

各轮胎侧偏角计算公式为：

(56)

各车轮滑移率的计算：

(57)

在MATLAB/Simulink中搭建七自由度整车模型。

4.2 理想二自由度模型

二自由度二轮转向理想模型用来描述操纵稳定性，常用作参照模型。为保证所建立的七自由度整车仿真模型具有很好的参照模型和跟踪性能，建立以下理想二自由度参考模型：

(58)

为便于建模，将二自由度理想参考模型转换成如下的状态空间形式：

(59)

根据二自由度车辆模型可求得理想质心侧偏角βd和理想横摆角速γd。

4.3 路径跟踪仿真

为了保证检验前文所建立的各个模块的准确性和相关度，利用数学模型在MATLAB/Simulink中搭建离线仿真模型，如图12所示。为了观测轨迹跟踪情况，验证各模块设计的有效性，针对直线路径工况、圆形路径工况以及随机路径工况进行仿真验证，仿真参数如表1所示。

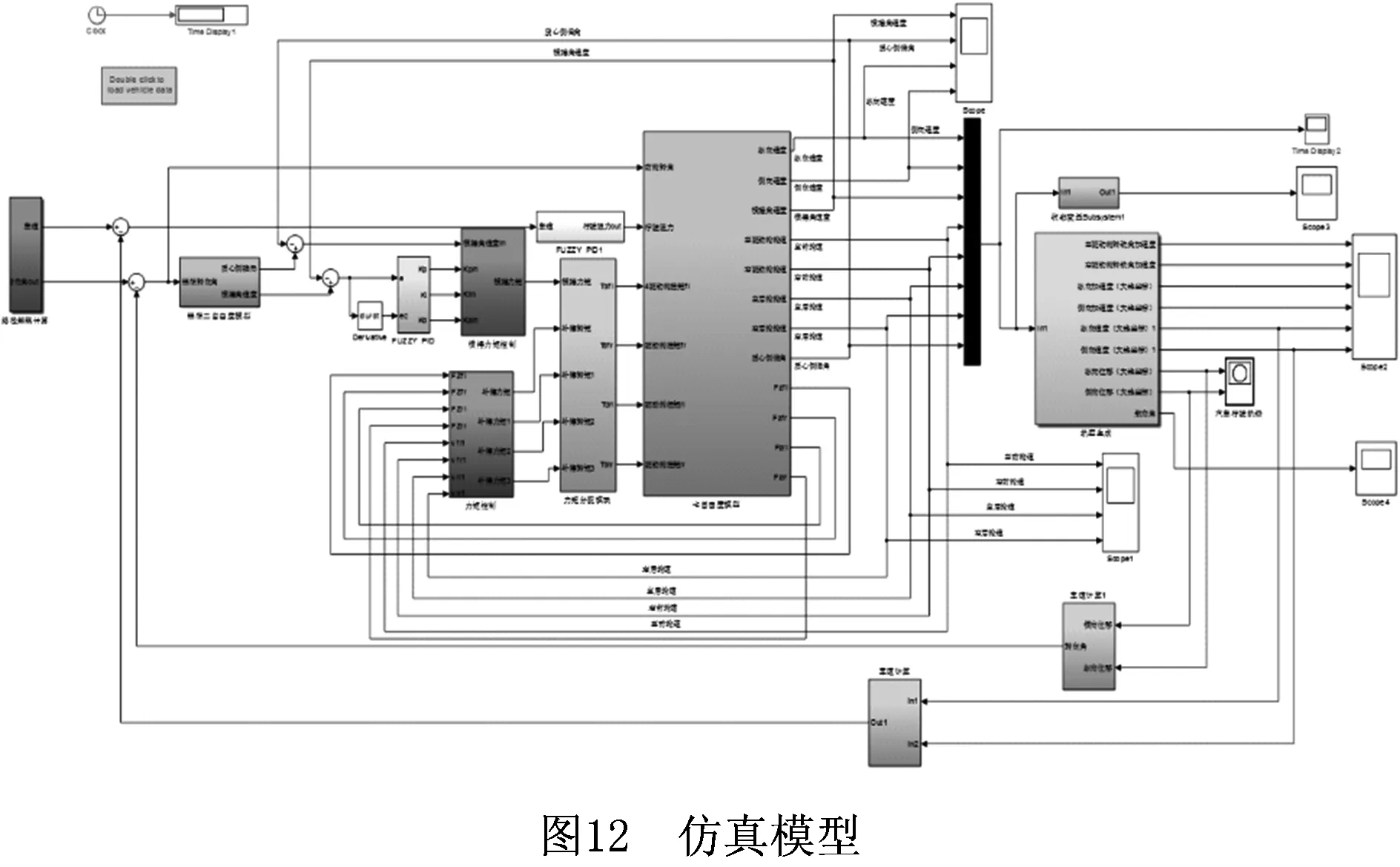
表1 仿真参数表

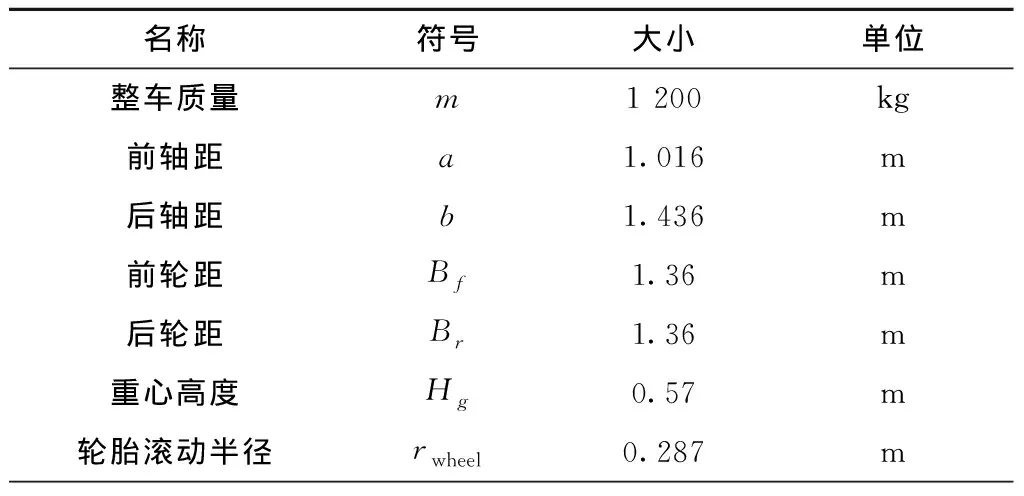
m1 200kga1.016mb1.436mBf1.36mBr1.36mHg0.57mrwheel0.287m

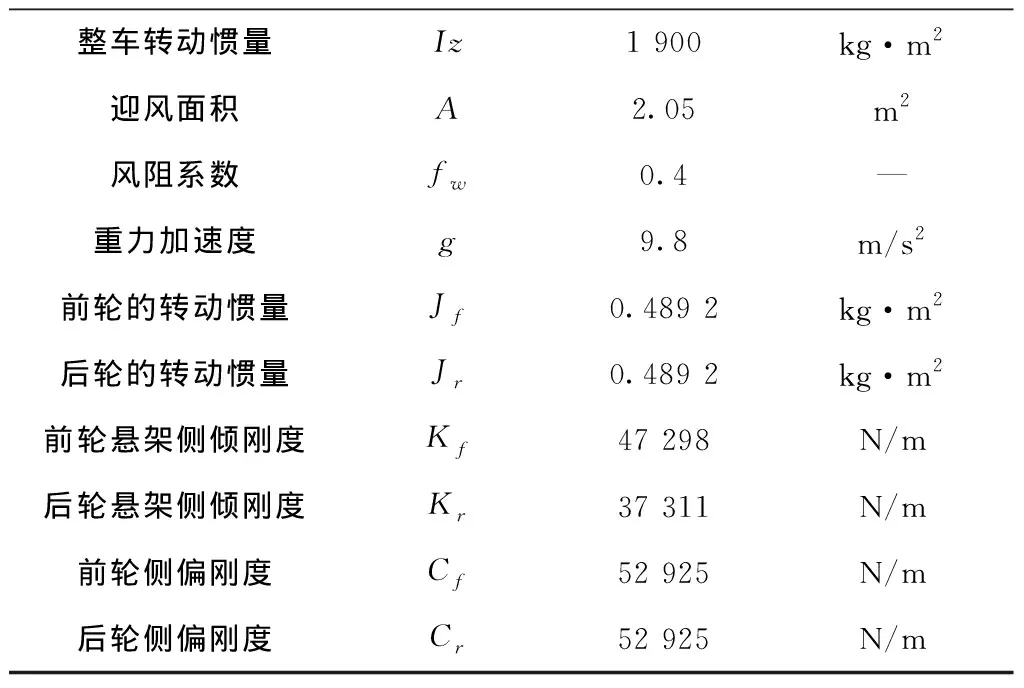
续表1

4.3.1 直线路径工况

直线路径是车辆最简单的行驶路径，车辆在直线路径上能否保证直线行驶与车辆的操纵稳定性相关，自动驾驶车辆在直线路径上能否直线行驶还与路径跟踪控制性能相关。

在该工况下，设定车辆初始速度为80 km/h，路面附着系数为0.8。预定轨迹即车辆规划路径为一条直线，如图13，车辆初始位置为(45,-80)。设置仿真时间为20 s，仿真步长为0.1 s，仿真结果如图13和图14所示。

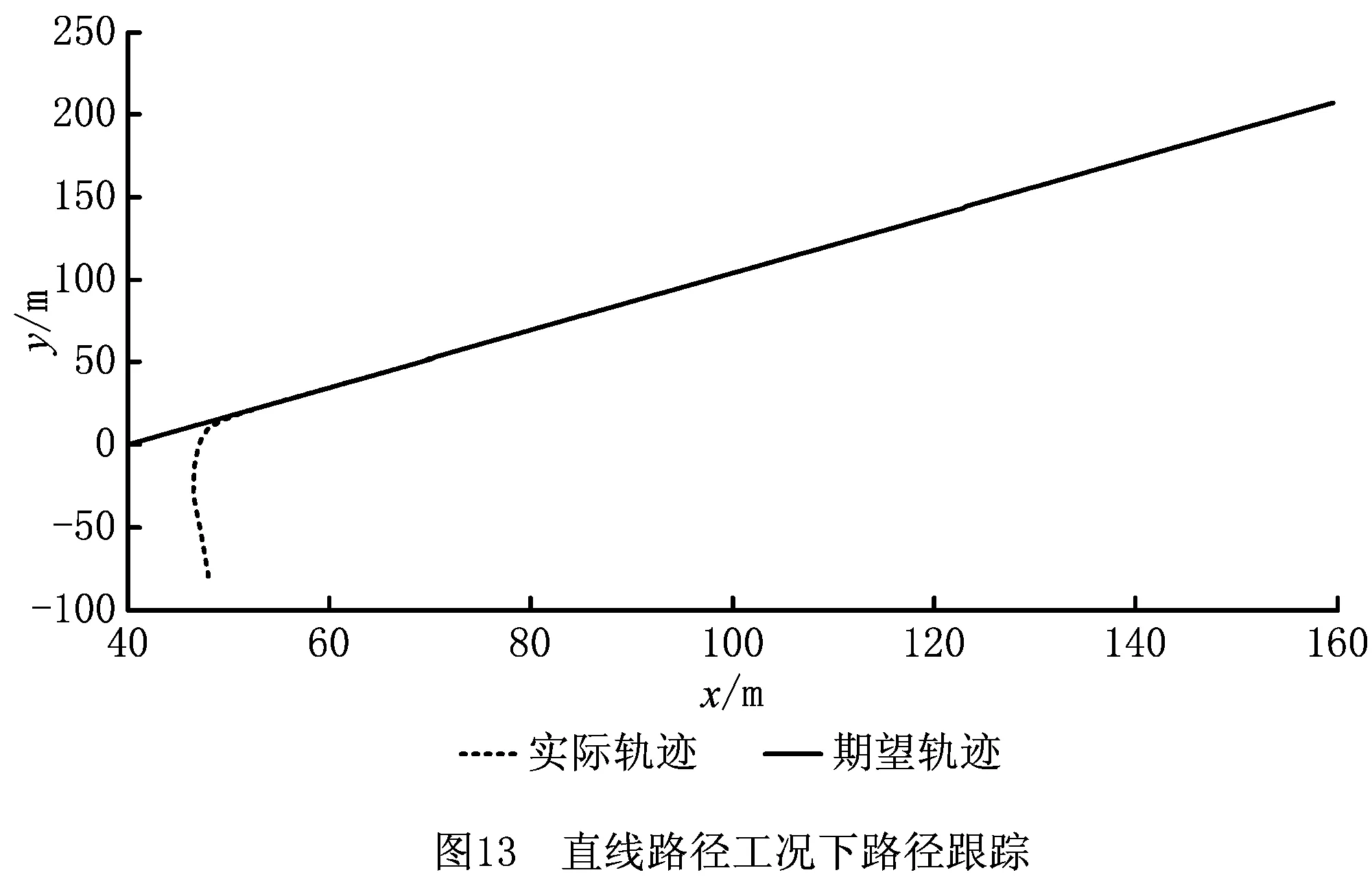
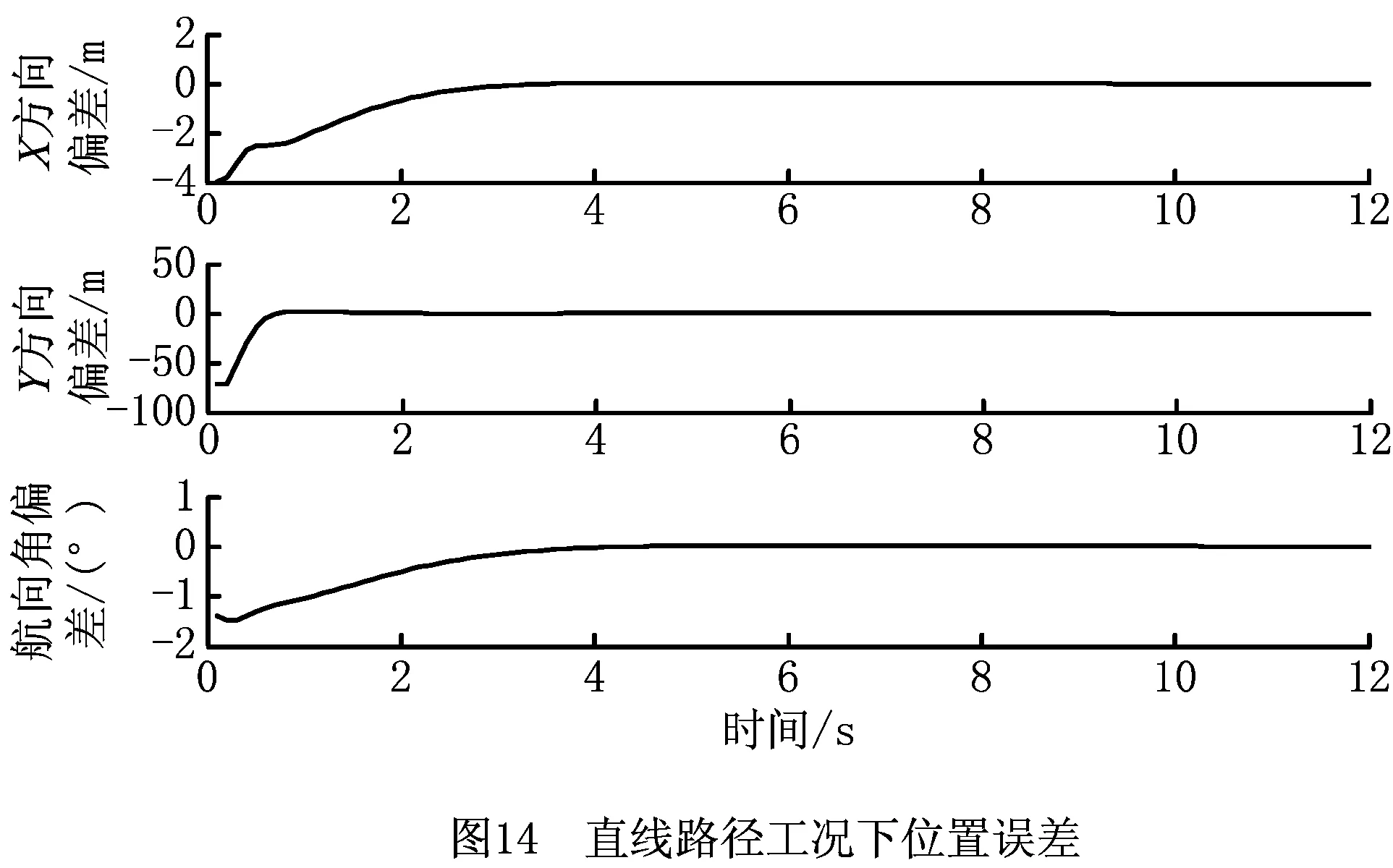
由图13可以看出，车辆初始位置严重偏离规划路径，车辆迅速回归，最终与期望轨迹重合。从图14可以看出，随着车辆运行，车辆所在位置的坐标误差迅速减小，y坐标误差减小幅度最大，最终位姿角以及位置坐标误差在4 s后缩小为零。

4.3.2 圆形路径工况

在该工况下，设定车辆初始速度为80 km/h，路面附着系数为0.8。预定轨迹是半径为100 m的规则圆形轨迹，如图15。车辆初始位置为(-45,120)。设置仿真时间为50 s，仿真步长为0.1 s，仿真结果如图15～图18所示。

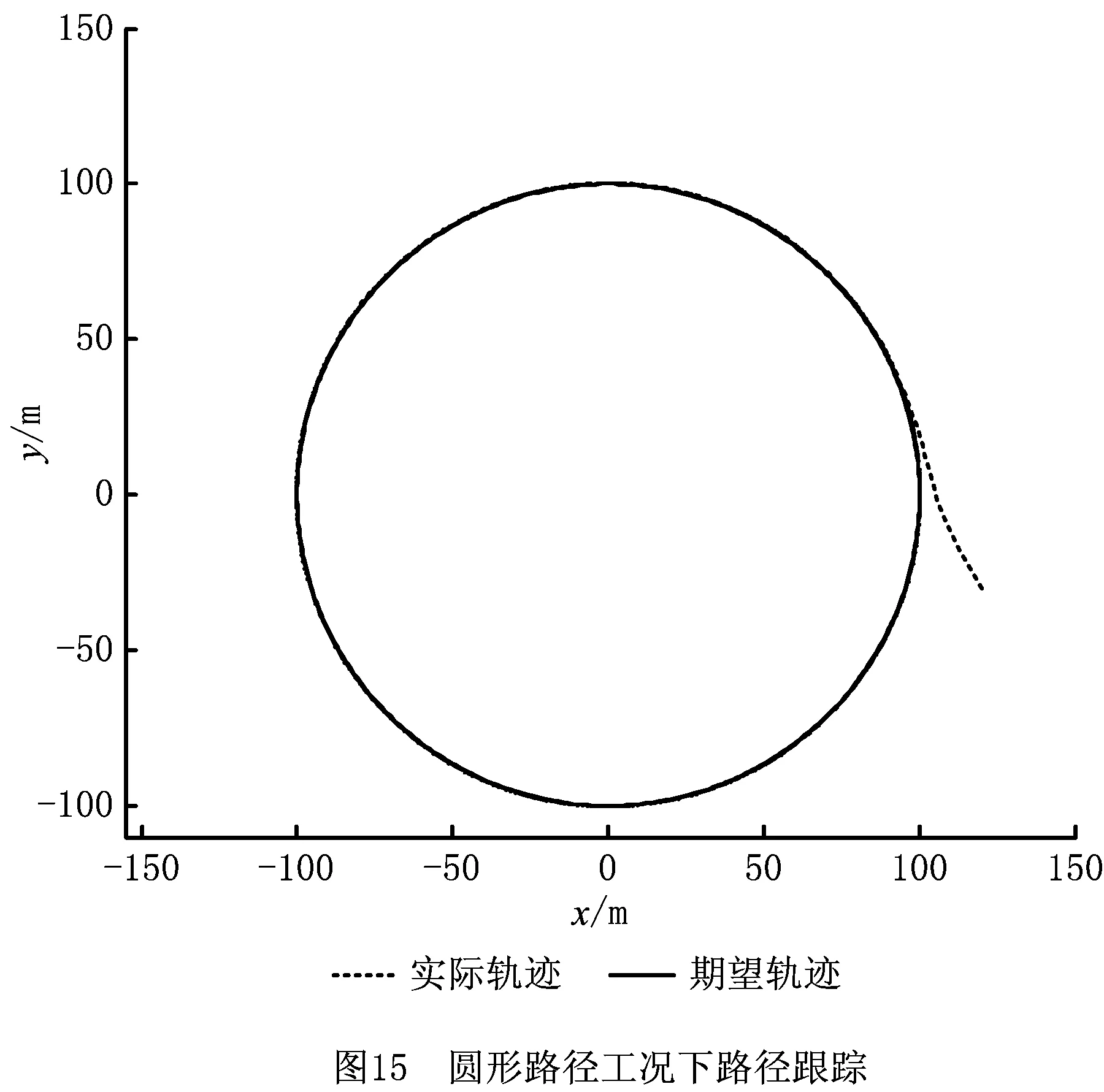
由图15可以看出，车辆初始位置与规划路径偏离较远，随着车辆运行，车辆迅速回归，最终与期望轨迹重合，并稳定性作圆周轨迹运动。

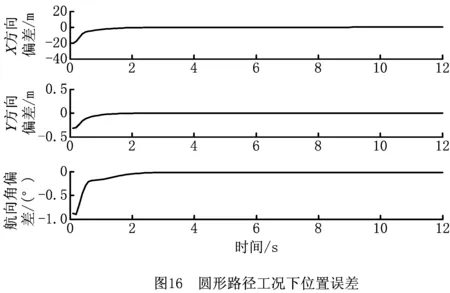
从图16可以看出，随着车辆运行，车辆所在位置的坐标误差迅速减小，位姿角误差减小幅度最大，最终位姿角以及位置坐标误差在3 s后缩小为零。

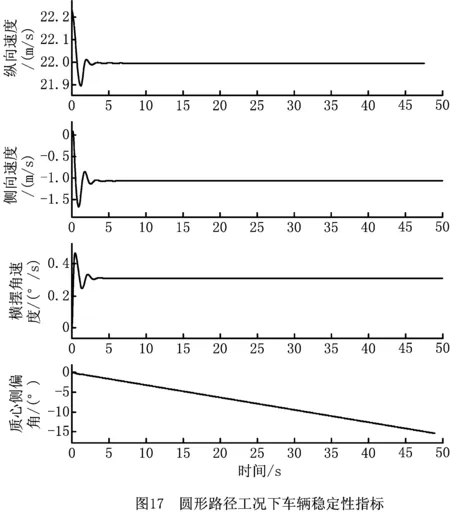
从图17可以看出，随着车辆的运行，车辆的横摆角速度、横向速度和侧向速度均可快速达到稳定，从而表明对于圆形路径的轨迹跟踪，车辆可以稳定运行，且稳定时间较短。

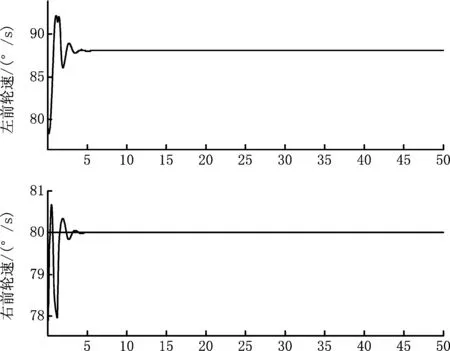
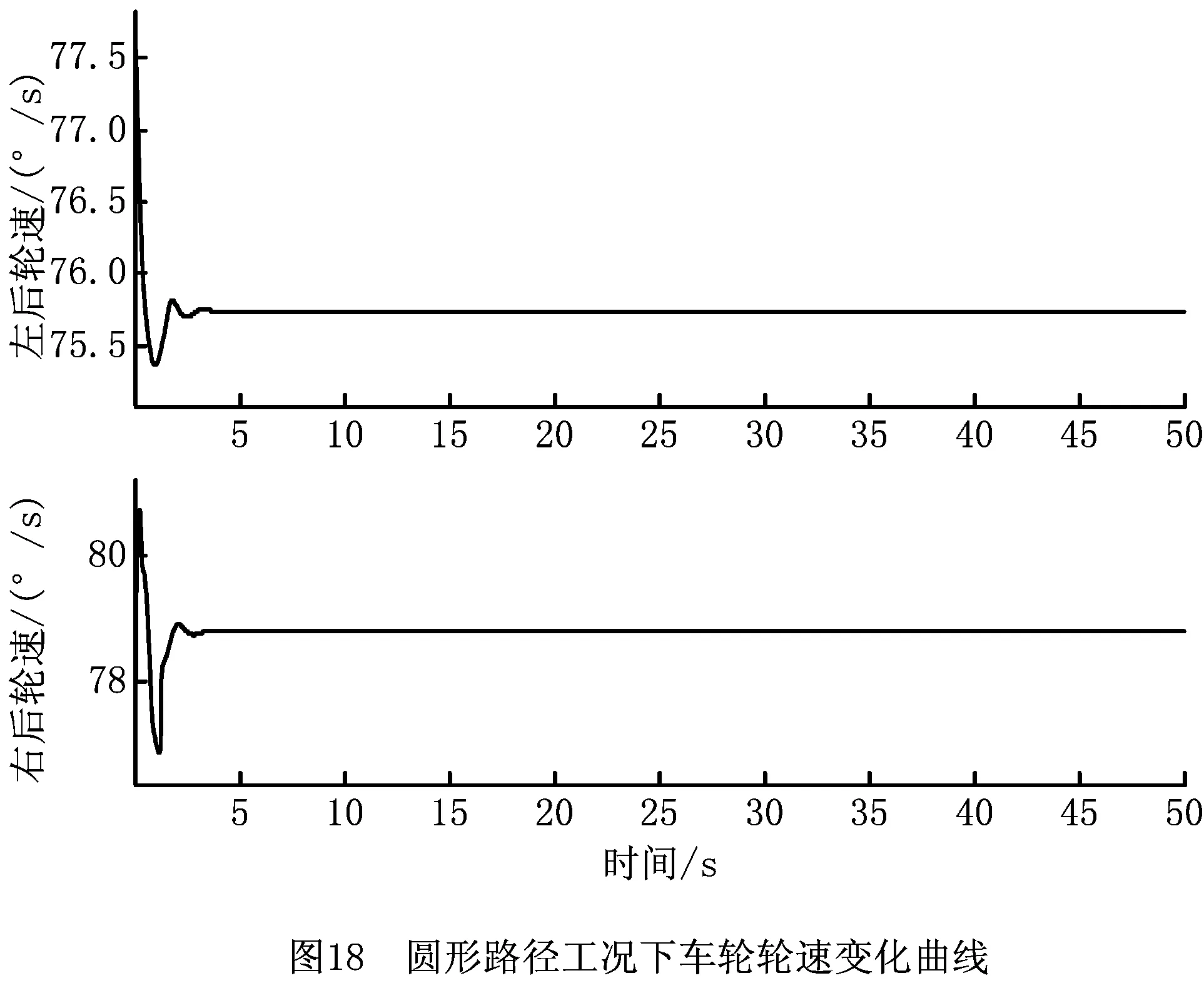
从图18可以看出，随着车辆的运行，车辆的4个车轮的轮速均可迅速达到稳定。2 s前由于车辆不断调整位姿以及转向，因此4个轮速并未达到稳定，车辆通过制动和驱动不断调整轮速，最终达到基本稳定状态。

4.3.3 随机路径工况

随机路径工况最接近车辆实际的行驶路径，车辆在随机路径工况上能否稳定行驶与车辆的操纵稳定性相关，自动驾驶车辆在随机路径上能否直线行驶还与路径跟踪控制性能相关。

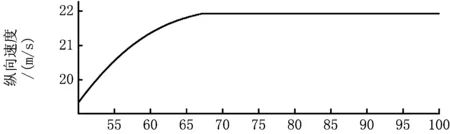
在该工况下，设定车辆初始速度为80 km/h，路面附着系数为0.8。预定轨迹即车辆规划路径为随机螺旋线，如图19所示，车辆初始位置为(180,120)。设置仿真时间为100 s，仿真步长为0.2 s，仿真结果如图19～图22所示。

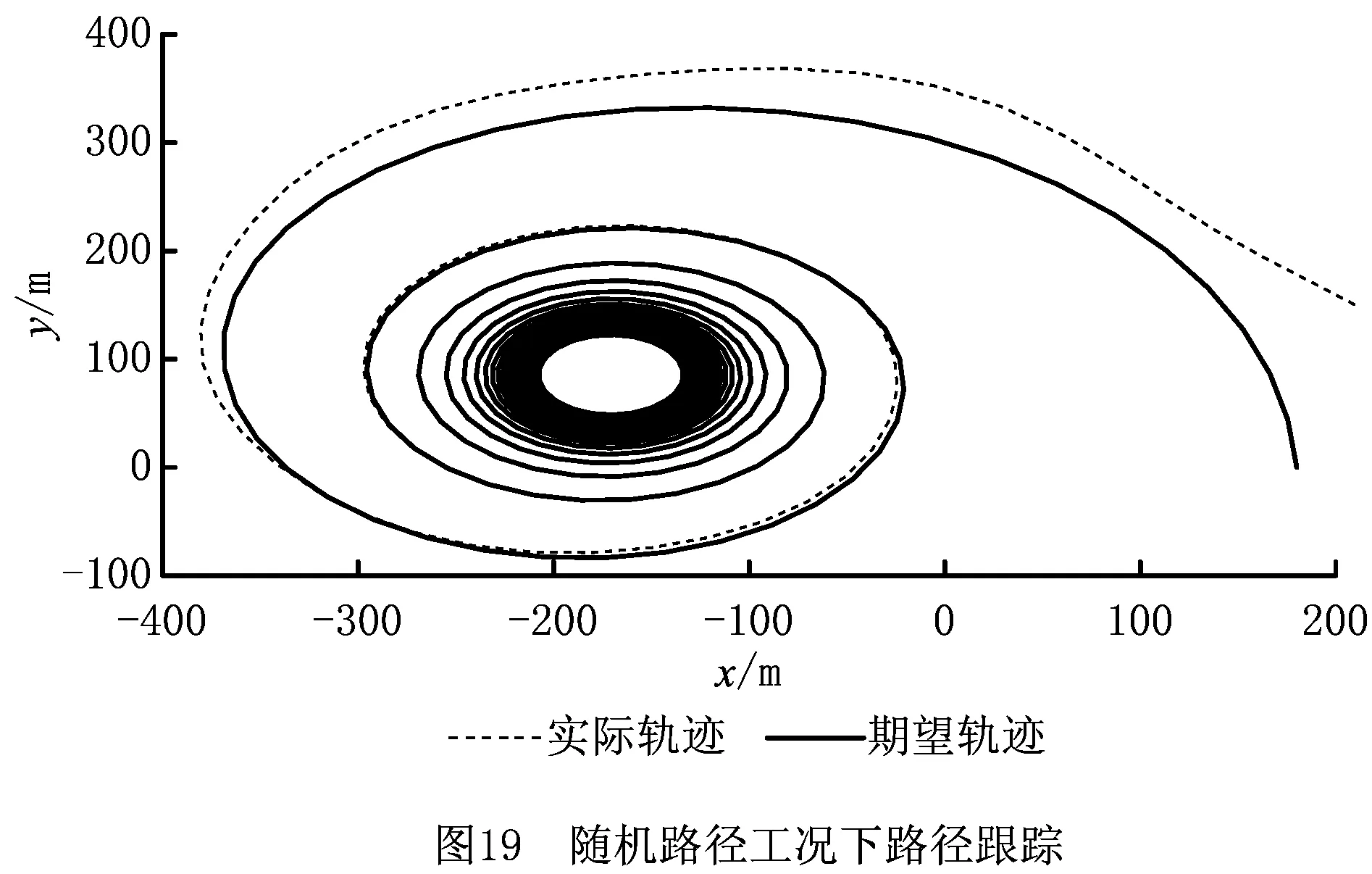
从图19可以看出，车辆初始位置偏离规划路径，车辆逐渐回归，最终与期望轨迹基本重合。从图20可以看出，随着车辆运行，车辆所在位置的坐标误差迅速减小，y坐标误差减小幅度最大，最终位姿角以及位置坐标误差在10 s后逐渐稳定。

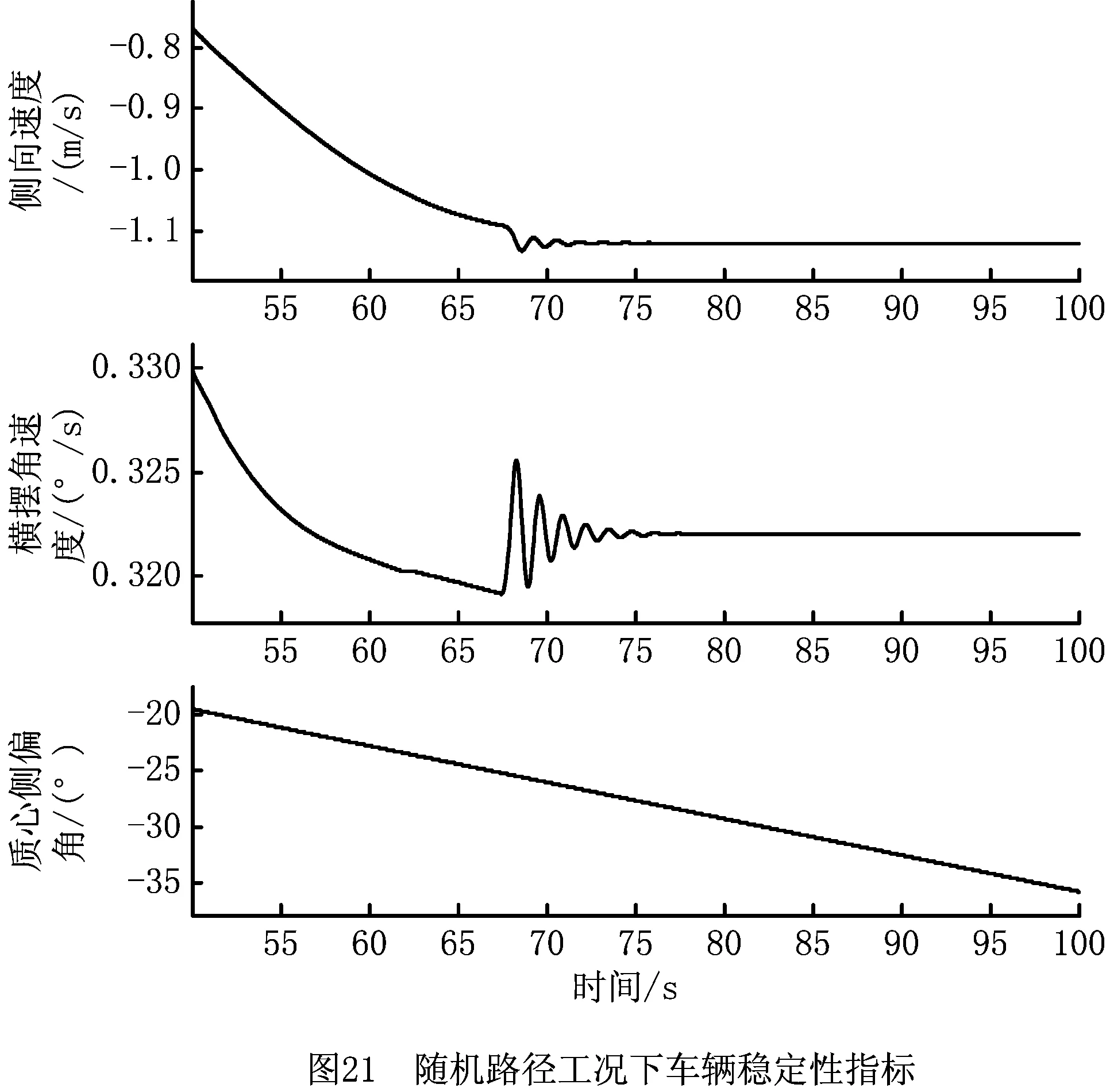
由图21可以看出，随着车辆的运行，车辆的质心侧偏角、横摆角速度、横向速度和侧向速度均可快速达到稳定，表明对于随机路径的轨迹跟踪，车辆可以较稳定地运行。

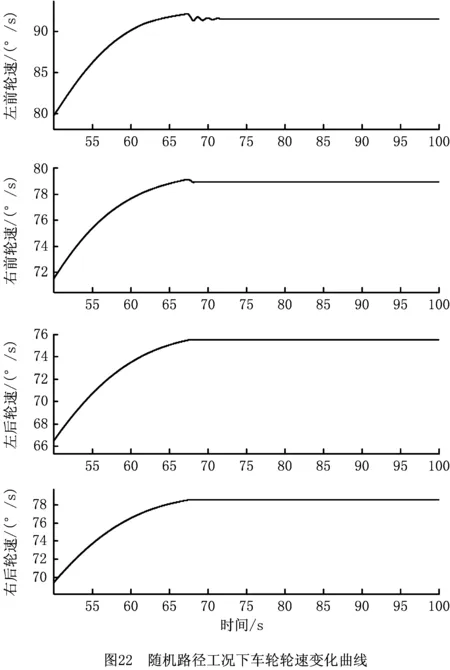
由图22可以看出，随着车辆的运行，车辆的4个车轮的轮速均可在75 s左右达到稳定。由于车辆不断调整位姿以及转向，加之路径的不规律性，4个轮速无法迅速达到稳定，车辆通过制动和驱动不断调整轮速，最终达到基本稳定状态。

5 结束语

偏航控制是路径跟踪过程中出现的复杂非线性控制问题，基于单点预瞄理论的控制方法未考虑回归点车辆位姿角和预定轨迹回归点角度重合问题，即车辆回归点的姿态角与规划轨迹的方向角度不重合，使得车辆需要多次纠正才能回到预定轨迹。本文考虑回归航向角重合度的问题，根据路轨迹曲线的凹凸特性，提出一种圆弧回归方法，计算了转向角补偿量，并充分考虑回归实时性和安全性，计算了车辆最大回归速度和速度补偿量。建立了偏航数学模型、速度跟踪模型、整车仿真模型，针对直线路径工况、圆形路径工况和随机路径工况进行了仿真，结果表明：

(1)3种工况条件下，车辆初始位置严重偏离规划路径，车辆可以迅速回归，最终与期望轨迹重合，车辆在3种工况下可分别在4 s、3 s、10 s使得位置误差和航向角误差达到稳定状态，其中直线路径工况和圆形路径工况位置误差都可以缩小为零，随机路径工况位姿角误差可以和位置误差达到稳定状态。

(2)随机路径工况条件下，车辆的质心侧偏角、横摆角速度、横向速度和侧向速度快速减小，但均存在波动，表明所设计的轨迹跟踪方法对于复杂路径还需要进一步研究和优化。

未来将把智能控制算法与所设计的路径偏航控制方法结合起来，提高车辆轨迹跟踪控制器的鲁棒性和实时性。