基于近似动态规划的模具项目调度

王小明，陈庆新，毛 宁

(广东工业大学 广东省计算机集成制造重点实验室，广东 广州 510006)

0 引言

项目管理协会(Project Management Institute, PMI)将项目定义为：“为创造独特的产品、服务或成果而进行的临时性工作”。模具设计和制造具有典型的项目特征，因此模具企业普遍采用项目管理技术和方法进行生产管理。在工程实际中，一个中等规模的模具企业往往同时承担几十上百个共享和竞争企业有限资源的项目。由于存在复杂的任务紧前约束和资源耦合，加之部分任务的实际工期难以准确估计，使得模具项目调度问题的求解难度极大。

在过去几十年，国内外学者对资源受限项目调度问题(Resource-Constrained Project Scheduling Problem, RCPSP)开展了广泛深入的研究，提出了大量建模和求解方法。然而，大部分研究是面向确定性环境下的RCPSP，如文献[1-2]。相比之下，随机环境下(任务工期或资源可用量不确定)的RCPSP在过去十几年才逐步受到关注。随机RCPSP的解并非确定的任务开工时间，而是一种调度策略，即系统状态和决策行动之间的映射函数。从文献[3]开始，马尔科夫决策过程(Markov Decision Processes，MDPs)成为随机RCPSP的通用建模方法，随机动态规划(Stochastic Dynamic Programming，SDP)则是求解其最优策略的基本方法。当任务工期服从负指数分布时，可直接采用MDPs构建对应随机RCPSP的决策模型，其决策目标通常是使得项目周期期望最小[4-6]或项目净现值期望最大[7-10]。当任务工期服从一般分布时，可先利用相型分布进行近似，再采用MDPs建模求解[7,11]。与耗费大量计算资源求解动态最优策略相比，部分学者更倾向于采用静态策略高效求解次优解[12-13]。更多关于随机RCPSP的研究见综述文献[14-19]。尽管资源受限多项目调度问题(Resource-Constrained Multi-Project Scheduling Problem, RCMPSP)可以通过项目网络合并的方式转化成一个虚拟的大项目，但是其决策目标通常使得项目总加权拖期成本或项目平均拖期成本最小，因而所采用的调度方法与RCPSP不同。

RCMPSP是一个NP难问题，无法高效地求解出最优解，现有研究大多是构建近似算法或策略。其中，启发式规则因其简单高效而被广泛研究并应用于RCMPSP[20-26]。其他一些能够近似求解RCMPSP的方法还包括遗传算法[27-28]、多智能体系统[29-30]、组合拍卖[31]等。随机RCMPSP比确定性RCMPSP要复杂得多，相应的研究也更少。对于这种复杂问题，文献[32]提出一种分层式项目计划和控制体系，为随机环境下选择合理的多项目计划方法提供了指导。与随机RCPSP研究相类似，MDPs理论在近年来也被逐步应用于随机RCMPSP中。尽管MDPs理论能够准确描述随机RCMPSP，但传统SDP方法在求解最优策略时需要完全枚举状态和行动空间，极容易面临维数灾。因此，现有基于MDPs的随机RCMPSP研究都将精力集中于构建高效近似方法。例如，文献[33]在采用MDPs理论构建考虑任务可能失败的随机RCMPSP后，提出采用状态仿真取样的方法近似求解。文献[34]在采用MDPs理论构建考虑资源可用量不确定下的随机RCMPSP后，提出采用多规则组合来限制可选行动空间。此外，近似动态规划(Approximate Dynamic Programming, ADP)方法通过值函数近似来避免状态空间完全枚举，能够有效应对维数灾[35]。基于ADP，文献[36-37]研究了考虑新项目随机到达的RCMPSP。另有一些学者将面向确定性RCMPSP的启发式规则也视为一种随机调度策略，用于近似求解随机RCMPSP[38-40]。总体来说，启发式规则计算效率最高，但是优化效果往往较差；ADP方法的优化效果取决于值函数的近似误差，而复杂随机优化问题的值函数往往很难准确近似。

鉴于上述工程需求和理论研究现状，本文将研究部分任务工期服从已知离散分布下的模具项目调度问题，探索基于SDP的精确方法以及基于优先规则、遗传算法、ADP的近似方法。

1 问题描述

模具项目调度问题由一个并行项目集φ={1,2,…,n}和一个可更新资源集R={1,2,…,K}构成。项目i∈φ对应价值vi，拖期惩罚系数bi，投放时间ei以及交货期Di，并以单代号网络图(Activity-On-Node，AON)G(Ni,Ai)表示。其中：Ni={ni1,ni2,…,nimi}表示项目i∈φ的任务集合，Ai表示任务间的紧前约束关系，αi=vibi表示该项目的拖期边际成本。若项目i∈φ的实际完工时间为Fi，则其加权拖期成本TCi=αimax{Fi-Di,0}。

在上述问题环境下，项目管理人员需要对项目任务进行动态调度决策，以使所有项目完工时的总加权拖期成本期望最小。

2 数学模型

MDPs是一种用于随机环境下的序贯决策问题建模和求解的方法[41]。如前所述，该理论近年来已经被广泛应用于随机资源受限项目调度问题[4,7-11,34]，但其缺点在于仅能够精确求解小规模问题。由于本文考虑任务工期服从离散概率分布，下面将基于离散时间MDPs理论构建模具项目调度决策模型。

2.1 MDPs建模

离散时间MDPs可由五元组{T,X,A,p(x′|x,a),c(x′|x,a)}表达[43]，定义各要素如下：

(1)决策时刻集T除初始时刻外，决策者只能在有任务完工的时刻进行新任务开工决策。由于不需要关注相邻决策之间的时间间隔，可将决策事件视为等周期发生。定义系统决策时刻集T={1,2,…,Z}，其中Z表示令所有任务开工所需决策次数。

(2)状态集X为了获得合理的任务开工决策，决策者需要了解当前各项目进度状态以及资源可用信息。由于在制任务不仅部分描述了项目进度，还间接表达了可用资源信息，该信息必然包含在系统状态中。令Gx={(j1,s1),(j2,s2),…,(jn,sn)}表示状态x下的在制任务集，其中：jl∈Gx表示第l个在制任务，sl∈表示其开工时间，n表示该状态下的在制任务总数。为了完整表达项目进度信息，还需要在状态中加入系统当前时间tx，以及已完工任务集Fx，如下式所示：

x=[tx,Fx,Gx]T。

(1)

初始时刻，所有任务均未开工，系统初始状态x0=[0,∅,∅]T。当所有任务都完工时，系统将永久停留在一个最终状态。采取不同调度策略得到的最终状态具有相同的完工任务集和在制任务集，但到达最终状态的时间可能不同，因此系统将存在多个不同的最终状态。

(3)行动集A给定任意状态x∈X，均有一个可选行动集Ax⊂A与之对应。每种可选行动a∈Ax表示一种满足任务紧前约束和资源约束的任务开工组合。若在状态x∈X下没有任务满足开工条件，则Ax=∅将成为一种特殊的行动。

(5)成本函数c(x′|x,a) 0≤c(x′|x,a)<∞表示在状态x采取行动a∈Ax后，系统转移到状态x′(x′≠x,x,x′∈X)的即刻成本。在本研究中，c(x′|x,a)指的是项目加权拖期成本。令ψ(x′|x,a)表示在状态x采取行动a∈Ax，且系统转移至状态x′后新增的完工项目集合。因此，该决策过程对应的项目拖期成本为

(2)

2.2 最优策略

值迭代(Value Iteration, VI)和策略迭代是两种求解MDPs的基本算法，其中VI算法应用更为广泛。本文采用VI算法来求解模具项目调度的最优策略。令v(x)表示状态x∈X的函数值，则VI算法的核心就是迭代求解如下Bellman方程：

(3)

式中m表示第m次迭代。

当对于所有状态均有式的左侧等于右侧，意味着VI算法收敛，得到最优目标函数值v*(x0)。与此同时，可以利用下式获得各个状态下的最优行动：

(4)

3 近似策略

由于VI算法需要枚举所有可能的状态和行动，使得其在求解大规模问题时极易面临维数灾问题。相比于CPU耗时，内存消耗往往更容易成为VI算法求解大规模问题的瓶颈[4,7-11,34]。为此，本章将分别基于经典优先规则和ADP构建多种近似方法，以提高问题可求解规模。

3.1 基于优先规则的策略

在任意状态下，可以使用优先规则对等待任务进行排序，得到相应的任务开工决策。因此，一种优先规则可视为随机RCMPSP的一种调度策略。学者们针对调度排序问题提出了大量优先规则(Priority Rules, PRs)，其中部分优先规则也被应用于RCMPSP[20-23,25-26,34,38,42-44]。

本文所研究的模具项目调度决策目标是最小化总加权拖期成本期望，属于加权拖期优化问题。研究表明，改进交货期(Modified Due Date，MDD)[45]、加权改进交货期(Weighed MDD，WMDD)[46]、延期成本(Cost OVER Time，COVERT)[47]以及显著拖期成本(Apparent Tardiness Cost，ATC)[48]这4种优先规则在解决加权拖期优化问题时表现较好。为此，选择这4种优先规则作为模具项目调度近似策略，规则信息如表1所示。尽管这些规则策略可以单独使用，但是文献[34]表明，多规则组合(Multiple Rules Combination，MRC)能得到更优的结果。本文将在计算实验部分对基于单个优先规则和基于MRC的近似策略进行详细对比。

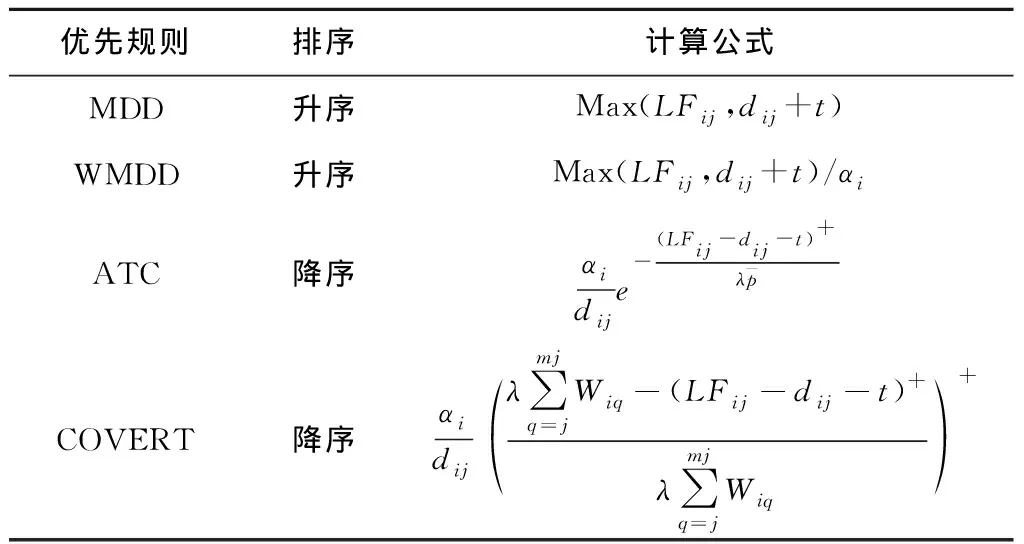
表1 所选4种经典优先规则

需要强调的是，本文在每一个决策时刻都是仅对当前等待任务进行排序，并采用尽可能早开工的原则选取开工任务。

3.2 基于GA的策略

如文献综述部分所述，除优先规则之外，被广泛应用于确定性RCMPSP的GA等智能算法也可视为随机RCMPSP的一种策略。文献[28]面向确定性RCMPSP，构建了一种能够定义任务优先级、任务延迟时间、项目投放时间的GA。本文将在该算法基础上构建基于GA的模具项目调度策略。由于本文项目到达时间已知，且任务遵从尽可能早开工的原则，将染色体简化为仅包含任务优先级。在模具项目调度之前，利用GA获得各任务优先级，该过程中需要采用仿真方法评估每个染色体的适应度函数值。在模具项目调度过程中的任意决策时刻，都将按照最优染色体定义的任务优先级选择开工任务。

本文GA种群的演化策略与文献[28]相一致，都包含精英个体保留、均匀交叉以及随机个体变异3种操作。关于基因表达和演化策略的详细描述见文献[28]，本文不作赘述。

3.3 基于Rollout与Post-Rollout的策略

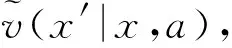
(5)

上述过程是ADP的基本思路[35]。ADP有效权衡了优化效果和求解效率，因此被广泛应用于包括随机RCPSP[6]和随机RCMPSP[36,37]在内的大规模MDPs问题中。

式(5)所示ADP是在系统经过一次状态转移之后估计值函数，因而称为单步Rollout算法[49-50]。单步Rollout算法通常采用启发式规则仿真来估计状态函数值，且所得结果优于所用启发式规则[51]。然而，Goodson等[52-53]指出单步Rollout算法在求解大规模问题时需要耗费大量时间进行仿真，并提出一种更加高效的Post-Rollout(简称PRollout)算法。如式(6)所示，该算法直接从决策后的状态xa开始仿真，极大地降低了仿真计算量。

(6)

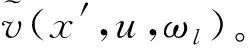
(7)

(8)

3.4 基于改进Post-Rollout的策略

尽管PRollout求解能力较Rollout有所提升，但其局限在于依然需要枚举每个状态的所有可选行动。对于大规模模具项目调度问题，一些状态下的任务开工组合规模将非常大，完全枚举所有可选行动将十分低效。针对该问题，本节提出一种改进的PRollout(improved PRollout)方法，其基本思路是先结合优先规则限定每个状态的可选行动空间规模，然后采用PRollout求解次优行动。

假定状态x∈X的等待任务集合为w，所用仿真规则集合为ζ，IPRollout算法的行动空间限制过程如下：

算法1可选行动空间限制过程。

2.for each u∈ζ，do

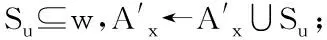
4.gj=gj+1/,∀j∈Su；gj=gj+1/(*kju),∀j∈wuSu；

5.end for

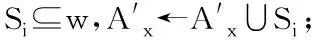
9.end for

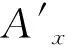
4 计算实验

为验证本文所构建的调度模型及方法的有效性，本章将基于随机生成的模具项目算例进行多组计算实验。计算程序采用C++编程实现，实验结果由该程序在配置为Intel Core CPU 2.9 GHz，128 G RAM的工作站上运行所得。

4.1 实验设计

本实验主要是测试和对比不同调度方法的求解能力和求解效率。为此，设置了小、中、大3种规模的算例，并设计了如下3组实验：

(1)第一组实验面向小规模算例，用于对比VI精确方法、表1所示4种规则、MRC方法、GA方法以及PRollout方法。由于本组算例的规模较小，将统一采用第2章所述MDPs模型进行计算，各方法的区别在于每个状态下获得的可选行动空间不同。

(2)第二组实验面向中等规模算例，用于对比IPRollout以及第一组实验中除VI之外的方法。由于状态数量太多，无法完全枚举，在求解每一个算例之前先随机生成一定数量的项目情景(工期样本)，然后令每种调度方法在每一种情景下进行决策，并取结果均值。其中，MRC与PRollout计算过程类似，是在利用几种规则获得当前状态的可选行动后，再根据优先规则仿真结果从中选择最优行动。

(3)第三组实验面向大规模算例，用于对比第二组实验中除PRollout之外的方法。本组实验过程与第二组实验过程相同。

实验考虑三种项目交货期环境(紧急、一般、宽松)，并假定任务工期服从泊松分布。利用项目总加权拖期成本期望、状态数、计算耗时指标，对比上述调度方法。

4.2 实验数据

本实验选用如图1所示模具项目网络。所有项目均具有该网络结构，但不同项目对应的项目金额、交货期及拖期惩罚系数不同。

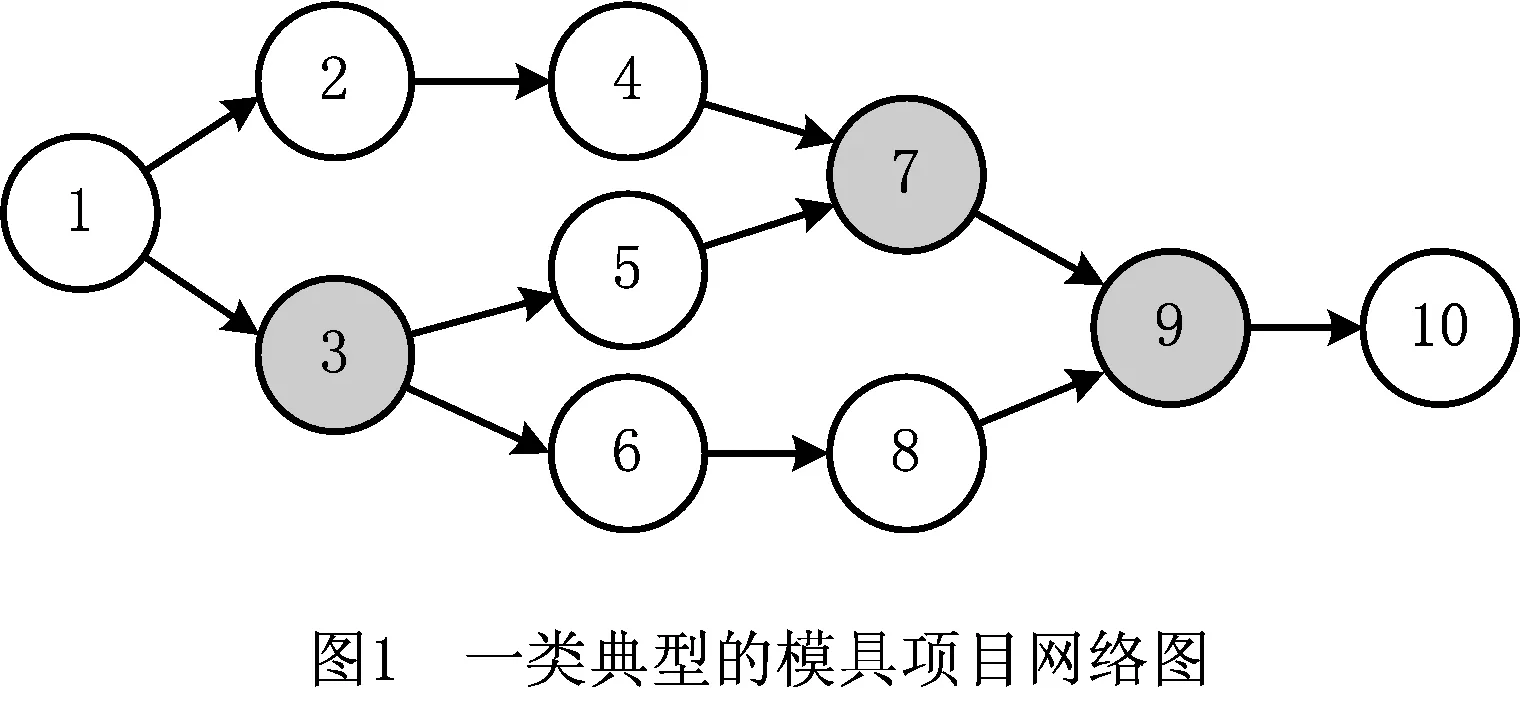
图1所示项目网络中各任务节点的工期均值E(d)={5,3,5,4,4,3,6,4,10,3}，项目关键路径长度均值Lcp=33d。其中，任务3、7以及9的工期不确定。这些任务可能的工期值按照对应泊松分布概率从高到低选取，当累积概率达到0.8时终止，最后将取值概率进行一致化处理。

在模具企业中，一类资源通常指一个工作中心或一个工作小组，任务节点与资源之间往往是一一对应关系。此外，每个任务在执行过程中通常只需要1个单位的资源(如1台设备或1名设计员等)。因此，设定资源种类数等于图1所示项目网络任务数，第j个任务节点对第k类资源的需求量rjk=1(当j=k)或者rjk=0(当j≠k)。此外，为了尽可能保持各类资源的负荷均衡性，令每类资源的数量与并行项目数及其对应任务的工期均值成正比。不失一般性，设定第k类资源的数量Mk=Hdj/15，其中H表示项目数量。

在生成项目算例时，每种规模的算例分别考虑3种不同的并行项目数量。其中：小规模算例项目数n={3,4,5}、中等规模算例项目数n={6,8,12}、大规模算例项目数n={25,35,55}。与此同时，设定项目交货期紧急系数ρ={0.8,1.0,1.2}。对于每一种规模的算例，在保持项目网络信息和资源信息不变的情况下，面向不同交货期环境分别独立随机生成10组项目信息，其中每个项目的具体信息按照表2所示概率分布随机生成。

表2 项目基本信息参数设置

此外，本实验采用与文献[28]计算实验相同的GA参数设置方法，如表3所示。

表3 GA参数设置

4.3 近似方法参数灵敏度分析

由于PRollout和IPRollout基于仿真决策，其优化效果受仿真次数影响。此外，IPRollout的优化效果还受可选行动数量影响。因此，本节将通过灵敏度分析来合理设置这两个参数。

首先，利用PRollout方法求解中小规模算例，以获得合理的仿真次数设置。接着，利用IPRollout方法求解大规模算例，以获得合理的可选行动数量。考虑到仿真过程的随机性，本文采用不同的随机种子对每组算例进行10次求解，取均值作为最终结果。为了更好地展示计算结果，令每组实验中的结果除以最大值，所得比值称为一致化加权拖期总成本(Unified Tardiness Cost，UTC)，结果如图2所示。

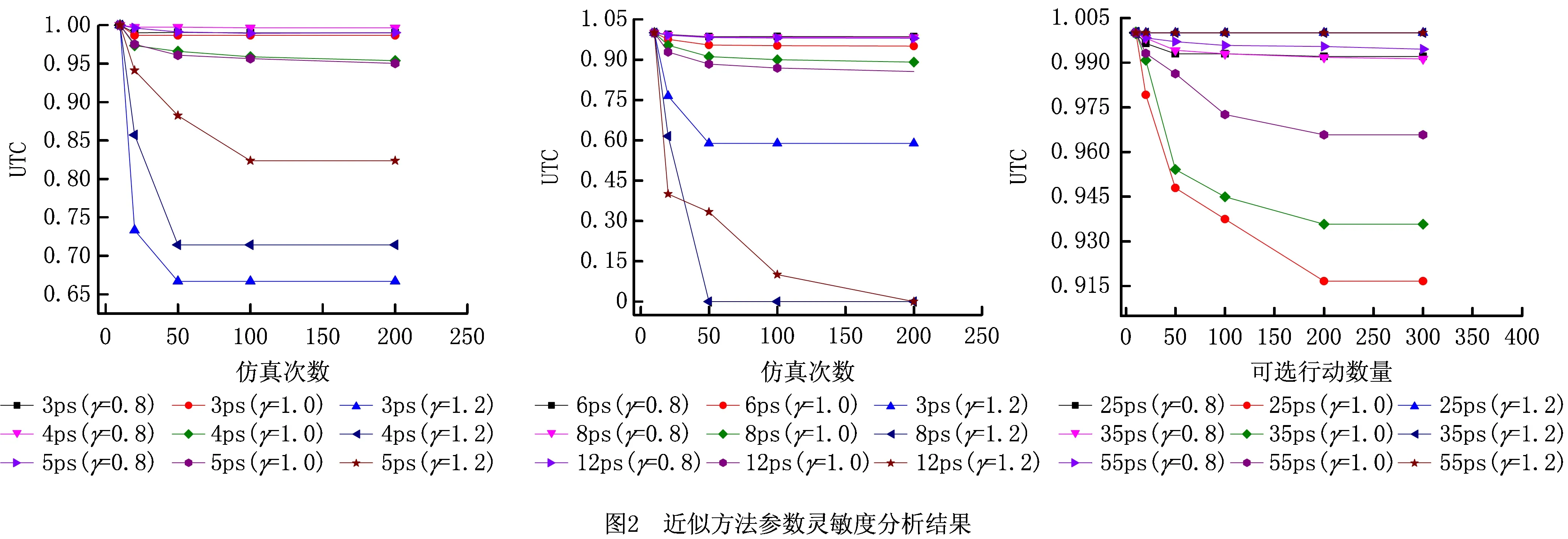
由图2可以看出，随着仿真次数和可选行动数的增加，近似方法的优化效果显著提高。然而，当这两个参数增长到一定程度时，优化效果趋于稳定。为获得更高的计算效率，本实验设定仿真次数为100，可选行动数为200。

4.4 结果分析

在上述实验参数设置下，分别完成了3组计算实验，并得到不同方法对应的平均加权总拖期成本。为了更清晰地展示不同方法之间的差别，构建了如式(9)所示的平均加权总拖期成本差异百分比指标：

(9)

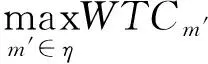
表4 基于Dev(WTC)%指标的调度方法对比

由表4所示结果，可以得到以下实验结论：

(1)在经典优先规则表现方面，各规则在不同项目环境下的表现有所差异，WMDD和COVERT在交货期紧急和一般环境下的表现明显优于其他规则，而MDD在宽松交货期环境下的表现则更好。虽然其他学者认为ATC在交货期宽松的动态Jobshop环境下表现较优[48,54]，但是在本实验环境下该规则的表现并无优势。

(2)在近似方法优化效果方面，MRC和PRollout均优于单一规则，且在小规模算例环境下的表现接近VI精确算法。PRollout和IPRollout在中大规模算例环境下的表现最优，MRC次之。GA方法虽然也在大多数情形下表现优于优先规则，但是与MRC、PRollout、IPRollout之间还存在着明显的差距。

(3)在项目环境对调度方法的表现影响方面，各方法优化效果之间的差距随着交货期紧急系数的增大而增大。这是因为COVERT、WMDD以及ATC等加权类规则在选择任务开工时会侧重于权重大的项目，导致宽松环境下的决策过于保守。相比之下，PRollout和IPRollout等方法在仿真过程中能够较为准确地预测各项目的拖期，从而可以做出更加合理的决策。

在实验过程中收集的各方法计算耗时对比结果如表5所示，小规模算例下的状态空间规模对比结果如表6所示。由于基于PRs和GA的策略在求解小规模算例时都对应离散时间马尔可夫链，对应的状态空间规模相近，因此表6将两者结果放在一起取均值。

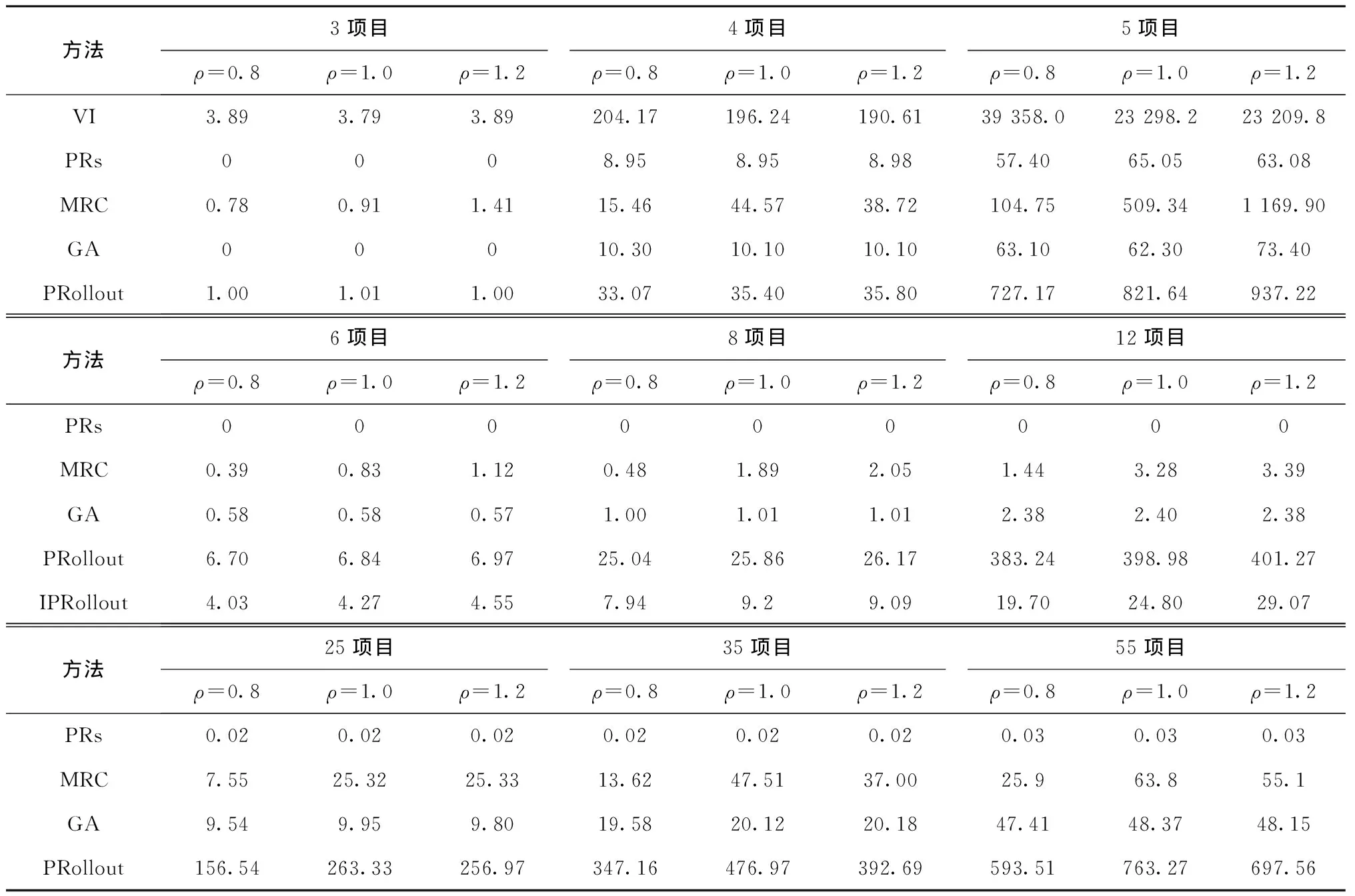
表5 各调度方法计算耗时对比 s

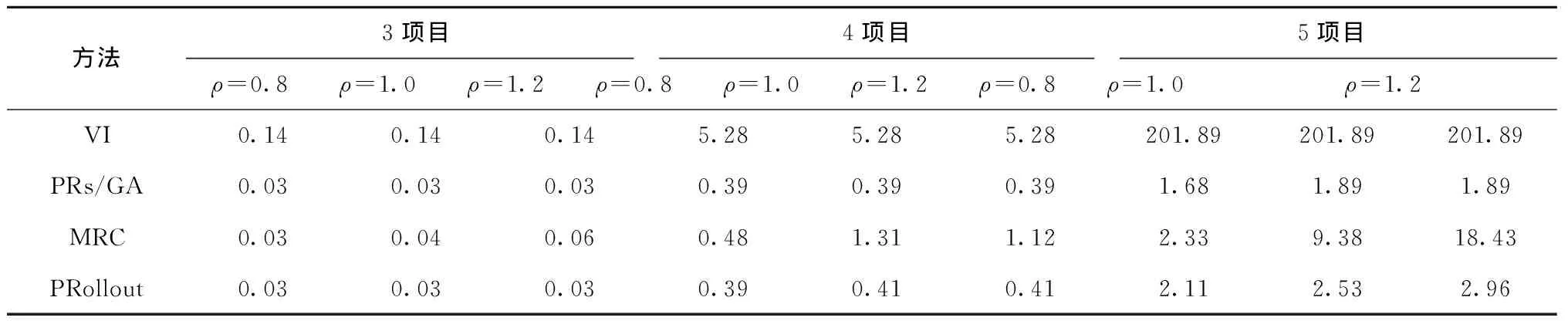
表6 小规模算例下各调度方法状态空间规模对比 ×106

从表5和表6计算效率指标可以看出，VI精确方法所需计算耗时和状态空间随着项目数增加而急剧增长。求解5个项目的算例大约需要消耗70 G内存，且耗时超过10 h，已经达到精确求解极限。相比之下，其他几种近似方法所需计算耗时和状态空间规模要小得多，尤其是本文提出的IPRollout方法求解55个项目的算例仅需10 min左右，且优化效果明显好于经典优先规则、GA及MRC方法。换言之，IPRollout方法能够更好地权衡决策优化效果和决策效率，可用于解决工程实际问题。

5 结束语

本文研究了多项目共享有限资源且部分任务工期离散随机下的模具项目调度问题，基于离散时间MDPs理论构建了以总加权拖期成本期望最小为决策目标的随机模型。针对VI精确算法求解大规模问题面临的状态和行动空间维数灾，分别提出了基于经典优先规则(MDD,WMDD,ATC和COVERT)、GA和ADP(现有PRollout和新提出的IPRollout)的近似方法。最后，基于随机生成的模具项目算例设计了多组计算实验，对比了不同项目规模、交货期紧急程度下各调度方法的优化效果和计算效率，验证了所构建模型和方法的有效性。实验结果表明，VI精确算法仅能够求解5个以内的项目问题，而优先规则虽然有效规避了维数灾，但是在复杂问题环境下的优化效果较差。相比之下，本文提出的IPRollout方法能更好地权衡优化效果和计算效率，可用于求解大规模工程实际问题。在下一阶段工作中，将研究构建更高效准确的值函数近似方法，以进一步提高IPRollout方法的优化效果及求解效率。