基于因果行为轮廓的流程变体聚类挖掘方法

方 欢，金朋朋，方贤文，王丽丽

(安徽理工大学 数学与大数据学院，安徽 淮南 232001)

0 引言

流程变体(process variants)可以被定义为系统流程族(模型)中相似但不同(similar-but-different)的模型(片段)，即这些模型(片段)至少有一个共同的特征，也至少有一个特征相互区分。从流程系统粗粒度的角度分析，流程变体是流程族模型中从基模型衍生出的其他相似流程模型;从流程系统细粒度的角度分析，流程变体是指各流程模型中具有某些共性且又具备各自个性的模型片段。流程变体的研究在过程感知系统[1-2]、自动化制造系统[3]中有着广泛的应用。

业务流程系统的变化挖掘融合了过程挖掘和适应性流程管理两方面研究内容[4-11]，通过日志的过程挖掘技术来发现或收集流程管理系统所实施的变化操作，近年来也取得了一系列研究成果，如文献[4]研究了在已知流程变体的情况下，挖掘与流程变体适合度最高的过程模型，文献[5]提出一个研究设计来测试嵌套深度对实验中变化模式使用的认知复杂性的影响，文献[6]提出一种在自适应流程管理系统中挖掘变化日志的方法。通过流程挖掘所发现的变化流程提供了所有变化的总的概述，反过来又可以作为各种流程行为改进的基础。文献[7]提出一种从事件日志集合中提取可变的过程片段的方法，并提出一个新的过程片段定义，称为形态学片段，用以支持方法的组合性和灵活性。然后，提出直接从过程事件日志中提取形态片段的算法，并提出支持用于检测和分类形态片段以便重用的算法。文献[8]从行为轮廓的角度出发，通过比对系统实际日志和参考模型，来定位和挖掘系统模型可能发生的结构变化，并总结了几种经典的变化结构模式。文献[9-11]均从事件日志出发，通过定义变元片段，提出相应的日志挖掘方法来发现日志中的变元片段。

综上可知，已有针对变体挖掘的研究大都基于参考模型已知的情形，然而在实际应用中存在这样一种应用场景：存在多个类似的流程系统(每个系统两两不完全相同)，考虑使用一个通用模型来对这些功能相似的系统进行业务融合。因此，开发一种更加简洁概括地描述这些流程变体的方法是十分必要的。与文献[6]的出发点刚好相反，本文结合行为轮廓相关知识，通过分析活动间的行为关系，将若干个流程变体合并到一个通用参考流程模型中，使所得到的通用模型能“最好”地适配这些已有的流程变体。

本文主要创新之处在于：以往的变体挖掘算法着重于研究变体与原模型之间的联系与差异来对变体进行配置，而本文的研究工作可以摆脱原模型的约束，在无原模型的情况下，应用矩阵和余弦相似度的相关知识分析确定流程变体活动对的行为关系，并进一步进行反复迭代，将所知变体活动聚类合并成一个新的模型。

1 基本概念

定义1[12]流程变更和流程变体。P表示所有合理流程模型的集合，C表示可能的过程变化集，包含插入、删除和移动活动等变化。

两个流程模型S,S′∈P，令Δ∈C是根据高级变化操作表示的过程变化，且令σ=(Δ1,Δ2,…,Δn)∈C*是在初始模型S上执行的流程变化序列。则有：

(1)S[Δ>S′当且仅当Δ适用于S，S′是由于应用Δ到S而产生的流程模型。

(2)S[Δ>S′当且仅当∃S1,S2,…,Sn+1∈P,且S=S1,S′=Sn+1，得出Si[Δi>Si+1(i∈{1,2,…,n})，将S′表示为S的流程变体。

定义2[12]偏差和距离。两个流程模型S,S′∈P之间的距离d(S,S′)是指将S转换为S′所需的最小数量的高级变换操作，即d(S,S′)=min{|σ||σ∈C*∧S[σ>S′}。相应的变化操作序列σ表示为S和S′之间的偏差B(S,S′)，即B(S,S′)=|σ|。

S和S′之间的距离描述的是将S转换为S′所需的最小数量的高级变换操作。高级更改操作的简单示例包括在工作流网中实现的插入活动、删除活动和移动活动[13]。插入和删除修改流程模型中的活动集时，移动更改活动位置，从而移动流程模型中的订单关系。例如，操作move(S,A,B,C)将活动A从其在流程模型S内的当前位置移动到活动B之后和活动C之前的位置；操作delete(S,A)是删除流程模型S中的活动A；操作insert(S,X,A,B)是在流程模型S中将新活动X插入到活动A之后和活动B之前的位置。文献[13]中描述了关于正确使用这些操作以及正式的前后条件的问题。尽管所描述的变更操作是在工作流网中进行讨论的，但它们是通用的，可以很容易地与其他传统的流程模型一起应用。文献[14]进一步将这种变换操作引申到日志挖掘中，实现日志驱动下的系统行为变化挖掘。相应的变化操作序列表示为S和S′之间的偏差B(S,S′)。通常，这种距离可以测量模型变换的复杂度。

定义3[15]行为轮廓。令S=(N,M0)是一个网系统，其中N=(P,T,F)，初始标识为M0且T′⊆T是一个变迁集xy。若变迁对(x,y)∈(T′×T′)满足下面之一条件：

(1)若x≻y且yx，则称严格序关系，记作x→y。

(2)若xy且y≻x，则称严格逆序关系，记作x→-1y。

(3)若xy且yx，则称排他关系，记作x+y。

(4)若x≻y且y≻x，则称交叉序关系，记作x//y。

以上几种关系构成网N在T′上的行为轮廓，记作BPT′={→,←-1,+,//}。

定义4[15]因果行为轮廓。令S=(N,M0)是一个网系统，其中N=(P,T,F)，初始标识为M0且T′⊆T是一个变迁集，BP={→,←-1,//,×}是在T′上的行为轮廓。

(1)若所有发生序列σ，满足(N,M0)[σ>(N,M′)且x∈σ⟹y∈σ，则称(x,y)是共现关系，记作x>>y。

(2)CBT′={→,←-1,+,//,>>}是网N在T′上的因果行为轮廓。

2 动机案例

以图1为例，参考模型S已配置为5个流程变体Si∈P(i=1,2,…,5)，变体模型Si对应权重ωi(i=1,2,…,5)是根据实际案例研究，计算执行变体模型的流程实例数量与总流程实例的比值得到的。如在图1中，所有流程实例的30%都是根据变体S1执行的，而15%的实例是执行的变体S2，以此类推。因此，ωi(i=1,2,…,5)=30%，15%，20%,20%,15%。

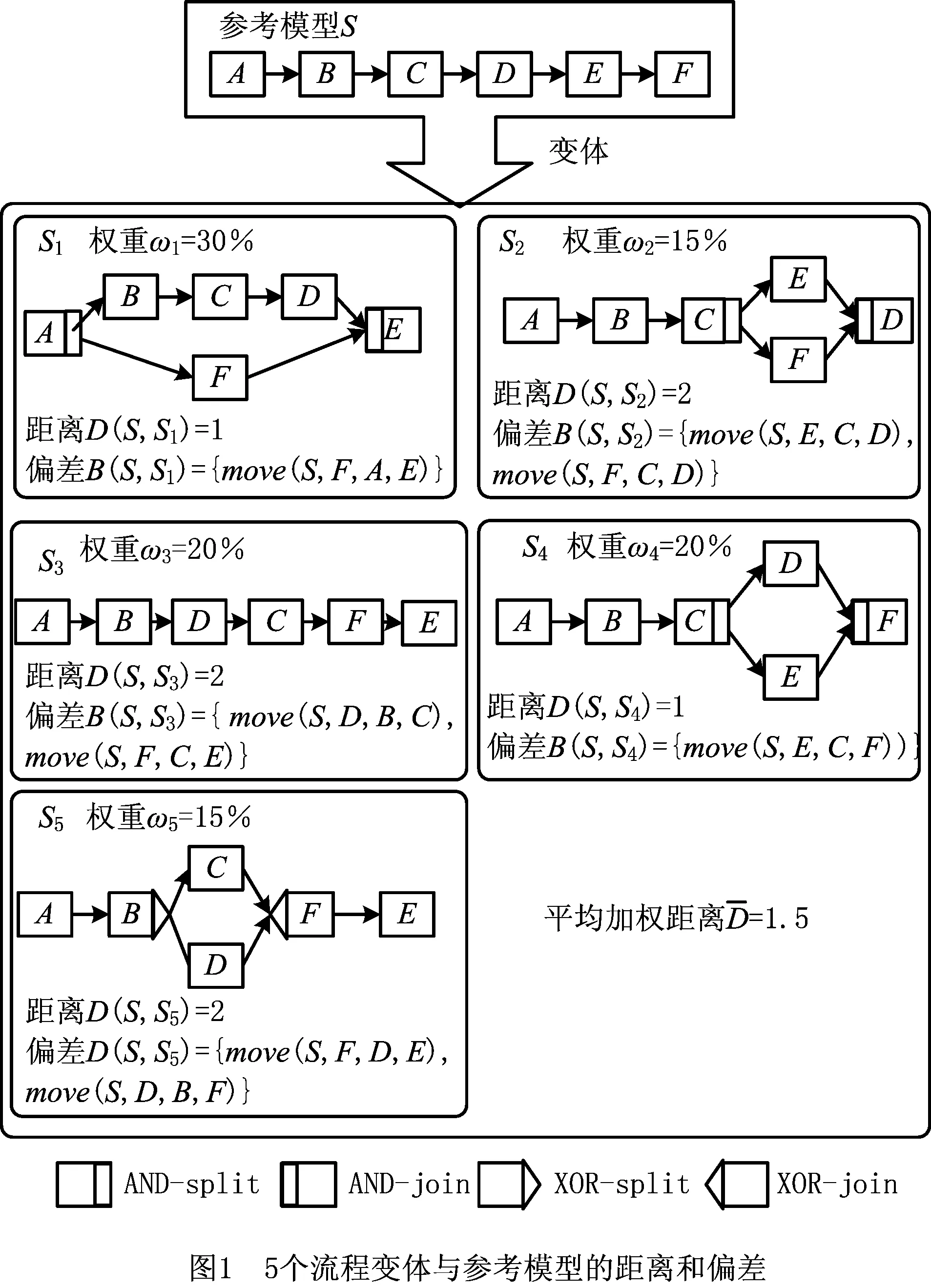
一般情况下，可以用参考模型和流程变体之间的平均加权距离来表示它们之间的相似程度。而改进挖掘算法的目标就是发现一组流程变体或者称为变体集的参考模型，并使得这个新模型与这些变体的平均加权距离最小。下文假设每个流程变量具有相同的活动集。

文献[16]中提出一种基于后继关系的行为块挖掘算法，这种块结构的挖掘方法相比直接挖掘，更加精确高效，因此本文也考虑采取块结构化的流程挖掘方法，可以通过扩大块结构来构建新的参考模型。首先识别可以形成块的一个活动对，然后将该块与其他活动分别合并以形成更大的块，直到所有活动都被合并为一个块结构，最后得到新的模型。

3 变体挖掘方法

正如上文提到的，改进变体挖掘算法的目标就是发现与变体的平均加权距离更小的新的参考模型。为方便研究与计算，应用矩阵的知识，可以将变体模型转化为对应矩阵，即将变体与参考模型的活动对之间的行为关系用矩阵形式表达，然后对这些矩阵进行聚合，得到一个可以反映变体集的矩阵，进而基于该矩阵对活动进行聚类，从而一步步构建活动块，直到最后将所有活动都包含在内，形成新的流程模型。该方法简述如下：

(1)对于所有变体，建立相应的矩阵模型，并将其聚合成一个可以代表变体集的多维矩阵。

(2)根据得到的矩阵，确定要在块中聚类的活动。

(3)确定已聚类活动在此块中应具有的行为轮廓关系。

(4)在步骤(2)和步骤(3)中构建新块后，通过相应地调整多维矩阵来反映活动的聚类。

(5)重复步骤(2)～步骤(4)，一直迭代到所有活动聚集在一起，构造出新的参考流程模型。

3.1 聚合矩阵

通过观测得出，当删除一个活动时，既不会影响该活动的后继，也不会影响其前驱，因此不会影响其他序关系。为了在方法中加入该特性，不仅只考虑两个活动之间的直接前驱和后继关系，还需考虑所有活动对之间的控制依赖关系。这就很容易想到用定义3中行为轮廓的概念来描述该偏序关系。进一步从逻辑上说，根据定义4的因果行为轮廓，可以通过考虑相应变体与参考模型之间的5种行为关系来构建对应矩阵。

定义5对应矩阵。设流程模型S=(N,E,…)∈P且N={a1,a2,…,an}，矩阵A|N|×|N|称为S的对应矩阵，Aij表示活动ai,aj∈N之间的行为轮廓关系，其中i≠j，则有：

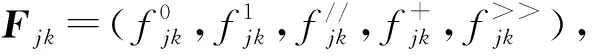
根据上述定义，可以将5个流程变体的对应矩阵融合成包含因果行为轮廓关系的聚合矩阵，且很容易理解，在聚合矩阵中，研究一个活动与其自身的行为关系并没有意义，因此它的主对角线总是空的，对于所有其他元素，可能某个维度值为0，由于这样的情况很多，在图中不进行填补，具体情况如图2所示。

接下来的问题是如何对聚合矩阵进行进一步的分析处理，在研究行为轮廓一致性时得到一定的启发，如果一个活动与其他活动具有相同的行为关系，则可以将它们聚集成一个小块。同样的，这种思路也可以用于变体模型。当然在一般情况下，往往不可能有两个活动在所有的变体中行为关系都一致，因此需要在此基础上进行进一步考虑。

3.2 活动聚类

如何确定变体集中聚类的活动成为首要解决的问题，其关键在于活动对的确立依据将影响最后聚类所得模型的优劣。在已有文献中，欧几里得距离经常被用来描述个体差异之间的距离，欧氏距离主要有两个弊端：①欧氏距离的值域太过宽泛，不利于描述活动对之间联系的紧密程度；②欧氏距离描述的是绝对空间距离，只能体现个体数值特征的绝对差异，无法体现行为关系。定义4中提出余弦相似度是通过测量两个向量的夹角的余弦值来度量它们之间的相似性，这个概念很好地排除了欧氏距离弊端，因为它对绝对数值并不敏感，取值范围为[0,1]正好切合相似度0～100%，且已经广泛应用于各种聚类的算法中，因此同样可以用余弦相似度对活动间的行为关系进行聚类分析。在文献[17]中，两个n维向量X，Y的余弦相似度被定义为：

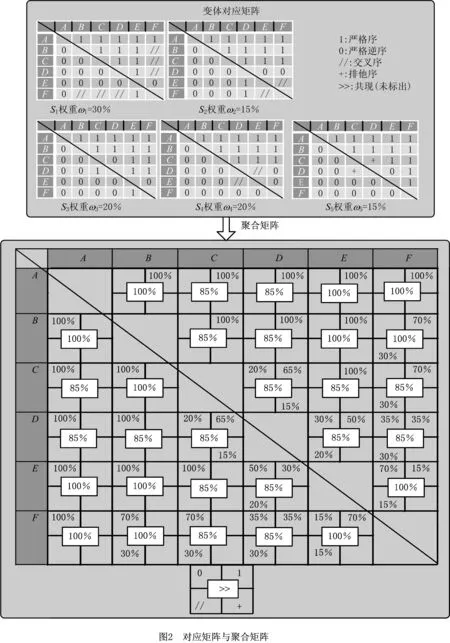
cosine(x,y)∈[0,1]。

单纯考虑余弦相似度一个维度时，只能体现两个向量相似程度，无法体现行为关系的联系强弱，因此有必要对其进行加权。在因果行为轮廓关系包含的5种行为关系中，存在严格性上的差异。比如：交叉序关系在潜在的发生序列中可以被看作无任何限制；而严格序和严格逆序关系定义了两个变迁的特有发生序列；另外排他序关系禁止了两个变迁在一个序列中同时发生。因此，可以认为交叉序关系是最弱的关系，其次是严格序和严格逆序关系，排他序关系最强。由于共现关系与其他关系存在重叠，这里不予考虑。因为没有查到关于这种赋权问题的相关文献，所以根据案例研究的经验，决定使用权值来表示行为关系的严格性强弱，具体情况如表1所示。

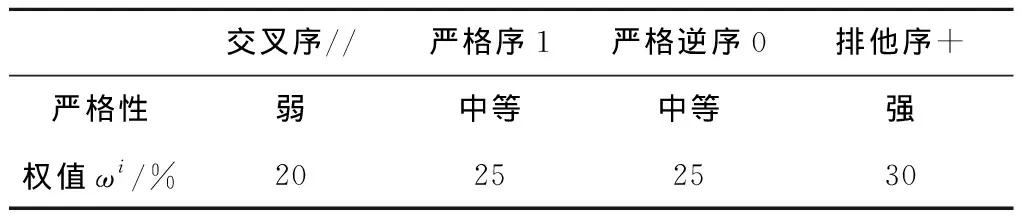
表1 对4种行为轮廓关系赋权

4种行为轮廓关系的权值可以表示为ω″=20%，ω1=25%，ω+=30%，ω0=25%，则可以对原本的余弦相似度进行加权，为适应聚类需要定义新的加权余弦相似度。

定义7加权余弦相似度。两个五维向量X，Y，α∈{0,1,//,+}，ωα=25%,25%,20%,30%,则它们的加权余弦相似度

COS(X,Y)∈[0,1]。

如果COS(X,Y)=1，则X和Y在它们的方向上完全匹配；相反的，COS(X,Y)=0意味着它们根本不匹配。这个值越接近1，匹配度越高。例如，当比较FAF和FBF之间的相似程度时，计算COS(FAF,FBF)=93.4%，说明它们的相似度较高。

基于加权余弦相似度，进一步引入分离的概念。分离SEP(A,B)表示与其他活动相比，活动A和B的顺序关系相似程度。仍然在图1的示例中，SEP(A,B)由COS(FAC,FBC)，COS(FAD,FBD)，COS(FAE,FBE)和COS(FAF,FBF)的接近程度决定。通常可以将集群分离度定义为：

×100%，SEP(A,B)∈[0,1]。

式中N为对应活动集，通过将∑x∈N{A,B}COS(FAx,FBx)该表达式除以|N|-2(其中2表示当前拟研究的两个活动A,B)，将其值规范化为介于[0,1]之间的范围，最后结果以百分数形式表示出来。对于图2中的聚合矩阵，计算SEP(A,B)=98.4%。通过测量每对活动与其他活动之间的分离程度来确定最适合形成一个块的活动对。这个值越高，两个活动就越适合集群化。对于图2中的示例，所有分离度如表2所示，将该表命名为分离度表。由于SEP(X,Y)=SEP(Y,X)，拟研究的活动对之间并无顺序关系，表2中不再重复列出。

表2 聚合矩阵的分离度表

从表中可以直接看出活动A与B的分离度最高，因此创建活动对(A,B)作为第一个块结构。

3.3 确定块内顺序

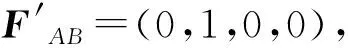
下面形式化定义一个余弦偏差值来评估所选定偏序关系偏差程度：

按照公式，计算δAB=0，表明活动A和B选择严格序关系很准确，并无偏差。

3.4 调整聚合矩阵

通过应用加权余弦相似度找到了参考过程模型的第一个模块(A,B)，并进一步确定了满足A→B，余弦偏差值为0，更表明了这个关系的准确性，接下来需要研究这个新的模块和其他活动之间的关系，从而对原本的聚合矩阵进行调整。

对于图1中的流程变体，A和B并不一定能够单独构成基本块。比如A和B就不能构成S1中的基本块。然而通过分析，A和B最适合来形成第一个块结构。因此，需要通过计算A、B和其余活动之间的偏序关系，对原来的聚合矩阵进行调整。主要制定两条调整规则：①原本聚合矩阵中的其他活动之间的关系不需要改变；②将(A,B)看作一个活动对来计算与其他活动的关系。规则形式化表示如下：

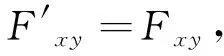
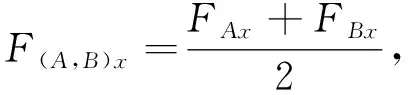
由于A和B被包含它们的块替换，即将该块视为单个活动，重新计算后得到的矩阵比原本的小一个维度。基于以上规则，对原本的矩阵进行处理就可以构建包含活动对(A,B)的新的聚合矩阵，如表3所示。

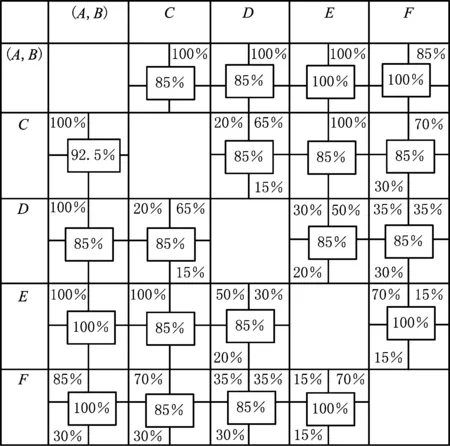
表3 包含(A,B)的新聚合矩阵

3.5 结果分析

在第一次迭代中，(A,B)被聚类成一个块；在下一个迭代中，重复3.2节～3.4节，活动C与(A,B)聚类成一个新模块。以此类推，最后在第5次迭代之后，所有活动都聚集在一个块中，得到新的参考模型。重复的迭代过程不再赘述，图3直接展示了案例重新发现原始模型的整个迭代过程，还特别标注了每一步的余弦偏差值，反映了不同迭代阶段所选择弱序关系的准确性。

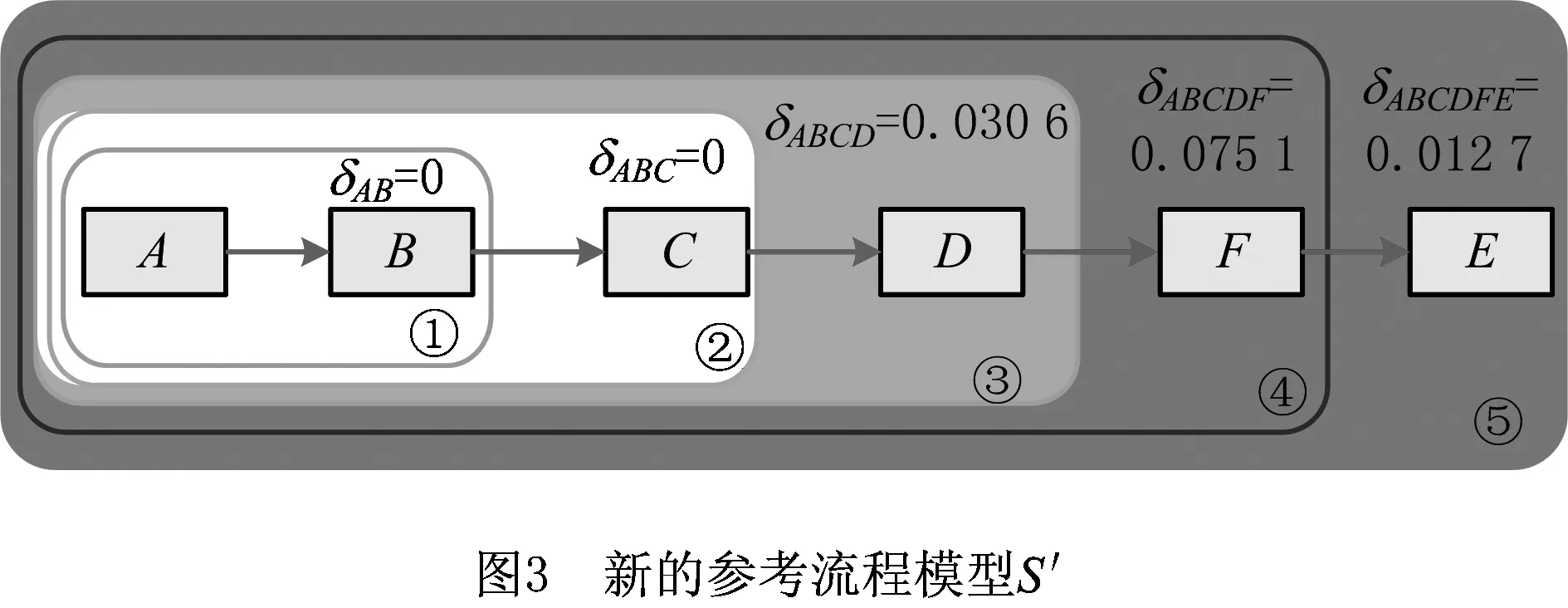
很容易理解该挖掘算法的复杂性为Ο(n3)。与大多数聚类数据挖掘算法一样，该算法试图在多项式时间内解决一个复杂组合优化问题。这虽然有利于解决大规模的问题，但缺点也很明显，只是考虑了局部并未站在全局角度。在结果上看，本文用聚类算法找到了一个新模型，且从变体集和参考模型的距离上看，原参考模型S的平均加权距离为1.5，而新的流程模型S′经过计算只有1.15，确实达到了预期目的。

3.6 算法描述

通过3.1～3.3节描述可知，本文方法首先由所有变体建立相应矩阵并融合成聚合矩阵，然后利用加权余弦相似度聚类活动块，接着分析块内行为轮廓关系，调整聚合矩阵来反映新模块与其他活动的行为关系，最后重复上述操作直到所有活动都聚集在块内，构造出新的参考流程模型。下面给出具体的聚类算法，称为基于因果行为轮廓的流程变体聚类挖掘(Causal Behavioral Profiles based Process Variants Cluster Mining, CBP-PVCM)算法。

算法1CBP-PVCM算法。

输入：流程变体集Si(i=1,2,…,n)及对应权重ωi(i=1,2,…,n)。

输出：新的参考模型S′。

步骤3计算所有活动间加权余弦相似度COS(X,Y)，基于此再计算活动间的分离度SEP(X,Y)，选择分离值最大的活动对作为一个活动块。

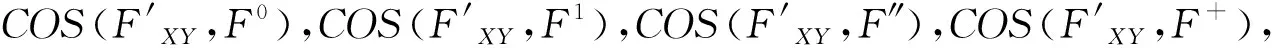
步骤5根据两条调整规则，将活动块作为一个活动重新调整融合矩阵S|N|×|N|。

步骤6循环运行步骤2～步骤4共计(|N|-1)次，得到新的参考模型S′。

4 仿真实验

假设所有流程变体的行为都可以被执行日志完全表示，即枚举图1中每个流程变体可产生的所有可能的迹，由这些迹组成的完备日志如表4所示。根据过程挖掘的相关知识，通过挖掘完备日志就可以发现新模型。

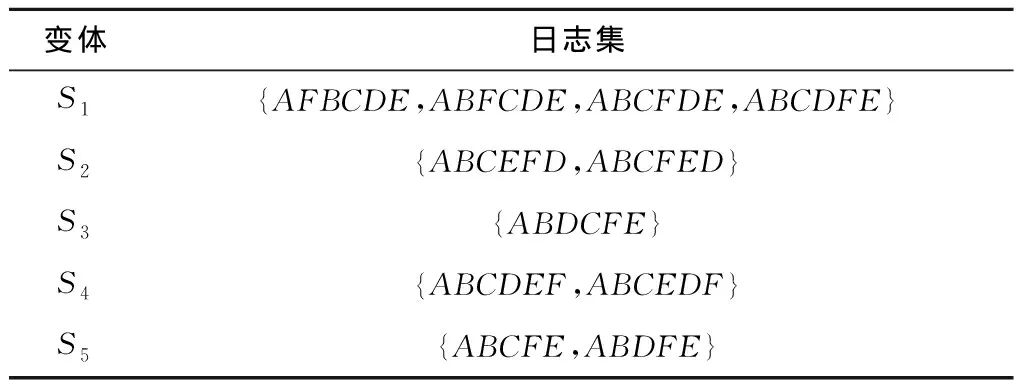
表4 变体对应执行日志

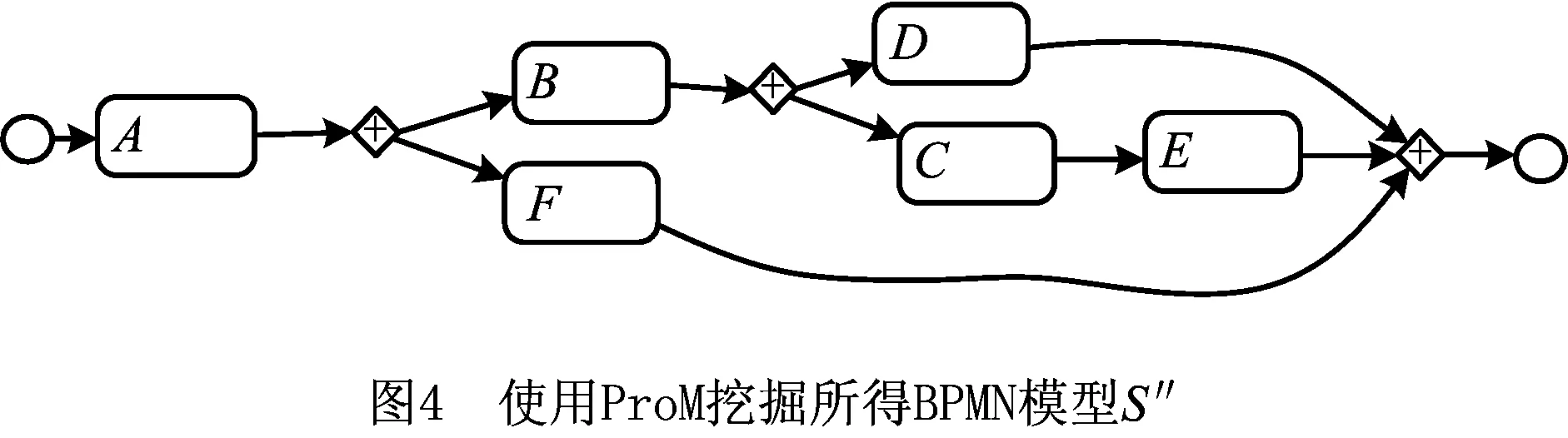
为了说明算法CBP-PVCM的有效性，在例子中，本文根据变体模型生成日志文件，再选择传统的基于完备日志的过程挖掘算法来发现新模型，然后就可以计算其与变体集之间的平均加权距离，最后将结果进行对比。为方便快捷，可以使用ProM框架对生成日志进行挖掘，分别使用Alpha算法，Alpha+算法，Alpha++算法[18]以及ILP算法[19]挖掘出了相同的BPMN模型，如图4所示。

有了该BPMN模型，就可以计算它和5个流程变体之间的距离，进而计算出平均加权距离。将S，S′和S″列为候选模型集，其对比结果如表5所示。由表5易知，本文使用的聚类算法所得模型S′与流程变体集平均加权距离为1.15，而使用ProM框架中的流程挖掘算法所得BPMN模型S″与变体集平均加权距离为1.85。

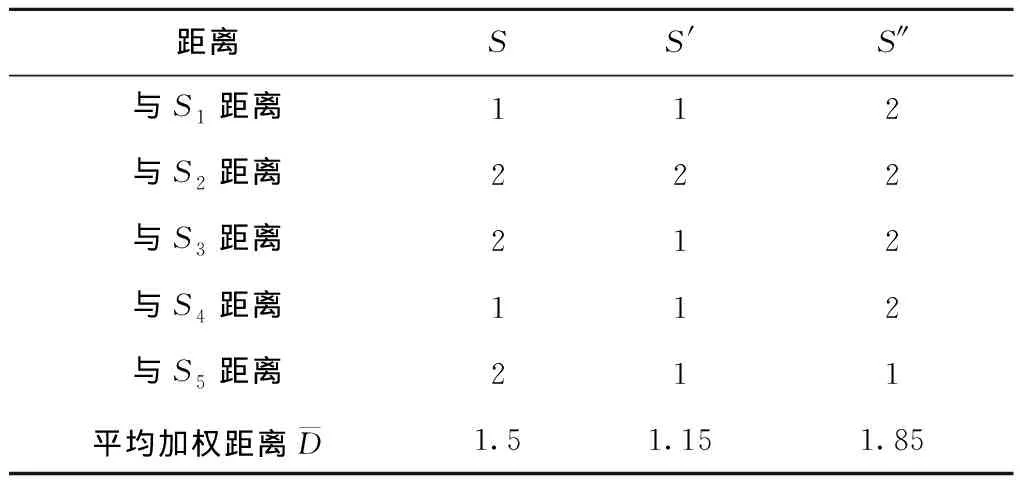
表5 候选模型集与变体之间的距离

根据该结果并不能认为过程变体挖掘一定优于流程挖掘，因为它们本身的目的就不相同。与通过学习系统行为来发现底层流程模型的流程挖掘相比，流程变体挖掘更侧重于发现一个可轻松配置不同流程变体的参考流程模型，但可以肯定的是，这种基于因果行为轮廓采用加权余弦相似度聚类的算法在发现参考模型方面是可行且有效的。

除此之外，将本文方法与常用的启发式算法[20]进行对比。启发式算法的基本原理是从一个原始模型出发，在设置的最大允许距离内搜寻新的模型，直至得到的新模型满足和变体集的平均加权距离比原始模型更小[20]。显然，该算法的主要缺点包括：①对用户敏感；②算法是NP-hard的；③并未考虑活动间的行为关系。而本文方法克服了这几个问题，表6给出了两种方法的各方面对比，更直观地展示了两种算法的差异。

表6 聚类算法与启发式算法定性比较

下面给出一个具体示例，为方便起见，依然以图1为例，对两种算法的结果进行对比，关于启发式算法的具体内容在文献[20]中有清晰描述，这里不再赘述。通过具体案例和算法复杂度，可以预估算法运行时间，并对结果进行比较。表7给出了具体的比较结果。

表7 聚类算法(本文方法)与启发式算法[20]示例结果对比

由比较结果可知，虽然在示例中启发式算法得到了与本文算法相同的模型，但是由于启发式算法需要多次计算新模型与变体之间的平均加权距离，并进行一一对比，反复的迭代过程大大增加了执行时间。随着变体数和活动数的扩大，启发式算法执行时间过长的弊端就会更加明显，而且用户如何设定合适的最大允许距离也会成为一个重要问题。相比而言，本文算法具有运行时间短，无需原始模型以及将活动间的行为关系考虑在内等优点。

通过将本文方法与传统的流程挖掘算法以及经典的启发式算法进行对比，表明了该方法在流程变体挖掘方面是行之有效的，且这种结合因果行为轮廓的聚类方法大大减少了执行时间，能够更加快速准确地发现新的流程模型。

5 结束语

本文提供了一个基于因果行为轮廓并结合余弦相似度的聚类挖掘方法来挖掘块结构的流程变体，以发现一个可以比原始的参考模型更容易配置这些变体的新参考流程模型。该算法具有多项式复杂度Ο(n3)，在解决实际问题时能够按照需要进行扩展。具体案例结果表明，使用该方法发现的参考模型比系统中已知的所有流程模型更好，对变体配置更为轻松。仿真实验结果还表明，挖掘到新的参考模型也比基于一些传统的过程挖掘算法发现的流程模型要好得多，比启发式算法更迅速准确地发现新的流程模型，因此本文算法在挖掘这种配置变体的参考流程模型时是可行且有效的。

在未来研究中，希望能够将该算法进行程序实现并应用于ProM软件中，此外在研究挖掘流程变体时，希望可以结合关联规则，对变体集中的活动挖掘不频繁行为模式，这样也许不仅能提高挖掘的效率，还能评估发现模型的准确性。