可变负载的准零刚度隔振器特性*

康冰冰， 李海军， 林学森， 王景霖， 邓 力

(1. 海军航空大学航空基础学院 烟台，264001)(2. 海军航空大学岸防兵学院 烟台，264001)(3. 故障诊断与健康管理技术航空科技重点实验室 上海，201601)

引 言

为了提高被动隔振器的低频隔振能力，降低起始隔振频率，需要降低隔振器的刚度，但这与隔振器的承载能力相矛盾。为此，准零刚度隔振器应运而生。准零刚度隔振器的基本原理是通过引入负刚度机构，抵消隔振器的正刚度，既保证隔振器的承载能力，又能使隔振器在静平衡位置的刚度接近0。准零刚度隔振器实现形式很多，Carrella等[1]分析了由线性斜置弹簧提供负刚度的准零刚度系统，研究了该系统的基本特征。Liu等[2]利用预压的欧拉梁产生负刚度，抵消线性弹簧的正刚度，达到准零刚度的特性。Zhou等[3]设计了带有凸轮滚子弹簧机构的准零刚度系统，该隔振器是一种分段非线性隔振系统。Robertson等[4]利用磁性弹簧实现准零刚度，该隔振器具有弱非线性、低固有阻尼的特点。Xu等[5]也提出了一种高静低动磁性隔振器。Zhou等[6]将3个紧凑的准零刚度弹簧组成1个金字塔式支柱，由4个支柱构成六自由度准零刚度隔振系统。Zhu等[7]采用磁悬浮技术实现了准零刚度。徐道临等[8-9]还设计了一种屈曲板型准零刚度隔振器和橡胶弹簧构成的准零刚度隔振器。

以上隔振器的参数一旦确定，不能改变，在过载或欠载情况下，高静低动的力学特性将发生改变。程春等[10]研究了超载、欠载情况下的准零刚度特性，结果表明，载荷变化会导致隔振效果变差，但是依旧优于线性系统。考虑到负载变化带来的问题，Lan等[11]研究了不同负载对准零刚度特性的影响和不同负载下隔振器的调整机制。徐道临等[12]提出一种气动可调式的隔振器，通过改变气缸内气体压力来适应载荷变化。考虑到隔振器的负载变化问题，笔者提出了一种机械式的可调隔振器，只需要改变准零刚度弹簧倾斜角度，便可适应负载的变化，调节简单，所需能量少。

1 准零刚度弹簧模型

准零刚度弹簧如图1所示，该弹簧的特点是结构紧凑，由套筒、活塞、杆、线性弹簧和负刚度机构等组成。线性弹簧的刚度为k，支撑负载载荷。负刚度机构如图2所示，由凸轮、欧拉梁和滚轮等组成。凸轮固定在活塞杆上，半径为r1；欧拉梁固定在套筒上，长度为S；滚轮固定在欧拉梁上，半径为r2。当负刚度机构处于平衡位置时，如图2(a)所示，欧拉梁弯曲变形，其形变作用力不产生竖直方向的分量；当受到扰动偏离平衡位置时，如图2(b)所示，欧拉梁的形变力提供竖直方向的负力，同时欧拉梁的形变减小；当偏离平衡位置的量继续增加，欧拉梁的形变力减到0时，如图2(c)所示，负刚度机构将不提供任何力。

图1 准零刚度弹簧Fig.1 Quasi-zero-stiffness spring

图2 负刚度机构Fig.2 Negative stiffness mechanism

设欧拉梁无形变时，欧拉梁与活塞杆的距离为δ，若在活塞杆上施加力f，使活塞杆产生位移Δl，欧拉梁的形变力通过凸轮施加给活塞杆。此时

f=kΔx-2f1cosα

(1)

其中：f1为凸轮与滚轮的相互作用力；α为力f1与竖直方向的夹角。

由文献[6]可以得到力f1的计算公式为

(2)

将式(2)带入式(1)得

(3)

将式(3)无量纲化为

(4)

(5)

对上式求导，得到无量纲刚度

(6)

(7)

(8)

图3 无量纲力与位移曲线Fig.3 Dimensionless force and displacement curve

图4 无量刚度与位移曲线Fig.4 Dimensionless stiffness and displacement curve

2 可变负载的准零刚度隔振器模型

对于图1所示的准零刚度弹簧，负载的变化必然使隔振器的静平衡位置发生变化，使隔振器的隔振性能变差。为了使隔振器适应负载的变化，设计了如图5所示的隔振器。

图5 可变负载的准零刚度隔振器Fig.5 Quasi-zero-stiff vibration isolator with variable load

该隔振器由准零刚度弹簧、半径为R的滑轨、竖直方向的固定杆和套筒组成。准零刚度弹簧一端固定在套筒上，另一端固定在滑轨上，其与竖直方向的夹角为θ。处于平衡位置时，弹簧长度为R，上下2根弹簧处于旋转对称的位置。负载变化时，可通过改变θ的大小，改变准零刚度弹簧提供的负载力，当θ=0时承载能力最大。若隔振器的最大载重为M，则隔振器理论上可以在0～M之间保持准零刚度的特性，但是随着θ的增加，隔振器的相对位移幅度将减小。

θ=0时，隔振器的最大负载力为

FM=Mg

(9)

若隔振器的负载减小为m时，隔振器提供的负载力为

Fm=FMcosθ=mg

(10)

此时，若隔振器在力FQ下产生位移x，则有

(11)

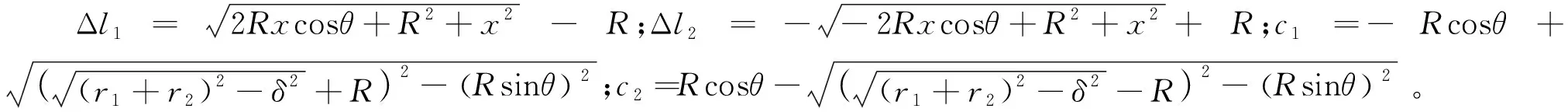
将式(11)无量纲化得

(12)

图6 隔振器的无量纲力与位移关系图Fig.6 The dimensionless force and displacement diagram of vibration isolator

(13)

精确式与简化式的对比如图7所示，实线代表原式(12)，虚线代表化简式(13)。从图中可以看出，三阶泰勒式(13)可较好地表示原式(12)。

图7 精确式与简化式的对比图Fig.7 The precise and simplified type contrast diagram

3 幅频特性分析

本节采用平均法推算了隔振器的主共振响应，并分析参数对振动响应的影响。当隔振器受到基础激励时，振动方程为

(14)

其中：z为被隔振物的位移；y为基础激励位移；m为被隔振物的质量；c为隔振器阻尼；FQ(z-y)为弹性恢复力。

令z-y=x，无量纲化后得

(15)

(16)

整理得

(17)

(18)

(19)

(20)

(21)

解得

(22)

(23)

其中

λ=arccos(c1/A1)。

(24)

为研究隔振参数对相对位移x的影响，令A2=0.1，ξ=0.01，θ分别为0，π/6和π/4，幅频特性如图8所示。从图中可以看出，当θ不为0时，幅频特性具有渐硬-渐软性质，共振段先向右偏，然后向左偏，与普通准零刚度隔振器相比，压缩了共振段的频率范围，减小了最大共振频率。随着θ的增加，共振的峰值减小，共振频率范围向低频方向移动。令ξ=0.01，θ=π/6，A2分别为0.1，0.2和0.3，激励幅值对幅频特性的影响如图9所示，激励幅值越大，向下跳跃频率和向上跳跃频率越大。令A2=0.1，θ=π/6，ξ分别为0.01，0.02和0.03，阻尼对幅频特性的影响如图10所示，与线性系统类似，阻尼比增大可以减小共振峰值。

图8 θ对幅频特性的影响Fig.8 The effect of θ on amplitude-frequency characteristics

图9 激励幅值对幅频特性的影响Fig.9 The effect of excitation amplitude on amplitude-frequency characteristics

图10 阻尼对幅频特性的影响Fig.10 The effect of damping on amplitude-frequency characteristics

4 位移传递率分析

对于基础激励隔振，位移传递率是隔振性能的重要衡量指标。由于z=x+y，设被隔振物的振动幅值为A3，则有

(25)

位移传递率为

(26)

分析参数变化对位移传递率的影响，作式(26)的对数幅频图。令A2=0.1，ξ=0.01，θ分别为0，π/6和π/4，θ对位移传递率的影响如图11所示。从图中可以看出：随着θ的增加，向下跳跃频率和向上跳跃频率均减小，振动峰值也降低；而且θ的增加使振动峰值处具有渐软特性，θ越大，这种特性越明显。在下支的低频段，θ越大，传递率越小，但是随着频率的增加，传递率趋于一致。由此可看出θ的增加对共振有一定的抑制作用，并且可以降低起始隔振频率。

图11 θ对位移传递率的影响Fig.11 The effect of θ on displacement transfer rate

令ξ=0.01，θ=π/6，A2分别为0.1，0.2和0.3，激励幅值对位移传递率的影响如图12所示。随着激励幅值的增加，向下跳跃频率和向上跳跃频率均增加，而且振动峰值处具有渐软特性越加明显。在下支的低频段，激励幅值增大会增大位移传递率，但是随着频率的增加，传递率趋于一致。令A2=0.1，θ=π/6，ξ分别为0.01，0.02和0.03，阻尼对位移传递率的影响如图13所示，阻尼比增大可以抑制共振，但是削弱了非共振段的隔振能力。

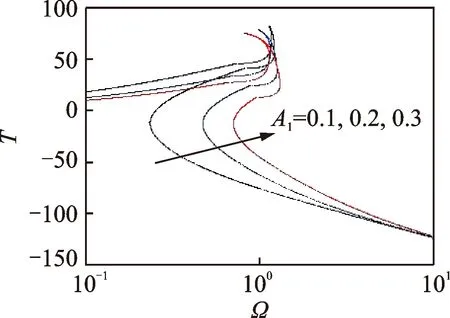
图12 激励幅值对位移传递率的影响Fig.12 The effect of excitation amplitude on displacement transfer rate

图13 阻尼对位移传递率的影响图Fig.13 The effect of damping on displacement transfer rate

5 结 论

1) 笔者提出的隔振器可以通过改变准零刚度弹簧的夹角来适应负载变化，使隔振器在静平衡位置保持准零刚度的特性，解决了负载变化导致隔振性能降低的问题，而且隔振器刚度随着夹角的增加而降低，可以进一步提高隔振器的低频隔振性能。

2) 对于位移传递率，随着准零刚度弹簧夹角的增加，可以降低起始隔振频率，对共振有一定的抑制作用。阻尼比的变化对隔振系统位移传递率的影响与线性系统类似。激励幅值的增加能降低同频率的共振传递率，使传递率峰值向低频方向移动，但同时也增加了低频段的非共振移传递率。

3) 对于相对位移的幅频特性，激励幅值越大，相对位移越大；阻尼增加，共振峰值减小；随着准零刚度弹簧夹角的增加，可以改善共振特性，减小振动峰值，降低起始隔振频率。