基于深度信念网络的磷石膏充填材料强度预测

张安安， 邓芳明

(1.江西省科学院能源研究所，南昌 330029；2.华东交通大学电气与自动化工程学院，南昌 330013)

近年来，随着绿色开采技术的发展，充填材料作为该项技术核心部分，中外研究人员对此开展了研究，如膏体充填材料[1-2]、未分级尾矿材料胶结充填材料[3]、高水充填材料[4]和似膏体充填材料[5]。这些材料中，成本低、流动性好、强度高、污染低的膏体型充填材料最为流行。尹博等[6]对掺入粉煤灰的膏体充填材料水化过程各阶段变化特征进行分析；膏体充填材料的强度主要取决于他的配合比，因此，需得到较高的强度则需要找到最佳的混合比例。

然而，传统计算最佳配比是采取正交试验以及运用理论模型来确定，Ren等[7]采用正交试验设计方法，进行了RPC(reactive powder concrete)配合比设计研究。然而这些实验方法缺点是成本高、耗时长。随着机器学习[8]技术的发展，人工智能算法开始被应用于建筑和矿业工程领域。常庆粮等[9]运用神经网络建立充填材料质量的预测模型；董越等[10]通过正交实验并结合BP神经网络建立充填体强度预测模型；王春雷等[11]针对锂电池基于改进RVM进行寿命预测；张静等[12]采用粒子群算法优化支持向量机对混凝土强度进行预测。但这些方法预测精度较低，需要大量的训练数据和测试数据，导致预测速度较慢。与支持向量机相比，关联向量机的框架更稀疏，核函数约束更少，预测时间更短，当处理具有不确定连接的参数，RVM(relevance vector machine)的预测精度较差。然而相对于RVM、BP(back propagation)神经网络和支持向量机的上述不足，深度学习则具有预测精度高且预测时间快的优势，近年深度学习理论的迅速发展，深度学习方法也被广泛应用于各大领域，自动编码器(AE)、卷积神经网络(convolution neural network,CNN)和深度信念网络(deep belief network,DBN)是应用最为广泛的三种深度学习方法。史杨等[13]提出一种改进自动编码器方法来预测大尺度下土壤有机质含量等级。Jang等[14]运用深层卷积神经网络对混凝土抗压强度进行预测，然而，这两种方法AE易于训练，所需训练数据较少。CNN由于池化层处理会丢失大量有价值信息，忽略局部与整体之间关联性。然而DBN通过训练前的无监督学习，有效地避免了训练数据集的过拟合现象。与传统的无监督学习模型相比，DBN可以获得隐藏在多个特征中的深层规律，并具有较好的泛化能力。Peng等[15]提出了一种基于深度信念网络的无监督健康指标构建方法，并将其与粒子滤波相结合进行建筑剩余寿命预测。

为此，提出一种基于DBN的膏体充填材料强度预测方法,采用量子粒子群算法优化深度信念网络确定DBN的隐含层节点个数和学习率来预测磷石膏充填材料的强度。

1 基本原理

1.1 受限玻尔兹曼机

利用逐层贪婪训练原理，根据受限玻尔兹曼机(RBM)构造DBN模型。RBM模型由可视层v={0,1}D和隐含层h={0,1}K,两层组成，RBM的结构如图1所示。可视层和隐含层都包含一系列单位，输入数据被送入可视层。各层的能量结构如式(1)所示：

图1 RBM结构Fig.1 Structure of RBM

(1)

式(1)中：wpq为可见单位p与隐藏单位q之间的权重;cp和bq分别为可见单位p和隐藏单位q的偏置项；vp为可见单位p的状态；hq为隐藏单位q的状态。 各层的联合概率密度分布为

(2)

式(2)中：Z为归一化常数。从式(1)中可以看出，降低能量可以增加概率。可视层v和隐层h的激活概率可由式(3)～式(5)计算:

(3)

(4)

(5)

采用CD算法权值进行更新，权值的变化量计算公式如式(6)所示:

Δwpq=ε(vphqorigin-vphqreconstruct)

(6)

式(6)中：ε为学习速率hqorigin为隐藏单位的原始状态；hqreconstruct为隐藏单位的重构后状态。每个RBM模型都有自己的学习速度，最优学习速度可以生成合适的权值分布。

RBM的重构过程如图2所示。在这个过程中，隐含层尝试重建一个可视层v1，可视层v1可以恢复原始的可视层v，那么在隐层中得到的数据可以被认为是输入数据的特征。如果重构后的数据能够很好地恢复原始输入数据，则认为隐含层能够有效地从原始数据中学习鲁棒特征。

图2 RBM的重建过程Fig.2 Reconstruction procedure of RBM

1.2 DBN结构

一般来说，单阶段RBM无法实现最优的特征学习性能。因此，将多个RBMs进行叠加，形成一个较深的结构来很好地提取特征。第一个RBM提取的特征被输入到下一个RBM。图3为典型的(两级RBM)DBN的整个训练过程，该过程包括一个预训练和一个微调过程，输出层一般采用Softmax分类器。

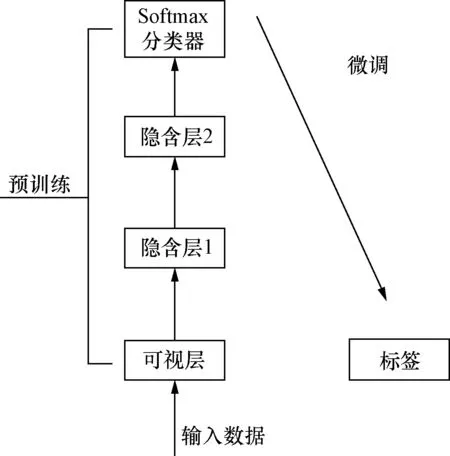
图3 DBN结构Fig.3 The structure of DBN

在训练前的过程中，首先对输入数据进行第一RBM处理，然后将所学习的特征作为第二RBM的输入数据，得到第二RBM的特征。进行反复迭代，最后一次RBM得到的特征是训练前过程中提取的特征。然后，将特征输入Softmax分类器层进行微调。

在微调过程中，利用Softmax分类器对预先训练好的DBN模型进行微调。利用软最大分类器对训练前提取的特征进行分类，生成特征标签。然后，将生成的标签与输入数据标签进行比较，并利用反向传播机制通过更新RBM中的权值来最小化这两种标签之间的误差。在微调过程完成后，最后一个RBM所提取的特征被认为是DBN模型的学习特征。

学习速率和RBM层是DBN模型的重要参数，对DBN的特征提取性能有重要影响。这两个参数都是根据经验来选择的，并不能总是找到最优的结果。因此，采用量子粒子群优化(quantum particle swarm optimization,QPSO)算法来寻找这两个参数的最优值。

1.3 QPSO算法

QPSO算法是将量子行为引入粒子群算法的收敛机制[16]。由于量子行为具有多态性和不确定性,它可以使粒子以一定的概率出现在空间的任何一点上，并且在性质差异上满足聚集态的要求，从而使粒子能够更有效地在整个空间中寻找全局最优解。QPSO算法中的粒子迭代如式(7)～式(9)所示:

(7)

P=μPi+(1-μ)Pj

(8)

Xi(t+1)=P±αmbest-Xi(t)ln(1/u)

(9)

式中：M为人口规模；μ和u的随机数均匀分布区间[0,1]；mbest的平均位置所有粒子的最优位置；Pi和Pj分别为第i和第j个粒子个体最优位置和全局最优位置;X(t)为i粒子的位置在t迭代；α为压缩扩张系数。利用QPSO优化DBN模型的过程可以描述如下。

Step 1初始化QPSO，包括粒子位置、搜索空间、压缩膨胀因子和迭代，将DBN的学习率和隐含层节点数投影为粒子位置。

Step 2计算组中每个粒子的适应度值，然后计算每个粒子的个体最优位置和组的全局最优位置。

Step 3计算所有粒子的单个最优位置的平均值，然后更新粒子的位置。

Step 4重复Step1～Step3，直到满足收敛条件，优化结果为DBN模型的最优学习率。

优化过程中采用的适应度函数为

(10)

式(10)中：RMSE为均方根误差，当得到最大适应度值时，输出结果为学习率的最优解。整个过程如图4所示。

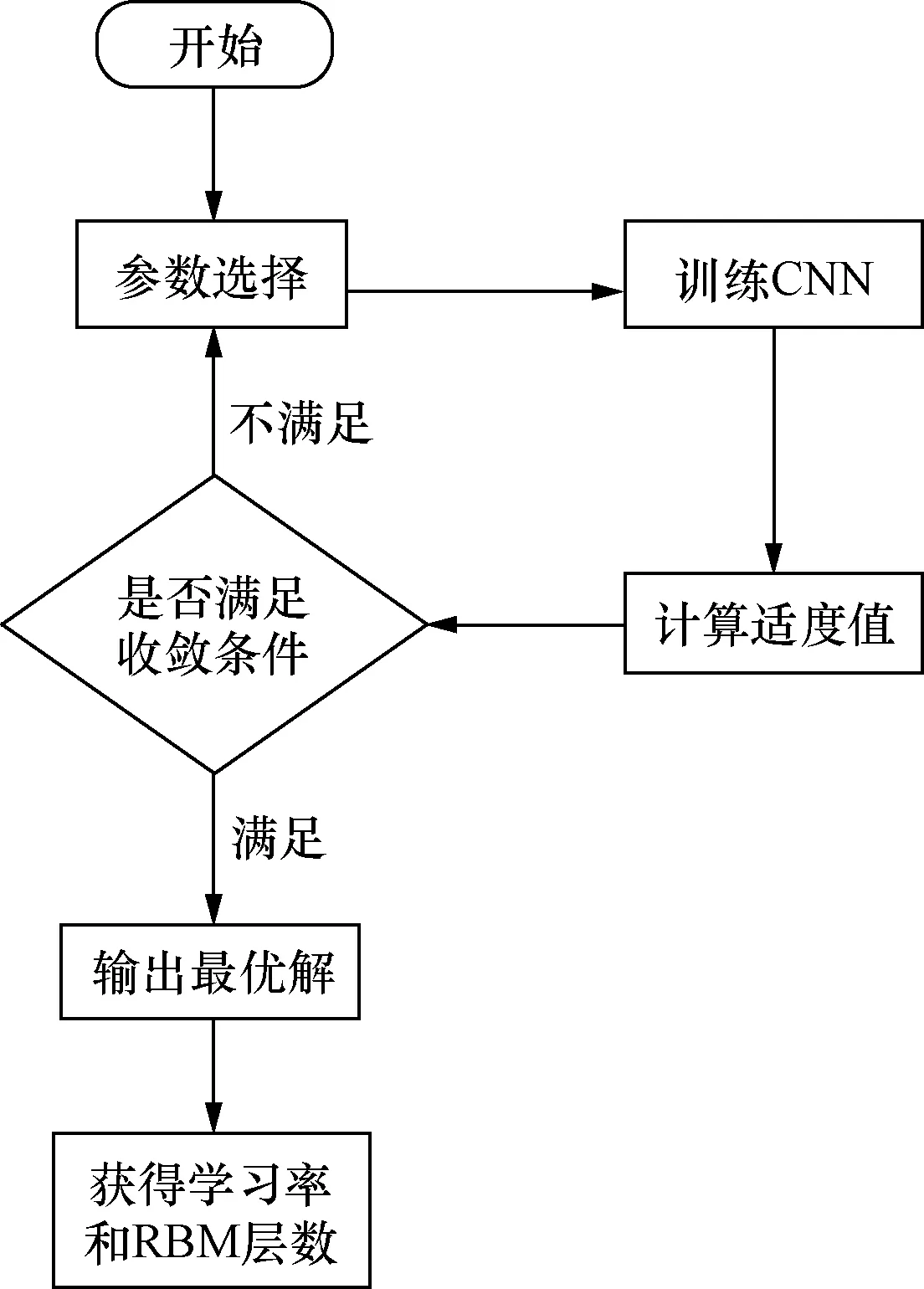
图4 优化学习率流程图Fig.4 The flow chart of optimizing learning rate

2 测试

2.1 原材料选取

由于磷石膏颗粒极其细小，实验测得0.1 mm颗粒占93%，中位粒径为0.043 mm，空隙率和渗透系数较小。这些特点决定了磷石膏不适合充填体脱水和快速硬化。此外，磷石膏中含有 CaSO4·2H2O，占90%以上，具有缓凝性，不适合作为回填材料。但添加粉煤灰和水泥后，磷石膏的性能会发生变化，所以选取以下材料作为实验原材料。

(1)充填骨料:实验采用磷石膏作为充填骨料。

(2)细骨料:采用华能热电厂生产的粉煤灰级作为细骨料。

(3)胶结材料:采用安徽海螺水泥有限公司生产的42.5普通硅酸盐水泥作为胶结材料。

2.2 测试方法

试件体积为70.7 mm×70.7 mm×70.7 mm。待试件完成后，将试件放入设定温度为22 ℃的养护箱中。采用Instron 250 kN试验机对不同龄期的单轴抗压强度、充填材料配比、浓度、强度进行测试，结果如表1所示。值得注意的是，在表1中。D1为水泥比，D2为配比，D3为磷石膏料浆浓度，D4为抗压强度，D5为粒度分形维数，D6为孔隙分形维数。后续作为预测模型的基本数据。

表1 充填材料配比正交试验设计Table 1 Orthogonal test design of filling material ratio

从实验中得出，随着磷石膏料浆浓度的增加，充填材料的强度也会增加。当磷石膏料浆浓度从60%提高到63%时，90 d的抗压强度可提高20%。但由于磷石膏浆液黏度大，浓度高，难以对其进行管道输送，因此，最佳浆液浓度为60%～63%时磷石膏具有较强的流动性，易于实现全管道输送，管道磨损小。粉煤灰具有良好的活化性能，可以降低水泥用量，提高磷石膏充填材料的性能，降低成本。

3 膏体充填材料预测模型

采用参数D1、D2、D3、D5、D6作为输入值，D4(28 d强度)作为输出值。由于两阶段DBN是最常用的模型，采用包含两个RBM的两阶段DBN，每个RBM分别训练。

4 预测结果与分析

实验通过MATLAB 2016a建立了DBN的预测模型。首先选取表1中的10组数据(1～4、7～12)作为训练数据，其余数据作为测试数据。初始化的偏置项设置为0，并随机生成权重分布。DBN的分层训练能够提高训练效率，通过最小化预测值与实际值之间的误差，优化偏置项和权值分布。

实验结果如表2所示。由表2可以看出，对于实验数据集，本文方法对5个指标的预测误差均较小，最大预测误差为2.7%，这对于膏体充填材料强度预测是有效的。利用DBN模型，可以分析和确定充填材料中各变量的影响。

表2 提出方法的预测结果Table 2 Prediction results of the proposed approach

通过搜索DBN的最优学习率和隐含层节点个数来评价所引入算法的优化性能，收敛结果如图5所示。由图5可以看出，QPSO避免陷入局部最优，收敛速度快(37次迭代)，预测精度高(MSE为 0.000 153)，本文优化学习率为0.358，隐含层节点数分别为6和4。

图5 QPSO的收敛性Fig.5 The convergence of QPSO

为了进一步评价优化性能，将优化后的DBN与传统DBN的预测误差进行对比，结果如图6所示。误差由式(11)计算:

(11)

式(11)中：E为总误差；Vp为预测值；Vr为真实值。

从图6可以看出，优化后的DBN预测误差小于传统DBN，在预测开始时，由于历史数据有限，两种方法的预测误差都较高。随着历史数据个数的增加，优化后的DBN误差迅速减小，最终误差为0.001 3。传统的DBN误差下降速度较慢，最终误差为0.475，远高于优化后的DBN。

图6 优化后的DBN与传统DBN的预测误差比较Fig.6 Prediction error comparison of optimized DBN and traditional DBN

并对长期预测精度进行了测量，评价了该方法的性能，测量结果如图7所示。从图7可以看出，在28 d的预测时间内，预测值与实测值具有较高的一致性，最大预测误差为1.66%，说明所提出的预测模型在充填材料强度的长期预测中具有较好的性能。

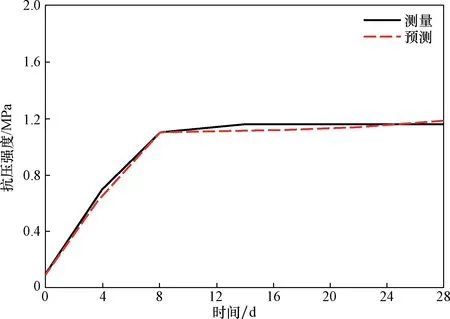
图7 长期预测精度Fig.7 Long term prediction accuracy

对本文方法与传统方法的预测性能进行了比较。分别选取BP神经网络、SVM和RVM构建预测模型。采用这4种模型对充填材料28 d后的抗压强度进行估算，预测时间和精度记录在表3中。从表3中看出，DBN模型预测精度最高，需要的预测时间最少。从测量结果可以推断，提出的DBN模型可以为充填材料元件的优化提供指导，保证煤矿安全环境。

表3 4种模型预测结果比较Table 3 Error comparison of four prediction models

5 结论

充填材料的强度对煤矿的安全生产和可持续发展具有重要意义，但充填材料的组成与强度关系复杂，难以计算。因此，利用能够发现材料构件之间深层连接的DBN及其强度来预测不同构件的充填材料强度。与传统的BP神经网络、SVM和RVM模型相比，DBN具有更好的预测能力，具有更高的预测精度和速度。实验结果表明，所提出的DBN预测模型长期预测的最大错误率为1.66%，需要 1.89 s 的预测时间。这一结果表明，DBN模型能够广泛应用于充填材料的强度预测。