基于全变分模型的多时相遥感影像厚云去除算法
王 睿,黄 微,胡南强
(上海大学通信与信息工程学院,上海 200444)
(*通信作者电子邮箱wr17721415@163.com)
0 引言
光学遥感影像在变化检测、地物分类、环境监测等领域有着非常广泛的应用。遥感数据在成像时,难免会受到云层的影响。云层覆盖区域信息的缺失造成影像质量的退化,降低了遥感影像的利用率。因此,对遥感影像进行去云处理,获取清晰的无云影像,具有非常重要的价值。
针对遥感影像中云层覆盖的问题,国内外的学者和研究人员提出了大量的去除厚云的算法。这些算法大致可以分为3 类[1]:基于图像修复法、基于多光谱法和基于多时相法。基于图像修复的算法通过利用无云区域的信息重建云和云阴影覆盖区域的像素,得到在视觉上令人满意的去云效果,主要通过小波变换[2-3]、支持向量机[4-5]、相似像元替换[6]等方法。由于缺乏充分的辅助信息,易受到图像缺失尺寸大小的影响,当缺失面积较大时,这类方法无法有效地恢复地物信息。基于多光谱的算法通过不同波段数据之间的关联信息对数据进行恢复。Xu 等[7]利用Landsat8 影像的可见光波段与第9 波段和与近红外波段的相关性进行去云。Modis 第6 波段通常是不可用的或带有很多噪声,研究人员利用其他波段数据与第6波段数据的相关性建立函数模型进行信息重建[8-9]。随着遥感技术的发展,获取同一区域的多时相遥感影像成为可能。基于多时相的去云算法是利用其他时相的影像数据作为辅助信息,对大面积厚云覆盖的区域进行信息重建[10]。胡志勇等[11]通过线性回归分析减轻多时相影像之间的光谱差异并增强时相相关性,最后利用影像自身信息进行插值修复云污染区域信息。Zeng 等[12]基于线性回归模型分析多时相数据间的线性关系,以其他时相的图像为参考信息,通过影像间的线性关系估计像素缺失区域的信息并进行替换,最后利用非参考的正则化算法对重建结果进行优化。Cheng 等[13]基于时空马尔可夫随机场(Markov Random Field,MRF)模型替换待恢复影像的缺失像素。Tierney 等[14]基于全变分模型提出了选择多源全变分图像重建(Selective Multi-source Total Variation image restoration,SMTV)算法,将多张含噪或局部信息缺失的图像融合成清晰影像。
虽然现有的算法能够获得较理想的厚云去除结果,但是当获取季节和大气条件不同时,多时相遥感图像存在亮度差异,因此基于多时相影像的厚云去除算法对图像具有较苛刻的时间或季节限制,造成这类算法难以实用。为了解决上述问题,本文提出了一种基于全变分模型的多时相遥感影像厚云去除算法。首先,对多时相遥感图像进行亮度校正;然后利用选择多源全变分图像重建算法对亮度校正后的多时相图像进行重建;最后,对重建图像局部区域利用泊松(Poisson)编辑进行优化,得到最终去云结果。实验结果表明,本文算法能够有效解决亮度信息不一致和边界问题。
1 选择多源全变分图像重建
全变分模型具有非光滑性和不可微分的优点[15],在图像恢复领域有许多的应用。假设待重建图像的成像模型如下:

其中:A、N、I分别表示原始图像、高斯噪声和待重建图像;P表示如模糊等过程的线性算子。
为了恢复图像A,使用下面的凸目标方程:
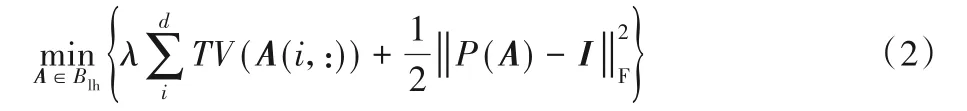
其中:A(i,:)是原始图像A的第i行像素;TV(A(i,:))为离散全变分;Blh为边界条件。

全变分变换可以分为两种类型:各向同性和各向异性。各向同性的全变分变换定义为:

各向异性的全部变分变换定义为:

其中:bx,y是图像b在(x,y)处的像素值。当x=m+1 和y=n+1时,超出了图像的边界,故全变分变换存在下面的边界条件:
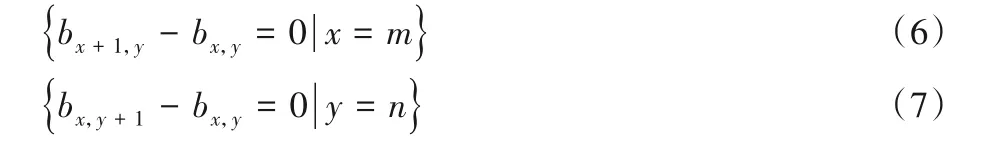
各向异性全变分变换与各向同性全变分变换相比,重建图像具有更好的恢复质量,故在求解方程时,采用各向异性全变分变换。全变分图像重建算法能够对部分信息丢失的影像进行恢复,但是当局部信息完全丢失时便无法适用。当信息完全丢失时,需要借助其他辅助图像信息进行重建。文献[14]提出的选择多源全变分图像重建算法利用多幅图像的数据信息互补进行图像重建,能够有效解决这个问题。式(2)变为:
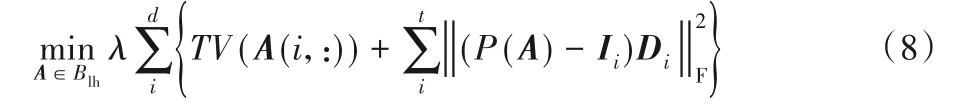
其中:Ii为第i幅待重建图像;Di为Ii的已知损坏像素的对角矩阵,对角矩阵的值为0 和wi,wi是分配给该图像的权重,一般可设为1。通过Di可以主动选择需要忽略的损坏或不需要的像素点,并且同时考虑了多幅影像间的相互影像,甚至是每个像素点的相互影像。对式(8)进行求解,便可以得到重建结果。
SMTV 算法对多时相遥感影像的去云结果如图1 所示。图1(a)、图1(b)、图1(c)为不同时间段获取的局部厚云覆盖的遥感影像,它们的厚云覆盖区域位置和大小不同,无云区域的亮度信息基本相同,重建结果如图1(d)所示,重建图像质量很好。图1(e)、图1(f)、图1(g)为另一组遥感影像,与第一组不同,它们的无云区域的亮度差异较大,导致重建图像的质量急剧退化,存在区域亮度不一致和明显的边界问题(如图1(h)所示)。

图1 SMTV算法去云结果Fig.1 Cloud removal results of SMTV algorithm
2 本文算法
针对上述亮度差异造成的区域亮度不一致和明显边界问题,本文对多时相图像进行亮度校正预处理,并利用泊松图像编辑对经选择多源全变分重建算法处理后的结果中亮度不一致区域进行优化,有效改善了重建图像质量。下面从亮度校正和泊松图像编辑两个部分详细介绍本文算法。
2.1 亮度校正
虽然多时相遥感影像的厚云覆盖区域的位置和大小不同,但是它们的无云区域存在共同区域,可以利用该区域的亮度之间的关系对图像亮度进行校正。本文利用掩膜函数算法(Function of mask,Fmask)[16]对厚云进行检测,将厚云覆盖区域记为0,无云区域记为1,得到厚云分布掩膜。共同区域的像素集为:

其中:x代表像素坐标位置;P1是一幅遥感影像的无云区域像素集;P2是另一幅影像的无云区域像素集;Pf为共同遮挡的像素集。
完全无云的图像可以保证与同组的所有图像存在共同区域,以该无云影像的亮度为标准亮度,可以完成同组其他图像亮度的校正,使其尽可能与标准亮度相近,从而减小多时相影像间的亮度差异;但是遥感卫星在获取数据时无法避免地会受到云层的影响,所以该方法存在很大局限性。为了解决多幅有云遥感影像的亮度校正问题,提出了以校正系数为基准的动态校正方法。本文选取同组无云覆盖区域面积最大的图像的亮度作为标准亮度,其他图像以此亮度为亮度标准进行校正。校正系数定义为图像与标准亮度图像在共同区域像素集的比值:
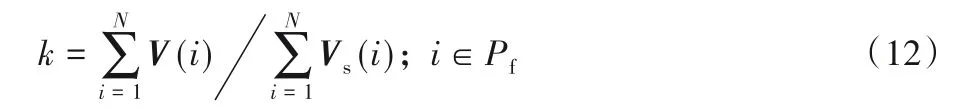
其中:N为像素集的大小;V和Vs分别为该图像与标准图像。当输入图像与标准图像存在共同区域时,通过式(12)计算校正系数。当输入图像与标准图像不存在共同区域时,选取已计算得到校正系数的图像作为参考标准进行计算:
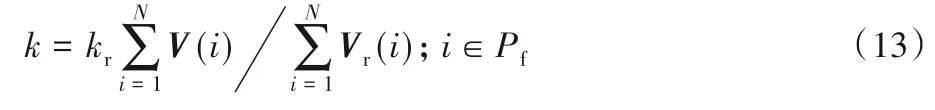
其中:kr为参考校正系数;Vr为参考图像。
计算得到校正系数,对图像的亮度进行校正:

本文对多时相遥感影像的各个波段进行亮度校正后,基于选择全变分模型进行重建,得到初始的重建图像。
2.2 泊松图像编辑
亮度校正有效改善了重建图像中亮度信息不一致问题,但是当无云区域仅存在一幅遥感影像中时,根据式(8),重建图像的亮度会尽量与该图像保持一致,从而造成局部区域亮度不一致。因此本文利用泊松编辑对存在这一问题的重建图像区域进行了优化。泊松图像编辑算法能够根据所指定的边界条件,求解泊松方程,实现重建图像边界梯度上的连续[17]。
根据泊松图像编辑的思想,对重建图像的局部区域进行优化。首先,获取每幅图像的掩膜信息,云层覆盖区域记为0,无云区域记为1。对掩膜的数值进行计数,统计同组多时相遥感影像中仅出现过一次的区域:

其中:x为像素点坐标位置;Mi为第i张图像的掩膜;N为多时相遥感影像的数量。M中数值为1 处即为所有图像中仅出现一次的区域,如图2 所示。图2(a)、图2(b)、图2(c)为每幅图像的掩膜,图2(d)为仅出现过一次的区域。

图2 仅出现一次区域计算结果Fig.2 Calculation results of areas only appearing once
泊松编辑需要输入编辑区域的边界。已知待编辑的区域为G,该区域的边界可以通过式(16)计算:

其中:G1为膨胀处理结果(如图3(a));G2为腐蚀处理结果(如图3(b));C为获得的编辑区域的边界(如图3(c))。
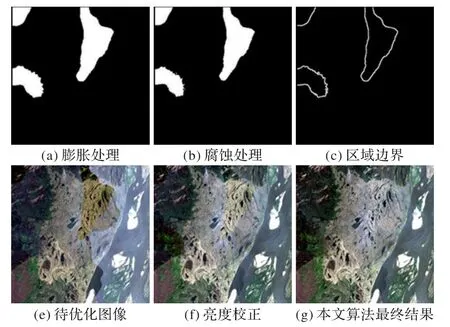
图3 本文算法的各步骤处理结果Fig.3 Results of each step of proposed algorithm
边界的外部图像的目的区域、内部的待编辑的图像区域、区域边界构成了泊松图像编辑模型的要素。以重建图像、区域边界作为输入,得到最终优化结果。图3(d)、图3(e)、图3(f)分别为待优化图像、亮度校正结果、本文算法最终结果。由图3 可以看出,本文提出的算法有效地解决了重建图像中存在的区域亮度信息不一致和边界问题。
3 实验与结果分析
本文选取了四组不同具有代表性地理特征的遥感图像进行实验,其中:图4、图5和图7为landsat8数据,图6为landsat7卫星数据,影像大小均为400×400。为了验证本文算法的有效性,将其与SMTV 算法和文献[11]算法对于四组遥感图像的去云结果进行了比较,如图4~7 所示。实验软件为Matlab R2018a,计算机配置如下:处理器为Intel Core i3-2384M @2.30 GHz,RAM为8 GB,系统为64位Windows 10家庭版。
第一组多时相遥感影像为山区图像,包含大量植被和裸土,数据获取时间分别为2015 年5 月20 日、2017 年6 月2 日、2017 年5 月17 日,分别如图4(a)、图4(b)和图4(c)所示。图4(d)为SMTV 算法去云重建结果,存在大量因亮度不一致造成的明显边界。图4(e)为文献[11]算法去云重建结果,虽然也存在亮度不一致问题,但是重建效果明显优于SMTV 算法。本文算法还原了植被和山地信息,植被色彩真实,山脉的走势和轮廓细节均能较好体现,去云重建结果最优,如图4(f)所示。

图4 山区图像去云重建结果Fig.4 Reconstruction results of cloud removal for mountain area images
第二组多时相遥感影像为城市区域数据图像,包含城区、河流和绿地,数据获取时间分别为2016年8月21日、2018年8月5 日、2017 年8 月24 日,如图5(a)、图5(b)、图5(c)所示。从图5 结果可以看出,当云量较少时,每种算法都可以获得较好的去云重建结果,但是SMTV 算法和文献[11]算法在图像的右上方的河流区域仍存在少许亮度不一致区域(如图5(d)和图5(e)所示)。图5(f)为本文算法处理结果,可以发现,整个河流区域的亮度基本保持一致,有效改善了上述问题。
第三组多时相遥感影像为山脉图像,主要地理特征为山脉和沟壑,数据获取时间分别为2001 年4 月26 日、2002 年8月10 日、2002 年12 月9 日,如图6(a)、图6(b)、图6(c)所示。SMTV 算法结果中存在明显亮度差异,如图6(d)所示;文献[11]算法重建结果整体质量较好,存在局部过渡不自然的情况,如图6(e)所示;本文算法处理结果地物对比度较高,山脉、沟壑之间过渡自然,如图6(f)所示。
第四组多时相遥感影像为平原田地图像,包含田地、河流和房屋,数据获取时间分别为2014 年8 月13 日、2013 年8 月16 日、2013 年9 月11 日,如图7(a)、图7(b)、图7(c)所示。SMTV 算法和文献[11]算法处理结果中均存在块状亮斑,本文算法结果不存在亮斑问题,并增强了原图中的地物特征。由以上实验结果对比可知,本文的改进算法能够有效消除多时相遥感影像恢复时亮度差异对去云结果的影响。

图5 城市区域图像去云重建结果Fig.5 Reconstruction results of cloud removal for urban area images
为了定量地评估去云图像质量,本文采用标准差(STandard Deviation,STD)作为评估因子。STD 能反映图像像素值相对于均值的离散程度,标准差越大,表明图像中灰度级分布越散,图像质量越好[18]。标准差统计结果如表1所示。
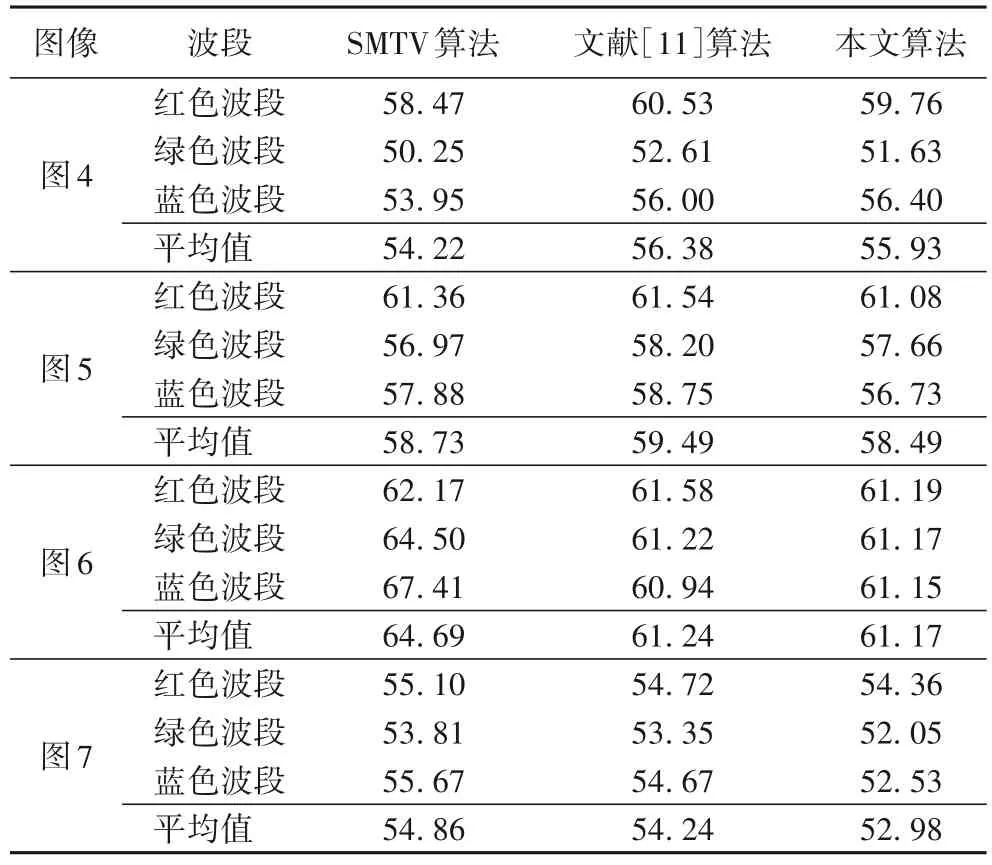
表1 不同算法的标准差统计值对比Tab.1 Comparison of STD statistics of different algorithms
为了定量地评估重建结果的细节反差和纹理变换特征,本文采用平均梯度(Average Gradient,AG)作为评价指标。图像的平均梯度越大,图像的细节反差和纹理变换特征效果越好[18]。平均梯度统计结果如表2所示。
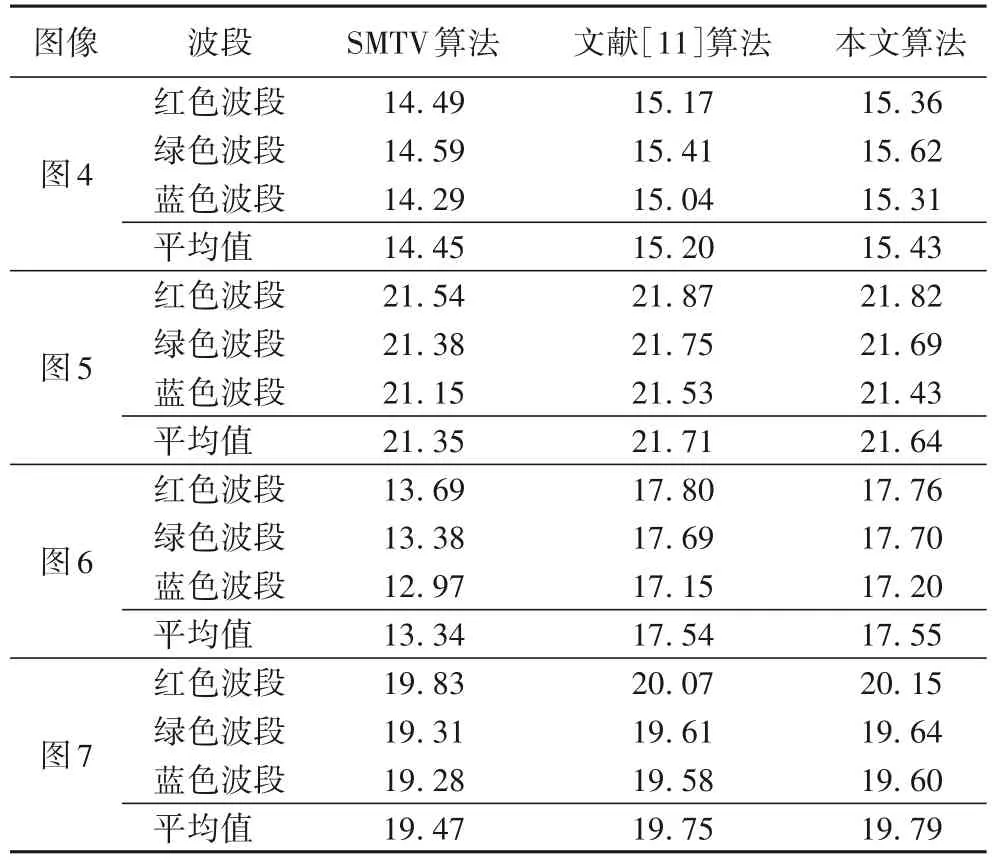
表2 不同算法的平均梯度统计值对比Tab.2 Comparison of AG statistics of different algorithms
由表1和表2的数据可知,三种算法的标准差统计数据差异不大。当结果中存在较大亮度差异时,SMTV 算法的标准差最大,这是由于局部过亮造成的,从重建图像结果可以发现,此时图像视觉效果较差。文献[11]算法和本文算法的标准差数据接近。平均梯度数据统计结果中,本文算法结果的AG 值是最优的,SMTV 算法的AG 值最低。结合视觉分析和定量分析结果可知,本文算法不仅有效解决了重建图像中的亮度不一致和边界问题,而且有效地提高了图像的质量,增强了图像的细节反差和纹理变换特征。
同时,对算法的复杂度进行分析,分别统计了三种算法对每组图像的处理时间,算法时间复杂度统计结果如表3所示。

表3 时间复杂度统计分析 单位:sTab.3 Statistical analysis of time complexity unit:s
由表3 数据可知,本文算法效率要优于文献[11]算法。与SMTV算法相比,本文算法在SMTV算法的基础上增加了亮度校正和泊松编辑优化部分,耗费时间增加了大约三分之一;但是本文算法以增加算法时间复杂度为代价,提高了重建图像的视觉效果,改善了图像细节和纹理变换特征,算法执行时间有所增加是可以接受的。
4 结语
本文提出了一种基于全变分模型的多时相遥感影像厚云去除算法,不仅能够解决多时相图像重建后的亮度信息不一致和边界问题,而且能够有效提高图像质量,增强图像的细节反差和纹理变换特征。本文算法主要分为三步:首先,对多时相遥感影像进行亮度校正;然后,基于全变分模型对校正图像进行重建;最后,对重建图像的局部区域进行优化,得到最终去云结果。实验结果表明,本文提出的算法能够有效解决亮度不一致和边界问题。本文算法适用于利用多时相图像重建一幅无云图像,如何利用多时相图像对指定场景进行信息重建,提高重建图像的保真度,同时提高算法效率,将是后续的研究工作。

