基于循环神经网络的正交网格的自动化生成算法

黄中展，徐世明

（清华大学地球系统科学系，北京 100084）

（*通信作者电子邮箱xusm@tsinghua.edu.cn）

0 引言

动画电影技术、天气预报、工业制造等多个与人们生活息息相关的领域都离不开科学计算，随着这些领域对高质量计算的需求的增大，对数值算法的要求也随之增大。一般来说，在科学计算当中，主要采用的三类数值算法分别为有限差分方法［1］、有限体积方法［2］以及有限元方法［3］。它们广泛地应用于各类计算当中，而这些方法的有效实施离不开高质量的离散化方案，即网格的划分。

在不同的应用场景，网格有很多不同的类型，可从网格形状、目标区域类型、目标区域的维度三个方面来划分。如图1（a）和图1（b）分别展示了二维平面和三维空间中的正交网格样例。

对于二维平面上的网格，除了在图1（a）中所展示的四边形网格之外，还有如图2 所示的三角形网格。相较于四边形网格，三角形网格的生成相对容易。另外，图1（a）中的网格和图2中的网格还有一个显著的差异在于其目标区域的连通性上，图2 所展示的目标区域是多连通区域。多连通区域相对于单连通区域而言，在实际生活和科学计算需要中更为普遍，但是同时网格生成难度也更大，特别是正交网格。

图2 多连通区域的三角网格［6］Fig.2 Triangular grid of multiconnected region

对于平面上的目标区域，三角网格和四边形网格的算法都均可以对目标区域进行离散化。三角形网格主要采用的是Delaunay 三角剖分法［7］、四叉树法［8］以及波前法［9］，其中Delaunay 法使用最为普遍，这是由于它在数学上十分成熟，具有较好的网格质量且收敛性也能较好地保证；而四边形网格的生成主要有格栅法［10］、拓扑分解法［11］、节点连接法［12］等。在天气预报、气候模拟等科学领域中，正交网格应用最为广泛，本文主要考虑的是正交网格的自动化生成。

对于单连通区域的正交网格生成来说，利用Thompson 微分方程法［13］最为普遍，然而这类方法产生的网格在边界处正交性保持较差，收敛性也不能保证，且具有较多的需要调节的参数，这使得当遇到较复杂的目标区域的时候，需要有较多的人工调节，不便于科学计算的实际应用。快速且自动化的生成算法在各种科学计算领域当中十分必要。

1 正交网格的自动化生成

接下来，介绍如何利用循环神经网络和复分析知识来完成正交网格的自动化生成。首先，介绍正交网格生成所需要的基本知识，即共形映射和相关网格生成工具。然后利用这些方法将正交网格问题转换为一个最优化问题，同时介绍利用长短期记忆（Long Short-Term Memory，LSTM）网络［14］来降低最优化问题求解时的时间复杂度，从而能自动化地生成目标区域的正交网格。

1.1 Schwarz-Christoffel共形映射

在复分析中，斯瓦茨-克里斯托弗尔（Schwarz-Christoffel，SC）共形映射是多边形区域中常用的保角映射［15］。SC映射是从一个简单多边形（即不自交的多边形）区域到复平面中的上半平面H={ζ∈C：Imζ＞0}的一一映射方式。另外SC 映射具有显式表达式，考虑n个顶点的简单多边形区域(vi，αi)，i=1，2，…，n，那么H到该区域的SC映射f可以由

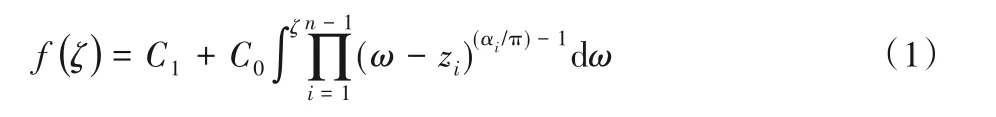
给出。其中：C0和C1为常数，z1，z2，…，zn-1为复平面中实轴上的n-1 个实数，这些实数满足如下对应关系f(∞)=vn和f(zj)=vj(j=1，2，…，n-1)。

共形映射具有一一对应且保持角度这两个良好性质，这些性质可以用于正交网格的生成。如图3 所示，若区域B为目标区域，即需要在区域B当中生成正交网格。可以首先利用SC 映射建立区域B到区域H的共形映射g。若可以建立一个简单的、容易构造正交网格的区域，如区域A，同样利用SC映射可以构建从区域A到区域H的共形映射f，注意到g具有一一映射的性质（具有可逆性），可以建立从区域A到区域B之间的共形映射f⊙g-1，而由保角性，区域A的正交网格可以保持到区域B中，由此得到目标区域B的正交网格。这就是利用共形映射构造目标区域正交网格的基本思路。

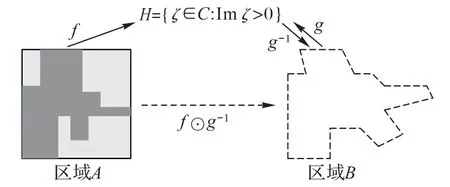
图3 基于SC映射的正交网格生成Fig.3 Orthogonal grid generation based on SC mapping

1.2 Gridgen-c网格生成工具

基于SC 共形映射构造正交网格的理论相对完备，但是在实际网格生成应用以及算法上仍有很多不足。在众多基于共形映射的网格生成工具中，Gridgen-c 工具是基于C 语言的正交网格生成工具，具有快递且稳定的网格生成能力。其不足主要在与需要人为给定目标多边形的转角类型，利用这些人为标定的转角类型，从给定的目标区域B中人为地构造出图3中的区域A。具体来说，如图4所示。

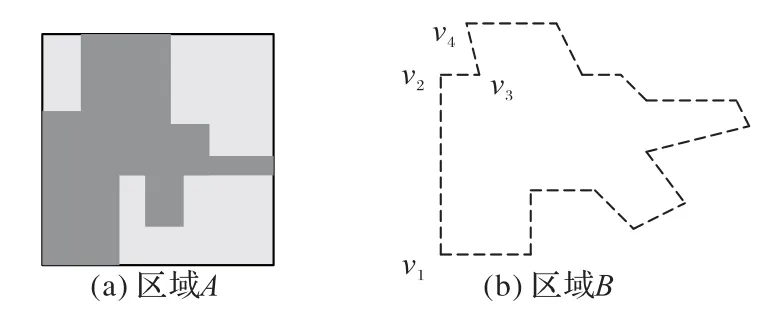
图4 Gridgen-c网格生成工具Fig.4 Grid generation tool Gridgen-c

给定目标区域B，和三种转角类型。Gridgen-c 需要人为提供先验信息，如图4 的区域B中，只需要令以及等（对应图4 区域A的转角类型），就能根据这些给定的转角类型直接构造如图4 所示的区域A。特别地，区域A中的多边形区域实际上只需要通过简单的经纬网（水平、竖直两个方向）即可构造正交网格。利用图3中的流程便可以完成正交网格生成。注意到，如果对于只有少数顶点个数的多边形，通过人为地给定转角类型，可以轻松地使用Gridgen-c 得到正交网格。然而在科学计算的实际具体问题中，如计算机图形学中需要对一定区域进行流体模拟［17］；海洋科学中需要对一定海域做温度计算［18］等，这些具体问题所考虑的多边形区域往往具有较多的顶点个数。若此时，直接对这样的多边形进行人为的顶点转角类型标定的话：一方面将消耗大量的时间；另一方面，对于多顶点的多边形转角标定时，由于人的能力有限，人为的先验信息可能无法给出一个较优的转角标定。针对这样的问题，下面将结合Gridgen-c和深度学习的办法给出一种正交网格的自动化生成算法。

1.3 正交网格生成对应的最优化问题

本节首先对正交网格生成问题建模，即将利用Gridgen-c所需的条件将正交网格的生成问题转换为一个带线性限制条件的整数规划问题。

不妨设对于目标N多边形(vi，αi)，三种转角类型的个数分别为m，p以及q。于是由简单多边形的内角和公式有：

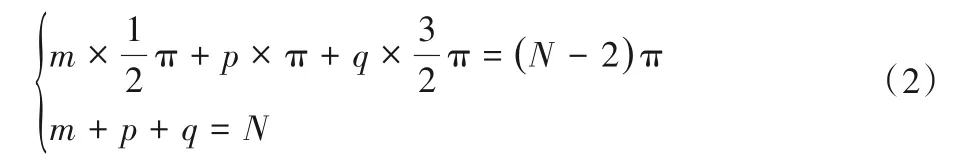
从式（2）可以化简得到-q+m=4，即：

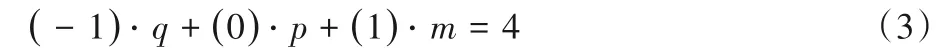
为叙述方便，不妨设N个关于多边形每个顶点的新的变量xi(i=1，2，…，N)，其中对所有的xi满足：

结合式（3）即知xi中分别有q，p，m个的大小为-1，0，1。

在使用Gridgen-c 工具生成正交网格的时候，人为地为目标多边形区域标定每一个顶点的转角类型的时候，必须满足式（4）的限制。换言之，对于一个目标多边形，其各转角类型的选择方案必然对应式（4）的一个解。规定好转角类型后，接着着手设计最优化目标。可以从三个角度来考虑生成的网格的品质的好坏，分别是正交性、均匀性、覆盖性。

正交性 顾名思义即为通过数值方法得到的网格，在各个网格点中正交的程度。从复分析的理论上看，由如图3中f⊙g-1得到的区域B中的网格应该是严格正交的，但是由于数值误差，算法稳定性等问题可能会导致在实际数值算法所生产的网格的正交性不是十分严格，特别是在边界上。

均匀性 生成的网格应保持足够均匀，否则容易产生极端的网格点分布，尽管这些网格点所构成的网格的正交性可能可以保持足够好，但由于网格不均匀所导致的尺度差异，一定程度上不利于其实际的科学计算，可能会产生较大的数值误差等问题。

覆盖性 这里所说的覆盖性是指生成的网格能足够好地覆盖目标区域。在使用Gridgen-c 工具产生正交网格时，目标多边形的顶点转角的错误的标定容易造成所生成的网格的区域较小无法覆盖目标区域，从而不能足够好地满足科学计算中的计算需求。

结合式（4）和上述正交性、均匀性和覆盖性的考虑，可以构造如下最优化问题：

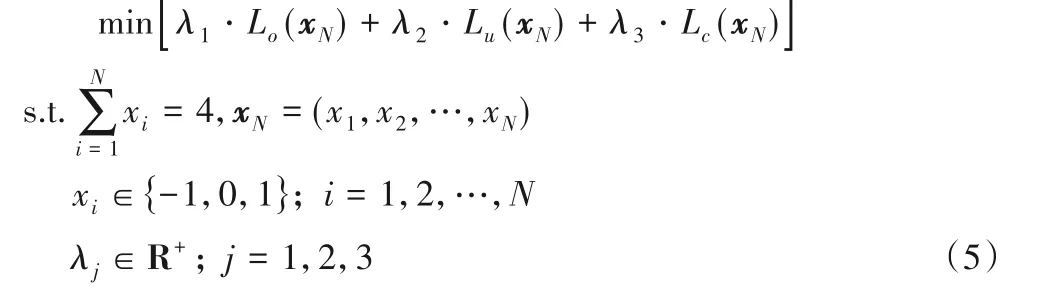
其中Lo(xN)刻画的是网格的正交性，即

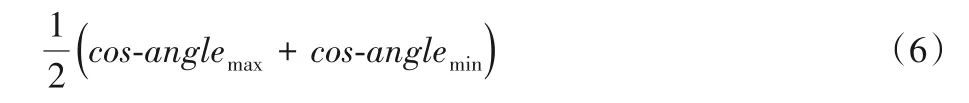
cos⁃anglemax和cos⁃anglemin表示各个网格点中夹角（锐角）余弦值的最大和最小值。容易知道，当Lo(xN)越小时，各网格点处能较好地垂直。另外Lu(xN)表示网格的均匀性，即

areamax和areamin分别表示网格最大和最小面积，当Lu(xN)越小时，网格的最大和最小的面积越接近，即网格的面积大小越均匀。而Lc(xN)表示的是网格的覆盖性，利用式（8）定义：

其中：Area(grid)表示的是生成网格的覆盖面积，而Area(O)表示的是目标区域的面积。注意到，平面上的正交网格生成问题实际上即多边形区域上的正交网格生成问题，均可以通过对式（5）进行求解获得合适的正交网格。为了进一步验证式（5）的通用性，在第2 章中将对三种不同类型的区域验证算法的有效性。在算力允许的情况下，直接遍历式（4）就可以求解该最优化问题。但是实际上，最优化问题（5）是一个带线性限制条件（式（4））的整数规划问题，这是一个NP-hard 的问题，理论上只能通过枚举来获得最优解，而遍历式（4）就至少需要O(3N)的复杂度消耗，由于是指数级复杂度，当N稍大的时候就使得问题几乎不可解。注意到最优化问题（5）的优化目标并不具有良好的可导性和连续性，这使得一些有效的整数规划问题的求解器［19］不能用来对其进行求解。

针对最优化问题（5）时间复杂度过高的问题，提出了利用循环神经网络构建一个关于转角选择的分类器来降低时间复杂度，从而获得较优近似解的办法。

1.4 循环神经网络

为了可以利用循环神经网络来降低最优化问题（5）求解的时间复杂度，此处提出一个基本假设：

基本假设 一个顶点的转角类型取决于其邻近点的转角类型，且越接近的顶点影响越大。

科学计算中所考虑的目标区域多是自然形成的边界，如海岸线、湖泊、动画人物等构成的多边形。这些多边形的边界较为自然，若不满足基本假设，那么它的顶点转角相对独立，边界一般不太符合自然规律。若基本假设成立，那么对于目标多边形的任意一个顶点vi，其转角类型xi取决于其附近的多边形的局部信息，即由vi+1，vi+2，…，vi+t以 及vi-1，vi-2，…，vi - t这些顶点序列构成的某种特征来决定。

接下来利用顶点的两类信息来构造特征：一方面是角度信息，用A(vi)表示顶点vi的内角的余弦值，即向量和向量构成的夹角（内角）的余弦值；另一方面是长度信息，即向量和向量的模长的均值，用L(vi)来表示。但是注意到，实际上L(vi)是无界的，需要进行归一化，即

由此，对于每一顶点vi，都可以构造如下特征

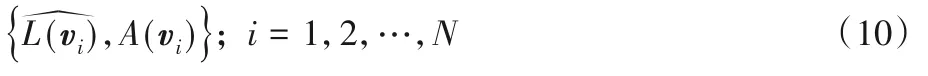
接着考虑较小规模的多边形，如N=10，实际上可以直接对最优化问题（5）进行枚举求解获得最优转角类型。也就是说对于顶点个数为10 的多边形，可以先由式（10）获得特征集，然后通过枚举直接求解得到每个顶点的最优转角，然后利用深度学习的方法来建立特征集到最优转角的映射。

长短期记忆（Long Short Term Memory，LSTM）网络是循环神经网络中最著名的扩展［14］，具有很强的捕获序列之间的信息的能力。由基本假设，多边形任一顶点的转角类型取决于邻近顶点的特征构成的序列，故此处适合采用LSTM 来学习特征集到转角类型的映射。具体而言，如图5 所示，对于N=10时，第t步的更新计算公式为：

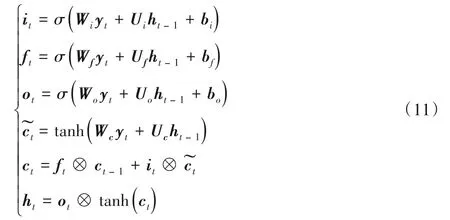
其中，W、U和b是LSTM 各个门的参数。ct为第t步中LSTM 的记忆单元，ht为其隐含层的输出，首先初始化ct和ht，即h0=0以及c0=0。接着，以顶点vi为例，LSTM 的第1步的输入y1为，接着第2步的输入y2为，类似地，第3 步的输入y3为，第4 步输入为，如此类推，一直到第10步。由此，对于N=10 的情况，可以由LSTM 训练得到一个能判断目标多边形转角类型的分类器，即给出各顶点在三种转角类型的概率。注意到，由基本假设，实际上一个顶点的转角类型只和其附近的顶点信息有关，这意味着对于一个M边形，其中M≥N，需要判断其中一个顶点的转角类型，可以只利用上其邻近的顶点信息，如10 个顶点的信息，由此可以用上在N=10时训练出来的分类器来解决M边形的网格生成问题。

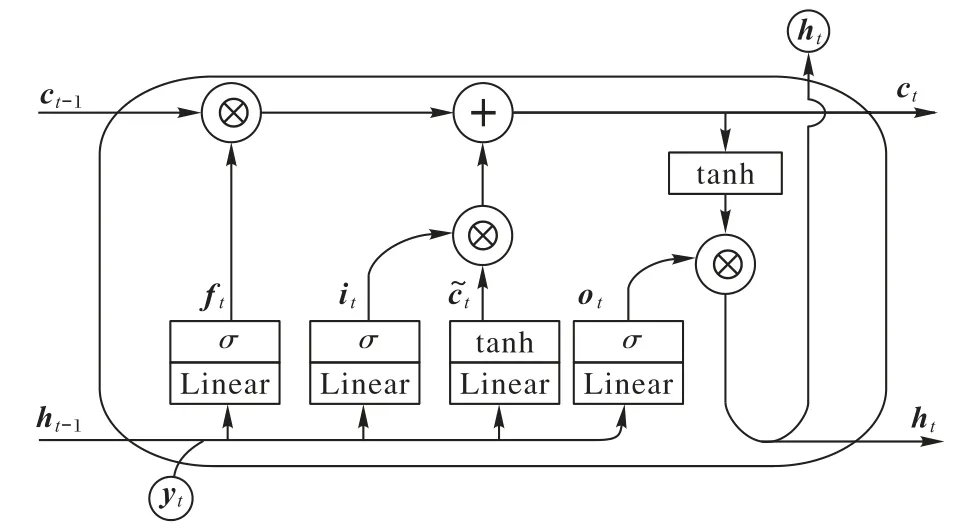
图5 LSTM结构Fig.5 Structure of LSTM

但是如果仅仅依靠分类器来进行转角类型的判断，由于分类器存在误差，得到的解不一定能满足式（4），即使能满足，得到的网格质量不一定能足够地好（取决于转角分类的质量）。面对这样的问题，可以引入一定量的枚举，将LSTM 作为一种降低时间复杂度的工具。

1.5 降低时间复杂度

由于训练数据或者算法的不足，导致LSTM 分类器的性能存在一定的误差，直接使用LSTM 来求解最优化问题（5）很可能会有无解或者解的质量不高的问题。引入一定量的枚举能够缓解这两个问题。

如图6 所示，采用一种简单的策略，对于一个N多边形的一个顶点，首先可以利用由10 多边形训练得到的LSTM 分类器来对其顶点类型进行判断，即得到三种转角类型{0，-1，1}的概率P，给定阈值P0。用两个例子来说明图6 的算法流程，如P0=0.6，当转角概率P={0.7，0.1，0.2}时，此时P最大的概率max(P)为0.7，大于P0，此时可以直接确定转角类型，即此时转角类型为0。如当P={0.5，0.3，0.2}时，此时最大的概率为0.5，比P0小，此时分类器没有足够的把握判断目标多边形的该顶点的转角类型，于是，可以不考虑概率最小的类型，即类型1，仅仅只考虑较大概率的两种转角类型。

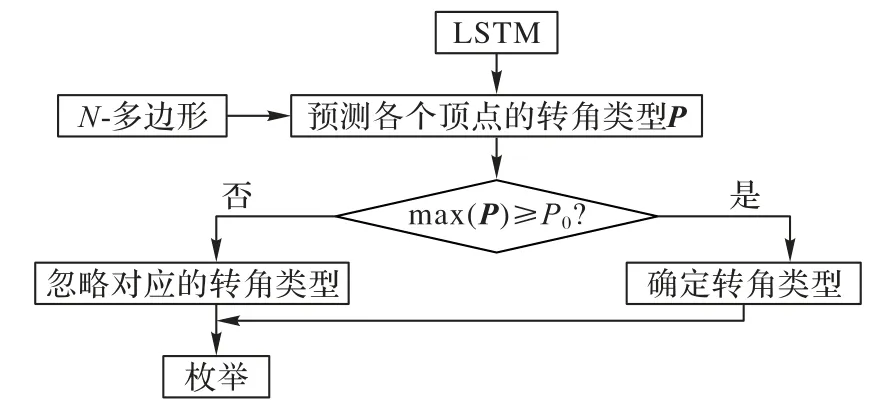
图6 利用LSTM降低时间复杂度Fig.6 Reducing time complexity by LSTM

一般来说，最优化问题（5）的求解至少需要的O(3N)时间复杂度。若利用图6 所示的策略，有L个顶点可以直接确定（即转角类型的最大概率大于阈值P0），此时时间复杂度降为O(3N-L)，而剩下的顶点都不考虑概率最小的情况，此时时间复杂度进一步降低为O(2N-L)，一般来说当L稍大的时候，该计算消耗是可以承受的，L的大小取决于LSTM 的分类能力和阈值P0的选取。由此，通过图6的策略，可以完成的N多边形（其中N≥10）的正交网格的自动化生成。

1.6 训练数据

实际上，为了得到足够好的LSTM 分类器，需要较大数量的多边形样本，其中这些多边形的边界还需要满足一定的物理意义。也就是说，训练集中的多边形不能有过于复杂的边界，否则一方面可能最优化问题（5）没有足够好的解，另一方面较差的解会给分类器的训练引入较大的噪声，降低分类能力，不利于计算复杂度的降低。注意到GADM［20］数据库中有全球各国各行政单位的地理边界数据。该数据集数据量大，且这些地理边界多具有较自然的边界，较为符合基本假设的要求，恰好可以用作此处LSTM 分类器的训练。为了得到合适的训练集，至少做如下3个预处理。

1）保证所考虑的多边形是简单多边形。如果训练数据中含有非简单多边形容易产生较大的数值错误，对模型的训练注入较大的噪声。

2）保证考虑的多边形是单连通区域。在GADM数据集中包含很多群岛等地理边界，这些边界本身就构成了多连通的区域，这些数据应该被预先剔除。

3）由于LSTM 分类器的训练需要的多边形的顶点个数为10，所以对于GADM 数据集中的多边形，可以对其顶点做采样，获得10 边形。然后根据式（10）得到对应的特征，且利用式（5）直接枚举出最优解，作为训练数据。

2 实验与模型分析

本章将通过四个样例来观察生成的正交网格的质量。首先考虑的是两个简单形状的图形，即如图7（a）所示的每一个转角都是90°或者270°的图形。这样的图形能通过简单的纵横划分（经纬网）来获得正交网格。

接着，图7（b）所示的图形是正16 边形，实际上它比较接近一个圆形。实际上，由于其对称性，它的每一个点的转角类型应该都是要相同的，然而由于式（4）的限制，它的各点转角类型不可能完全一样，所以这样的目标多边形区域本身不存在像图7（a）这样足够好的解。从实验结果来看，图7（a）所示的图形生成的正交网格恰好是通过纵横划分获得的，达到7（a）所示图形的网格生成的最优解。如果直接利用Gridgen-c工具和人工选择转角类型，最好的方式也是将90°的转角设为转角类型1，将270°的转角设为转角类型-1，也就是说本文的方法在此样例上达到了最优解。另一方面，尽管正多边形这样的图形在生成正交网格的问题上存在客观的困难，但从图7（b）所示的正16 边形来看，生成的网格已经足够地好，与直接人工进行转角类型选择所生成的正交网格一致。

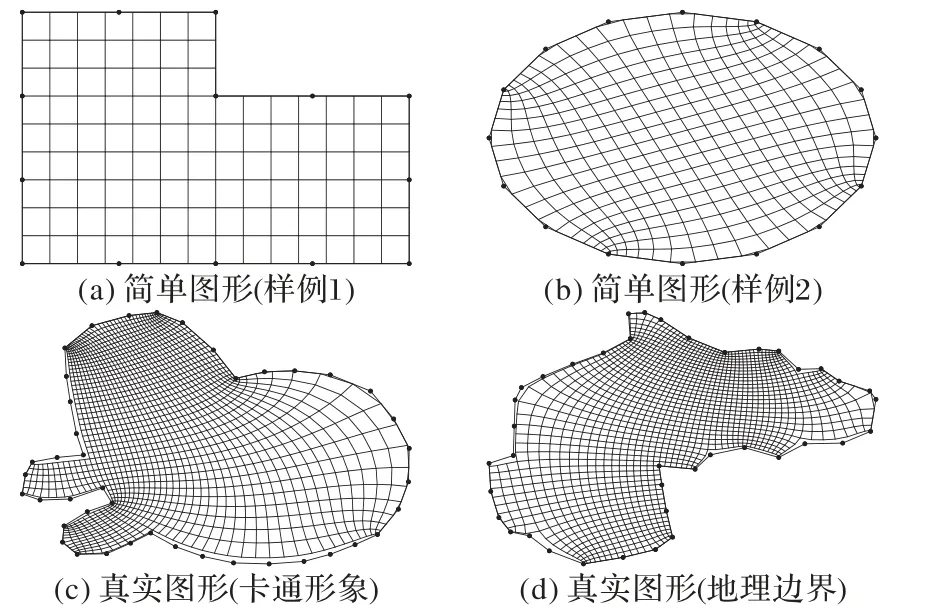
图7 正交网格生成样例Fig.7 Examples of orthogonal grid generation

接下来是考察真实目标区域，首先是如图7（c）所示的动画形象区域。在计算机图形学领域中，动画领域的模拟和计算应用是重要的课题。而图7（d）所示的是真实地理区域，以非洲大陆为例。在海洋科学和大气科学等领域，如天气预报、温度预测、模拟等问题上需要高质量的正交网格划分。与图7（a）和图7（b）相比，这两个样例所示的目标区域更为复杂，生成难度更大。从生成的正交网格结果来看，网格贴体性和正交性均保持较好水平，能满足科学计算的需求。

图8首先展示了图7（c）和图7（d）两种具有较复杂边界的图形在不同的L的取值下，最优化问题（5）的可行解的个数。另外图8中baseline 表示的是若没有使用本文算法的情况下，对于40-L边形公式（4）的可行解个数（图7（c）和图7（d）的目标多边形均为40边形）。根据1.5节的分析，本文的算法可以将时间复杂度从至少O(3N)降为大约至少O(2N-L)，从图8 可以看出，最优化问题（5）需要枚举的可行解个数已经大幅度减少，当L为31时分别减少了88.42%和91.16%的可行解数量，说明了算法的有效性。

正交网格是天气预报、气候模拟等科学应用中最为重要的网格。表1 展示的是这些领域中部分先进的正交网格生成工作。自动化网格生成是减少人力成本的关键，如图9所示。

在Linux16.04，CPU 为i7-8700 环境下对比SCtoolbox 和本文方法。注意到SCtoolbox［28］也是开源且自动化生成网格方法，对于图9（a）、（b）的 简单图形来说，本文方法与SCtoolbox 生成网格相同，但本文方法生成速度有明显优势。对于边界复杂的图9（c）、（d）而言：一方面SCtoolbox 在面对复杂边界的时候效果较弱，所示样例的网格点集中在图形底部，没能较好地进行网格划分；另一方面，SCtoolbox在复杂图形样例中同样需要更多的时间。Delft3D［30］是优秀的商业软件，在实际工程任务中被广泛使用，但其生成网格的过程中仍然需要一定的人工先验信息。注意到大多数工作都是由C/C++或者Matlab编写，而本文方法由Python实现，这使得本文方法具有很强的可扩展性，为科学计算领域提供更大的便利，特别是在人工智能科学计算的应用上。

3 未来的工作

3.1 更多的转角类型

实际上，基于Gridgen-c 工具的网格生成并不一定能保证得到很好的正交网格，即最优化问题（5）的最优解并不一定能满足科学计算的需要，其主要的原因在于Gridgen-c 工具本身，即它只有三种转角类型，分别刻画了180°、90°和270°的转角，然而这并不能对所有多边形都有效，如图10所示。

首先，右上、右下、左下三个转角应该选择90°（即转角类型1），而左上两个角有对称性，它们应该要有一样的转角类型，但是可以验证不管它们选择怎样的转角类型都不能满足式（4）。这说明利用Gridgen-c工具不能很好解决图10所示的区域的网格生成问题。再比如一个顶点数足够多的正多边形（接近圆周），其顶点的选择也是会面临一定的困难（图7（b））。这意味着应该考虑更多的转角类型，如针对图10 的样例，可以以45°为间隔的转角，即180°、135°、90°、45°、225°、270°以及315°这7 类转角，这样对于更加复杂的目标多边形能得到更加适合的转角方案。不过这样，一方面，图3 区域A中的正交网格划分将不再适用，需要更好的划分方式；另一方面，由于考虑了7 类转角，所以最优化问题（5）的时间复杂度至少为O(7N)，此时即使有图6 的策略仍然很难让时间复杂度降为可以承受的范围，所以，转角类型的设定需要有更多的研究和考虑，是未来工作的一个重点。

3.2 获得更好的分类器

分类器性能的好坏是本文提出算法的关键。根据图6 及其分析，如果能直接确定下来的转角类型较少，那么意味着并不能大幅度地降低计算量。同时，若被直接确定的转角类型由于分类器的性能较弱判断失误，那么对后续关于最优化问题（5）的求解会带来严重的干扰。为了获得更好的分类器，可以从3个角度来思考。

生成的算法 随着机器学习和深度学习领域的不断进步，对于序列类型数据的处理和相关分类问题的算法将越来越强，未来可以不断地将LSTM 替换成相应的算法来完善分类器的性能。

数据集的选择 在1.6 节中提到了本文算法使用的训练集数据为GADM 数据集，该数据集的优点在于数量大且多边形的边界形状更接近于自然区域，符合一定的物理规律。然而，由于地理类型数据边界形状的多样性，GADM 的数据集里仍然存在少部分形状比较独特的多边形，如3.1 节的分析，这类多边形关于最优化问题（5）往往没有较好的解。于是这类多边形数据在训练的时候便会引入较大的噪声，影响分类器的性能。在深度学习领域，有很多经典数据集，如ImageNet2012［21］、COCO［22］、CIFAR10/100［23］等，它们都经过较好的筛选和人工标记。而由1.6 节，本文所使用的数据集仅仅进行了适量的预处理，这使得数据集的质量并不能有足够好的保证。这意味着，网格生成领域也需要有高质量的标准数据集，而这需要较大的人力和物力。

增加训练集多边形的顶点数 由于最优化问题（5）时间复杂度的限制，在训练LSTM 的时候，采用的是N=10的多边形。然而仅仅使用顶点数为10 的多边形进行训练的话，不一定能满足超大规模多边形的网格生成需求。如图11 所示的是利用不同顶点数量多边形训练得到的分类器去处理图7（d）的结果，从结果来看，这说明了提升训练集多边形的顶点数对网格的生成有很大的帮助。另外，在求解最优化问题（5）的时候实际是遍历满足式（4）的所有解的组合，而这些解相互独立，非常适合采用分布式的计算，随着高性能计算领域的发展，利用多线程CPU 或者GPU 等方法能大幅度地加速式（4）的遍历，由此能得到顶点数足够高的多边形数据集，从而提升分类器处理更大规模网格生成问题的能力。

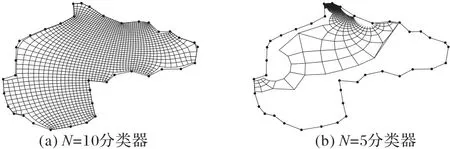
图11 训练集中多边形顶点数的影响Fig.11 Influence of polygon vertex number in training set

4 结语

本文首次对正交网格生成问题在数学上将SC 映射和整数规划问题建立联系，构建了一套较为完整的分析框架。由所提出的基本假设，利用循环神经网络LSTM 和目标多边形自身的信息，可以大幅度地减少网格生成所需计算量。由于对于平面上正交网格的生成问题可以归结为多边形区域的网格生成问题，本文所提出的方法具有一定通用性，实验表明，在简单图形区域，动画图形区域以及地理边界区域等多类型区域上均能自动化地产生高质量正交网格。