基于NTRU的多密钥同态加密方案解密结构
车小亮,周昊楠,周潭平,,李宁波,杨晓元,
(1.武警工程大学密码工程学院,西安 710086;2.网络与信息安全武警部队重点实验室,西安 710086)
(*通信作者电子邮箱smo_mrche@yeah.net)
0 引言
多密钥全同态加密(Multi-Key Fully Homomorphic Encryption,MKFHE)方案支持对不同用户的密文进行任意的同态运算,且运算之后的结果必须由参与计算的所有用户联合解密,可以较好地解决多用户密文进行同态计算的问题[1-2]。基于NTRU(Number Theory Research Unit)的多密钥全同态加密方案是基于多项式的加解密运算,密文和密钥量小,加解密结构简单,是公认的基于格的运算速度较快的加密方案之一,具有较强的实用性。
NTRU 型MKFHE 最初是由López-Alt 等[3]提出的,被称为LTV12(López-alt-Tromer-Vaikuntanathan)方案,其安全性基于2 的幂次多项式环上的LWE(Learning With Errors)问题[4]和DSPR(Decisional Small Polynomial Ratio)假设问题[3]。DSPR假设是非标准性假设,Stehlé 等[5]已经证明了在特定条件下DSPR 假设可以规约到RLWE(Ring Learning With Errors)困难问题。但2 的幂次分圆多项式环无法抵御子域攻击[6-7],且可选环较少,致使NTRU 型同态加密方案的安全基础受到了威胁。2017 年,Yu 等[8]提出基于素数次分圆多项式环上的NTRU 方案,该类环可有效应对子域攻击威胁,但参数选取较大;同年,Yu等[9]又相继提出了基于素数幂次分圆多项式环的NTRU 方案,该类环能有效抵御子域攻击的同时,使得密文密钥等参数尺寸与2 的幂次分圆多项式环上参数尺寸选取在同一量级,且可选环较多。本文研究NTRU 型多密钥加密方案的解密结构的安全基础即是基于素数幂次分圆多项式环上的困难问题。
另外,LTV12方案在进行解密运算时运算复杂度高,产生的噪声大,计算效率具有很大提升空间。主要是因为NTRU型多密钥加密方案的原始解密结构在进行一次同态运算时,需要频繁使用密钥交换技术[10],会使产生的噪声呈指数级增长。所以在实现全同态运算时,必须使用模交换技术[10]以控制噪声的增长。Doröz 等[11]通过优化参数提高了LTV12 方案的效率,但其同态解密结构没有改变;Bos 等[12]改进了NTRU方案的解密结构,使产生的噪声降低;陈智罡[13]和李子臣等[14]通过扩展密文向量改进了NTRU 方案的解密结构,消除了密钥交换过程,这些改进均是针对NTRU 型单密钥同态加密方案。对于NTRU 型多密钥同态加密方案,受参与用户数量影响,使得参数选取更加复杂,产生的噪声更大。为了提高NTRU型多密钥同态加密方案性能,本文研究了NTRU多密钥同态加密方案的解密结构,提出了两种优化改进的解密结构形式,并对三种解密结构的性能参数进行了对比分析。
1 相关知识
本文用λ表示安全参数,negl(λ)表示一个可忽略的函数。a表示向量,A表示矩阵,ai表示向量a中的第i个元素。v⋅表示向量v,w∈Rm的内积。对于向量的长度,一般用范数(Euclidean norm)度量。例如l1范数,定义为||v||1= |v1|+ |v2|+ …+ |vm|;无穷范数l∞定义为||v||∞= max{|v1|,|v2|,…,|vm|}。
高斯分布[15]对于任意的σ>0,定义Rn上的高斯函数为:∀x∈Rn,ρσ(x)= exp(-π||x||2/σ2);ψσ表示R上的高斯分布:ψσ=ρσ(x)/σ,x∈R;Rn上的球形高斯分布(spherical Gaussian distribution)表示为ψnσ,即对于(v1,v2,…,vn)∈Rn中的任意vi分别服从高斯分布ψσ。
正则嵌入下的离散高斯分布[9]设P(x)∈Z[x]是首一的n阶不可约多项式,。P(x)在复数域下的根为w1,w2,…,wn。正则变换矩阵为:(其中0 ≤i≤n- 1,1 ≤j≤n)。设t=tn-1xn-1+tn-2xn-2+…+t0∈R,系数嵌入表示为(tn-1,tn-2,…,t0),正则嵌入变换表示为σ(t)=(tn-1,tn-2,…,t0)V。正则嵌入下的离散高斯分布t←DZn,σ:σ(t) ←ψnσ,t=σ-1(t)=σ(t)⋅V-1,DZn,σ(x)=ρσ(x)/ρσ(Zn)。
素数幂次分圆多项式环[9]对于n=dν-1,d为素数,则Φn(X)=Φd(Xdν-1),则环R=Z[X]/Φn(X)和Rq=R/qR即为素数幂次分圆多项式环。因此在环Rq=R/qR上的加法和乘法运算是按系数逐个进行的,且系数取值区间为[-q/2,q/2)(q不等于2)。令χ是环R上的错误分布,设χ的界是B,则χ中多项式的系数均在[-B,B]区间,即a←χ,则。
下面给出素数次分圆多项式环上噪声增长特性,并讨论最坏情况下噪声增长的规律。
引理1[9]令n=dν-1,d为素数,其中Φn(X)=Φd(Xdν-1),环R=Z[X]/Φn(X),对于任意a,b∈R,最坏情况下,则有||ab||∞≤2φ(n)||a||∞||b||∞,这里φ(n)是关于参数n的变量。
由引理1容易得到如下推论。
推论1令χ是环R上的界为B的离散高斯分布,对于a,b∈χ,考虑最坏情况,则||ab||∞≤2φ(n)B2,特殊地,当b的界是1时,||ab||∞≤2φ(n)B。
推论2令n=dν-1,d为素数,环R=Z[X]/Φn(X),其中Φn(X)=Φd(Xdν-1)。χ是环R上的错误分布,设χ的界是B,λ是安全参数,模q是素数。令s1,s2,…,sk←χ,则:
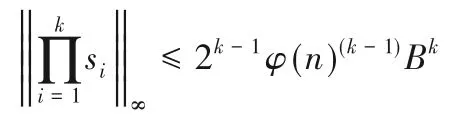
定义1RLWEΦ,q,d,χ问题(基于素数幂次分圆多项式环的LWE 问题):令n=dν-1,d为素数,Φn(X)=Φd(Xdν-1)。定义多项式环R=Z[X]/Φn(X)和Rq=R/qR,以及环R上的Bbound 截断(正则嵌入下的)离散高斯分布χ。RLWEΦ,q,d,χ假设是指区分以下两个分布是困难的:1)元组(ai,u)在上随机均匀分布的;2)随机均匀选取ai,,e←χ,输出的元组。
定义2DSPRΦ,q,d,χ假设(基于素数幂次分圆多项式环的DSPR 假设):令n=dν-1,d为素数,Φn(X)=Φd(Xdν-1)。定义多项式环R=Z[X]/Φn(X)和Rq=R/qR,以及环R上的Bbound截断(正则嵌入下的)离散高斯分布χ。DSPRΦ,q,d,χ问题是指难以区分以下两个分布:1)多项式h= 2g/f,其中f=2f'+ 1 且在Rq上可逆,f',g←χ;2)在Rq=R/qR上随机均匀采样得到的多项式u。
位展开技术[16]同态加密方案中经常用到BitDecomp(*)函数和Powersof2(*)函数进行比特位展开。令,这两个函数简述为:
BitD(x∈Rq):Rq→。 对于多项式x∈Rq,输 出x↦(x0,x1,…,xl-1)∈;
Pof2(y∈Rq):Rq↦。 对于多项式y∈Rq,输 出y↦(y,2y,…,2l-1y)。
对于多项式x,y∈Rq,容易验证:。
密钥转换技术(key-switching)[10]就是将密钥f转换成密钥fevk,将对应的密文由c∈Rq(对应解密密钥为f)转换成为想要的密文形式cevk∈Rq(对应解密密钥为fevk)。对本文来说,令。则:
1)Key SwitchGen(f∈R,fevk∈Rq):给定h∈Rq,sτ,eτ←χl。输出计算密钥:
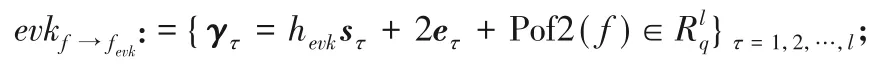
2)Key Switch(c,γτ,q):计算,输出:cevk=。
2 基于NTRU 的多密钥同态加密方案的解密结构研究设计
基于素数幂次分圆多项式环上的LWE 问题和DSPR 假设,可有效抵御子域攻击。本文对NTRU 型多密钥同态加密方案的解密结构研究与分析基于素数幂次分圆多项式环上。本章首先给出了基于素数幂次分圆多项式环上的NTRU 多密钥同态加密方案模型,研究分析其原始的解密结构特性,而后改进设计了两种解密结构,最后对其性能及参数进行对比分析。
2.1 素数幂次分圆多项式环上的NTRU 多密钥同态加密方案
令n=dν-1,d为素数,Φn(X)=Φd(Xdν-1),多项式环R=Z(x)/Φn(X)和Rq=R/qR。设在R上的错误分布χ的界为B=B(λ),则错误分布空间的界亦为B。令K1,K2为两个N个用户的公钥集合,不失一般性,设K1∩K2=,K1∪K2={pk1,pk2, …,pkr}, 这 里j∈[0,N],r∈[N,2N]。基于素数幂次分圆多项式环上的NTRU型多密钥同态加密方案描述如下。

根据LTV12 方案[3]的分析可知,加法同态运算产生的噪声远小于乘法同态运算,所以只要乘法同态运算满足全同态运算,则方案是全同态方案。此原始方案的同态乘法解密结构的性能直接影响设计方案的效率问题。下面详细分析该方案中的解密结构性能及参数,并讨论影响方案效率的因素。
2.2 NTRU多密钥同态加密原始解密结构
2.2.1 设定条件
对于t∈[1,j],联合解密私钥为Ft=Ft-1(ft)-1,其中F0=。
2.2.2 解密结构
利用联合解密私钥解密时,要先进行密钥交换将密文乘积线性化,经过一次密钥交换后可得:
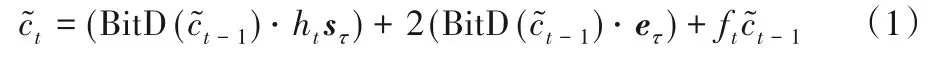
由式(1)可知,经过j次密钥交换循环,可得
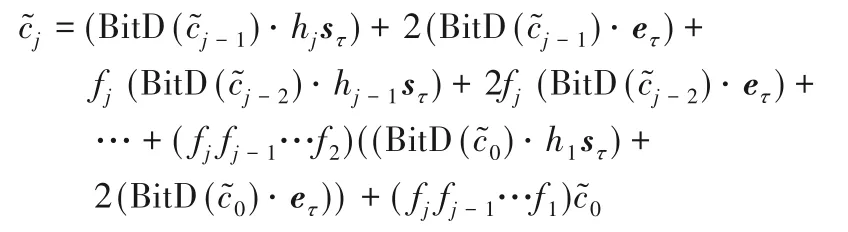
利用联合解密私钥Fj进行解密,可得:
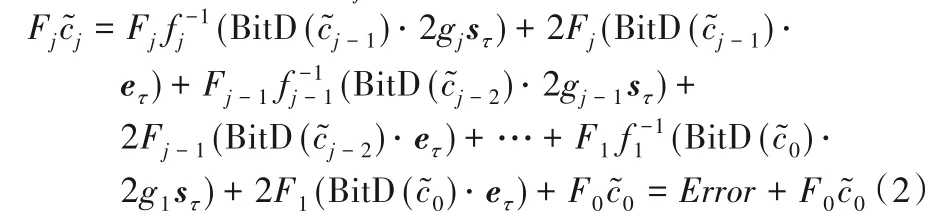
式(2)即为LTV12的原始解密结构形式,完成正确解密的条件是式(2)中Error是2的倍数,且。由式(2)可以看出,密钥交换的作用是线性化密文乘积,形式上是建立了与的等式关系,本质上还是利用NTRU 型同态加密方案最初的解密结构形式。 设,则可得:
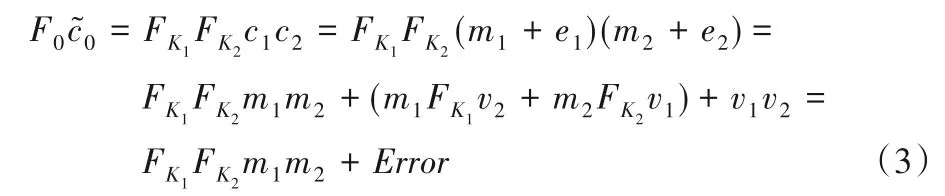
2.2.3 噪声分析
设联合解密产生的噪声参数为δ,一个新鲜密文解密产生的噪声参数为δ0。对于,设||ciFKi||∞≤δ。假设最坏情况下得到联合密文ci,即ci是集合Ki中N个用户的新鲜密文的乘积。设一个新鲜密文解密产生的噪声为,根据引理1 和推论1,容易得到δ0=(2B+ 1)+ 3φ(n)(2B+ 1)2,所以根据推论2可得δ≤2N-1φ(n)N-1(δ0)N,为了方便计算,令EN≤2N-1φ(n)N-1(2B+1)N。
由式(2)可以得到原始解密结构产生的解密噪声为:
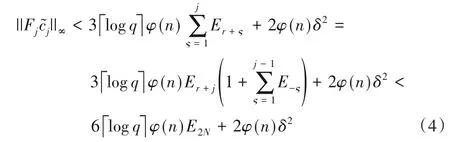
所以由式(4)进一步可知,产生的噪声为:
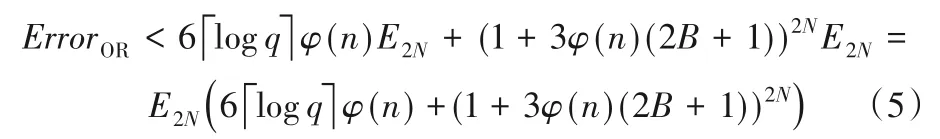
取式(5)中的系数最大项,则此结构产生的噪声量级为Θ(32NE4N)。
2.2.4 性能及参数分析
式(3)称为NTRU 型同态方案的解密结构。受限于这种解密结构,同态乘法解密时需要用密钥交换技术来将密文乘积的重复部分线性化,最终约减为如式(2)的样式。其实是用计算密钥替换了重复的联合解密私钥部分,这样会导致噪声增长较快。由式(4)可知由密钥交换而产生的噪声增大了。
①安全性:该结构是基于素数幂次分圆多项式环上设计的,可有效抵抗子域攻击,其安全性基于RLWEΦ,q,d,χ问题和DSPRΦ,q,d,χ假设。
②参数选取:该结构的密文是2 个次数小于dν-1的多项式,其尺寸最大为2φ(n)logq;加密使用的公钥是2N个次数小于dν-1的多项式,所以公钥尺寸为2Nφ(n)logq;解密时用到r个次数小于dν-1的且系数小于(2B+ 1)多项式私钥,故其私钥尺寸大小为rφ(n)log(2B+ 1);每进行一次同态运算,要进行j次密钥交换,所以使用的计算密钥的尺寸为。由文献[11]知,素数幂次分圆多项式环与2的幂次分圆多项式环上的参数选取在同一量级,所以该解密结构参数尺寸与原始解密结构中参数尺寸的选取在同一量级。
③同态解密运算时间:为了方便运算效率的评比,文章模拟了实验消耗时间。忽略多项式不同系数([-q/2,q/2)内的实数)乘法耗时的差异性,定义两多项式完成一次乘法运算用时为Tmult,BitDecomp(*)函数进行一次多项式分解用时为TBD,完成个多项式求和运算用时为TA。以完成一次同态乘法解密为例,在不做任何模q和模2 处理的情况下,原始解密结构完成解密运算用时为:
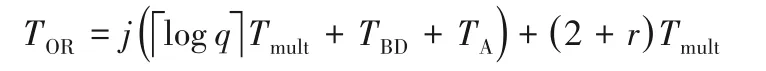
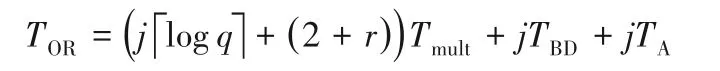
即Tmult前的系数为多项式运算次数,TBD前的系数为进行BitDecomp(*)分解次数,TA前的系数为多项式求和次数。
2.3 改进的NTRU型多密钥同态加密方案的解密结构
根据2.2节分析可知,影响NTRU型多密钥同态加密方案效率主要有两个方面:一是受原始同态乘法解密结构的限制和参与运算的用户数量影响,使得方案产生的噪声较大;二是受密钥交换次数j的影响,使得运算复杂性增大,运算时间较大。目前还没有很好的办法消除多密钥同态方案中用户N对产生噪声的影响,但可以通过改进NTRU 型多密钥同态加密方案中原始的解密结构,降低噪声,减少或消除密钥交换次数,以提高方案效率。
2.3.1 “Regev-Style”解密结构
文献[12]中对NTRU 型单密钥同态加密方案的解密结构进行了改进,即采用“Regev-Style”加解密模式[17-18],降低多项式的系数,减小噪声的产生。本节将此方法进行改进,并应用到多密钥同态加密方案中。
1)设定条件。
对于明文m∈{0,1},加密可得,对于联合密文c,解密形式为:(2/q)FKc=m+Error,即得m=;计算密钥为:;对于给定的两个多项式联合密文c1和c2对应的加密公钥集合分别为K1,K2。令。
2)解密结构。
同态解密时,同样需要循环进行密钥交换,即同式(2),可得:
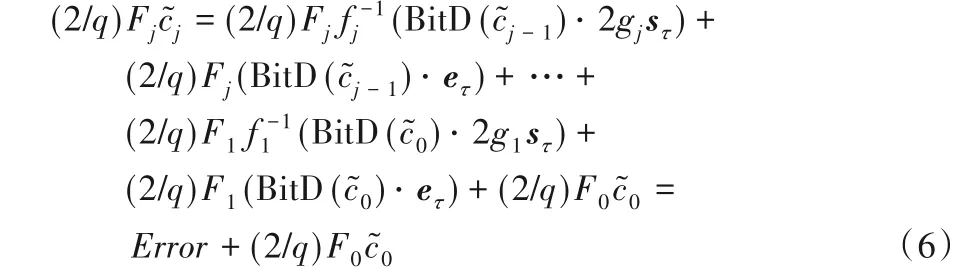
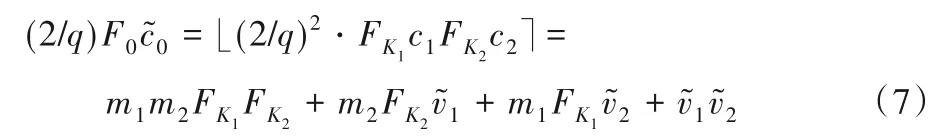
如式(7)所示,“Regev-Style”解密结构改变了初始解密结构的形式,运算,即可以恢复明文。
3)噪声分析。
设此情况联合解密产生的噪声参数为β,一个新鲜密文解密产生的噪声参数为β0。对联合密文c1和c2,令||(2/q)ciFKi||∞≤β,则最坏情况下,可得新鲜密文解密产生的噪声为β0≤(2B+ 1)+(4φ(n)/q)(2B+ 1)2,同原始解密结构,可得一个联合密文解密后产生的噪声为:
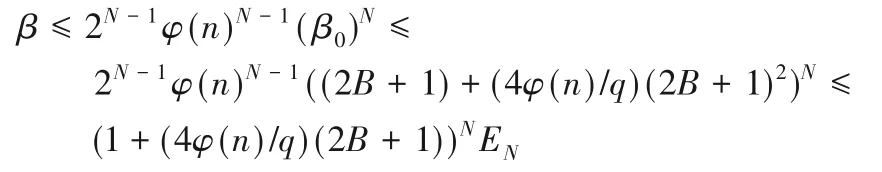
所以根据式(6)可得“Regev-Style”解密结构产生的噪声为:
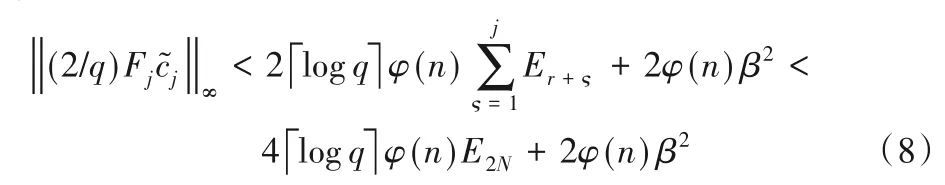
由式(8)进一步可得,产生的噪声为:
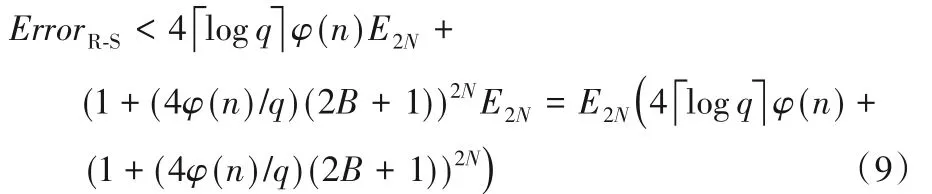
由式(9)知,参数q≫B,q≫φ(n),当受用户数量N影响较大时,可得(1+(4φ(n)/q)(2B+ 1))2N≤22N,则“Regev-Style”解密结构产生的噪声的量级为Θ(22NE2N)。
4)性能及参数分析。
“Regev-Style”解密结构在解密时要降低多项式系数,噪声较原始解密结构呈指数级降低。缺点是:仍没有消除密钥交换过程,且每进行一次解密运算,均要进行多项式系数的降低处理,使得运算复杂度增大。但由于每次的多项式降系数处理,大幅度降低了噪声,用于设计全同态方案时,可以减少密钥交换和模交换的使用次数,以提高效率。
①安全性。“Regev-Style”解密结构亦是基于素数幂次分圆多项式环上设计的,其可有效抵御子域攻击。另外,“Regev-Style”解密结构应用于NTRU 型单密钥同态加密方案中时,由于多项式系数较小,选取的参数满足SS11[6]中对于DSPR 假设规约到RLWE 的条件,因此其安全性只基于RLWE问题。而应用于素数幂次多项式环上的多密钥同态加密方案中,受用户数量N的影响,使得DSPR 假设到RLWE 问题的规约条件不适用于多密钥同态加密方案中。但在RLWEΦ,q,d,χ问题和DSPRΦ,q,d,χ假设成立条件下,“Regev-Style”解密结构是安全的,且能抵御更多的子域攻击。
②参数选取。“Regev-Style”解密结构加密时先增大明文的系数,即增大了多项式密文中的常系数,密文仍是2 个次数小于dν-1的多项式,其尺寸最大为2φ(n)logq,同样使用到的公钥、解密私钥和计算密钥尺寸与原始方案相同。
③同态解密运算时间。“Regev-Style”解密结构在完成一次密文与密钥相乘后,均要进行多项式系数的降低处理,设对多项式降系数处理用时为Δt。其他运算消耗的时间设定与原始解密结构相同,则“Regev-Style”解密结构完成一次同态解密用时为:
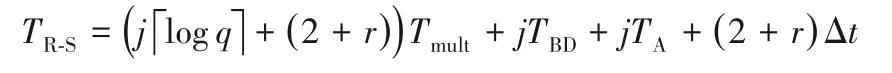
相对于原始解密结构,由于每次解密均要做多项式降系数处理,所以运算时间增加了(2+r)Δt。
2.3.2 “Ciphertext-Expansion”解密结构
文献[13-14]通过扩展密文向量完成对解密结构的改进,本节对其设定条件进行改进,并应用到NTRU 型多密钥同态加密方案中,可消除NTRU 型多密钥同态加密方案中的密钥交换过程。
1)设定条件。
2)解密结构。
对于给定的两个联合多项式密文向量c1和c2对应的公钥集合分别为K1,K2,令K=K1⋃K2。
同态解密时,先进行密文变换,可得:
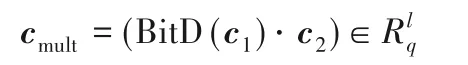
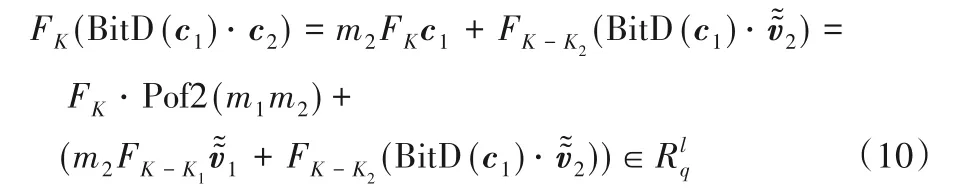
取式(10)的第一项进行(mod 2) 运算,可得m1m2=。当时,完成正确解密。
3)噪声分析。
设此情况联合解密产生的噪声参数为η,一个新鲜密文解密产生的噪声参数为η0。对联合多项式密文向量ci,有。易得新鲜多项式密文向量解密时产生的噪声中η0≤3φ(n)(2B+1)2,同理原始解密结构,最坏情况下,可得一个联合多项式密文向量解密后产生的噪声为:
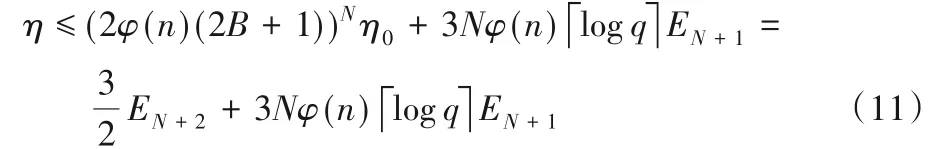
由式(10)可得,“Ciphertext-Expansion”解密结构产生的噪声为:
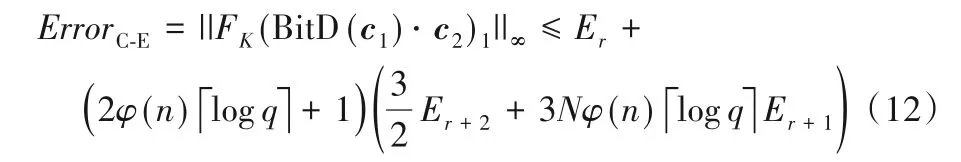
4)性能及参数分析。
“Ciphertext-Expansion”解密结构通过密文扩展,使加解密在多项式向量下完成运算。该方法消除了密钥交换过程,使得产生的噪声较小,缺点是密文空间增大了。
①安全性。“Ciphertext-Expansion”解密结构是用Powersof2(*)将密文变换为向量形式,计算过程使用BitDecomp(*)函数进行多项式向量的转换。根据文献[3,16]可知,函数BitDecomp(*)和Powersof2(*)对安全性没有影响。所以“Ciphertext-Expansion”解密结构的安全性与原始解密结构和“Regev-Style”解密结构相同,安全性是基于RLWEΦ,q,d,χ问题和DSPRΦ,q,d,χ假设,可抵御更多的子域攻击。
③同态解密运算时间。假设运算消耗的时间设定与原始解密结构相同。由于“Ciphertext-Expansion”解密结构输入的是两个维的多项式密文向量,解密时只取密文向量的第一项进行求和运算。所以完成一次同态解密运算用时为:
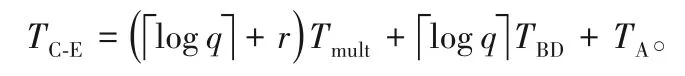
与原始解密结构运算时间进行差运算:
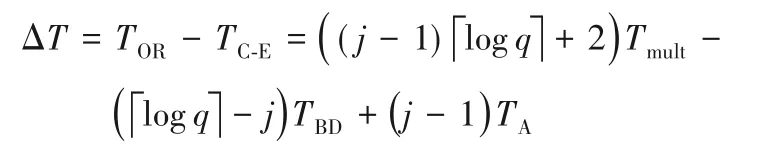
参数Tmult、TBD和TA的大小关系受参数q和n的影响,通过选取合适参数的j,q和n,可使ΔT>0。
2.4 解密结构性能参数对比分析
综合分析上述三种解密结构,以完成一次同态乘法运算为例,给出原始解密结构、“Regev-Style”解密结构和“Ciphertext-Expansion”解密结构性能及所有参数尺寸对比,具体如表1、2。
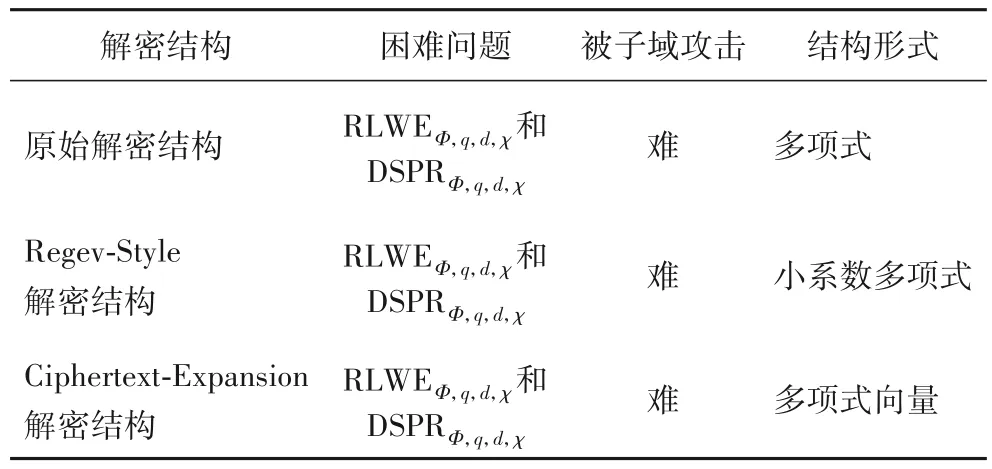
表1 3种解密结构的性能对比Tab.1 Performance comparison of three decryption structures
如表2 所示,与原始解密结构相比,“Regev-Style”解密结构产生的噪声呈指数级降低,但由于每次解密运算要进行多项式降系数处理,使得运算时间增大。同样与原始解密结构相比,“Ciphertext-Expansion”解密结构产生的噪声呈指数级降低,且当两个公钥集合K1、K2的交集个数j越大,噪声值就越小;另外,“Ciphertext-Expansion”解密结构无需进行密钥交换,虽然密文尺寸增加了,但设计全同态方案时,可以通过选取合适的参数,使ΔT>0,减少运算时间,提高效率。

表2 3种解密结构的参数对比Tab.2 Parameters comparison of three decryption structures
3 结语
NTRU 型多密钥同态加密方案的解密结构影响方案的效率,本文对原始的多密钥同态解密结构进行了分析,优化改进了两种多密钥解密结构,并对其参数性能进行了分析,为设计NTRU 型MKFHE 方案提供了解密结构基础。通过分析,“Regev-Style”解密结构产生的噪声较小,虽然运算复杂度增大了,但应用于多密钥全同态加密方案中,通过控制多项式系数,可以减少密钥交换和模交换的使用次数。“Ciphertext-Expansion”解密结构无需使用密钥交换技术,产生的噪声较小,适用于设计参与计算的用户重复较多的全同态加密方案,并可通过控制参数选取以提高方案运算效率。

