高等数学课程实践教学课题的研究设计
李 华
(西安航空学院 理学院,西安 710077)
0 引言
高等数学作为高校理工类本科教学的基础课程,其理论和实践方面的教学改革颇受关注。高等数学课程传统的教学方式是“灌输式”,学生模仿解题思路做题但缺乏创新性的解题方法,数学知识的本源和应用被掩盖。近几年,随着高校教育教学改革的不断深化,案例式教学、问题驱动式教学、MOOC、翻转课堂等新的教学模式相继出现,改革的目标是从以“教”为主向以“学”为主转变,激发学生学习的内驱力以及自主学习的能力,培养学生的实践创新能力。熊文俊[1]采用了问题驱动式教学模式,有效调动了学生积极性,让学生更好的参与到教学过程中,是一种探究式教学。夏红[2]等人借助MOOC对微积分的教学模式进行探究,采用复合式教学,将网络教学模式与课堂相结合。张卫国[3]等人采用带有对问题探讨因素的启发式教学,并结合数学实验、数学软件和数学建模课程,构建了培养学生创新能力的课程体系。
李大潜教授指出,数学上的不少概念、方法或理论,有些本身就来自其在现实生活中的原型[4]。数学实验教学存在一些问题,如实验素材拘泥于教材,与学生的具体专业、研究问题和生活不够紧密[5]。基于此,本文在选取实践课题时,一方面遵循课本,是对课本的概念、定理、方法的验证和具体操作;一方面选取学生感兴趣的生活实例,是对高等数学课程的具体应用,能够使学生直观感受微积分的概念和应用方法。
1 实践课题的设计思路与方法
高等数学课程实践课题的设计是根据高等数学课程的知识体系,遵循微积分教学四原则(图像、数值、代数、自然语言)来设计小课题和实验,使学生对高等数学的定义定理有直观深入的理解,并了解其简单的应用。
课题按照不同的实验目的分为验证型、应用型和探索型实验[6],实验预先明确实验目的、对应的知识点和使用的程序。对于验证型实验,设置在相应章节讲授之前完成,要求学生有目的地预习,并了解知识的背景和应用。对于应用型实验,设置在章节内容讲授之后,是对本章知识的凝练和提取,具有较强的综合性,且是学生熟识或感兴趣的问题,是对所学知识的使用和实现。对于探索型实验,题目设置较灵活,可由学生自己寻找和设计,注重实验实施的过程和方法,不以实验结果为唯一的考查目标。
2 课题的分类和示例
2.1 验证型课题
对高等数学中抽象的定义定理,通过数值计算及绘制图形的方式,使其具体化、形象化,让学生了解其来源和应用,并对数学有直观的认识。
实验例1[7],利用麦克劳林公式,用幂函数近似表示指数函数ex,ex的麦克劳林公式:
取n=1,2,3,4,5
n=1ex≈1+x
幂函数近似指数函数的图形见图1所示。从图形上看,随着次数n的增大,一方面幂函数的表达式越发复杂,一方面幂函数越逼近于ex,在实际应用中,n需要适当选择。从图1显示的幂函数次数的变化过程,可以使学生直观地感受麦克劳林公式的作用,体会用幂函数近似指数函数表示复杂函数的过程,体会微积分中“近似”的思想。

图1 幂函数近似指数函数的图形
实验例2[7],傅里叶级数近似矩形波。将矩形波的波形函数展开成傅里叶级数,选取不同阶数的部分和函数并绘制其图像,揭示傅里叶级数近似矩阵波的过程,使傅里叶级数的产生背景和应用实例具体化,使傅里叶级数的概念更加直观清晰。矩形波的傅里叶级数展开式:
用MATLAB分别绘出傅里叶级数前1,2,3,5项部分和的图形,并与矩形波图形作比较。如图2所示。
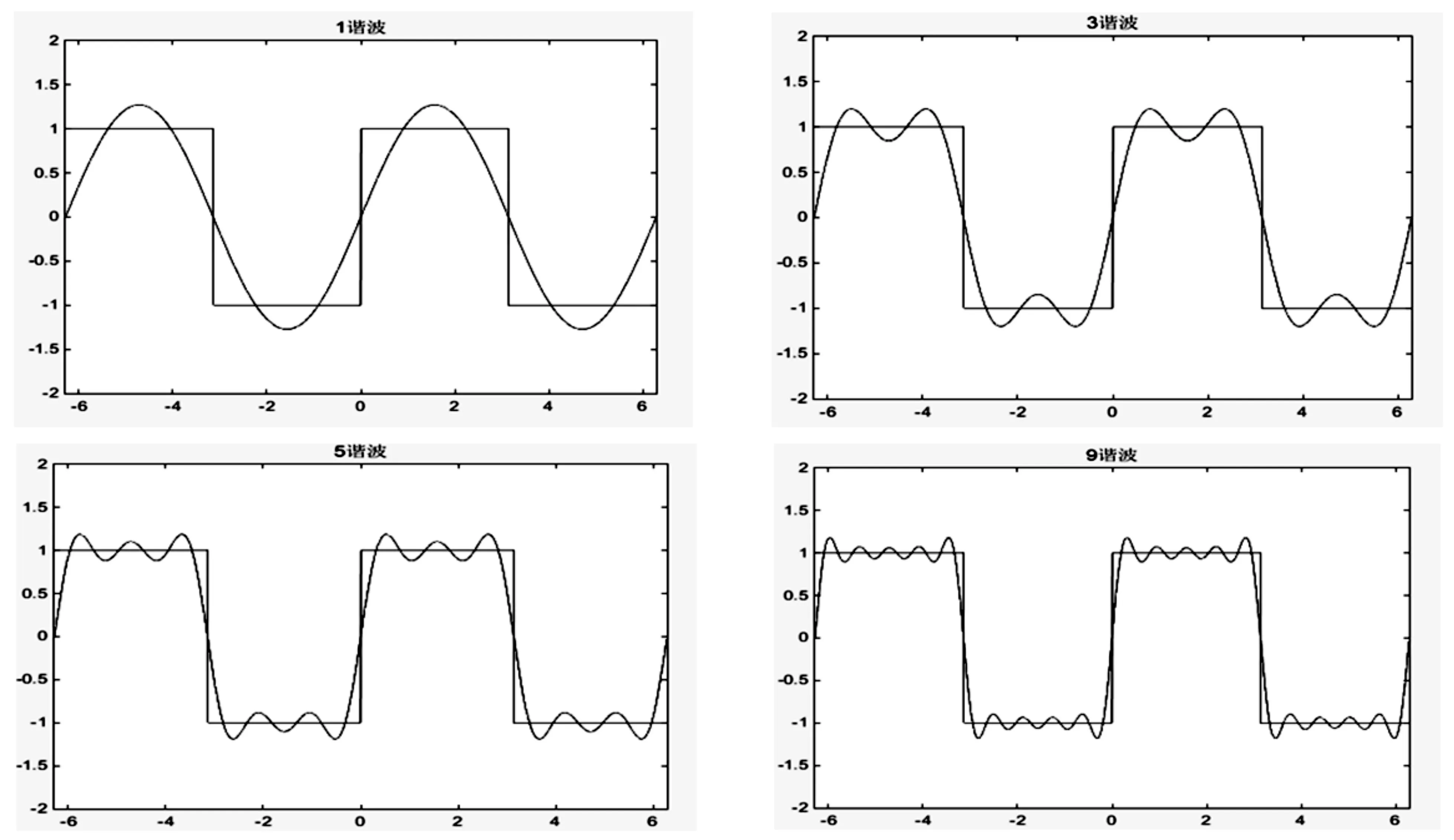
图2 傅里叶级数前1,2,3,5项部分和的图形
从图2可知,矩形波是由一系列不同频率的正弦波叠加而成的。通过实验,让学生理解傅里叶级数的作用和级数产生的背景,进一步探究级数在本专业和现实中的应用。
2.2 应用型课题
选取学生熟识的且与生活息息相关的问题作为小课题,该课题是高等数学课程的运用的过程,能将所涉及知识的应用背景及本质呈现出来。
实验例3,选取碗作为实物并计算其体积和表面积。建立空间直角系,在坐标系下测量相关数据,建立曲面方程,运用三重积分计算体积,运用第一类曲面积分计算表面积,如图3所示。该课题在完成过程中,需将多个知识点连接起来,具有较强的综合性,达到应用知识和解决问题的目的。
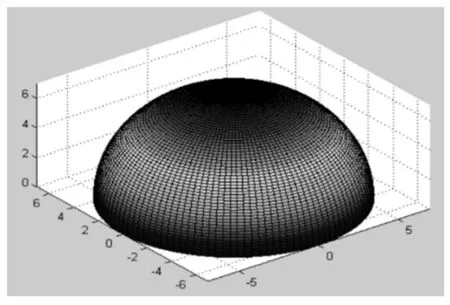
图3 碗的旋转抛物面
建立空间直角坐标系,建立旋转抛物面的方程
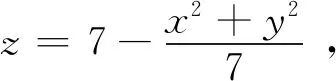
利用第一类曲面积分求表面积:
计算结果:碗的体积约为538.78cm3,表面积约为344.2195cm2。
实验例4,计算一片品客薯片面积的大小。该薯片具有不易破碎的特点,究其原因是其形状为双曲抛物面,即马鞍面,如图4、图5所示。
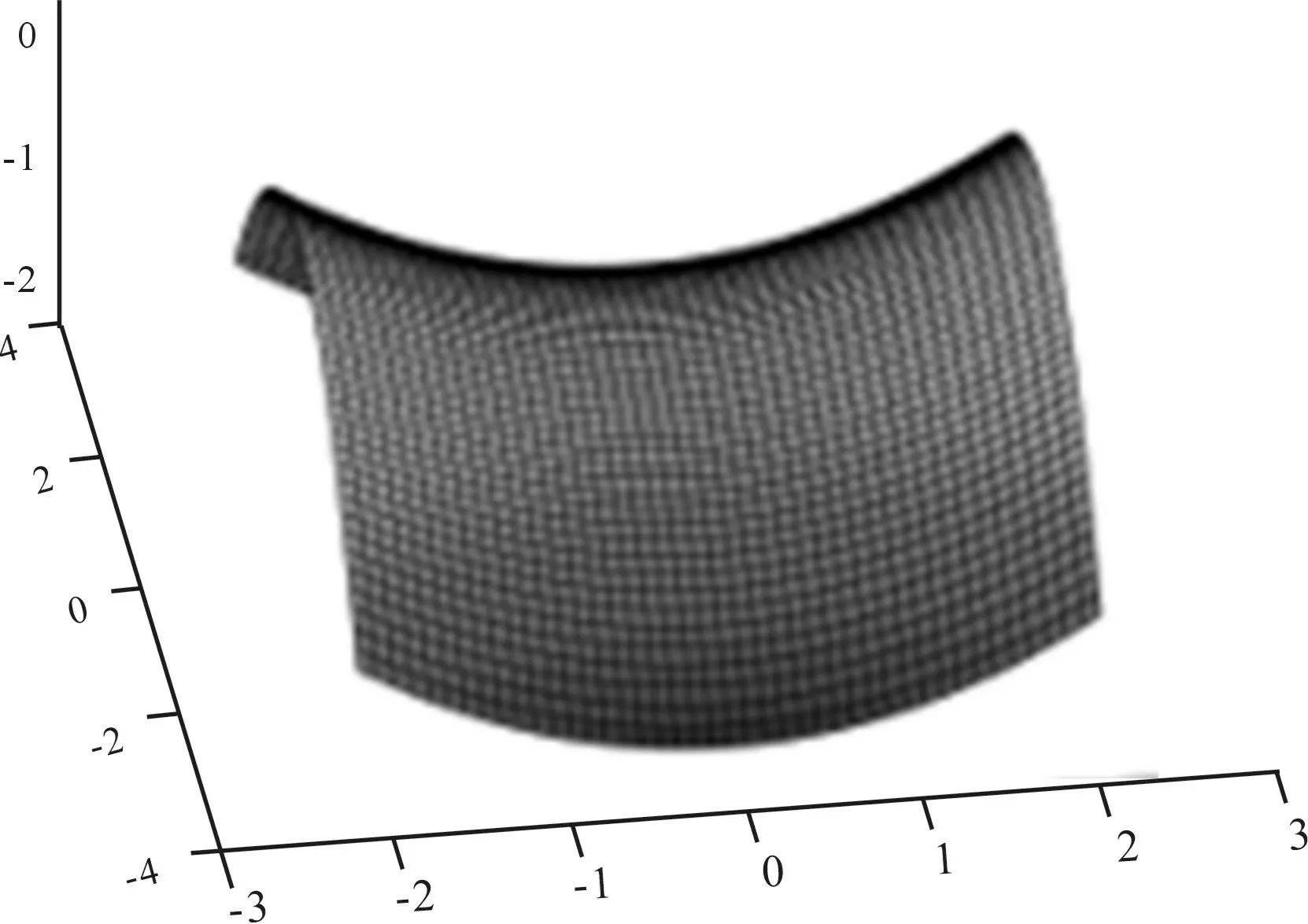
图4 马鞍面
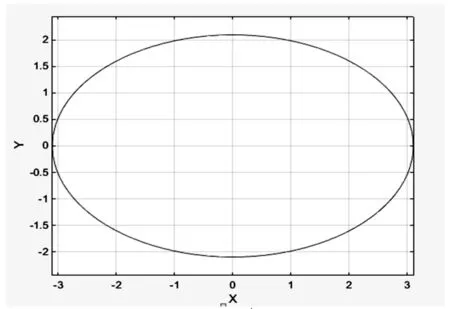
图5 马鞍面在XOY上的投影区域
建立马鞍面的方程为:
利用第一类曲面积分求表面积:
投影区域面积为:
S=20.452cm2
计算结果:一片品客薯片的面积约为48.256cm2,该曲面的面积约为其投影区域平面的面积的2倍。
课题设计过程中,当计算或画图难度较高时,可以给出相关程序代码,数学软件在小课题中只作为工具和辅助手段,不作为实验的考查点和目的。
通过实验,建立了空间直角坐标系及空间曲面方程,并将重积分和曲面积分的计算应用到曲面方程中。通过实例,将多元积分学的知识贯穿起来,具有较强的综合性和应用型,使重积分的背景和应用具体化,起到了“边学边用”的作用。
3 探索型实验
根据学生常见且关心的问题来设计实验,让学生能够应用高等数学知识,探索性地发现问题、解决问题。
实验例5,等额本金和等额本息两种还款方式。通过比较两种还款方式的月还款额,探究两种还款方式的优劣和试用的人群。
设贷款金额为m元,贷款年限为n年(共计12n月),年利率为x,每月归还利息为at元。
(1)等额本金与等额本息的月还款额:
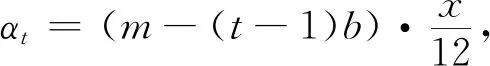
第t个月的还款额为b+αt,
(2)等额本金与等额利息前六个月每月利息的比较,设m=100000元,n=5年,年利率为6 %,如表1、表2所示。

表1 等额本金

表2 等额本息
(3)等额本金与等额本息的前五年月还款额的比较,如图6所示。
等额本息月还款额为 1933.28元。
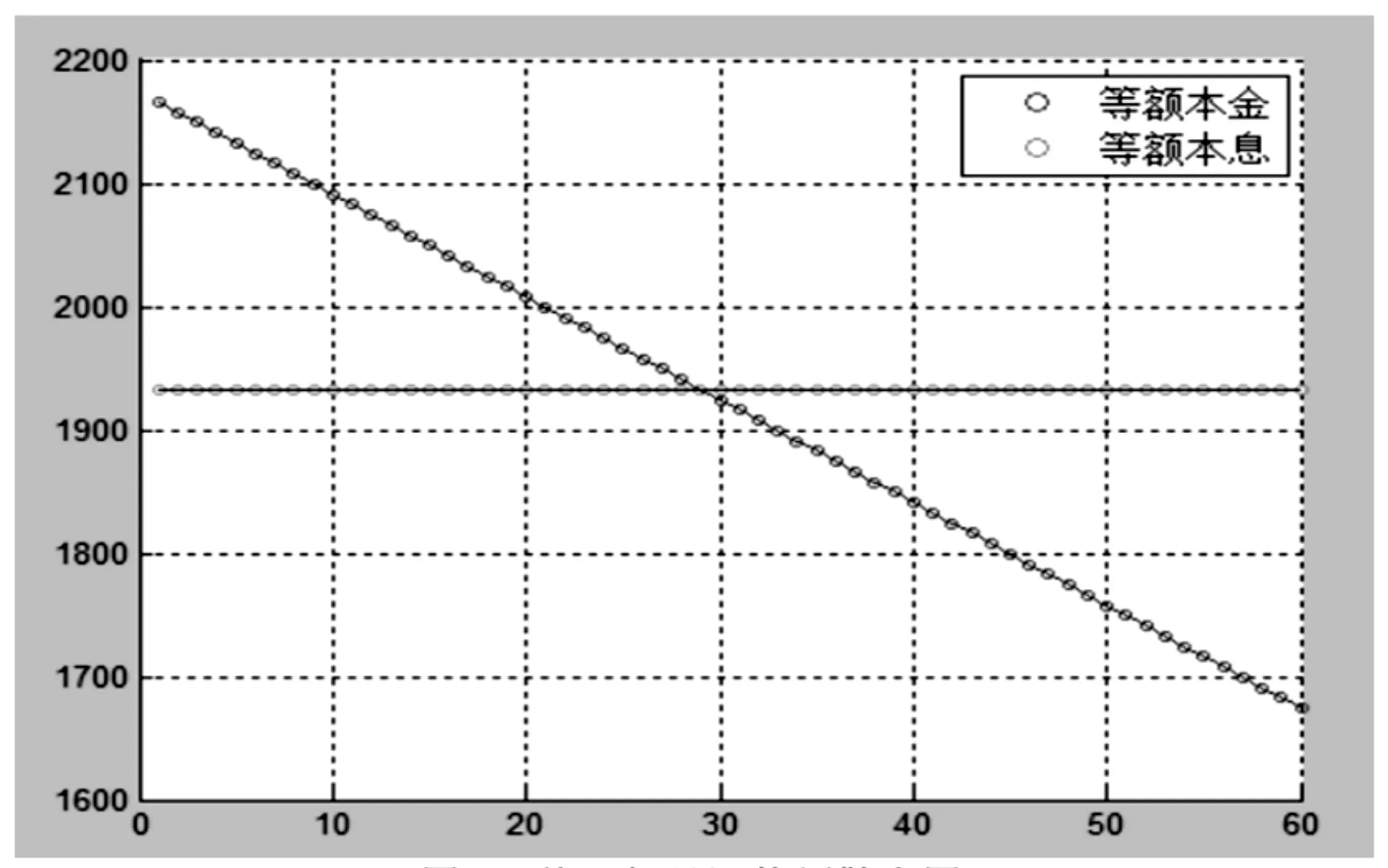
图6 前五年月还款额散点图
(4)实验小结
等额本金还款方式为月还款额,并且随着月份的增加而增长。前半段时期利息较高,每月还款额相对较多;后半段时期利息逐月减少,还款额越来越少,适合有一定经济能力的贷款人。约在第28个月时,等额本金和等额本息的月还款额相等。
4 结语
近几年出现了多种新型教学形式,如混合式教学、翻转课堂、MOCC、在线教育[8]等,其目的就是改革传统的教学模式,从以老师“教”为主体向以学生“学”为主体转变。本文研究了高等数学课程实践课题的设计,将小课题和实验穿插在教学过程中,或作为学生预习的导入,或作为学生知识的总结与提炼,让“学生边学边用”。通过对小课题的分析研究,让学生对高等数学的概念、定理有直观的感性认识。通过“用”数学,使学生对数学的思维和学习方法有更深入的理解,点燃其数学思维的火花[9],培养和提高学生分析问题、探究问题、解决问题的能力。