Zn-RG体系van der Waals势的理论研究
魏丽敏,段文瑞
(1.西安航空学院 理学院,西安 710077;2.陕西省计量科学研究院 光学计量测试中心,西安 710065)
0 引言
原子以及分子间的相互作用势对了解气体、流体和固体的动态和静态性质至关重要,是原子分子物理、物理化学和微观反应动力学等学科中的一个重要研究课题[1]。在分子势函数的研究中,原子位置是物质结构的表征基础,一方面可以对整个空间范围内分子性质进行完全的描述,同时也是研究分子振转运动、碰撞动力学的基础。对双原子分子势函数的研究由来已久,但精确的双原子分子势能函数至今仍为许多领域所需要。例如,在电子和双原子分子振动激发散射研究中,如果没有精确的双原子分子势能函数,就得不到分子精确的振动能级和振动波函数,也就无法求得精确的散射截面[2]。
由两个满壳层原子(第IIA族、第IIB族和第零族原子)构成的双原子体系,原子间由于瞬时偶极矩相互耦合而形成一个弱相互作用van der Waals键,组成分子的两个原子基本上保持了原来的电子结构,它们基态的结合能很弱。从理论上解薛定谔方程求如此微弱的van der Waals势时,要采用较大规模的基组,其中包括大量的极化函数,不仅耗时而且由两个大物理量相减来算得如此弱的结合能会造成较大的误差。从实验上获得van der Waals势,需要用到反演技术,比如RKR反演技术,但是在远离平衡间距的渐进区域,RKR结果的可靠性降低,在RKR方法基础上发展的IPA逆向微扰法也存在这个缺点。因此,很有必要寻求相对简单而又可靠的势模型对这类分子体系基态的van der Waals势进行研究。
关于双原子分子势能函数的表示形式,可以追溯到1920年由Kratzer A提出的Kratzer势,之后研究者们又发展了多种势函数模型[3]。1984年,Tang K T和Toennies J P教授从原子间相互作用的物理本质出发,在充分考虑了双原子体系的电子交换作用、库仑排斥作用、长程色散以及电子云重叠效应等因素后,提出了著名的Tang-Toennies势模型(TT势模型)[4]。TT势已成功地用于计算很多双原子体系基态准确的相互作用势[5-9],是本文计算的基础函数。
关于第IIB族和第零族的混合双原子分子Zn-RG (RG=He、Ne、Ar、Kr、Xe)体系基态van der Waals势的研究,已发表的各理论和实验结果之间差距较大[10-15]。一方面说明对结合能如此弱的van der Waals分子研究无论是理论计算还是实验测量都存在很大的困难,另一方面也体现出本文用组合规则从同核分子势函数得出异核分子势函数方法的优势。本文将应用TT势模型和势参数的组合规则计算得到Zn-RG系统各分子基态的van der Waals势,并给出各分子的光谱参数,对本课题组所研究的满壳层原子双原子分子van der Waals势进行必要的补充。
1 计算方法
1.1 Tang-Toennies势函数与约化势
1984年,Tang和Toennies教授提出了著名的描述van der Waals双原子分子势函数的Tang-Toennies势模型[4]:
其中,A、b为Born-Mayer排斥势参数,C2n为色散系数,其中C6表示偶极-偶极相互作用即色散能的主导项,C8表示偶极-四极相互作用,C10表示偶极-八极相互作用与四极-四极相互作用之和,nmax一般情况下取nmax=5就足够,更高阶项对势能的影响很小。这样,TT势仅需五个参数A、b、C6、C8、C10就可以描述分子全程区域的势能曲线。该模型不仅可以准确地描述原子间和分子间的相互作用势,还可推广用于描述原子与离子XY+间的相互作用势[16]。
为了方便下面分子光谱参数的计算,我们需要将TT势写为它的约化形式,称之为TT约化势,令:
x=R/Re(2)
U(x)=V(Rex)/De(3)
其中,Re为平衡间距,De为势阱深度,则TT势函数的约化形式为:
1.2 Tang-Toennies势参数的组合规则
对于短程区域的排斥势参数A和b,有几种合理准确的组合规则,能够给出相近的结果。本文将使用Böhm-Ahlrichs规则[17]用于排斥势参数A和b的计算,它们由假设的与能量相关的核心模型得出:
其中,R(V)表示在给定势能V时的核间距,单下标表示同核双原子分子的势参数,双下标表示对应异核双原子分子的势参数。此假设能够得出以下的组合规则:
Aij=[Ai1/biAj1/bj]bij/2(6)
对于长程区域的色散系数C6、C8和C10,本文使用的组合规则详见文献[18]的2.3小节,计算结果列于表1中。
1.3 Tang-Toennies势函数与光谱参数间的关系
在实验中,常用振动和转动光谱参数来表征势能的形状。将能量(v+1/2)k按和[J(J+1)]l幂级数展开:
其中,v和J分别是振动量子数和转动量子数,Ykl是Dunham系数[19],其中ωe表示振动频率,Be为转动常数,ωeχe为非谐性常数,αe为振动-转动耦合常数。将约化势函数在Re处关于x幂级数展开,可求得相应的光谱参数,约化势U(x)展开式为:
U(x)=-1+a0(x-1)2(1+a1(x-1)+a2(x-1)2+…) (9)
其中:
可用展开系数an表示如下三个无量纲的物理量[19]:
TT约化势是一个解析式,它的各阶导数可以直接得到,由它的导数值通过(10)式可以得到约化势级数展开系数a0、a1、a2。与平衡间距Re、势阱深度De,根据(11)-(13)式便可得到光谱参数ωe、ωeχe和αe的值。
2 计算结果与分析
表1列出了由组合规则(6)和(7)式计算得到的异核双原子分子Zn-RG势参数A和b的结果,稀有气体同核双原子分子He2、Ne2、Ar2、Kr2、Xe2以及同核双原子分子Zn2的势参数A和b分别取自于文献[20]和文献[7]。由组合规则得到的Zn-RG系统的色散系数C6、C8和C10也列于表1中。图1给出了由(1)式描述的Zn-RG系统全程区域的TT势曲线,由曲线以及(11)-(13)式得到的各分子光谱参数Re、De、ωe、ωeχe、Be和αe列于表2中,并与先前结果进行比较。
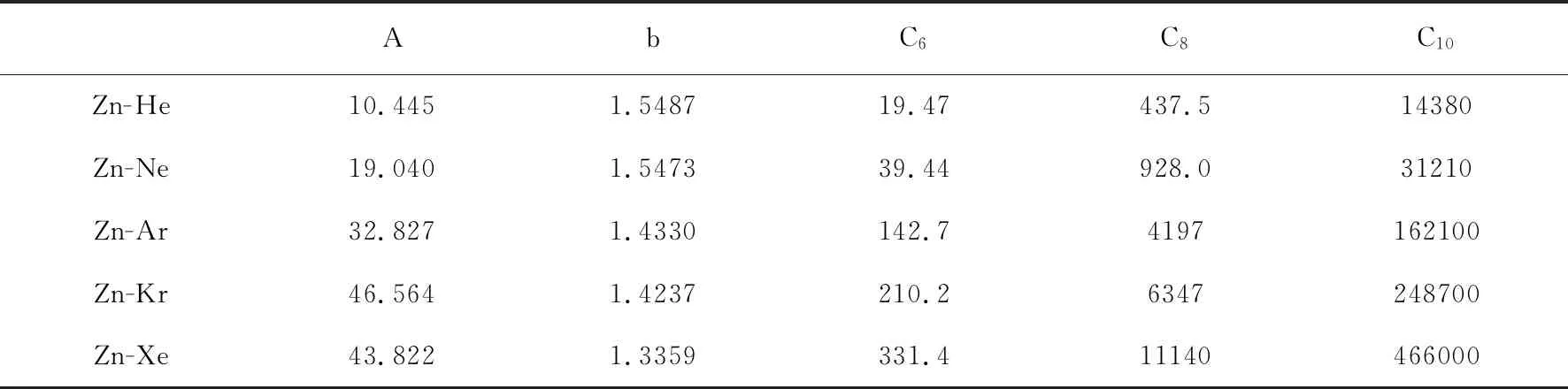
表1 Zn-RG系统各分子的TT势参数(单位:a.u.)

图1 Zn-RG系统各分子的TT势曲线
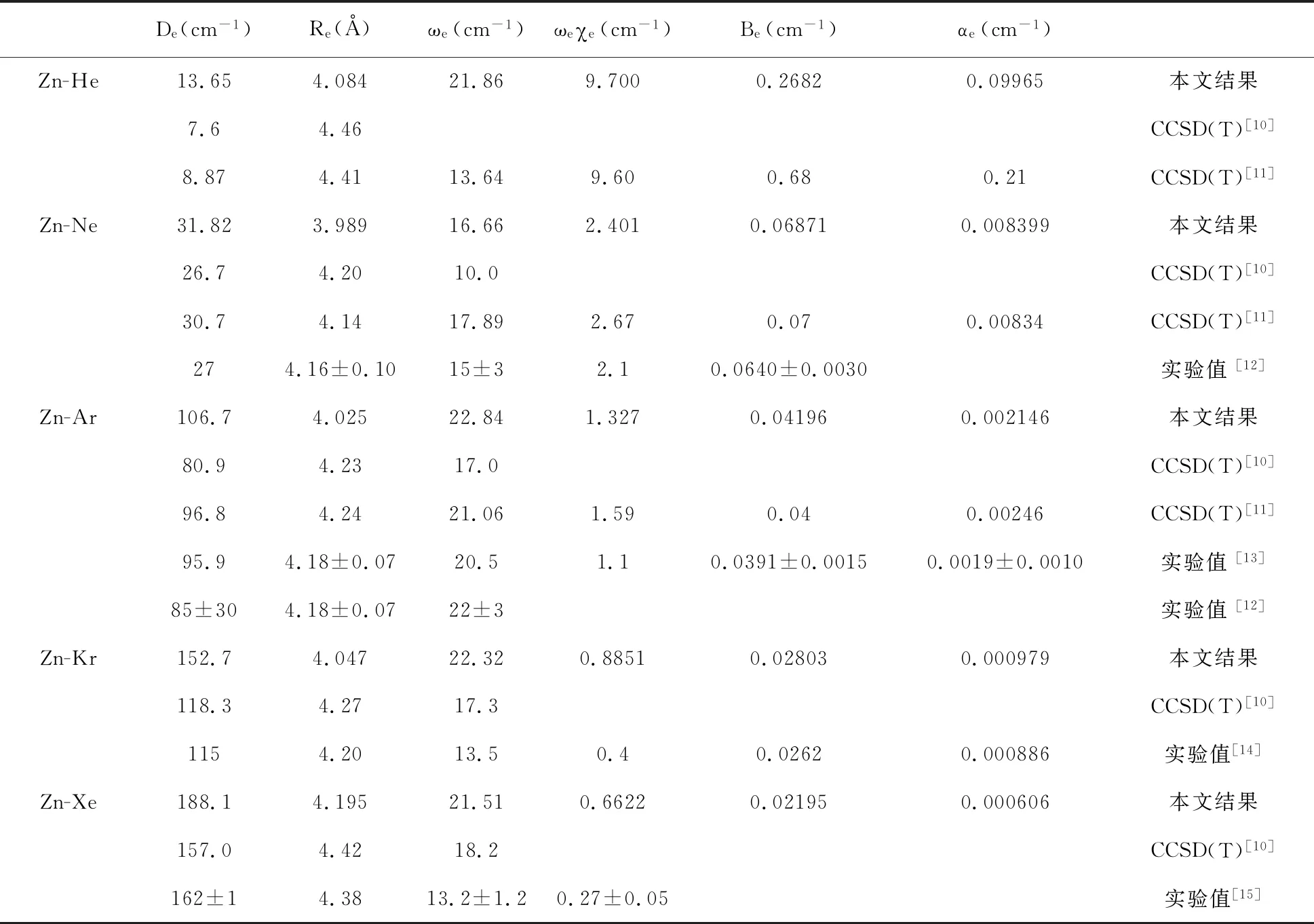
表2 Zn-RG系统各分子的光谱参数
在上述各图表中可以看到,Zn-RG系统分子的势阱深度De随着稀有气体原子从He到Xe极化率的增加而增加,平衡位置Re随着稀有气体原子尺寸的增加而稍有增大(Zn-He除外),这样的变化趋势与文献[10]中CCSD(T)结果的趋势类似,唯一不同的是文献[10]中Zn-He的Re值比其它四个分子的Re值都大,而本文结果中Zn-He的Re值仅比Zn-Xe小些。在表2中列有两组耦合簇CCSD(T)计算结果。在Czuchaj的CCSD(T)[10]计算中,Zn20+和RG8+核由赝势表示,只严格计算了Zn的20个电子和RG的8个电子。而在最新Bera的CCSD(T)[11]计算中,严格计算了Zn和RG的所有核外电子,以更高的精度考虑了电子相关和相对论影响。从这个角度上来说,Bera的计算结果更为接近Zn-RG分子真实的结果。对于Zn-He、Zn-Ne和Zn-Ar分子的De值,Bera结果比Czuchaj结果都要大些,考虑到Bera的CCSD(T)计算中也包含必要的近似处理,所以我们猜测Zn-RG的真实De值比Bera结果还要大些,本文结果也确实如此。
由于Zn-He分子的结合能相当地弱,表2中Zn-He分子各光谱参数数据之间的差距较大,我们得不到任何明确的结论。对于Zn-Ne分子,本文Re和De结果与Bera的CCSD(T)[11]结果基本一致 ,Re小3.6%,De.6%。Zn-Ne分子的实验结果,是McCaffrey激光诱导荧光光谱实验值[12],本文ωe=16.66 cm-1在McCaffrey给出的实验范围15±3 cm-1内,其它的光谱参数结果也基本符合。对于Zn-Kr和Zn-Xe分子,各结果之间存在差距,但是本文De值结果符合我们预测的变化趋势。
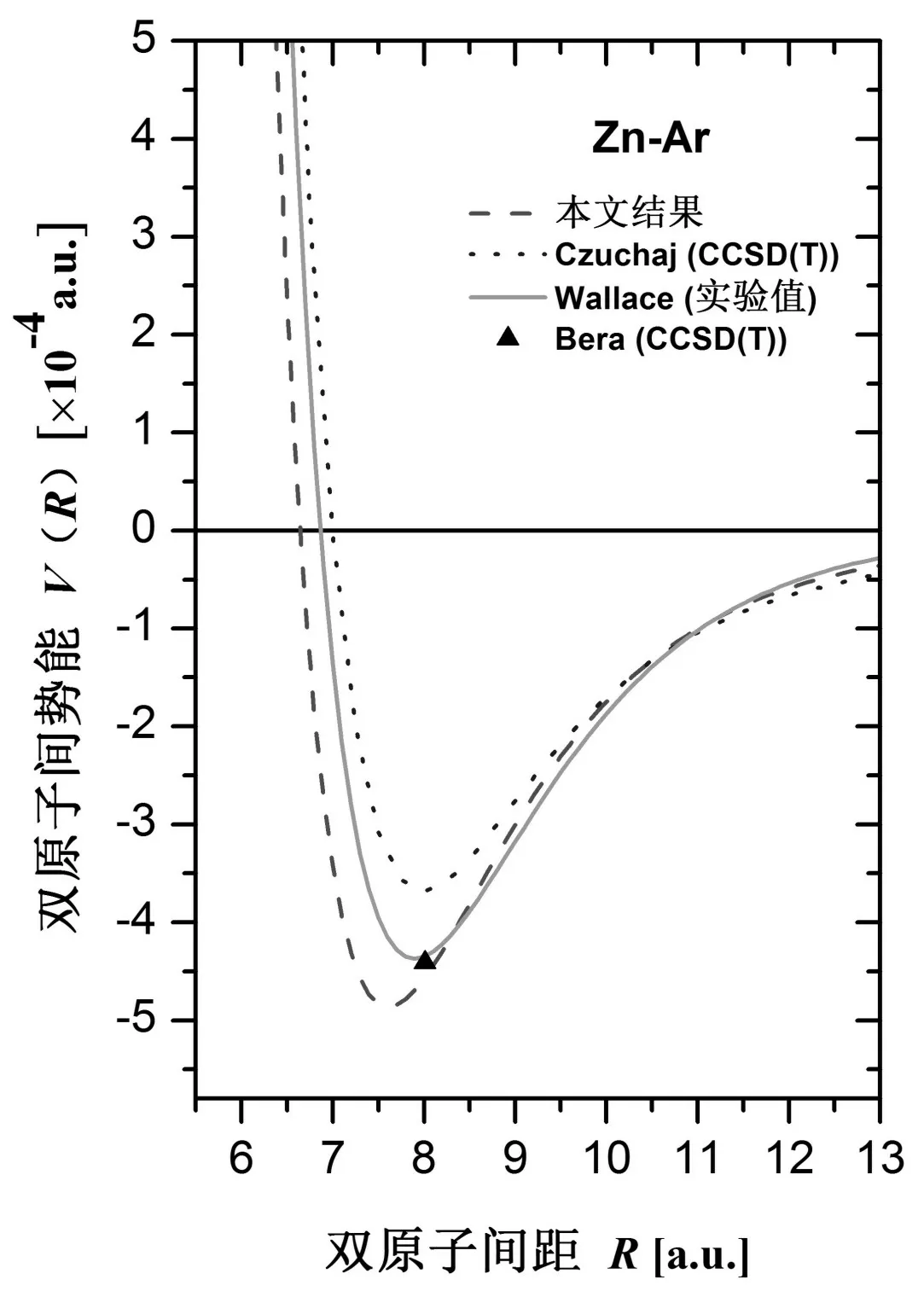
图2 Zn-Ar分子势能结果比较
在Zn-RG体系所有的分子中,关于Zn-Ar分子的研究是最多的。图2是关于Zn-Ar分子的本文结果与先前结果比较。其中,Wallace用Morse函数(De=95.9 cm-1、Re=4.18 Å、β=1.273 Å-1)拟合的激光诱导荧光光谱实验结果[13],Morse函数形式为:
V(R)=De[(1-e-β?(R-Re))2-1]
图2中的三角表示Bera的CCSD(T)结果[11]。图2中最大的差距是Czuchaj给出的势阱深度De要比本文的浅24%,由前面的分析可知这样的差距也并不奇怪。本文De=106.7 cm-1值在McCaffrey给出的实验结果85±30 cm-1范围内[12],其它光谱参数结果也基本符合。
3 结论
本文利用TT势参数的组合规则,用TT势模型计算得到了Zn-RG体系各分子基态的van der Waals势,并给出了各分子的光谱参数。本文得到的势能曲线与其它实验结果都具有可比性,Zn-He、Zn-Ne、Zn-Ar分子的结果与Bera的CCSD(T)结果[11]符合的较好。
本文的计算方法优点之一是无需使用任何实验数据,另一优点是TT势在任何地方都是连续的,各阶导数都存在,可以方便地用于需要解析扩展到复平面的理论。本文计算结果的精确性还可以进一步提高,可以考虑从以下几个方面入手:(1)提高Zn极化率的精确性;(2)得到Zn-RG体系分子更为准确的色散系数;(3)寻求更为准确的参数b的组合规则,能够适用于两原子尺寸相差较大的双原子分子。