大跨越导线微风振动波的色散关系分析

陈晓娟， 王璋奇

(1.华北电力大学 能源动力与机械工程学院，河北 保定 071003； 2.内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

0 引 言

微风振动是架空导线发生最为频繁的风振之一，长时间的高频微幅累积运动，使得架空线常常在高应变点发生疲劳断股、甚至断裂，威胁导线的使用寿命和线路的运行安全[1]。对导线微风振动的认识与研究由来已久，从对导线结构模型的描述来看，主要经历了二维静止圆柱[2]和强迫振动圆柱的尾流特性研究[3]、到弹簧振子模型的强迫振动特性分析[4]、均匀流中刚性节段模型的尾流特性[5]和涡激振动特性[6]研究，到现阶段考虑空间相关性的长柔性结构模型的微风振动特性研究[7-9]，这一过程也体现了对导线微风振动认识的逐步深入和技术手段的提高。

大跨越导线的几何结构具有典型的长柔性圆柱结构特点，长径比(单档导线长度和直径之比)高达104～105，同时架空导线一般采用多股细金属丝绞合而成，刚度对其悬挂空间曲线形状影响很小，一般来说承受拉力而不能承受弯矩[10]。研究导线的微风振动特性时，常常采用一维连续弦模型[9，11]描述其结构运动特性。对外界激励的响应分析一般采用振动模态法或行波法。前一种方法将驻波视为振型，将结构的振动看作是各阶振动模态的叠加；后一种方法将振动视为弹性扰动在结构介质中的传播，形成结构行波力学模型。振动模态法忽视了扰动传播速度的有限性，对大型结构、柔性结构等计算结果偏差较大[12]。而行波法不仅能直接给出结构的固有频率、振型和瞬态响应，还可以有效地研究结构系统在边界、接头等不连续处的能量传递规律以及阻尼结构中波的衰减吸收等，更符合动力响应的物理本质，因而在研究长柔导线微风振动特性时表现出优越性。

国内外对结构振动波特性开展了一些研究工作，大多局限于与实波数相关的波。文献[13]对复合材料层合板在冲击载荷作用下的瞬态波动特性开展了研究。文献[14，15]从不同角度对梁模型中振动波的建模、传播特性及其主动控制进行研究。

色散关系反映了结构模型振动的共同特征，决定了所描述系统自由运动的模态，而且在强迫运动中也会包含这些自由运动的模态。长柔导线系统的固有频率非常密集，因而尾流漩涡脱落与结构频率的锁定，往往形成的是多模态[16，17](一定频率带宽范围)的锁定，即锁定区的风激励可看作多个不同频率简谐谐波的傅里叶叠加形成。因此在研究导线微风振动锁定后的波动问题时，锁定区振动所形成的横波在导线中的传播、衰减、色散特性可首先借助结构的色散关系进行定性分析。国内对输电线路风振横波色散规律的研究相对缺乏，尤其是对典型长柔导线模型色散关系的全面研究和对比分析，而根轨迹法可清晰直观地反映出系统参数变化时，特征根在复平面内随参数变化的移动轨迹，从而成为掌握和控制结构系统性能的重要途径。

综上，为全面认识连续弦模型在导线微风振动中的应用，本文建立典型导线模型的横向运动方程，退化形成4中典型模型的色散关系；明确复波数虚、实部在导线微风振动波研究中的物理意义；引入根轨迹法，绘制复平面内4种模型色散关系的移动轨迹图，分析复波数的虚、实部随频率和阻尼的变化规律，讨论振动波在几种典型结构模型中的传播和衰减规律，以及波速随阻尼和弹性刚度的色散规律，为架空导线微风振动波特性的研究提供基础理论。

1 色散关系的推导

1.1 基本假设

(1)导线为均匀实体，不考虑导线各股之间的间隙和不连续性。

(2)导线内任意点的几何变形可以利用其心形的位移和横截面的转动来表示。并假定变形前其心形线是一条直线。

(3)导线材料为粘弹性。

(4)在导线变形过程中，横截面保持平面，并始终垂直于变形后的心线。

(5)对于导线的面内运动，假设变形过程中，导线始终处于x-o-y面内，且满足小变形条件。

1.2 色散方程

基于架空导线的长柔性结构特点及微风振动的小位移特性，在上述假设的基础上，将架空线简化为没有抗弯刚度的柔性弦，其微风振动横向运动的控制方程表示如下：

(1)

式中：y为空间位置x处t时刻系统响应；T为水平张力；m为单位长度的质量；c为线性阻尼系数；k为等效弹性刚度；f为风激励力。

假设方程中各系数均为恒值，将系统的行波解

y(x,t)=Aei(γx-ωt)或y(x,t)=Aeiγ(x-ut)

(2)

带入式(1)中，可得系统的色散关系如下：

Tγ2-mω2-icω+k=0

(3)

式中：γ为横波的波数，反应波在空间的传播特性；ω为角频率，反应波的时间特性；u为波速，u=ω/γ,单位时间内波的相位传播速度；A为振动波的幅值。

色散关系将外部扰动在结构中形成的横波的波数(或波长)、波速、频率建立了联系，可将波数看作波频的函数或将波速看作波数的函数，求解色散式(3)将得到一组波数(速)解，它由频率ω、阻尼c和结构本身的属性决定，表示为

(4)

或

(5)

由式(3)知，弦模型的色散关系为二阶方程，故存在两种符号相反的波数(速)，响应横波由两种可能波动分量叠加形成。接下来讨论用复波数γ来判别波动行为，以此作为模型微风振动行波解的分析基础。

2 色散方程的物理意义

如式(4)所示，波数一般来说是复数。不失一般性，将色散方程解出的波数表示为γ=a+ib(a、b为实数)，带入行波解(2)，可得y(x,t)=Ae-bxei(ax-ωt)，讨论复波数实部和虚部的取值：

(1)当a≠0，b=0时，波数γ为实数。y(x,t)=Aei(ax-ωt)。

在一维弦中，扰动以波的形式沿正负两个方向传播，传播方向由波数的实部决定。实部a>0和a<0分别表示沿-x方向和+x方向行进的传播波，波的相位传播速度u=ω/|a|。

(2)当a=0，b≠0时，波数γ为虚数。y(x,t)=Ae-bxe-iωt。

从数学意义上，b表示系统波幅A在空间的衰减或增加，但从物理意义上来看，由于阻尼的存在，横波在行进过程中波幅只能逐渐衰减而不能增大。图1为任意时刻横波在空间x>0时的运动状态，可以看到，在b>0的情况下，y随着传播距离的增加而逐渐减小。当空间长度无限增大(无限远离扰动位置)时，y→0。因此，对于b>0的情形，系统的扰动最终趋于消失，这符合系统在阻尼作用下响应幅值的变化规律，系统趋于稳定。b<0的情况下，系统的运动随着空间的增大而不断增大，不论初始扰动多么微小，系统的扰动都会逐渐增长到非常大的数值，也就是说，一旦受到扰动，系统就永远不可能再回到平衡状态上去了。这样的系统是不稳定的，显然不符合实际导线的运动情况。因而b>0表示向x正方向的消逝波，b<0表示x负向的消逝波，此种情形下的扰动不能在结构中形成波动传播。

图1 系统在x>0时波幅随b的变化规律Fig.1 Variation of amplitude with b (x>0)

(3)当a≠0，b≠0时，波数γ为复数。y(x,t)=Ae-bxei(ax-ωt)。

上述分析知，虚部b>0表示波幅沿+x方向衰减，b<0则对应波幅沿-x方向衰减；实部a>0和a<0分别表示沿-x方向和+x方向行进的传播波。故复波数代表一列向某个方向传播的波同时幅值向特定方向衰减。因此有y(x,t)=Ae-|b| xei(ax-ωt)。其中，A是波的幅值，复波数的虚部|b|是衰减波的衰减因子，|b|越大，单位距离上幅值衰减的程度越大，幅值完全衰减掉所需路程也越短；|b|越小，单位距离上幅值衰减的程度越小，幅值完全衰减掉所需路程也就越长。

3 色散关系的分析

上述分析知，复波数的实部和虚部对扰动在结构中形成的传播波的行为有着明确的物理意义，实部决定了波传播的方向和波长(速)，而虚部表明了波幅在空间的衰减。因此，了解结构特性对波数的影响以及波数随频率的变化对于掌握振动波的传播行为是很重要的。为此将导线的结构模型退化为4种典型模型，如表1所示，分别讨论其色散关系及根轨迹特点。

3.1 无阻尼无刚度模型

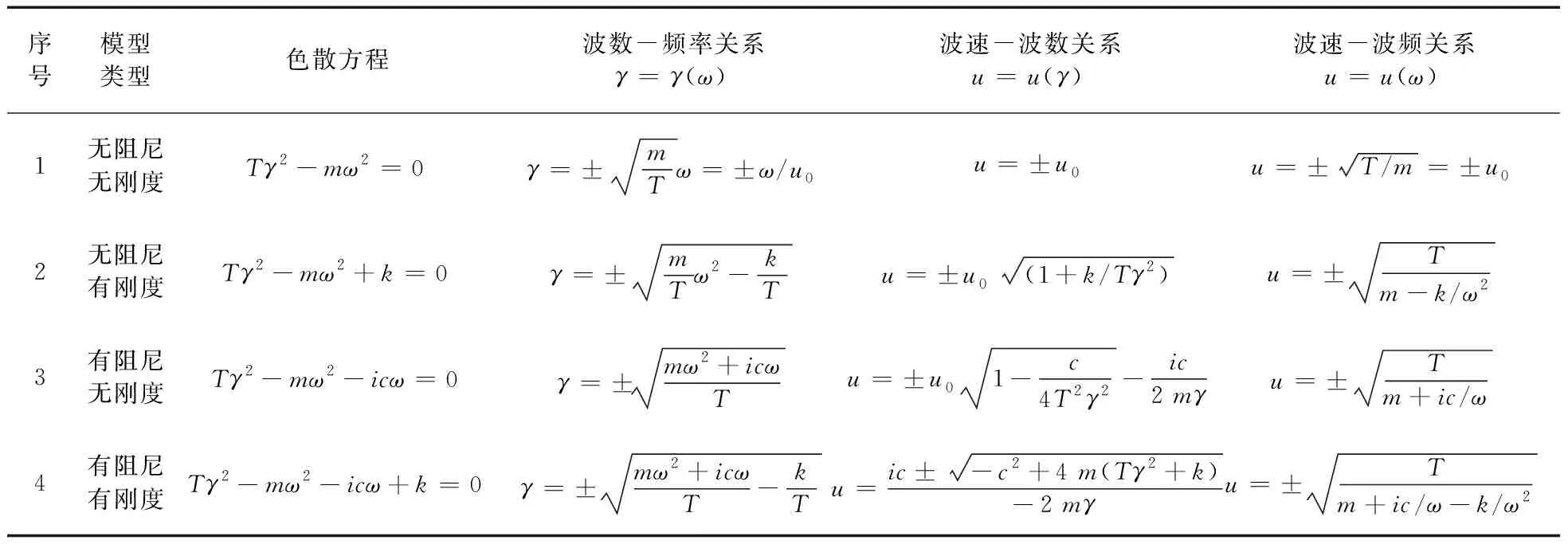
表1 4种典型导线模型的色散关系

根轨迹法是立足于复数域中一套完整的系统研究方法，研究系统某一参数从零变到无穷大时，系统特征方程的根在复平面上移动的轨迹。色散关系的根在复平面内的位置在计算谐激励时的格林函数解时也有重要作用。这里借用根轨迹法来研究复平面内波数随频率、阻尼等参数的变化规律。

图2 无阻尼弦模型中的横波传播示意图Fig.2 Wave propagation in undamped string

经典弦模型在复平面γ域内的根轨迹如图3所示，两个波数分别落在实轴的正半轴和负半轴上，随频率增大波数绝对值相应增大。图中，分别用实线、虚线表示不同根在复平面内随频率变化的轨迹图，箭头方向为频率增加的方向。

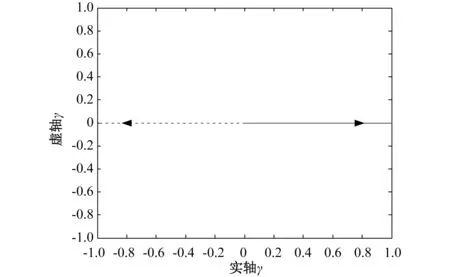
图3 无阻尼弦模型在复γ域的根轨迹Fig.3 Root locus for an undamped string in the complex γ-plane

3.2 无阻尼有刚度模型

ω>ωc，扰动频率高于临界频率时，波数为两个符号相反的实根。结构中存在一对行进方向相反的传播波。

ω<ωc，扰动频率低于临界频率时，波数为两个符号相反的虚根，对应空间幅值变化但不能传播的两列方向相反的消逝波。考虑到分析的目的是判断行波解存在的条件，就本文而言，这个虚波数解不是需要的解，因为它不能在结构中形成传播，但是这个解在瞬时载荷问题和边界耦合问题中有重要作用。

ω=ωc，为结构中横波从传播到不传播的临界频率值，此时对应波数γ=0。模型的运动形式可表示为y=Aexp(-iωct)。此频率下扰动没有引起结构的空间波动，而形成类似于弹簧振子的上下往复运动形态。

为将模型的色散关系更加形象的表达出来，分别绘制了模型的频谱图以及色散曲线，如图4、图5所示。

图4 有刚度弦模型的频谱图Fig.4 Frequency spectrum for a stiffness string model

图5 有刚度弦的色散曲线Fig.5 Dispersion curve for a stiffness string

如图4所示，设定频率ω为正实数，波数γ在实平面内曲线分支为双曲线，虚平面内的分支曲线为椭圆线。实平面内的两条直线(虚线)表示k=0时经典弦的频谱曲线。由u=ω/γ知，相速度恰为频谱曲线任意一点与原点连线构成的斜率，而经典弦模型的直线频率图也表明该模型无色散现象出现。

频谱曲线能够较好的反映出模型的色散特性，而实际关心的仅是波数的虚实和正负，根轨迹图能较好地反映出这样的特性。故下文仅分析模型在复γ平面内的根轨迹特性。如图6所示，实线为正根，虚线为负根，箭头方向为频率增大的方向。随着频率的增大，逐渐超过临界频率时，两个根从虚轴转向实轴，临界频率ω=ωc为图中的交汇点。如图中实线所示，随频率增大，正虚根(波数)绝对值逐渐减小趋近于零，当ω>ωc时，波数转向正实轴，随频率增大波数绝对值逐渐增大；虚线所示波数情况类似。显然，无阻尼有刚度模型，随频率变化导线模型的波数均落在实轴或虚轴上，为纯实数或纯虚数，振动波的传播特性对应第2节中色散方程物理意义的前两种情形。

图6 有刚度弦在复γ平面内的根轨迹图Fig.6 Root locus for a stiffness string in the complex γ-plane

3.3 有阻尼无刚度模型

上述分析中认为能量守恒，当考虑振动波在传播过程中的能量耗散时，根轨迹将在复平面内发生扭曲，这里仅考虑恒定阻尼模型。

实轴(Reγ=0)两侧的两条轨迹线分别对应于不同的阻尼c条件，从图7中知，当阻尼增大时，波数的虚部绝对值增大，意味着波幅在空间的衰减效应显著。阻尼恒定时，箭头方向表示频率增大的方向，从图中来看，低频阶段，频率增大，虚部数值快速上升，意味着低频时，振动波空间幅值的衰减效应明显，且与频率变化关系密切；而高频时，振动波的波数基本恒定(阻尼恒定时)，高频振动波幅在空间的衰减不再受波频的影响。

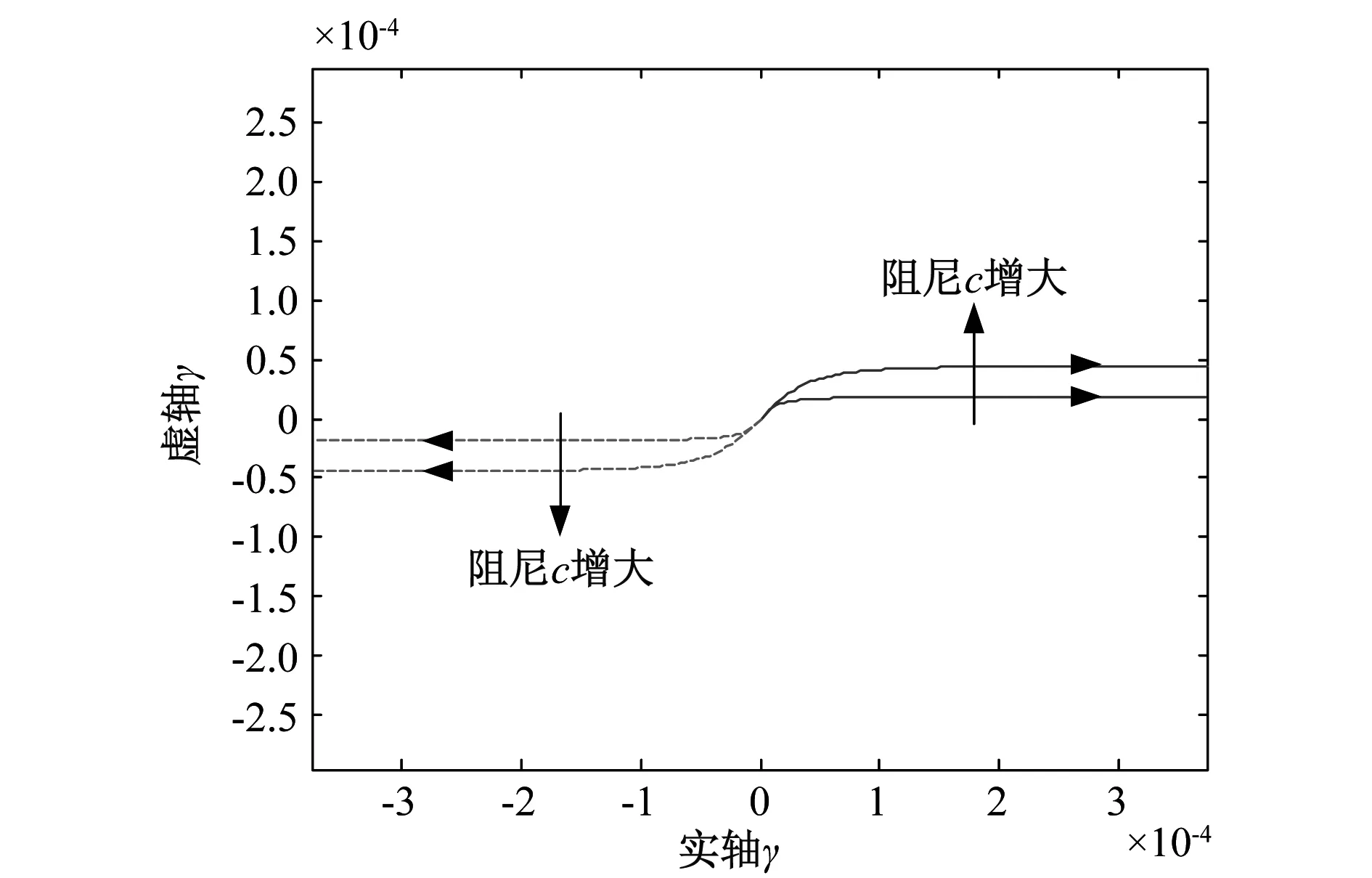
图7 有阻尼弦在复γ域内的根轨迹Fig.7 Root locus for a damped string in the complex γ-plane

由表1知，大部分频率范围内(尤其是高频时)，γ→∞，u→u0，阻尼对结构的色散现象影响很小，就导线的小阻尼和高频振动特性而言，阻尼对结构色散关系的影响可忽略不计。

3.4 有阻尼有刚度模型

图8 有阻尼有刚度弦模型在复γ域内的根轨迹Fig.8 Root locus for a damped stiffness string in the complex γ-plane

4 结 论

基于大跨越导线横向微风振动的线性方程，应用行波法，构造了弹性扰动在结构介质中传播的形式解。推导了考虑弹性刚度和系统阻尼的导线横向振动方程的色散关系，讨论了四种典型结构中波的传播、衰减特性和色散规律，分析了弹性刚度和阻尼对其产生的影响。

(1)波数、频率以及波速构成的色散关系决定了结构中横波的传播特性。就本文构造行波解，复波数的实部决定了波传播的方向和波长，虚部决定了波幅在空间的衰减特性。

(2)所建模型中弹性刚度和系统阻尼对扰动在结构中产生的振动波的传播、衰减和色散特性有显著影响。

(4)阻尼是结构中振动波衰减行为的控制参数。有阻尼无刚度模型中的横波为沿正、反方向的衰减传播波，阻尼的增大使得波幅在空间的衰减效应显著，阻尼对结构色散现象的影响不大；由于阻尼的存在，有刚度有阻尼模型在实频域范围内不存在明确的波传播模式发生转变的临界频率ωc，但存在相似的波动变化趋势。