β射线在铝膜及空气中的衰减

王思广，付孟婷，贾春燕

(北京大学 物理学院 核物理与核技术国家重点实验室，北京 100871)

β射线在穿过物质时可以通过以下过程损失能量：在介质内不断产生电子-离子对的电离作用消耗其部分或全部动能，即使穿过的介质非常薄，通常也有能量衰减；β射线可能被原子核和电子的库仑势散射，在损失能量的同时还将影响自身的运动方向；当β射线受介质库仑场作用做减速运动时，一部分动能会通过韧致辐射以光子的形式发射；如果β射线本身的运动速度超过光在当前介质中的传播速度，则可通过切伦科夫光的形式损失动能[1]. 开设β射线在铝膜及空气中的衰减实验的目的是研究β射线在介质中的行为，培养学生实验技能的同时帮助学生掌握β射线与介质的作用特点. 在北京大学物理学院原有“用β粒子检验相对论的动量-动能关系”的近代物理实验的基础上进行拓展[2]，在测量(准)单能β射线穿过不同厚度的铝片的质量衰减系数的过程中，除了观察计数率随吸收片厚度的变化，还可以让学生分析峰位和半高全宽(Full width at half maximum, FWHM)随铝片厚度的改变. 通过对比分析β射线穿过的真空盒内抽真空及不抽真空2种模式下探测器给出的信号计数率的变化，可计算出空气对不同能量的β射线的衰减长度. 学生在进行能谱分析的过程中涉及到本底扣除、信号峰位拟合、信号峰双侧拟合提取半高全宽信息等一系列能谱分析操作.

1 实验测量方法

β衰变是放射性原子核放射电子(β粒子)和中微子而转变为另一种核的过程[2]. 因为释放出的衰变能Q在反冲核、β粒子及中微子3个粒子之间分配，所以每个粒子所携带的动能并不固定，因而β粒子的能谱是连续的. 为了得到准单能的β射线，通过磁场对连续分布的β粒子束进行偏转，根据均匀磁场中动量p与偏转半径r之间的关系

p=eBr，

(1)

在不同偏转位置处可挑选出不同动量的β粒子. 其中,e为电子电荷，B为磁场的磁感应强度.

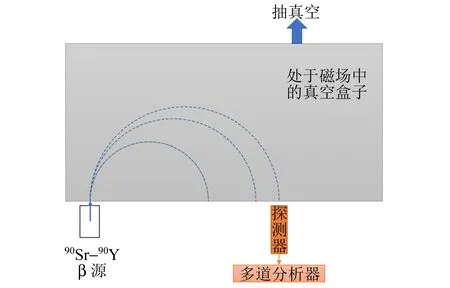
图1 实验装置示意图

1.1 铝膜对β射线衰减的测量

在出射窗与探测器之间，放入不同厚度的铝膜对狭缝进行遮挡，测量经铝膜衰减后的β多道能谱，研究铝膜对能谱形状的影响[3-4]. 利用60Co及137Cs的γ特征射线对系统进行能量刻度. 拟合各β多道能谱的信号峰给出峰位，得到β粒子的信号峰位随铝膜厚度变化的关系. 通过分析信号峰的半高全宽，可以给出半高全宽与铝膜厚度之间的关系. 通过分析信号的计数率随吸收铝膜厚度的变化，可以计算出β粒子在铝膜中的衰减长度.

1.2 β射线受空气衰减的测量

对于同一出射窗位置，抽真空模式(真空度约0.1 Pa)及不抽真空模式下探测器测得的能谱上信号峰的计数率有明显差异，而引起该差异的唯一来源是真空盒内气体含量的不同. 因为入射窗和出射窗位置已知，故粒子在磁场中经过的路径x已知(外磁场是均匀磁场，且其磁感应强度已知)，从而可以计算出该动能下β射线在空气中的衰减长度.

另外，根据抽真空及不抽真空时信号峰位的能量差异dE，可以给出不同能量的β射线的能损dE/dx测量值.

2 数据处理方法

传统的能谱分析通过本底函数及信号函数[3-8]对多道能谱进行拟合，给出信号峰下的积分计数，通过多道谱仪提供的活时间，可算出计数率. 然而本实验获取的β射线的信号形状严重偏离高斯函数分布，多次数据分析证明很难找到普适的峰形及本底描述函数进行拟合. 其原因为β粒子在经过真空盒、出射窗和NaI探测器晶体前的铝膜时，通过电离效应、库仑散射和韧致辐射等过程会损失能量，从而导致信号峰低能端拖尾比高能端拖尾长，信号峰形状左右明显不对称. 另外不同能量的β粒子穿过不同长度的介质时损失的能量差异较大，使得找到通用模型拟合所有条件下获取的多道能谱变得非常困难.

利用NaI探测器测量的 β射线能谱如图2所示，图中各道计数已经除以活时间. 蓝色细线代表本底计数率的分布，红色点代表信号峰，信号峰左右蓝色粗线为多项式拟合线，用于寻找半高处的位置以计算半高全宽，信号峰顶部绿色细线为高斯函数拟合线.

图2 利用NaI探测器测量的β射线能谱

在实际数据处理过程中利用了半经验模型[9]：假定当前第i道的本底计数率Bi与其右侧的事件积分总和成正比,在图2所示的能谱上信号峰的左侧找到计数率最低点，第l道，作为信号的左边界(图2中左侧红色竖线所对应的位置)，利用在l两侧±3道范围内的各道计数率求出平均高度hl；临时找到信号峰最高处所对应的道址M0(图2内中间红色竖线)，然后在峰的右侧与距离M0为|M0-l|道处找到右边界r道(图2中右侧红色竖线)；利用r道两侧±3道范围内的计数率求出平均高度hr；然后计算出l与r之间各道的计数率之和：

其中，yj是第j道的计数率. 则每道本底计数率Bi为

(2)

有了信号计数率的分布(图2红点表示)，可以用高斯函数通过拟合信号峰上半部，例如±1σ区间范围内(通常信号上半部受拖尾干扰小，接近高斯分布)，给出拟合的峰位M及高度H. 为减少初始选定的拟合区间对拟合结果的影响，实际数据处理中可多次拟合迭代峰的宽度σ及峰位M,给出稳定的拟合结果：给出σ初始值，确定初始峰位M0±1σ拟合范围，进行拟合得到新的σ值及峰位M，利用新的σ值及峰位M值重新给出拟合范围，重复上一步迭代拟合多次，直到宽度σ、峰位M及高度H的前后2次拟合结果无明显变化为止. 最终得到的信号峰上半部拟合曲线如图2中绿色细线所示.

信号峰的半高全宽可以用数字内插方法计算给出数值解[10]：对信号峰左、右两侧半高处附近的数据，分别用多项式进行拟合，如图2内蓝色粗线所示. 借助该连续变化的拟合函数，通过数值扫描的办法寻找出信号高度H的一半所对应的左、右侧半高处的道址Xl和Xr(计算出不同道址对应的拟合函数值，找出函数取值最接近H/2峰高的道址值. 数值分析中扫描步长远小于1道，以确保引入的误差可忽略)，利用|Xl-Xr|可得半高全宽.

峰位M、峰高H等拟合量的误差在拟合过程中评估给出. 但用数值扫描得到的Xl和Xr的误差很难估算，建议利用拟合时峰位的误差进行评估. 也可以采用更为准确的做法：

a.用蒙特卡洛方法根据测量的信号分布形状产生同样统计量的数据；

b.对产生的数据进行相同的数据处理方法获得半高全宽；

c.多次重复步骤a和b，得到半高全宽的分布的均方根误差值作为误差. 该方法常应用于高能物理数据分析[11].

3 不同厚度的铝膜对准单能β射线吸收后的能谱分析

在出射窗与探测器之间加入不同厚度的铝膜，获取真空盒处于抽真空状态的能谱. 谱仪能量刻度使用137Cs(反散射峰184.323 keV和特征γ射线峰661.660 keV)及60Co(特征γ射线峰1 173.237 keV和1 332.501 keV[12])给出. 不加铝膜时和加厚度为100，200，300 μm的铝膜时的能谱如图3所示，图中每道计数都除以了能谱获取的活时间.

图3 NaI探测器测量的同一测量位置加不同厚度的铝膜后的β射线能谱(不同颜色的细实线)及扣除本底后的信号形状(不同颜色的虚线)

通过图3，让学生至少给出如下3项数据处理结果：

1)从图3可得，随着吸收膜厚度的增加，β射线峰的峰位逐渐向左移动(作为比较，也可让学生测量观察137Cs或60Co源的特征γ射线峰的峰位随着吸收膜厚度的增加其峰位是否移动)，参考图2所示的数据分析方法，扣除本底后拟合出峰位M的能量随吸收铝膜厚度的变化(可给出峰位的绝对数值或峰位与无外加吸收铝膜时的峰位的差值随铝膜厚度的变化图)结果如图4所示,直线拟合的斜率为(-406±52) eV/μm. 图4各点对应的峰位数据进行了探测器内NaI晶体前200 μm铝膜对β射线动能影响的修正，所用修正数据来自于文献[2]. 根据图4，可明显看出随着铝吸收膜厚度的增加，峰位的能量减小值逐渐增大[9].原因是β射线穿过的铝吸收膜厚度越大，通过电离和韧致辐射等过程损失的能量越多.

2)从图3也可以定性得出:随着铝吸收膜厚度的增加，β射线峰的峰宽也逐渐变大. 参考图2所示的数据分析方法，扣除本底后可以拟合出峰的半高全宽随吸收铝膜厚度的变化，结果如图5所示.

图5 信号峰的半高全宽随铝膜厚度的变化

由衰减长度LAl可推出

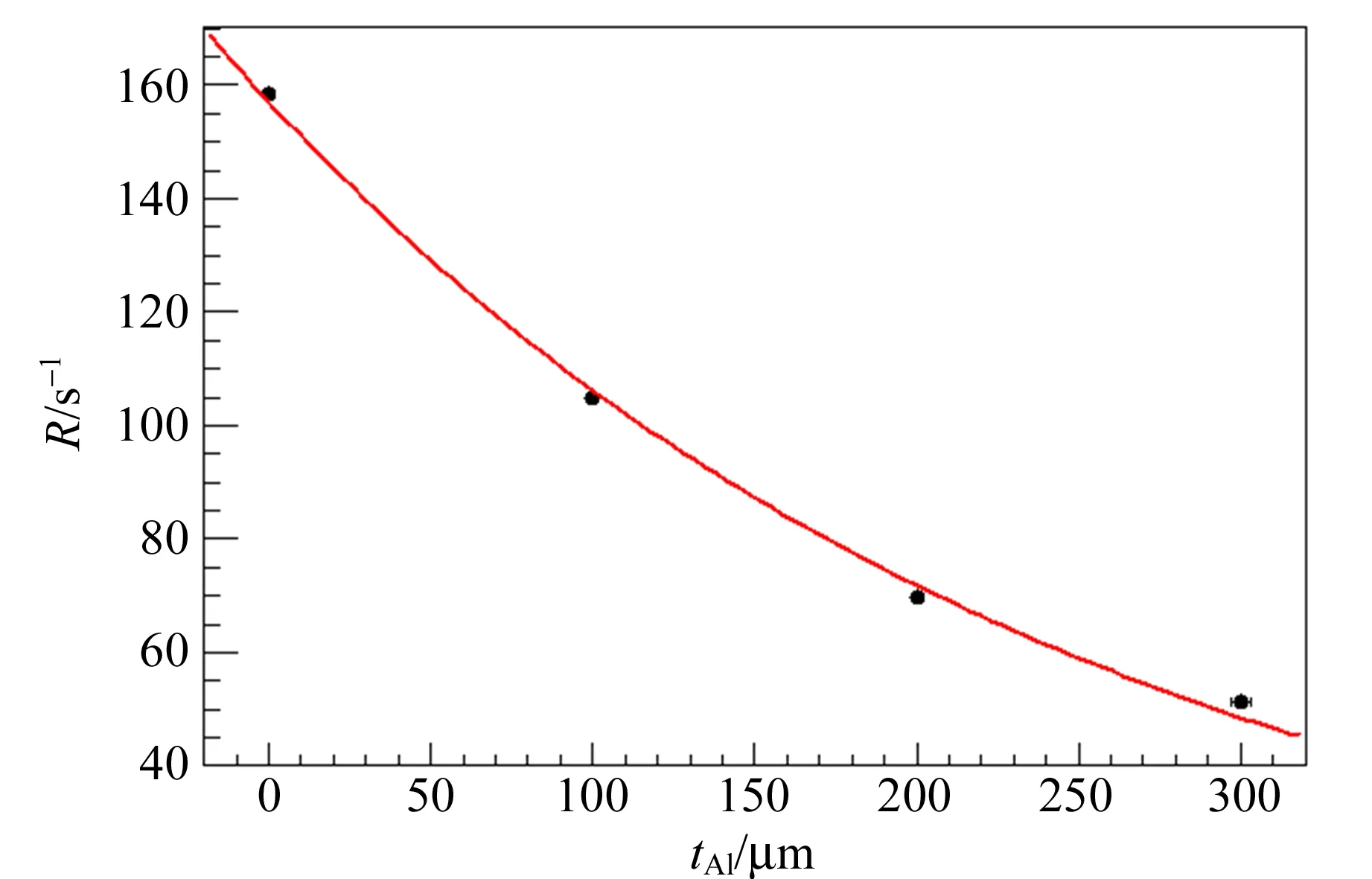
图6 计数率随铝吸收膜厚度的变化

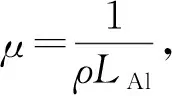
(3)

其中，ρ为吸收膜的密度，这里吸收膜材质为铝，其密度值通常取2.7 g/cm3.

4 空气及真空下准单能β射线能谱的分析

如果真空盒内充满空气，部分β粒子在穿过磁场的过程中会与空气发生作用，可能会偏离出既定轨道或损失较多的能量，从而穿过出射窗口探测器测得的计数率相对于抽真空的模式下测得的计数率要少. 通过比较同一窗口真空模式下测得的信号计数率RV及不抽真空的情况下(1标准大气压下)的计数率RA，并假设衰减长度与真空盒中的气压成反比，即

(4)

图7为不同出射窗口测量的能谱. 每个窗口的能谱获得方式分为抽真空(虚线表示)与不抽真空(1标准气压下，实线表示)2种模式,各出射窗对应的β粒子在均匀磁场中的轨道直径用D示出. 磁感应强度B为6.555×10-2T. 比较2种模式下的信号强度，可以看出是否抽真空对计数率的影响. 利用真空盒抽真空时测得的信号计数率RV及不抽真空时测得的信号计数率RA，以及已知在均匀磁场中β粒子束所经过的径迹长度x，可计算出衰减长度LA[11].

图7 在真空盒的不同出射窗测量的能谱分布

图8为空气对于不同能量的β射线的衰减长度，其中动能根据磁感应强度及偏转半径计算，衰减长度根据真空盒中有无抽真空时的计数率的变化计算，各点误差棒由计数率及路径长度的统计误差传递计算. 可以发现，能量越大其穿越能力越强，即衰减长度的数值越大.

图8 空气对不同动能的β射线的衰减长度

比较同一窗口有无抽真空时峰位的变化，可以计算出动能差异，根据已知的径迹长度x，可以算出β粒子在空气中单位长度的能损为

(5)

其中EA和EV分别是空气及真空条件下测量得到的信号峰的峰位能量. 不同动能的β射线在空气中的dE/dx测量结果如图9所示. 其中β射线的动能是由β粒子在磁场中的偏转半径及所加外磁场的磁感应强度计算而得，蓝色实心圆对应的数据为NaI探测器直接测量计算得到的单位长度的能量损失dE/dx，红色空心圆对应的数据为经过NaI探测器探头本身的铝膜及真空盒有机膜出射窗修正后的动能差计算出的dE/dx. 误差棒由拟合的峰位误差传递所得.

图9 不同动能的β粒子在空气中的能量损失

可以发现在观测的动能范围内，β射线穿过单位长度的空气后损失的动能随射线动能的增加而增加(损失为负值，绝对值越大表示经过单位长度的空气后β粒子损失的能量越大).

β粒子穿过铝膜及有机膜的修正所用的数据表见文献[2]. 从图9中可以发现，是否修正探测器结构本身的铝窗和真空盒的有机膜出射窗对dE/dx的数值影响不大.

另外，根据dE/dx，利用干燥空气中每产生1个电子-离子对所需要的能量约为33.85 eV[13-14]，推算出1个β粒子在真空盒中沿径迹电离的电子-离子对数目.

5 结束语

利用既有的用β粒子检验相对论的动量-动能关系的实验装置，不添加任何装置即可引导学生进行β准单能束在空气和铝吸收膜中衰减长度的测量，分析能谱可以给出不同能量的β粒子在空气中单位长度的能损dE/dx，铝膜对β粒子能量的衰减系数以及信号峰的半高全宽随吸收铝膜厚度的变化. 通过实际测量以及数据处理，学生得到科研训练的同时，对β粒子与物质相互作用的性质应有更加深刻的理解.