动态法测量杨氏模量实验中的弹性各向异性

章 越，王家宝，亓山山，白在桥

(北京师范大学 物理学系，北京 100875)

杨氏模量的测量方法可分为静态法和动态法，其中静态法通过测量样品在外力下的形变进而求得出杨氏模量，最近有许多文献讨论用不同的方法测量微小位移[1-2]；动态法是根据样品的共振频率推知样品的弹性参量[3-4]，通常的操作是，调节激发信号的频率，用示波器或交流电压表观察振动信号的幅度，找到最大振动对应的共振频率. 但实验中有时会发现存在2个间隔很近的共振频率[5]，这种“双共振峰”现象不仅会影响量结果的准确性，还会造成学生对实验原理的困惑. 实验中观测细圆柱形样品的横向振动，由于横波具有偏振性，至少会涉及到2个振动模式. 只要样品的弹性力学性质不是严格各向同性的[6]，绕样品中心线的旋转对称性就不再保持，这2个模式的频率就会有所不同. 因此出现2个共振峰并不意外. 此外，实验采用的悬挂测量方式还会引入各向异性. 已有论文对悬挂造成的影响进行了讨论[7]，本文将综合考虑这2种各向异性的影响，以期能够定量理解“双共振峰”现象，并在此基础上给出更合理的杨氏模量计算方法.

1 理论分析

动态法测量杨氏模量的振动系统如图1所示. 待测圆杆样品被2根棉线水平悬挂起来，悬挂点相对杆的中心左右对称. 一根悬线将激振器的激励信号传至样品，另一个悬线将样品的振动传回拾振器，用于监视和测量样品的振动. 为方便分析，在样品截面内建立O-xyz坐标系，其中O为杆的几何中心，x轴指向下，y轴水平，z轴与样品的中心线重合.

图1 坐标系示意图

杆的横向振动在x-y平面内，先假设杆的力学性质具有完美的旋转对称性，并暂时忽略悬线的影响. 这样x方向和y方向的振动频率和模式完全相同，在细杆近似下，由欧拉-伯努利梁理论可知共振频率为

(1)

其中,L,I和ρ分别为杆的长度、面矩和线密度，E为材料的杨氏模量，ξk是cos (ξ)cosh (ξ)=1的

第k个正根(ξ1=4.730 040 7…).ωk,0对应的振动模式为

(2)

一般地，x方向的振动位移φx(z,t)和y方向的振动位移φy(z,t)都是不同本征振动的叠加：

(3)

现在考虑杆各向异性的影响. 由于只关心基频附近的振动，假定振动可以写为

(4)

这样假设相当于在瑞利-里兹方法(Rayleigh-Ritz method)中选取2个简并的基频模式作为基函数[8]. 杆的振动被约化为2个自由度{cx,cy}的运动. 对各向同性的情况，杆的动能可表示为

(5)

势能可表示为

(6)

(7)

式(7)假定了x轴和y轴是弹性的主轴. 对于一般的悬挂角度，势能应写成

(8)

(9)

式中θ为弹性主轴与x轴的夹角.

(10)

(11)

其中质量矩阵

(12)

根据动能和势能的表达式，利用欧拉-拉格朗日方程，可得2个本征振动频率为

(13)

其中λ1,2为M-1/2KM-1/2≡Q的2个本征值. 保留到1阶小量，

(14)

其中

(15)

表征了悬线对振动总的影响. 因此保留到1阶项，有

(16)

1)θ→θ+π，共振频率保持不变.

2)2个共振频率的平均值

与θ无关.

3)2个共振频率的差值为

其最小值为||δ|-Δ|ω0，在|δ|增大的过程中先减小到零，然后增大. 只有|δ|=Δ且θ=0,π时才会有ω1=ω2. 这与量子力学中的能级回避交叉的数学原理相同[9].

4)如果|δ|≫Δ，

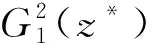
此外，只要x轴不是弹性主轴，x方向的运动就包含了2个本征模式分量，加在x方向的激励就可以激发出2个本征振动，拾振器在x方向的也可探测到这2个本征振动信号. 因此双共振峰应该是常见现象. 但是当sin (2θ)≈0或|δ|≫Δ时，Q的1个本征向量与x轴夹角很小，2个共振峰的高度会相差很大，双共振峰现象不明显.

2 实验装置与方法

本文实验装置与文献[5]相同，包括动态法杨氏模量测定仪(杭州大华DHY-2)、信号发生器(普源精电DG1032Z)、数据采集卡(NI-myDAQ)和装有LabVIEW软件的计算机，其中信号发生器有USB-device接口，可以用LabVIEW控制输出参量. 测试杆长度约180 mm，直径约为6 mm. 与文献[5]中的实验不同，这里需要测量样品的角度. 用低成本显微摄像头监视样品的端面，并通过LabVIEW显示在屏幕上，得到直径约为300像素的圆形(见图2). 在杆的端面上刻记号，作为角度的零点. 同时在图像上叠加等角度间隔的分划线，便于把悬挂角度调整到预定值.

图2 样品端面照片以及角度刻线

实验通过LabVIEW编程扫描信号发生器的输出频率用于激励测试杆的振动，使用数据采集卡获得每个频率下拾振器的输出信号，得到样品振动的幅-频和相-频特性曲线. 所得曲线用双共振模型拟合，得到2个共振频率及其宽度. 程序控制和数据拟合的细节参见文献[5]. 由于共振频率具有θ→θ+π的不变性，为了缩短测量时长，实验中θ限制在[0,π]之内. 同时，比较θ=0和θ=π的结果，可以粗略估计测量结果的可重复性.

3 实验结果

首先对1根黄铜杆，在从中心向边缘的8个不同悬挂位置(z*)，分别测量了9个不同悬挂角度(θ)的频率响应曲线. 由于数据量很大，图3只画出了z*=60 mm的9条幅-频特性曲线，可以看出，随θ改变，2个共振峰的位置、宽度和相对高度都会改变.

图3 黄铜杆固定z*=60 mm，不同θ的幅-频特性曲线 (从上到下θ从0°均匀增大到180°)

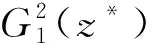
注意实验中θ的零点是根据样品端面上的记号确定的，很可能并不对应杆的弹性主轴(即固有弹性矩阵Kθ最大特征值对应的特征方向). 如果主轴位置为θ0，式(16)应改写成

(17)

因此用包含{f0,γ,α,θ0}4个参量的公式拟合实测的144个共振频率：

(18)

(19)

需要说明的是，式(18)中f1(f2)指的是2个共振频率中较大(较小)的，而文献[3]是根据共振峰的宽窄来标记不同的频率. 这2种标记并没有确定的对应关系(图3).

表1 黄铜杆不同悬挂位置和角度的共振频率

表2 不同悬挂位置对应的

采用高斯-牛顿方法进行非线性最小二乘拟合，所得最佳拟合参量见表3.

表3 共振频率拟合参量

图4画出了拟合的残差分布. 可以看出绝大部分残差的绝对值都小于0.2 Hz. 由于存在温度起伏、样品定位误差等因素，本实验共振频率测量的可重复性在0.1 Hz量级，因此可以认为拟合结果相当好.

为了对拟合效果有感性认识，图5画出Δf=f1-f2的测量值与计算值的对比. 可以看出理论公式很好地给出了Δf的变化规律.

图4 拟合残差分布统计直方图

图5 Δf测量值(点)与计算值(连续曲线)的对比(为便于展示，从下到上每条曲线的零点依次相对前一条向上平移了1 Hz)

对不锈钢样品进行了类似的测量，同样观察到双共振峰现象，所得测量结果见表4. 由于θ=135°比较接近弹性主轴，频率特性曲线中“双峰”现象不明显，对应测量角度改在了θ=140°. 同样用式(18)拟合，拟合结果与铜杆相当(表3). 这说明本文的理论可以较好地描述一般金属杆由于弹性各向异性导致的共振频率劈裂.

表4 不锈钢杆不同悬挂位置和角度的共振频率

4 总结和讨论

采用合理的假设，利用瑞利-里兹方法计算了杆弹性的各向异性以及悬线约束引起的共振频率移动，所得公式可以很好地拟合实测数据. 这说明简化模型是合理的. 微扰计算的准确性还应归结于各向异性和悬线约束的影响都很小(Δ,δ都小于0.01)，高阶修正可以忽略.

表5 样品在固定角度下线性拟合所得固有频率