大数据中数据挖掘模型的模糊改进聚类算法

李小红 常振云

摘  要： 在大数据的数据挖掘模型中，普遍采用模糊聚类算法进行数据分析。常用的模糊C均值聚类算法即FCM聚类算法，具有较多明显缺点，如抗噪性偏低、收敛速度慢、聚类数目无法自动确定等。常用的增量式模糊聚类方法通常在原有的以一个中心点为集群代表的基础上，改为选取多中心点进行增量式聚类算法的分析。但是，通过这样的算法进行数据分析也存在一定的问题，主要表现在其中心点选择是固定的，灵活性很差。基于以上原因，文中将对原有基础算法做出改进，主要对大数据中数据挖掘模型的增量型模糊聚类算法做出分析，经实践验证，改进后算法切实可行，普适性较强。

关键词： 增量型模糊聚类; 大数据; 数据挖掘模型; 聚类算法; 余弦相似度; 隶属度矩阵

中图分类号： TN911.1?34                       文献标识码： A                          文章编号： 1004?373X（2020）03?0177?06

Improved fuzzy clustering algorithm for data mining model in big data

LI Xiaohong， CHANG Zhenyun

（School of Information Science and Engineering， Tianshi College， Tianjin 301700， China）

Abstract： The fuzzy clustering algorithm is widely used in data mining model of big data for data analysis. The commonly used fuzzy C?means clustering algorithm， also known as FCM clustering algorithm， has obvious disadvantages， for instance， the noise immunity is poor， the convergence speed is slow， and the number of clusters cannot be determined automatically. In the commonly used incremental fuzzy clustering algorithm， multi?center points are selected for incremental clustering algorithm analysis instead of taking one center point as the cluster representative as before. However， there are still certain problems in the algorithm in the process of data analysis， mainly because the selection of the center point is fixed， resulting the poor flexibility. In view of the above， the existing basic algorithm will be improved， and the incremental fuzzy clustering algorithm for data mining model in big data will be mainly analyzed. The practice shows that the improved algorithm is feasible and universal.

Keywords： incremental fuzzy clustering; big data; data mining model; clustering algorithm; cosine similarity; membership matrix

0  引  言

社会在不断发展和进步，信息时代的到来既让人们享受到了应有的便利，同时也遭受大量信息侵袭的困扰[1]。因此，如何在繁多的数据之中快捷、高效、精确地选取有用信息，成为当下亟需解决的问题。在大数据时代，建立数据挖掘模型就是在庞杂的数据当中对信息进行挖掘，以达到更为高效的信息筛选与获取的目的。在数据挖掘模型之中，聚类算法作为一种常用算法，主要是将数据进行多个集群划分，通过多个不同集群的相似度对比，进而进行数据的选择。本文研究的主要是大数据中数据挖掘模型的模糊改进聚类算法，也即增量型模糊聚类算法，该算法主要依据最小权重阈值展开。

1  模糊聚类算法

1.1  模糊聚类算法概述

模糊聚类算法是基于模糊数学而产生的一种数学方法，首先对模糊数学进行简单介绍。

模糊数学作为有别于经典集合论中非黑即白的绝对关系的突破性数学分支，对于具有不确定性的复杂数据能够做出精确的分析和筛选[2]。

模糊聚类算法首先通过模糊矩阵来反映研究对象的自身属性，并依据相应的隶属度做出聚类，而后以模糊数学为理论依据和基本算法，确定样本间相互的模糊关系，从而实现精确聚类。聚类也就是将差异化较小的数据划为一类，而各类之间的差异程度要尽量明显。

距离矩阵的数学定义是包含一组点间两两相互距离的矩阵，当空间中给定了[M]个欧几里得空间中的点时，其距离矩阵为[M×M]的对称矩阵，且其元素均为非负实数[6]。举例来说，二维空间中的点[A～E]，其空间布置与距离矩阵分别如图3，表1所示。

点[A]～[E]在欧几里得空间当中的距离可由3.1.1节当中所给出的距离公式进行计算，进而得到具体的距离矩阵，通过距离矩阵对其数据的相异度进行分析，从而做出类别划分。

一般来说，当整体数据的集合为[S]，数据块的大小为[mq]时，其距离矩阵的流程图如图4所示。

依据流程图，将生成距离矩阵的算法简述如下：

输入：整体数据集合[S]，数据块大小[mq]，数据块序号[q]，参与矩阵运算的集合[K]。

输出：第[q]个数据块的距离矩阵。

1.由整体数据集合以及参与矩阵运算的集合[K]，获得未参与矩阵运算的集合[N]，[N=S-K]。

2. 对集合[N]与数据块[mq]做出大小判断，判断集合[N]是否小于等于数据块[mq]。

3. 若集合[N]小于等于数据块[mq]，则数据[N]中的所有数据组成集合[N1]。

4. 否则，从数据集合[N]中随机抽取[mq]个数据得到新集合[N1]。

5. 令新的参与运算的集合为[K]，[K=K+N1]。

6. 进行集合[N1]中的笛卡儿积计算，同时对笛卡儿积中每两个数据间的距离进行计算。

7. 对所求得笛卡儿积进行矩阵的转换，同时返回矩阵。

8. 结束。

4  以最小权重阈值为依据的增量型模糊聚类算法

4.1  传统增量型模糊聚类算法的局限性

传统的增量型模糊聚类算法的局限性主要体现在选取中心点的方法上。大致可以分为两种：一种是对集群当中的小数据块进行中心点的选取时，中心点的选取数量固定，代表算法如IMMFC;另一种是集群中可作为小数据块代表的中心点在进行选取时，通常只选择权重最大者作为集群的中心点，代表算法如SPFCM。这两类算法在进行聚类时都不具备较好的普适性，下面分别对二者的局限性进行简要分析。

4.1.1  IMMFC算法的局限性

在IMMFC算法当中，对每个集群的中心点数量的选择，都是用户事先规定好的固定数量。其弊端在于，用户无法获取要进行聚类的所有数据块中的整体数据的分布情况，因此，中心点的固定数量的选取要多少才较为合适是无法确定的。

图5a）中，数据对象均匀分布在集群边缘，单个或几个数据对象对于整个集群来说，不具备很强的代表性。只有在图5b）中，集群中心与边缘均存在数据对象的分布，在算法中可以将中心的数据对象选作中心点。用户通常难以确定集群中数据对象的分布情况，因此IMMFC算法在中心点的数量选取上就存在一定的局限性，不具备普适性。

4.1.2  SPFCM算法的局限性

SPFCM算法当中，整体数据在进行小数据块的划分之后，首先对其中一个小数据块进行模糊C?均值聚类，而后将聚类结果当中权重最大的选作中心点，并将此中心点作为加权对象并入下一个数据块中，继续进行模糊C?均值聚类算法。其弊端在于，当集群中全部数据对象的权重都比较小时，即便选择其中代表性最大者，其代表性也不够明显。

如图5a）中，所有数据对象都分布在集群四周，其在集群中的权重普遍较小，无论选择哪一个数据对象作为中心点，其代表性都不强。因此，SPFCM算法同样不具备普适性。

4.2  基于上述问题的模糊改进聚类算法

4.2.1  算法的提出缘由

改进的增量型模糊聚类算法的提出，主要是出于对4.1节所述的两类算法（IMMFC算法以及SPFCM算法）所存在问题的解决需要，是基于上述算法的改进与完善。上述两种算法的主要局限性在于中心点的选取要点。中心点的选择要点并非对于其个数的选取要求，而是对于其权重的选取要求。因此，对于大数据中数据挖掘模型的增量型模糊聚类方法的改进，主要是中心点选择上的改进。用户可以依据条件需要，设定固定比例[K1]，在整体数据当中选取的中心点的权重和与整体数据的权重和的比值为[K2]，将[K2]与[K1]进行比较，从而选出具有代表性的中心点，做出最优聚类方案。这样做的好处是比例值更为直观和精确地反映出所选中心点在整体数据当中的足够权重，使得其更具代表性。这也是提出以最小权重阈值为依据而改进的增量型模糊聚类方法。

4.2.2  算法的主要思路

增量型模糊聚类算法将规模很大的整体数据划分成多个小数据块，对于其中的任意个小数据块，都会对其通过增量型模糊类算法进行模糊聚类的操作。模糊聚类之后，能够得到相应的模糊隸属度矩阵以及权重矩阵，而后从权重矩阵当中选出能够作为集群代表的中心点。设计的算法主要以最小权重阈值为依据，同时取与IMMFC算法相同的目标函数。其思路如下：首先按照增量型模糊聚类算法的模式，将整体数据进行多个小数据块的合理划分，而后对每一个小数据块做出模糊聚类的处理，模糊聚类之后，每一个数据块中选取3个权重较大的数据作为一个中心点。此中心点既代表其中3个数据对象聚为一类的概率相对较大，同时作为中心点参与最后的算法运算。全部的小数据块模糊聚类完成之后，依照选取的中心点的权重与整体数据权重的比值[K2]，确定中心点选取的最小权重阈值，从而确定中心点选取个数。所选取的中心点集合组成新的数据块，对此数据块进行模糊聚类，得到最终权重矩阵，任意集群中的中心点选取该集群中权重最大者，同时，按照集群中所有数据到此中心点距离进行分类。

4.3  以最小权重阈值为依据的增量型模糊聚类算法的实现

依据4.2.2节中算法的主要思路，对算法进行设计并得以实现。算法中整体数据的小数据块划分完成之后，对其隶属度矩阵[U]以及权重矩阵[V]进行计算。以所给定的最小权重阈值作为基础依据，将前[m]个数据的权重选入，数量[m]依据各数据的权重和接近最小权重阈值的程度来确定。而后得到集群中3个权重相对最大的数据组成中心点[A]，此中心点[A]与其他中心点组成新的数据块，求得最后中心点之后，以此中心点对集群中所有数据进行分类。

确定算法之前，可对所设计算法中相关参数做出如下定义：整体数据有[n]个数据对象，被分成[m]个集群，其中，[dab]是数据对象[a]到数据对象[b]之间的欧几里得空间距离，[Uca]是对象[a]到集群[c]的模糊隶属度，[μbc]是对象[b]到集群[c]的权重。同时，定义[Nn， Nv]以及[Su]三个参数，其中，[Nn， Nv]负责进行阈值权重的调节，[Su]负责相关权重的调节。通过拉格朗日乘数法对权重矩阵[V]和隶属度矩阵[U]进行推导，得到其更新公式如下：

模糊隶属度的公式可用类似方法算出，此处不再赘述。

详细的算法流程如下：

算法1：隶属度矩阵的初始化

输入：集群数量[m]，距离矩阵[Q]

输出：完成初始化后的隶属度矩阵[Um×n]

1. 确定空集[N]为初始化集合

2. 整体集群中所有數据中距离最小的数据[q]作为首个中心点，纳入集合[N]。同时，定义变量[j=1]，[Ujq=1， Uja=0]，其中，[a]=1，2，…，[p-1]，[p+1]，…，[n]。

3. 令[m=m+1]，而后在所有最小距离中选择数据最大者[q]定为中心点，纳入集合[N]。

4. 定义变量[Ujq=1， Uja=0]，其中，[a]=1，2，…，[p]?1，[p+1]，…，[n]。

5. 集合[N]中个数与集群数量[m]作比较，当二者相等时结束算法。

算法1流程图如图6所示。

算法2：权重矩阵的计算以及隶属度矩阵算法的计算

输入：集群数量[m]，距离矩阵[Q]，参数[Nn， Nv]以及[Su]，停止阈值[z]

输出：隶属度矩阵[U]，权重矩阵[V]

1.通过算法1对隶属度矩阵[U0]进行初始化，确定迭代序号[h=0]。

2.令[h=h+1]。

3.通过公式计算对权重矩阵以及隶属度矩阵进行更新。

4.将[Uh-Uh-1]与停止阈值[z]相比，直到其值小于停止阈值[z]，结束。

算法2流程图如图7所示。

算法3：以最小权重阈值为依据的增量型模糊聚类算法

输入：集群数量[m]，最小权重阈值[r]，停止阈值[z]，相关参数[Nn， Nv]以及[Su]，[s]个距离矩阵的数据块[Rpnp×np]。

输出：权重矩阵[Vp]及隶属度矩阵[Up]。

1.定义空集[E]为中心点集合，空集[F]为每个数据块中3个权重最大的数据组成的中心点集合。

2.通过算法2对数据块进行处理，求得权重矩阵[Vp]以及隶属度矩阵[Up]。

3.依据最小权重阈值[r]，确定加入集合[E]的最少的中心点数量。

4.每个数据块中选择3个权重最大的数据组成中心点，纳入空集[F]。

5.依次处理数据块，直到数据块处理完成后执行下一步。

6.通过集合[E]的距离矩阵以及集合[F]，通过算法2获得最后的权重矩阵[VP]以及隶属度矩阵[Up]。

7.结束

算法3流程图如图8所示。

4.4  对算法的实验测试

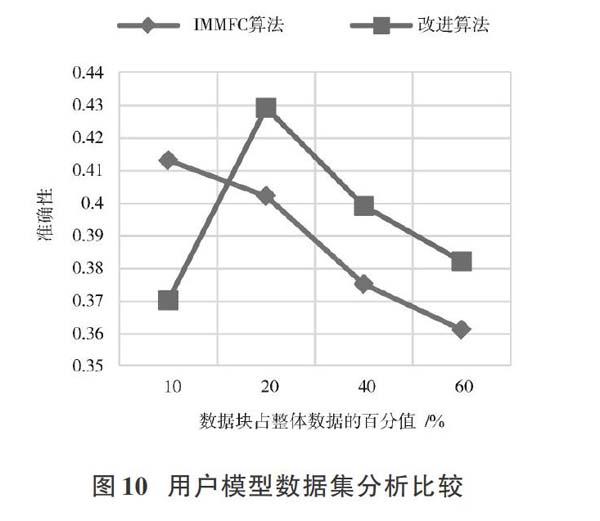
实验通过对采集到的水稻数据集以及用户模型的数据集的分析，将改进后的以最小权重阈值为依据的增量型模糊聚类算法与IMMFC算法相比较。其中，实验参数[Nu]取值为0.1，最小权重阈值[r]为1.5，停止阈值[z]为[1×10-5]，水稻数据集聚类数[k]取2，用户模型数据集聚类数[k]取3，参数[Nn， Su]遵照IMMFC算法的相关规则。实验数据的分块划分依据依次是数据块占整体数据的10%，20%，40%，60%。实验的精确性结果如图9，图10所示。

由图9，图10分析易得，整体来看，改进算法进行聚类的准确性在高于10%的情况下均高于IMMFC算法。

5  结  论

大数据中数据挖掘模型的算法决定了数据挖掘过程当中的精确性和高效性[7]。传统的模糊聚类算法以及增量型模糊聚类算法虽然能够较好地助力数据挖掘，但是普适性仍然不强。实验证明，以最小权重阈值为依据的增量型模糊聚类能够在很大程度上克服这一问题，为大数据中的数据挖掘带来便利。

参考文献

[1] MACQUEEN J. Some methods for classification and analysis of multivariate observations [C]// Proc of Berkeley Symposium on Mathematical Statistics & Probability. Berkeley， Calif.： University of California Press， 1965： 281?297.

[2] KAUFMAN L， ROUSSEEUW P J. Finding groups in data： an introduction to cluster analysis [M]. Hoboken， New Jersey： John Wiley & Sons， Inc.， 1990.

[3] 谢娟英，屈亚楠.密度峰值优化初始中心的K?medoids聚类算法[J].计算机科学与探索，2016，10（2）：230?247.

[4] 许凯，吴小俊，尹贺峰.基于分布式低秩表示的子空间聚类算法[J].计算机研究与发展，2016，53（7）：1605?1611.

[5] 郑超，徐恬.一种改进的核模糊聚类算法[J].软件导刊，2016，15（1）：41?42.

[6] 李滔，王士同.适合大规模数据集的增量式模糊聚类算法[J].智能系统学报，2016，11（2）：188?199.

[7] 郑和荣，陈恳，潘翔.结合代表点和密度峰的增量动态聚类算法[J].浙江工业大学学报，2017，45（4）：427?433.

[8] 惠飞，黄士坦.基于灰度特征聚类的图像自动分割方法[J].武汉大学学报，2009，43（6）：405?408.

[9] 刘硕，胡雅婷，马驷良.基于模拟退火的无监督和模糊聚类算法[J].吉林大学学报，2009，47（2）：317?322.

[10] GRAVES D， PEDRYCZ W. Kernel?based fuzzy clustering and fuzzy clustering： a comparative experimental study [J]. Fuzzy sets and systems， 2010， 161： 522?543.