基于划分的数据挖掘K?means聚类算法分析

曾俊

摘  要： 为提升数据挖掘中聚类分析的效果，在分析数据挖掘、聚类分析、传统K?means算法的基础上，提出一种改进的K?means算法。首先将整体数据集分为[k]类，然后设定一个密度参数为[?]，该密度参数反映数据库中数据所处区域的密度大小，[?]值与密度大小成正比，通过密度参数优化[k]个样本数据的聚类中心点选取;依据欧几里得距离公式对未选取的其他数据到各个聚类中心之间的距离进行计算，同时以此距离为判别标准，对各个数据进行种类划分，从而得到初始的聚类分布;初始聚类分布得到之后，对每一个分布簇进行再一次的中心点计算，并判断与之前所取中心点是否相同，直到其聚类收敛达到最优效果。最后通过葡萄酒数据集对改进算法进行验证分析，改进算法比传统K?means算法的聚类效果更优，能够更好地在数据挖掘当中进行聚类。

关键词： 数据挖掘; 聚类分析; K?means聚类算法; 聚类中心选取; K?means算法改进; 初始中心点

中图分类号： TN911.1?34                       文献标识码： A                          文章编号： 1004?373X（2020）03?0014?04

Analysis of partition?based data mining K?means clustering algorithm

ZENG Jun

（College of Big Data and Intelligent Engineering， Yangtze Normal University， Chongqing 408100， China）

Abstract： An improved K?means algorithm on the basis of the analysis of data mining， clustering analysis and traditional K?means algorithm is proposed to improve the effect of clustering analysis in data mining. The whole data set is divided into [k] classes firstly， and then a density parameter [?] is set， which reflects the density of the area in which the data is located in the database. The value of [?] is proportional to the density. The selection of cluster center points of [k] sample data is optimized by the density parameter. The distance between other unselected data and each cluster center is calculated by Euclidean distance formula. At the same time， the distance is taken as the criterion to divide each data into different categories， so as to get the initial clustering distribution. After the initial clustering distribution is obtained， the center point of each distribution cluster is calculated again to judge whether it is the same as the previous center point， until the clustering convergence reaches the optimal effect. Finally， the wine algorithm is used to verify and analyze the improved algorithm. The results show that the improved algorithm has better clustering effect than the traditional K?means algorithm， and can better perform clustering in data mining.

Keywords： data mining; clustering analysis; K?means clustering algorithm; clustering center selection; K?means algorithm improvement; initial center point

0  引  言

信息时代的来临及其快速发展为人们的生活与工作带来了极大便利，数据资源对于人们的影响也越来越大。如何从庞大繁杂的数据资源当中汲取有效信息变得极其重要，数据挖掘应用而生。聚类分析在数据挖掘模型当中的作用巨大。基于划分的K?means算法是聚类分析中具有代表性的算法，其收敛性相对较强，但传统的K?means仍存在诸多问题，对于K?means算法应当如何改进，怎样通过算法融合和各类技术手段进行优化，很多专家学者对此相当关注。当前K?means算法主要存在的缺陷主要是样本数据[k]值的选择，孤立点的影响仍然难以消除等。同时，K?means算法计算量相对较大，需要承担较大的计算压力。本文提出通过设定密度参数进行初始中心点的优化，从而进行聚类分析，做到更好的数据挖掘效果。

1  数据挖掘概述

1.1  数据挖掘的现状

总体来看，数据挖掘所要研究的数据大致可以分为半结构化数据、结构化数据、非结构化数据以及异构数据等[1]。

随着信息技术翻天覆地的发展与进步，数据挖掘以及人工智能在生产生活当中的位置愈发重要。无论是工业生产还是日常生活，都能够通过数据挖掘带来更好的利益与便利，更好地提高人民的生产生活水平。

1.2  数据挖掘的流程

数据挖掘的一般流程如下简述：

1） 对数据进行选择以及集成，是指从已有的数据库当中进行相应的目标数据选取，并以此作为下一步的处理目标。

2） 对所选数据进行预处理，是指对所选数据当中的重复部分以及噪声做出消除，同时对缺失数据进行计算弥补。数据的预处理是整个数据挖掘过程当中的关键一步，其中步骤不需要顺序排列，同时可以多次执行以达到所求效果。

3） 数据的转化，数据转化的过程是将步骤2）所得数据进行对应实际需求的转化，如多维到低维的转化，通过转化达到数据挖掘更为高效的目的。

4） 相关数据挖掘的算法，依据聚类、回归、概括或者分类等各种模型的建立，做出对应的数据建模。

5） 对数据做出进一步的评估，以获得有价值的结论，提供实用信息。

2  聚类分析简述

2.1  聚类分析的定义

聚类分析是指对整体的数据库依据一定算法进行分析与计算，将其进行类别划分，同类当中的数据具备尽量大的相似性，不同类之间的差异性尽可能大[2]。具体表达上，整体数据可以定义为集合[N]，[N=x1，x2，…，xn]，其中，[n]表示整体数据中的数据量。在对整体数据库[N]进行聚类时，把数据库[N]中的[n]个数据依照目标相似度进行划分，划分为[m]类[y1，y2，…，ym]，其中，[yi]为划分的第[i]类，聚类结果用集合[Q]表示，表达式如下：

2.2  聚类分析的现状

聚类分析目前已经应用到各类领域，其中难点是算法的普适性以及有效性的提升[3]。这主要是由于当前信息时代越来越大的数据分析需求。同时，聚类分析作为以距离为主要分析依据的划分技术，理论依据是统计学与机器学习。当前聚类分析的发展中，由于需要面对越来越庞杂的数据量，聚类分析往往存在一定缺陷，难以实现高效和精准。大数据时代数据的差异性也决定了很难找到一个普适的聚类算法对所有数据进行分析。

多数聚类算法与爬山算法有一定的相同之处，其缺点主要表现在两个方面：一是容易产生局部最优;二是数据量过大时，往往难以聚类精准。因此，聚类算法仍然需要不断的完善与改进，以适应更大更复杂的数据处理。具体上，可以通过学科互补进行聚类分析的优化。如以混沌理论作为基本依据的聚类分析或者是借助各类优化算法所进行的聚类分析[4]。

2.3  聚类分析的流程

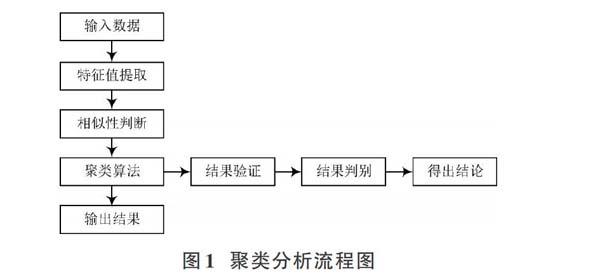
聚类分析旨在理清整体数据，首要工作是整体数据的选择，并从中进行信息提取。在此过程中，欧几里得空间距离是其相似性的基本判断依据。相似性判断之后，进行对应的结果验证[5]。通常结果验证需要进行多组数据的检验，以提高其普适性。聚类分析具体的流程如图1所示。

2.4  聚类算法的数据结构

聚类算法的数据结构主要分为两类：一类是相异度矩阵;另一类是数据矩阵。下面对两类数据结构做简单介绍。

2.4.1  相异度矩阵

相异度矩阵主要体现样本数据之间的差异性，其作为对象?对象的一种数据表达方式，是多种聚类算法的底层基础。当样本数据为[m]时，其相异度矩阵为[m×m]维，所表达的是[m]个样本数据的差异性。对于含[m]个样本数据的数据库集合[N=a1，a2，…，an]来说，其相异度矩阵可以表示为：

式中[d（i，j）]是样本数据[i]与样本数据[j]之间的量化表示，多数情况下，此值非负。若两个样本数据之间的相似度越高，则此值相应越小;若两个样本数据之间的相异度越高，则此值越大。

2.4.2  数据矩阵

数据矩阵能够对整体数据当中的所有样本数据的属性值进行表示。其数据样本以行表示，数据的属性以列表示。如数据库所组成的集合[Q=a1，a2，…，an]，其对应的数据对象[ai]若有[m]个属性，则表示其维度为[m]，矩阵表示如下：

3  K?means聚类算法简述

3.1  K?means算法研究现状

K?means聚类算法自提出至今，有关于此类算法的研究有很多。同时在工商业、科学、统计学以及人工智能等各个领域有广泛的应用。当下比较热门的微博热点的提取、银行中客户信息的整理以及图形处理等方面都会应用到K?means聚类算法。近年来，关于K?means算法的优化算法多种多样，同时学者们也对K?means算法做出了进一步的完善，如通过聚类评价指标的更新获得更好的聚类结果;利用學科融合，K?means算法与粒子群相结合或是K?means算法与神经网络相结合的算法等[6]。

3.2  K?means算法的基本思想与实现步骤

K?means算法是基于划分的一类经典的聚类算法，此类算法能够在[n]维的数据空间中进行广泛应用。K?means算法通过多次迭代对给定的样本数据进行不同的种类划分，划分的每一种类的内部数据尽可能相似，与其他种类的数据尽可能相异。K?means算法的基本思想是：首先将整体数据集分为[k]类，并从整体数据集当中选取[k]个样本数据作为最初的聚类中心;最初聚类中心确定之后，依据欧几里得距离公式对未选取的其他数据到各个聚类中心之间的距离进行计算，同时以此距离为判别标准，对各个数据进行种类划分，从而得到初始的聚类分布。初始聚类分布得到之后，对每一个分布簇进行再一次的中心点计算，并判断与之前所取中心点是否相同，若不同，则进行新的迭代调整，直到其聚类收敛能够达到研究所需，停止迭代，结束算法。K?means聚类算法进行聚类的过程是通过迭代计算对中心点进行更好确立的过程。此类算法往往简便易行、效率较高，同时收敛速度很快。其具体步骤简述如下：

1） 设整体数据集为[N]，在数据集[N]中选择[k]个样本数据，这[k]个样本数据定义为最初聚类中心，得到[M1]，[M2]，…，[Mk]个最初的聚类中心点，以此区别划分种类的数量。

2） 对数据集合中未选取的样本数据到各个聚类中心点间的距离进行计算，并依据距离进行样本数据的划分，形成初始的聚类分布。

3） 以公式[Mi=1nix∈φiN]为计算依据，对各个聚类簇进行再一次的中心点计算，所得到的新的中心点用[Mn1，Mn2]，…，[Mnk]表示。

4） 判断是否符合目标收敛度，若不符合，则返回步骤2），直到满足目标收敛度为止。

5） 输出所得的聚类数据。

K?means算法的流程图如图2所示。

4  优化中心点对K?means算法进行改进

4.1  提出问题

K?means算法是否能够产生更好的聚类效果，在很大程度上取决于初始中心点的选取。原有的K?means算法在进行初始中心点选取时，无法确定中心点选取是否整体分散，抑或中心点是否会选择到噪声数据或者是边缘数据。其聚类结果的时效性以及稳定性无法得到保障。具体应用当中，找到合适的中心点能够帮助K?means算法达到效果最优。

K?means算法的中心点选取时，受数据分布影响会产生较大误差，可参照图3进行分析。

图3中，a）与b）中心点与其中部分对象的欧氏距离相同，但是二者的整体分布存在差异;b）与c）的整体分布大致相同，但是个别点与中心点的距离不同。在中心点的选取过程当中，个别中心点选取所反映的整体数据分布存在差异。如何选取一个合适的中心点，更好地处理整体数据分布，反映数据聚类信息，是解决中心点选取的关键。

4.2  通过密度参数优化中心点选取

可以设定一个密度参数为[?]，该密度参数反映数据库中数据所处区域的密度大小，[?]值与密度大小成正比。此值通过以选定的样本数据[ai]作为中心，将与其距离相近的[n]个参数到此对象的距离平均值作为[?]值。主要的算法依据是：首先通过欧几里得空间距离进行样本数据之间的距离计算;而后对各数据的密度参数[?]值进行计算，并计算[?]值的平均值[?]。所有密度参数值组成集合[D]。[k]个初始中心点从集合[D]中进行选取，而后进行基于K?means算法的聚类分析。从集合[D]中选取[k]个初始中心点的步骤如下：

1） 在密度集合[D]中选择最小密度参数值[?]所对应的样本数据，以此作为首个聚类中心点[ai（i=1）]。

2） 集合[D]删除[?]半径内的数据与中心点[a1]。

3） 令新的密度集合为[D]，并计算密度参数[?]。

4） 执行步骤1），得到聚类中心点[ai]。

5） 判断[i]是否等于[k]，若是，则输出[k]个中心点。否则，返回步骤2）。

中心点选取的具体流程如图4所示。

中心点选取完毕后，依照K?means算法的步骤进行聚类分析。

4.3  结果验证与分析

通过Wine葡萄酒数据集对改进算法进行验证分析。Wine葡萄酒数据集包括3种起源不同的葡萄酒的178条记录。同时，包含13个不同属性，表示葡萄酒的13种不同化学成分。实验采用传统K?means算法改进后的算法相对比的方式进行，并得出对应的实验结果。实验结果如表1所示。

通过实验结果不难发现，K?means算法的聚类结果不够稳定，其准确度多数低于改进算法。同时，K?means算法的准确度均值要低于改进算法。实验结果证明，改进算法比K?means算法的聚类效果更优，能够更好在数据挖掘当中进行聚类分析。

5  结  语

针对传统K?means算法中心点选取的不足之处，借助密度参数对中心点选取进行优化。经过实验对比分析，改进算法比传统K?means算法的聚类效果更优，能够更好地在数据挖掘当中进行聚类。

参考文献

[1] 李国杰，程学旗.大数据的研究现状与科学思考[J].中国科学院院刊，2012，27（6）：647?657.

[2] 黄敏，何中市.一种新的K?means聚类中心选取算法[J].计算机工程与应用，2011，47（35）：132?134.

[3] 刘兵，夏世雄，周勇.基于样本加权的可能性模糊聚类算法[J].电子学报，2012，34（5）：1332?1335.

[4] 郑丹，王潜平.K?means初始聚类中心的选择算法[J].计算机应用，2012，32（8）：2186?2188.

[5] 金晓民，张丽萍.基于最小生成树的多层次K?means聚类算法及其在数据挖掘中的应用[J].吉林大学学报（理学版），2018，56（5）：153?158.

[6] 龚敏，邓珍荣，黄文明.基于用户聚类与Slope One填充的协同推荐算法[J].计算机工程与应用，2018，54（22）：144?148.

[7] WANG Zhiqiong， XIN Junchang， YANG Hongxu. Distributed and weighted extreme learning machine for imbalanced big data learning [J]. Tsinghua science and technology， 2017（2）： 160?173.

[8] LI Peng， LUO Hong， SUN Yan. Similarity search algorithm over data supply chain based on key points [J]. Tsinghua science and technology， 2017（2）： 174?184.

[9] DAN Tao， LIN Zhaowen， WANG Bingxu. Load feedback?based resource scheduling and dynamic migration?based data locality for virtual Hadoop clusters in OpenStack?based clouds [J]. Tsinghua science and technology， 2017（2）： 149?159.