基于深度残差网络的医学图像鲁棒可逆水印算法

李 智，周旭阳，殷昕旺，张 丽(1.贵州省智能医学影像分析与精确诊断重点实验室，贵州 贵阳 550025; 2.贵州大学 计算机科学与技术学院，贵州 贵阳 550025)

随着网络技术的快速发展，智能医学和远程诊断技术日趋成熟。大量医学图像经常在网络上进行传输和使用，未授权者可轻易通过网络获取、存储、使用和篡改网络上的医学图像[1]。因而，保护医学图像的版权信息显得十分重要。数字水印算法是一种常用的信息隐藏技术，可用于医学图像的版权保护[2]。

在对医学图像进行保护时，为了不影响医生的诊断，不可破坏原始医学图像的信息，因此，基于医学图像的可逆水印算法成为研究者们关注的重点。郑洪英等[3]提出了基于位平面的可逆信息隐藏算法。首先，将医学图像分解为八位平面，通过压缩最高的四位平面获得对空间进行像素填充后的重建图像；其次，分别对重建图像的头部、中间、尾部进行加密；再次，利用直方图移位的方法将水印信息嵌入图像中。DENG等[4]针对医学图像的分区域典型特征，提出一种基于直方图平移的高容量无损信息隐藏水印算法。利用最大类间距方法确定前景区域和背景区域，通过使用聚合多边形和图像拟合算法确定前景嵌入区域，最终在前景和背景区域分别嵌入不同的水印。李智等[5]提出基于实质区域的精确分割算法获取医学图像中的实质区域为嵌入区域，以及基于隶属度的不规则实质区域拟合方法，并将多比特的基于编码的直方图平移(Code based Histogram Shifting, CHS)算法应用于整数小波变换中高频子带, 实现可逆水印嵌入。同时，使用增强奇异值分解在整数小波变换低频子带构建零水印, 实现医学图像的版权保护和篡改定位。现有的医学图像可逆水印算法大多在无损环境中运行，即载体在嵌入信息后不能受到任何攻击和修改。而在现实场景中，时常出现诸如图像压缩和几何变换等图像操作和攻击[6-7]。

在图像水印算法的研究中，通常是利用人工设定水印的嵌入强度参数，但是人工设定的参数具有较强的随机性，且得到的参数无法较好地均衡水印不可见性和鲁棒性[8]。水印的嵌入强度越大，则水印的鲁棒性越强，但不可见性越差; 水印嵌入强度越小，则水印的不可见性越好，但鲁棒性就越弱[9]。文献[10]对载体图像进行Contourlet变换后，对低频部分做块奇异值分解，其水印的主成分是通过修改块的最大奇异值的方式进行嵌入，虽然在数值上达到了不可见性的标准，但具有明显的块效应。文献[11]提出了一种基于奇异值分解和蜂群优化的鲁棒水印算法。嵌入强度的参数采用蜂群优化算法来选取，自适应均衡水印算法的鲁棒性与透明性，但蜂群优化算法收敛速度慢，寻找最优解时间较长。文献[12-13]基于群智能算法对水印嵌入强度进行优化，能够根据不同的图像确定最优的嵌入强度，但这些算法普遍不能较好地抵抗信号攻击。人类视觉系统(Human Visual System, HVS) 具有纹理掩蔽、频率掩蔽、亮度掩蔽等特性[14]。文献[15]基于HVS 特性确定图像掩蔽因子，并将其作为水印嵌入的强度，此类算法能降低载体图像的视觉失真，但算法较为复杂。ResNet是一种在图像处理领域应用的深度学习方法，它不仅可以提取图像的高维复杂特征，而且可以解决网络层数增多引起的精度退化问题，提升深度网络的性能[16-17]。

在平衡水印的不可见性和鲁棒性的同时，以上文献有一个共同特征为鲁棒性并不能满足需求。文献[18]在提取水印信息过程中引入K-means聚类方法，实现了水印区域的动态划分，但是初始聚类中心的选择对聚类结果影响很大，这就会造成水印算法性能不稳定。遗传模糊C-均值作为另一种聚类算法[19]，先应用遗传算法确定最优初始化聚类中心，再使用模糊C-均值(Fuzzy C-Means,FCM)方法得到最终的聚类结果，聚类结果不受聚类中心选择的影响，可解决水印算法性能不稳定的问题。

结合以上问题，本文提出一种基于ResNet的医学图像鲁棒可逆水印算法，利用改进的ResNet计算水印嵌入强度以平衡水印的不可见性和鲁棒性。在提取水印信息过程中，利用遗传模糊C-均值方法，有效提高了水印提取算法的鲁棒性。从嵌入和提取两个角度使基于医学图像的鲁棒可逆水印具有一定的实用性。

1 相关技术

1.1 残差学习

深度学习的基础网络从ALexNet(5个卷积层)、VGG(19个卷积层)到GoogLeNet(22个卷积层)，网络的结构在不断变深，更深的网络可以提取更复杂的特征[20-21]。但是，随着网络的加深，出现了训练集准确率下降的现象。HE等[22]提出ResNet，该网络结构可以避免简单堆叠的卷积神经网络梯度消失或爆炸以及精度退化问题，模型更容易优化，性能提升明显。

ResNet引入了残差学习，令x表示输入，H(x)表示残差单元的输出。一般情况下，卷积神经网络直接通过训练来学习H(x)，而残差学习则是使用多个含有参数的网络层来学习输入和输出之间的残差，F(x):=H(x)-x，那么残差单元的输出最终变为F(x)+x。实验证明，残差函数F(x)比H(x)更容易优化和学习。

一个完整的残差单元结构如图1所示。

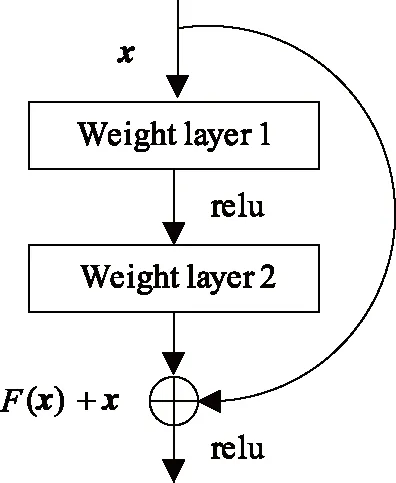
图1 残差学习单元Fig.1 Residual learning unit

在本文，残差单元定义为

y=F(x,{Wi})+x。

(1)

式中：x和y分别为残差单元的输入和输出；F(x,{Wi})为当前网络想要学习的残差函数。

定义：

F(x)=W2σ(W1x)。

(2)

式中：σ为 relu 激活函数，W1和W2分别为layer1和layer2的权重。为了简化表示，省略了偏差。

F(x)+x的操作是通过1个“跳跃连接”将对应元素进行相加来执行的。这种计算方式既没有引入额外的参数，也不增加计算复杂度，可解决层数增加之后出现的性能退化问题。式(1)中的输入向量x和函数F的维度应保持一致,否则，对输入向量x执行线性投影Ws来实现维度匹配，即

y=F(x,{Wi})+Wsx。

(3)

1.2 遗传模糊C-均值算法

FCM算法是一种有效的聚类算法。其基本思想：将n个样本数据N={n1,…,ni,…,nn}分为c类，并求得聚类中心V={v1,…,vj,…,vc}，N中任意样本ni对j类的隶属度为uij,分类结果可以表示为模糊隶属度矩阵U={u11,…,uij,…,unc}。FCM是通过最小化隶属度矩阵U和聚类中心V的目标函数JFCM(U,V) 来实现：

(4)

约束条件：

(5)

式中：参数m>1为模糊系数，用来控制隶属矩阵U的模糊程度，m越大越模糊，通常m=2是比较理想的取值；dij=‖ni-vj‖为ni到聚类中心vj之间的欧式距离，应用拉格朗日乘数法并结合约束条件，使目标函数JFCM(U,V)得到最小值的必要条件如式(6)(7)所示。对式(6)和(7)进行迭代运算，直至算法收敛。

(6)

(7)

FCM算法对初始聚类中心敏感，容易收敛于局部最优解。遗传算法(Genetic Algorithm, GA)具有领域无关的群体性全局搜索能力, 将遗传算法与模糊聚类算法进行组合，可以有效地解决FCM算法局部寻优的缺点。由遗传算法生成最优初始聚类中心，再使用FCM 算法得到最终的分类结果。遗传FCM算法的处理流程如图2所示。

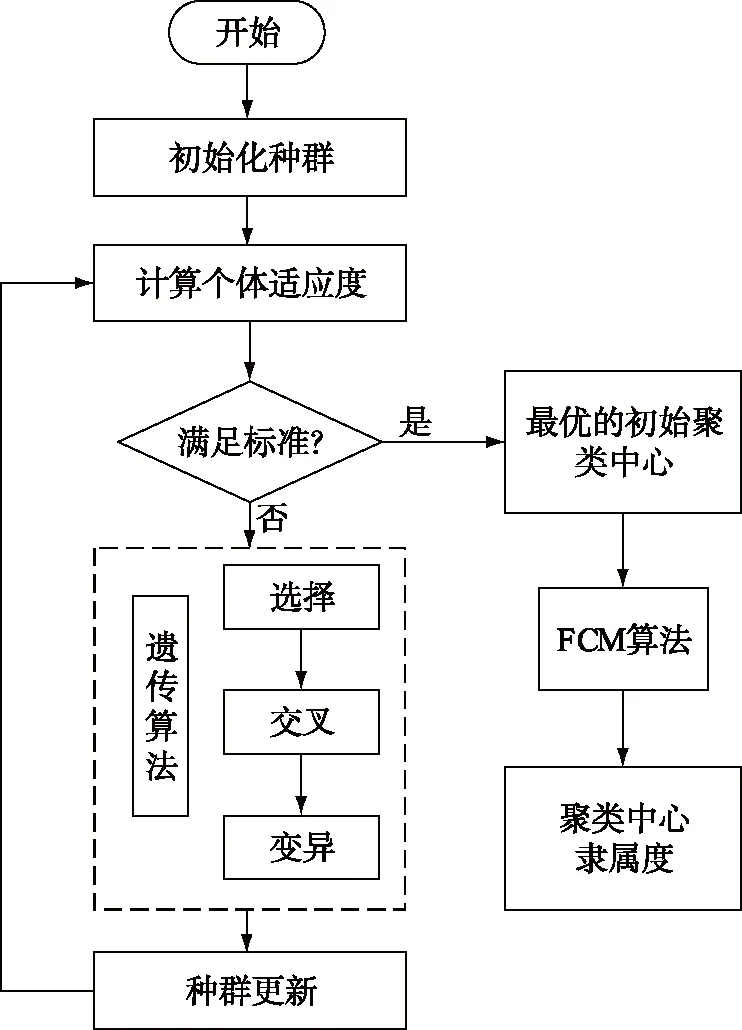
图2 遗传模糊C-均值流程图Fig.2 Flow chart of genetic fuzzy C-mean

2 算法实现

2.1 深度残差网络模型

在现有算法中，大多是依靠经验手动设置嵌入强度，不仅没有理论依据，也很难获取最优嵌入强度平衡不可感知性和鲁棒性。为了实现不可感知性与鲁棒性的有效折衷，本文提出一种深度残差网络模型。它通过残差学习可以提高提取图像尺度、亮度、纹理等复杂特征的能力，更为精确地评估图像对噪声的局部敏感性，自适应获得水印嵌入强度λ。

此深度残差网络模型以医学图像作为输入，由医学图像对应的嵌入强度作为标签，学习医学图像和图像嵌入强度之间的映射关系。模型训练完成后，可以直接通过医学图像预测嵌入强度。由于医学图像的大小一般较大，为了提高网络的拟合速度和增加样本数量，医学图像被分成 32×32的图像块作为输入。

2.1.1网络结构

如图3所示，网络模型一共有19层，包括卷积层、残差单元、全局平均池化层和全连接层。网络输入大小为32×32的医学图像。首先，通过的1个卷积层(使用大小为3×3×16的卷积核)；其次，经过9个残差单元(分别使用大小为3×3×16、3×3×32、3×3×64的卷积核)，为了获取更多、更丰富的特征信息,卷积核的数目随着网络的深入不断增加；再次，网络以全局平均池化层和全连接层结束，输出大小为1×1的嵌入强度。网络通过步长为2的卷积层直接进行下采样。为了保持特征图的大小与输入一致,将步长和边缘填充都设置为 1。

残差单元由2个卷积层和1个“跳跃连接”组成，卷积层主要有大小为3×3的卷积核，并遵循2个简单的设计规则[22]：(i)当输入和输出特征图的大小相同时，该卷积层和上一层具有相同数量的卷积核；(ii)如果特征图的大小减半，则卷积核的数量加倍，以便保持每层的时间复杂度。在跳跃连接中，当输入和输出的维度是相同时，可以直接使用式(1)连接(如图3实曲线)；当维度增加一倍时，用式(3)中的线性投影匹配维数(如图3虚曲线)。线性投影通过卷积核大小为1×1、步长为2的卷积实现。

图3 深度残差网络结构Fig.3 Deep residual network structure

2.1.2网络训练

卷积神经网络的训练过程就是损失函数的最小化过程，本文的深度残差网络模型将预测嵌入强度和标签嵌入强度的均方误差作为损失函数：

(8)

式中：n为批处理量大小，W为权重参数集合，xi为批处理图像中第i幅医学图像，yi为相对应xi的嵌入强度，f(W,xi)为预测第i幅医学图像的嵌入强度。

本文采用随机梯度下降法最小化损失函数。在每个卷积之后和激活函数之前，我们采用批量归一化(Batch Normalization, BN)。BN 层有助于网络的收敛，批量大小设置为64，即在样本图像中随机选取 64个图像和与之对应的标签嵌入强度作为一个批量进行网络训练。网络一共训练了 200 epoch，学习率从0.1开始，当误差停滞时，将学习率除以10。

2.2 水印嵌入算法

步骤1预处理医学图像。医学图像I的大小为2M×

2N，深度为tbit。为了避免像素溢出的问题，实现算法的可逆性，在嵌入水印之前，对医学图像I的像素进行调整：

(9)

式中：I(i,j)为医学图像I在(i,j)处的像素值，I′(i,j)为调整后的像素值，i、j为像素坐标，且1≤i≤2M,1≤j≤2N；η是调整尺度，且η≥λ。

步骤2构造小波系数均值(Mean of Wavelet Coefficients, MWC)直方图。算法选择MWC直方图作为嵌入区域，有助于实现水印图像的不可感知性。利用整数小波变换(Integer Wavelet Transform, IWT)将预处理后的医学图像I′进行分解，然后选取小波子带中的低高频子带(LH)和高低频子带(HL)，将其互不重叠地分割成大小为h×w的子带块，计算每个子带块的MWC，并构造MWC直方图，定义：

(10)

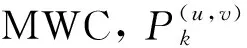
步骤3利用阈值约束选取感兴趣块。MWC 直方图服从零均值的类拉普拉斯分布，如图4所示。选取MWC直方图峰值及其邻域作为感兴趣块，用于嵌入水印信息。图中的阴影部分表示选取的感兴趣块。采用阈值约束选取感兴趣块SROI，定义：

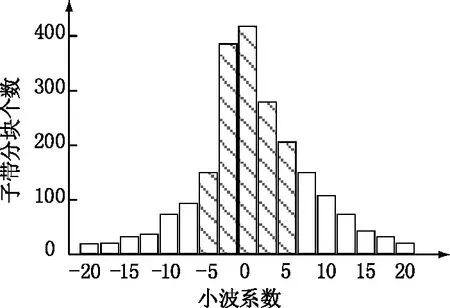
图4 MWC直方图Fig.4 MWC histogram

d(x,Sk)=|x-Sk|，

(11)

d(x,Sk)≤δ,1≤k≤n。

(12)

式中：d(·)为Euclidean距离函数，x∈{xl,xr}为MWC直方图的两个峰值点，δ为预先定义的阈值，并可以通过调整阈值δ来灵活控制水印容量。

步骤4基于深度残差网络计算水印嵌入强度λ。利用深度残差网络可以更好地提取医学图像尺度、亮度和纹理敏感度等复杂特征，训练医学图像和嵌入强度的关系模型，如图3所示。使用训练好的深度残差网络模型对医学图像进行计算得到嵌入强度λ。

步骤5水印嵌入模型。对步骤3所得的感兴趣块嵌入水印信息，嵌入过程定义：

(13)

(14)

(15)

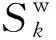
步骤6重构医学图像。对嵌入水印后的小波子带进行IWT重构，即可得到嵌入水印后的医学图像Iw。需要说明的是，边信息需要作为密钥传送到接收方，包括子带分块大小h×w、水印嵌入强度λ和调整的像素位置等。

2.3 水印提取算法

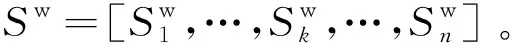
步骤2使用遗传模糊C-均值聚类算法对Sw聚类。设定聚类个数为3，类集合为class={classⅠ,classⅡ,classⅢ}，采用遗传模糊C-均值聚类算法对嵌入区域进行动态划分，嵌入区域划分的具体步骤：

:Sw=[Sw1,…,Swk,…,Swn],c=3,T=20:U,VGA():Step1 t=0,(N=50);Step2 ,f=1/JFCM,JFCM(4);Step3 ,[23];Step4 ,[23],pc=0.6;Step5 ,pm=0.2,,t=t+1;Step6 tT,,,Step2;FCM():Step7 FCM;Step8 (7)V;Step9 (6)U;Step10 (5),,,UV;Step8。

基于聚类结果，MWC 直方图被分成了三个区域，依次记为classⅠ，classⅡ 和classⅢ，如图5所示。

图5 嵌入水印图像MWC直方图Fig.5 MWC histogram of embedded watermark image

步骤3根据聚类结果提取水印信息。提取水印模型为

(16)

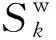
步骤4恢复感兴趣块。恢复公式为

(17)

步骤5复原医学图像Ir。恢复后的小波子带经过IWT重构之后，然后采用式(9)的逆操作来恢复嵌入过程中调整的像素，进而得到复原医学图像Ir。

3 实验结果分析

为了验证本文水印算法的高效性，首先，分析参数对性能的影响，为参数的优化选择提出建议；其次，给出了鲁棒性测试、可逆性测试、不可感知性测试的实验仿真结果；再次，分别与基于传统方法和基于深度学习方法的鲁棒可逆水印算法[18,24]进行性能对比。实验采用医学图像数据库(Medical Image Database, MID)的DICOM 样本图像集中的 300 幅磁共振成像(Magnetic Resonance Imaging, MRI)图像，本文选取大小为512×512的头、肺、腹腔、肝脏等不同部位的MRI图像作为载体，如图6所示。水印信息采用伪随机二进制序列。

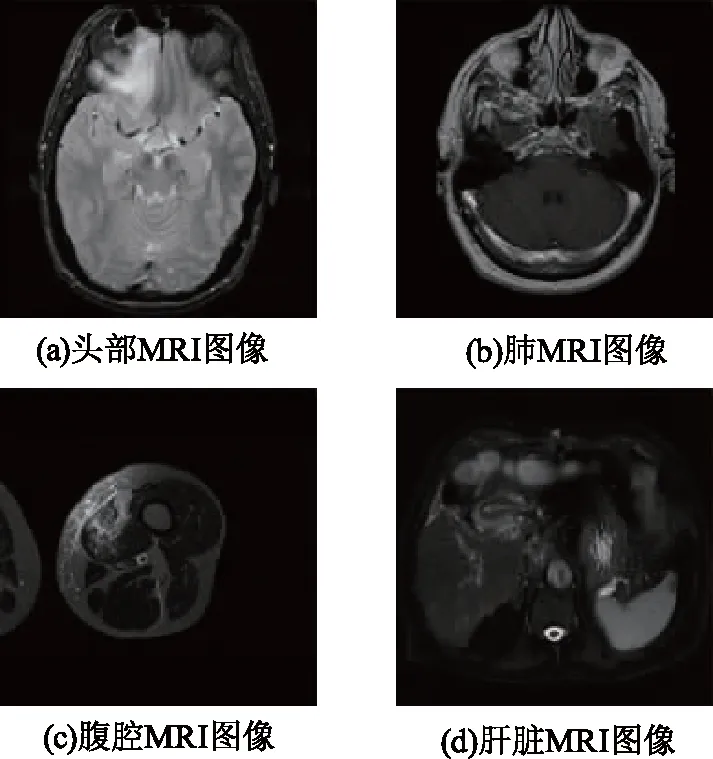
图6 测试图像Fig.6 Test image

3.1 性能评测指标

本文的关键问题是要同时实现水印算法的可逆性和鲁棒性，即：在无损环境下可以恢复宿主图像与水印，以及当受到攻击后可以正确恢复水印。一般来说，鲁棒可逆算法的评测指标主要包括：

(1)可逆性

图像错误率(Image Error Rate, IER)来评估可逆性，其值越低，表明算法的可逆性越好。定义：

(18)

式中：NErr_img为恢复图像错误的像素点数，Nimg为载体图像的总像素点数。

(2)不可感知性

不可感知性通常用宿主图像与水印图像间的峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)来衡量，定义：

(19)

式中：I(i,j)和Iw(i,j)分别为嵌入水印前后图像中(i,j)位置的像素值，2M×2N为图像大小。PSNR值越高，说明水印图像的视觉质量越好，隐秘信息越不容易被察觉，反之亦然。通常认为当PSNR值大于35 dB时，图像的差异通过肉眼已经无法进行判别。

(3)鲁棒性

在鲁棒性方面, 主要考虑应对高斯噪声(方差为0.01)、椒盐噪声(方差为0.005)、JPEG压缩(质量因子为25)和 JPEG 2000压缩。采用比特误差率(Bit Error Rate, BER)来衡量提取水印的正确性，定义：

(20)

式中：NErr为提取水印信息的错误比特数，Nbits为嵌入水印信息的总比特数。BER值越低，表明提取水印的正确性越高，水印抗攻击的鲁棒性越好。

(4)容量

容量反映在嵌入过程中宿主图像能嵌入的最大信息数量。一般在嵌入过程中，水印常常会和边信息一起进行嵌入，这时称宿主图像中实际嵌入的最大水印位数为纯容量。

3.2 参数分析

3.2.1嵌入强度

嵌入强度代表着嵌入水印的强弱，影响着可逆性、鲁棒性和不可感知性。本文实验选取小波子带中的低高频子带(LH)和高低频子带(HL)，子带分块大小为8×8，阈值为10，当嵌入强度选取5、10、15、20、25时，不同嵌入强度相对应的可逆性、鲁棒性和不可感知性测试如图7、8、9所示。由图可知，随着水印的嵌入强度越大，算法的鲁棒性和可逆性越来越强，但是不可感知性越来越差。

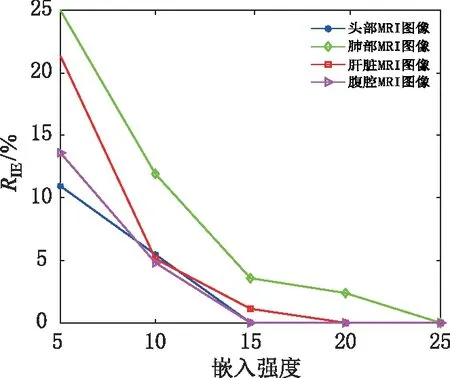
图7 嵌入强度和可逆性的关系Fig.7 Relationship between embedding strength and reversibility

3.2.2阈值

实验选取小波子带中的低高频子带(LH)和高低频子带(HL)，子带分块大小为8×8、嵌入强度为10，当阈值选取2、5、10时，相应嵌入水印信息后的MWC直方图如图10所示。由图可知，当阈值越小时，直方图聚类越明显，则可以更准确地提取水印信息。

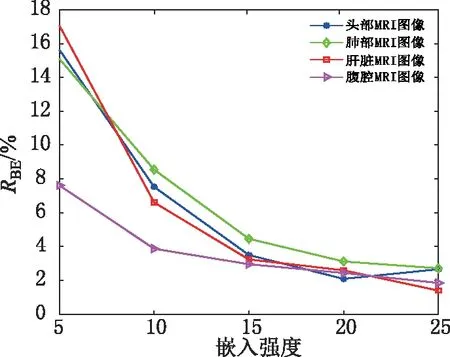
图8 不同嵌入强度下抗JPEG的鲁棒性Fig.8 Robustness against JPEG at different embedding strengths

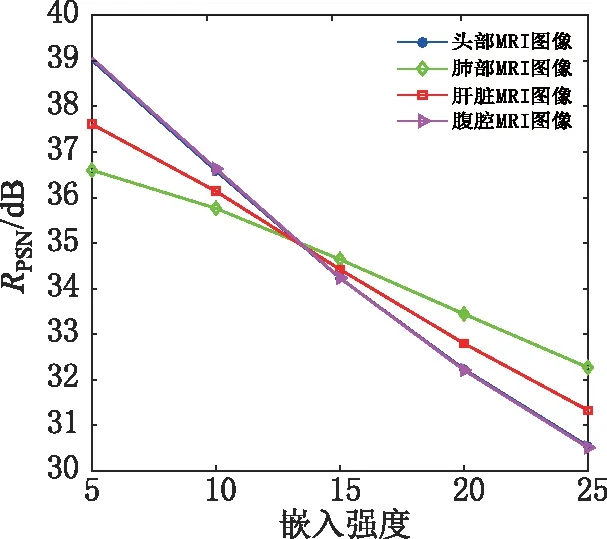
图9 嵌入强度和PSNR的关系Fig.9 Relationship between embedding strength and PSNR

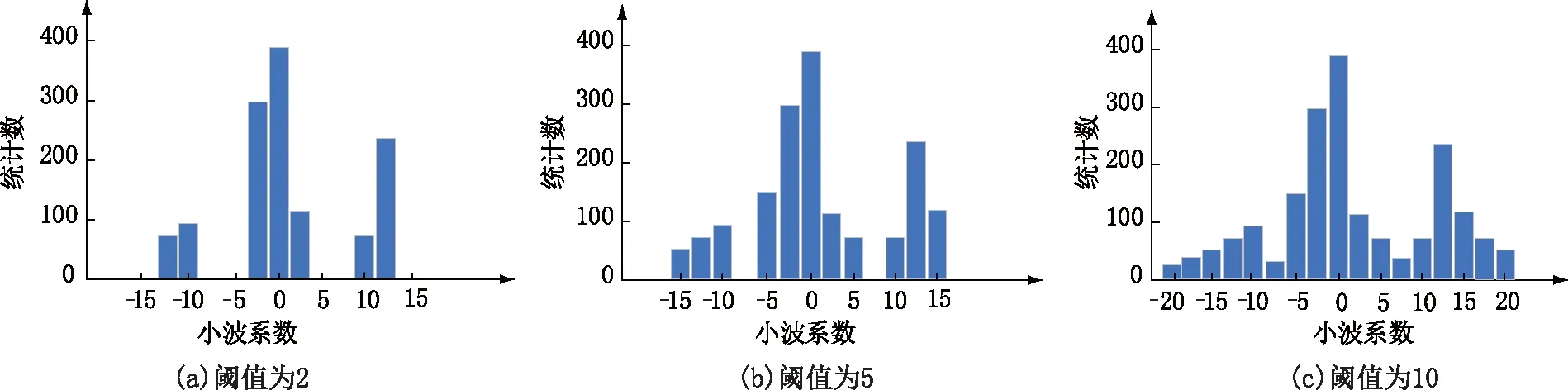
图10 MWC直方图Fig.10 MWC histogram

图11反映阈值选取2、5、10、15时，不同阈值下算法的鲁棒性。随着阈值的减小，算法的鲁棒性越好，反之亦然。根据多次实验得出，当阈值δ=λ/2时，算法有较好的鲁棒性，且可保证较大容量。

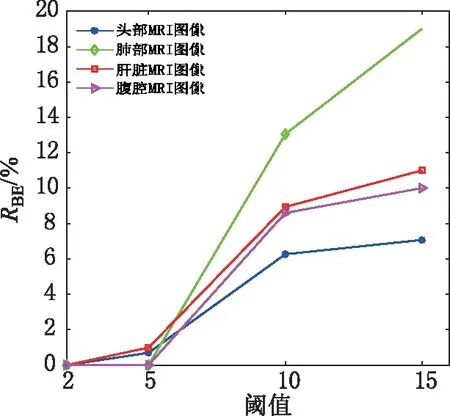
图11 阈值和鲁棒性的关系Fig.11 Relationship between threshold and robustness

3.2.3子带分块大小

子带分块大小也是影响容量、不可感知性和鲁棒性的重要因素。实验选取小波子带中的低高频子带(LH)和高低频子带(HL)、嵌入强度为10，当子带分块大小选取4×4、8×8、16×16、32×32时，研究子带分块大小对各性能的影响。

子带分块越大，子带分块个数越少，感兴趣块的个数就越少，水印嵌入容量随着块大小的增加而减少。由图12可以看出，随着块大小的减少，水印嵌入容量增加，反之亦然。由图13可以看出，随着子带分块大小的增加，PSNR 呈下降趋势。由图14可以看出，从整体上来说，随着子带分块大小的增加，抵抗攻击能力越强，鲁棒性呈增加趋势。

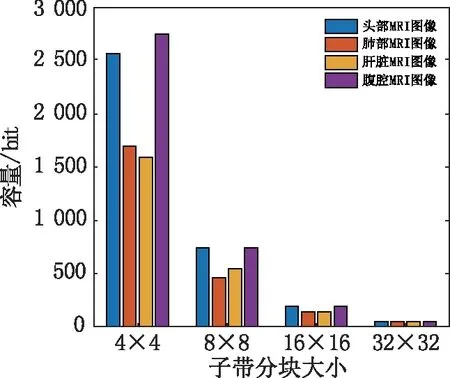
图12 子带分块大小和容量的关系Fig.12 Relationship between subband block size and capacity

图13 子带分块大小和PSNR的关系Fig.13 Relationship between subband block size and PSNR

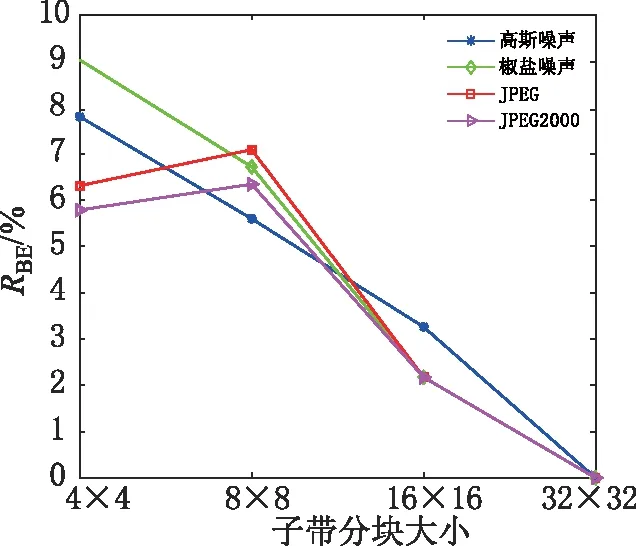
图14 子带分块大小和鲁棒性的关系Fig.14 Relationship between sub-band block size and robustness

3.3 实验仿真

为了验证本文算法的有效性，给出以不同部位医学图像为载体的水印嵌入和提取测试，实验结果如图15所示。图15中，(a1)、(b1)、(c1)、(d1)为原始图像，(a2)、(b2)、(c2)、(d2)为含水印的图像。从视觉效果来看，含水印图像与原始图像相比没有明显变化，具有良好的不可感知性；采用PSNR客观评价含水印图像与原始图像的质量差别，可以得出含水印图像的PSNR值分别为38.9、36.5、37.5、39.0 dB，都可以达到36 dB以上，图像的质量都表现良好。图15中，(a3)、(b3)、(c3)、(d3)为含水印图像与原始图像的差值图。可以明显看出水印嵌入前后的图像差别，以证明水印信息已嵌入载体图像。图15中，(a4)、(b4)、(c4)、(d4)为提取水印信息后的恢复图像，(a5)、(b5)、(c5)、(d5)为恢复图像与原始图像的差值图。差值图为全黑则表明恢复图像和原始图像完全一致，在没有受到攻击的情况下，算法没有更改原始图像的像素，IER值为0，说明本文算法实现了完全可逆的效果。

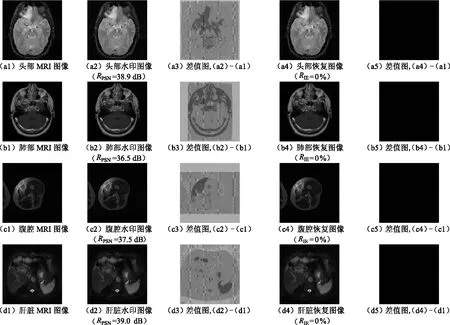
图15 实验结果Fig.15 Experimental results

为了检测本算法具有较好的鲁棒性，对含水印图像分别进行高斯噪声(方差为0.01)、椒盐噪声(方差为0.005)、JPEG压缩(质量因子为25)和 JPEG 2000压缩等常规攻击。表1列出了含水印图像在受到不同攻击后所提取水印的BER值。从表可以看出：攻击对提取出的水印 BER 值有一定的影响，但BER值都低于9%，特别是腹腔和肝脏受到压缩攻击时，提取出来的水印 BER 值大部分都能低于1%，说明本算法可以有效抵抗各种常规攻击，具有较强的鲁棒性。

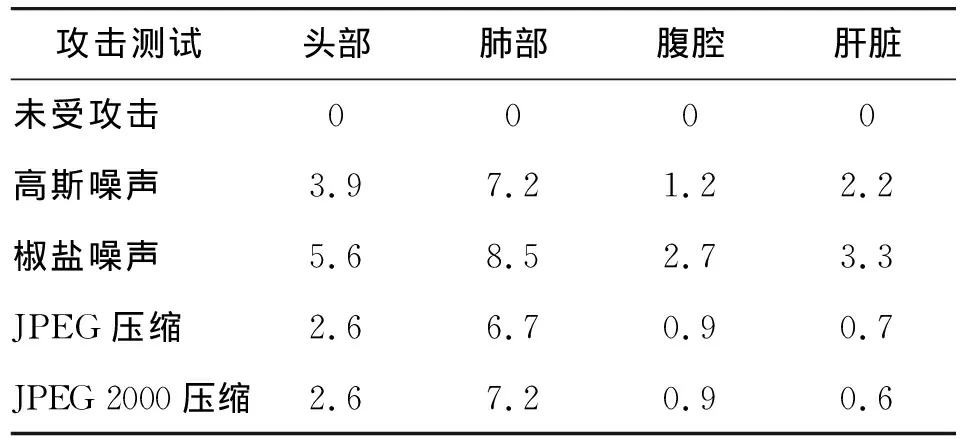
表1 鲁棒性测试Tab.1 Robustness test %

3.4 实验对比

为了进一步说明本文算法的优越性，从可逆性、不可感知性、鲁棒性和容量4个方面与文献[18][24]进行性能对比。文献[18]是基于聚类和小波变换的鲁棒可逆水印算法，文献[24]是基于卷积神经网络的鲁棒可逆水印算法。

(1)可逆性对比

我们采用 IER 来评估不同算法的可逆性，它在无损环境下衡量是否能实现图像与水印的无失真恢复。实验结果如表2所示，前2种算法接近实现可逆，相比之下，本文算法可以完全实现可逆效果。

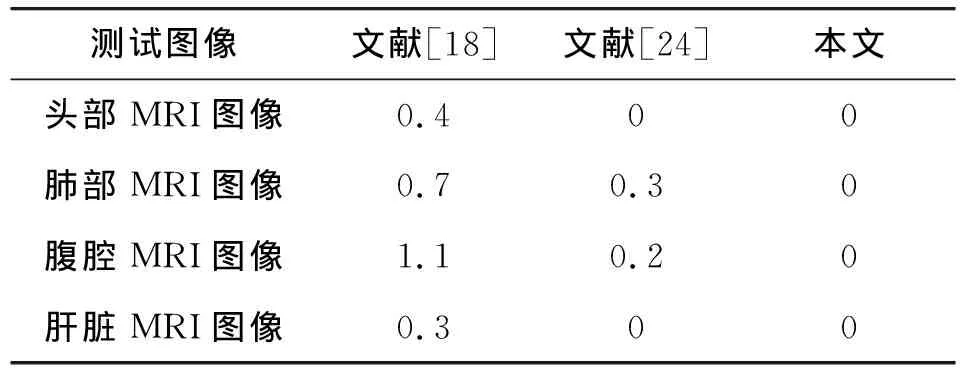
表2 可逆性对比Tab.2 Comparison of reversibility %

(2)不可感知性对比

不可感知性是对水印图像的失真情况进行评估，表3对比了不同算法的PSNR值。可以看出，本文的算法的PSNR值高达39.0 dB，图像质量要好于文献[18]和文献[24]。

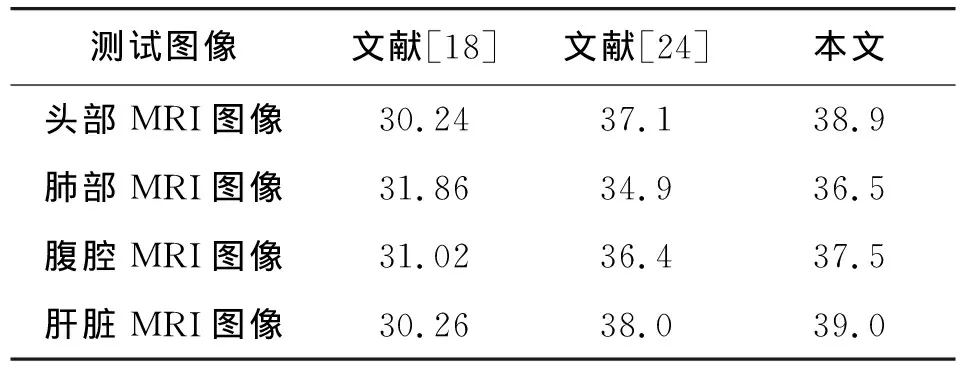
表3 不可感知性对比Tab.3 Comparison of imperceptibility dB

(3)鲁棒性对比

本文用BER对不同算法进行鲁棒性对比，表4—表7显示了实验结果。可以看出：文献[18]抗椒盐噪声和高斯噪声的鲁棒性比较差, 本文算法要优于所对比的方法,尤其在抗JPEG压缩和JPEG2000压缩时，肝脏图像的错误率可以低至0.7%和0.6%。

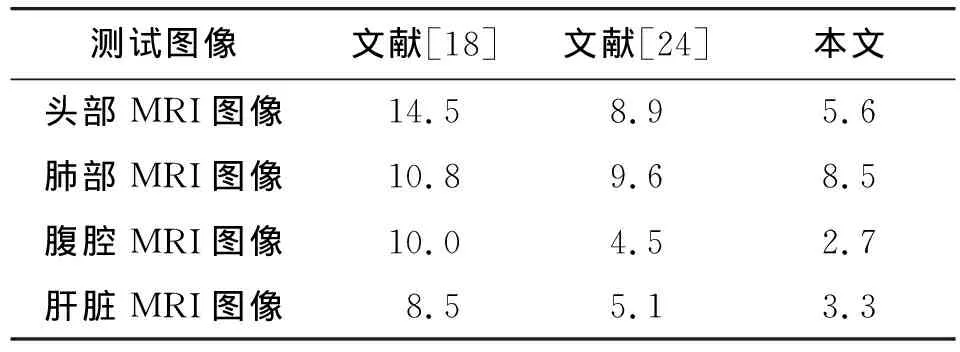
表4 鲁棒性对比-椒盐噪声(方差=0.005)Tab.4 Robustness comparison-salt and pepper noise (variance=0.005) %

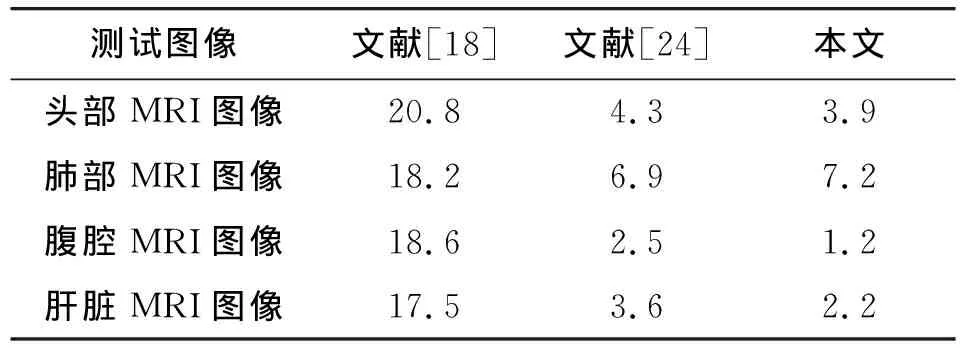
表5 鲁棒性对比-高斯噪声(方差=0.01)Tab.5 Robustness comparison-Gaussian noise (variance=0.01) %

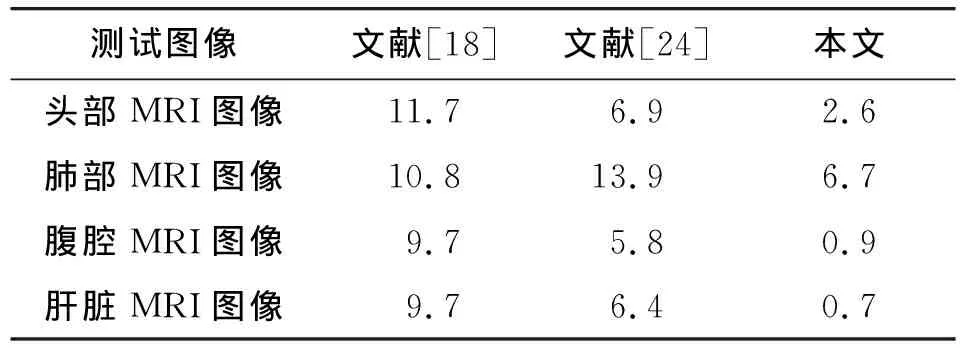
表6 鲁棒性对比-JPEG压缩(质量因子=25)Tab.6 Robustness comparison-JPEG compression (quality factor=25) %

表7 鲁棒性对比-JPEG2000压缩Tab.7 Robustness comparison-JPEG2000 compression %

(4)容量对比

表8对比了不同算法的容量，算法中设置块大小为8×8。本文算法的容量略高于文献[24]，明显高于文献[18]。因为本文算法选取了2个小波子带嵌入水印信息，而文献[18]只使用了1个小波子带，所以本文算法容量近似文献[18]的2倍。

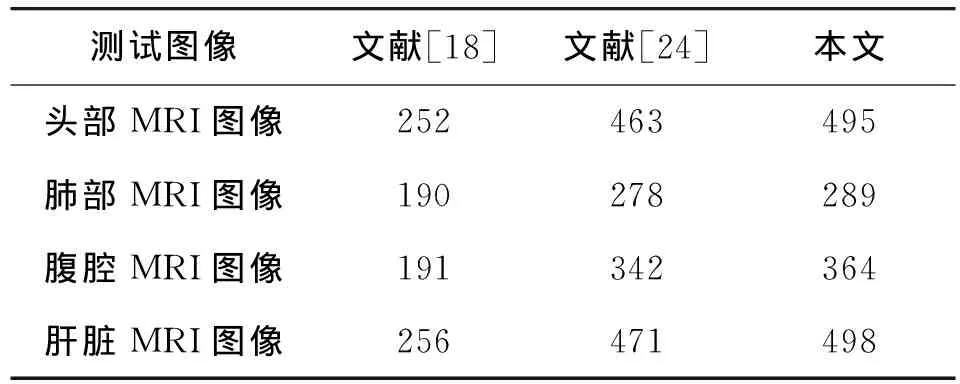
表8 容量对比Tab.8 Capacity comparison bit

4 结语

针对当前医学图像可逆水印算法抗攻击能力不足问题，本文提出一种基于深度残差网络的医学图像鲁棒可逆水印算法。首先，根据像素调整策略预处理医学图像，避免像素溢出；其次，利用深度残差模型自适应确定嵌入强度；再次，采用基于直方图平移和聚类算法嵌入与提取水印信息。实验结果表明：本文算法可以无损恢复医学图像，保证了医学图像的完整性；并且对于常见的信号攻击具有较好的稳健性，提高了可逆水印的鲁棒性；同时嵌入水印后的医学图像PSNR 值均达到36 dB 以上，较好地均衡了水印的不可见性和鲁棒性；此外，与现有算法相比，在嵌入容量上具有一定优势。本文算法在无损恢复医学图像的基础上，还可以抵抗常见的信号攻击，实现了对医学图像的版权保护。下一步的研究工作考虑将深度学习应用于整个医学图像版权保护算法中，在保证医学无损恢复的前提下，使得该算法对于攻击具有更好的普适性。