降雨入渗对人工填土斜坡稳定性影响研究

李 华，史文兵, 2*，张华湘(.贵州大学 资源与环境工程学院, 贵州 贵阳 550025; 2. 贵州大学 自然资源部喀斯特环境与地质灾害重点实验室, 贵州 贵阳 550025；.贵州省地质矿产勘查开发局04地质大队，贵州 都匀 558000)

对人工填土斜坡的稳定性影响的研究，前人在影响因素和机理方面已做出较深入的探讨。如应宏伟等[1]研究认为，人工填土堆筑速度过快，软土来不及固结以致土体强度低；栾茂田等[2]根据试验分析表明，低压实填土渗透性较好，降雨入渗降低土体有效强度；赵春宏等[3]通过对填土进行试验表明，土体孔隙水压力增加且具有突然性，水位上升引起静态液化导致斜坡稳定性降低；刘新喜等[4]通过数值模拟分析认为，强风化软岩高填方路堤压实度低或强降雨导致斜坡失稳；马莎等[5]研究认为，在暴雨作用下土体黏聚力和摩擦强度降低导致高填方斜坡失稳。可见，堆填速率过快、压实低、降雨、静态液化等是降低人工填土斜坡的稳定性的因素。对建于填土斜坡上的工程，降雨入渗因素是持续而可控的，而其他因素是难以改变的，因此，研究降雨入渗对人工填土斜坡稳定性的影响能为避免此类滑坡提供依据。

关于降雨对土体斜坡稳定性影响研究有了一定的水平和规模，如高润德等[6]通过研究单层粉质黄土模拟分析认为，土体的渗透性对非饱和土斜坡稳定性影响大；吴俊杰等[7]通过对单层土体计算分析认为非饱和土基质吸力对土坡稳定性影响显著，而单纯地下水位升高影响不明显；许建聪等[8]通过试验分析认为中深层碎石土斜坡失稳是由于降雨引起滑动面接触摩擦应力减小；张国超等[9]通过对间歇性降雨的数值分析表明，第一次降雨对斜坡稳定性影响最显著；高连通等[10]通过对单层堆积体数值模拟多场分析表明渗流场和位移场相似；冯凯文、温永福等[11-12]研究表明降雨通过降低有效应力和不同程度降低抗剪强度的方式降低斜坡稳定性。多数学者更局限于均质单层土斜坡，而物理力学差异大的人工填土和天然土组合斜坡体研究较少。

贵州定东小学斜坡为典型的填土-残坡积土多层组合斜坡，于2013年出现明显滑坡迹象，目前已有效治理。为探讨降雨对人工填土斜坡的影响，本文以治理前的贵州省定东小学斜坡为例，利用有限元Geostudio软件多个模块耦合分析斜坡稳定性，将是对人工填土斜坡研究的有益补充。

1 斜坡地质环境条件

1.1 斜坡工程地质条件

定东小学斜坡为侵蚀-溶蚀中低山谷地斜坡，位于贵州省贵定县定东乡农庄村的关坝河南岸，处于云贵高原东南部，属长江流域沅江水系清水江支流。区域内主要出露地层有第四系(Q)和志留系中统翁项组(S2w)，还发育一条东西走向陡倾正断层和宽缓的向斜，且地层近水平，其地震烈度为Ⅵ度，整体较稳定。研究区的地下水由西北向东南径流，排泄于低洼地带并汇入关坝河。斜坡上建设场坪时，其人工堆填土覆盖原有自然水沟和铁路路基排水涵洞。

1.2 斜坡体特征

定东小学斜坡是残坡积土堆填人工填土而成。据前期大量的钻探、浅井和物探等勘察资料，得出定东小学斜坡某工程地质剖面图(图1)。斜坡呈南高北低，高差为60 m；呈多级阶地，坡度较缓，约为10°，基岩岩层近水平，地下水位深浅变化，见季节性泉点，流量0.014～0.08 L/s。

1-第四系填土；2-第四系残坡积土；3-志留系翁项组；4-含碎石填土；5-含砾粉质粘土；6-泥质灰岩；7-水位线；8-潜在滑面。

斜坡体物质具有明显分带性(图2，a)。从浅到深分别为：人工填土层(Qml)由褐黄色粉质黏土及碎石构成，角砾和碎石含量30%左右，结构松散，高压缩性，透水性较高；残坡积土层(Qel+dl)为黄色粉砂质黏土，硬塑-软塑状，含大量角砾和碎石，角砾粒径为0.5～30 mm之间，约占20%，土体潮湿，浅井可见渗水(图2，b)，厚3～10 m；基岩层(S2w)为浅灰色中厚层粉砂质、泥质灰岩夹页岩，呈块状，上部为厚约5 m的强风化层，页岩遇水易软化，呈土状。

图2 钻探和浅井揭示的斜坡体物质特征Fig.2 Material characteristics of slope revealed by drilling and shallow wells

斜坡上操场和宿舍楼出现大量裂缝等斜坡变形现象，裂隙宽7～30 cm，部分呈上下错动，错距5～20 cm，其走向与坡面平行(图3)。

图3 定东小学操场和宿舍楼裂缝Fig.3 Cracks in the playground and dormitory building of Dingdong primaryschool

基岩比较稳定，深部无明显滑动，填土与残坡积土界线和岩土界线较清晰，为斜坡发生滑坡时的潜在滑移面。

2 数值计算模型建立

2.1 模型建立与参数选取

据斜坡的工程地质剖面和物质特征，利用有限元软件Geostudio建立共9 671个单元和29 516个节点的4层材料数值计算模型，并布设8个孔隙水压监测点(图4)。

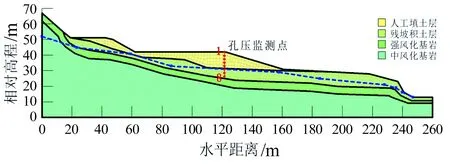
图4 斜坡数值计算模型Fig.4 Slope numerical calculation model

据勘察报告及文献[13-14]得出斜坡岩土体的物理力学参数(表1)。在土体渗透场中，饱和-非饱和理论通常认为非饱和状态下达西定律仍然适用，但其体积含水量和渗透系数是函数。在有限元SEEP模块中，土体的土水特征曲线可据饱和含水量和同类样本函数[15]计算而得，再基于土水特征曲线和饱和渗透系数，采用FREDLUND和XING法[15]估算得到两类土体的渗透系数函数(图5)。

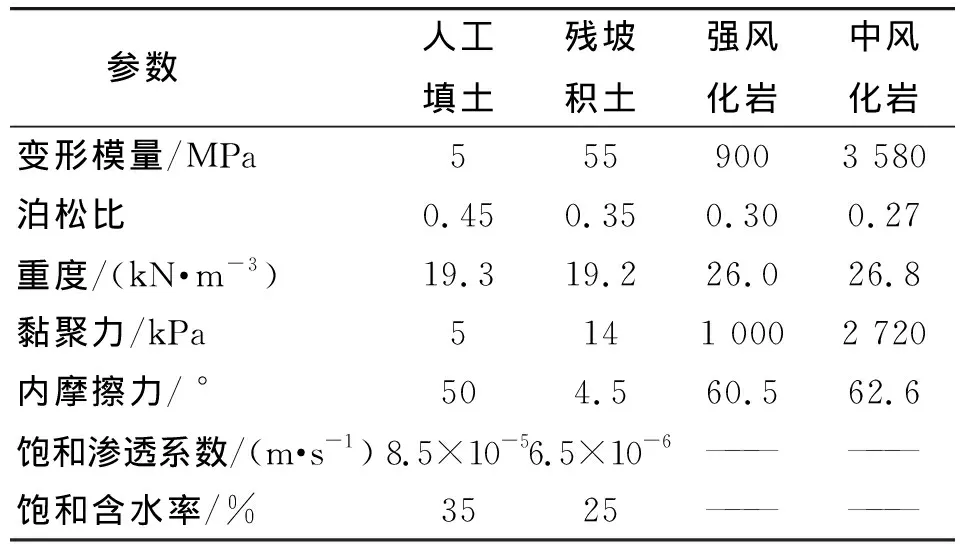
表1 岩土体物理力学参数Tab.1 Physical and mechanical parameters of rock and soil mass

2.2 定解条件及计算工况

定解条件：SEEP模块渗透场分析中，初始条件为斜坡实际地下水位线，土体的毛细水上升高度为3 m，即最大负孔压水头为3 m；填土坡面为不同等级的定流量入渗边界，流量等级为降雨量等级；泉点发育处以下坡面为潜在渗出边界。SLOPE模块稳定性分析中，潜在滑移面为岩土界面和填土与坡积土界面；SIGMA模块应变场分析中，斜坡左右边界固定竖直X位移，底部边界Y位移均固定。

本文重点探讨降雨入渗作用对斜坡作用机制和影响程度等的分析，因此，数值计算工况为不同降雨强度在极端持续降雨条件下稳定性变化情况。即填土后斜坡在不同降雨强度和原始斜坡在特大暴雨强度下持续2 d工况(表2)。

1-人工填土；2-残坡积土。图5 斜坡土体的土水特征曲线和渗透系数函数Fig.5 Soil-water characteristic curve and permeability coefficient functionof slope soil mass

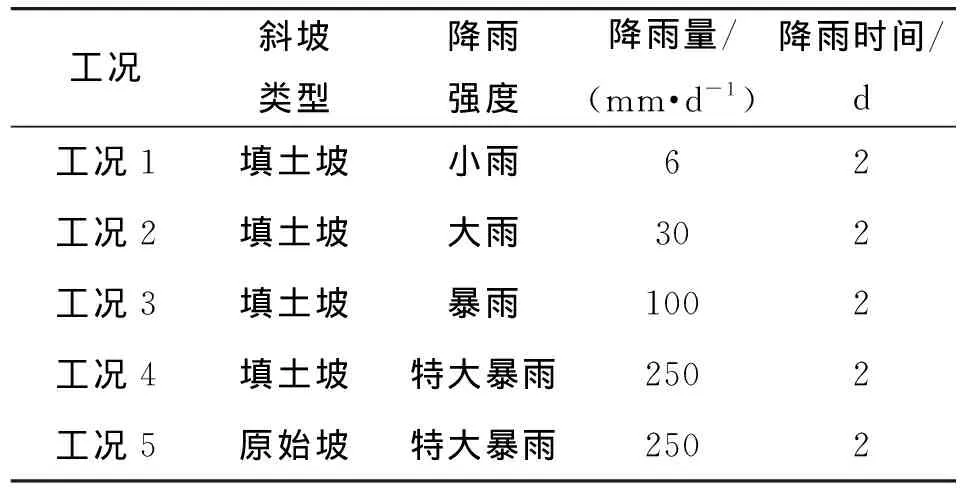
表2 计算工况条件Tab.2 Calculating operating conditions

3 多场耦合对斜坡稳定性的分析

3.1 降雨条件下斜坡渗透场特征

基岩透水性差，且对斜坡影响较小，因此不考虑基岩渗透作用。利用SEEP模块计算得出斜坡体在工况1—工况4的地下水流速云图(图6)，同时得出在工况4的水平距离为120 m处不同深度的孔隙水压力与降雨时间关系图(图7)。由图7可知，随着降雨强度增加，斜坡体内地下水位上升，土体含水量增加，渗透压力增加，导致地下水流速增大；在渗透性突变的填土与残坡积土界面近，地下水向下运动受阻聚集而向临空面方向运动，导致最大地下水流速集中于该界面附近，其最大流速达2.38×10-5m/s；降雨历时增加，斜坡土体孔隙水压力整体上大幅度增加，最大增量约50 kPa，而浅层负孔隙水压力(即基质吸力)先降为零，再转为正压继续增加，即斜坡非饱和土转为饱和土。

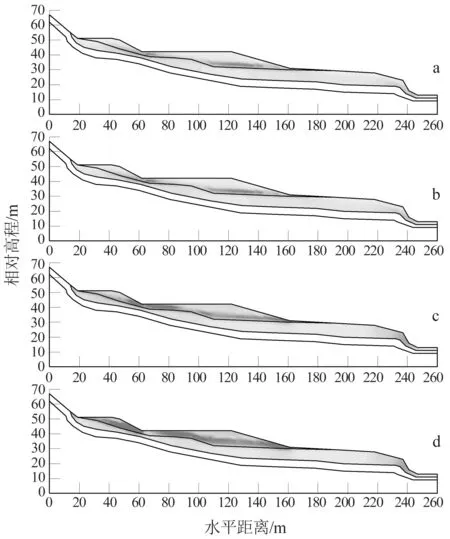
(地下水流速浅色小，深色大，范围为1.14×10-11～2.38×10-5m/s)a-小雨；b-大雨；c-暴雨；d-特大暴雨。图6 不同降雨强度持续降雨2天时地下水流速云图Fig.6 Groundwater flow velocitynephogram for two days of continuous rainfall with different rainfall intensity

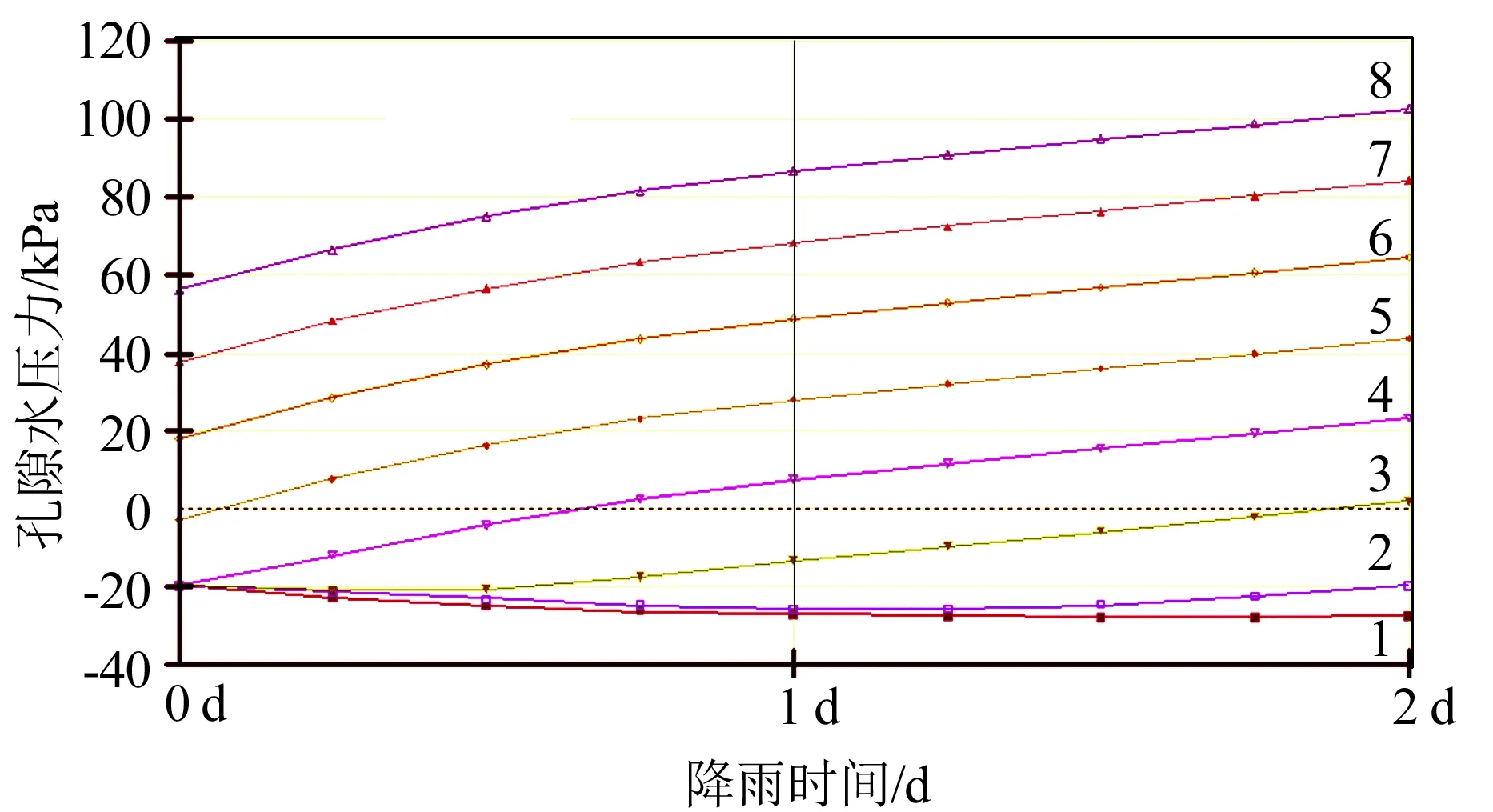
1—5为浅部填土层；6—8为深部残坡积土层。

3.2 渗透场耦合下的应变场特征

将SEEP模块计算出的瞬时孔隙水压力导入SIGMA模块进行耦合计算，得到斜坡的最大剪应变云图(图8)。由图8可知，降雨强度的增加，斜坡最大剪应变增加，最大值达0.122；最大剪应变集中于填土与残坡积土界面附近前端坡度较大处，与地下水流速较相似性；同时最大剪应变集中部位与实际的斜坡体上宿舍楼和操场出现大量裂缝等(图3)变形迹象一致。

(最大剪应变值浅色小，深色大，范围为5.04×10-9 ～1.22×10-1)a-小雨；b-大雨；c-暴雨；d-特大暴雨。图8 不同降雨强度持续降雨2 d时最大剪应变云图Fig.8 Maximum shear strainnephogram for two days of continuous rainfall with different rainfall intensity

3.3 降雨条件下斜坡稳定性

上述可知，降雨入渗作用引起人工填土斜坡土体内地下水流速增加且集中于填土与残坡积土界面附近等渗透场变化；同时，也引起剪应力集中导致最大剪应变不断集中于填土与残坡积土界面前端的应变场变化。总之，降雨渗透作用对人工填土斜坡的填土与残坡积土界面影响最强烈，结合浅井、钻芯和物探揭示的斜坡体物质结构特征可得，该界面为人工填土斜坡发生整体性滑坡的最大潜在滑移面。

将SEEP模块计算出斜坡土体内瞬时孔压耦合进入SLOPE模块，拟定填土与残坡积土界面为滑动面，采用Morgenstern-Price法计算出斜坡工况1—工况4不同降雨持续时间的稳定性(图9)。由图9可知，降雨历时一定，斜坡稳定系数随降雨强度增加而降低；降雨强度一定，斜坡稳定系数随降雨持续时间增加而降低；降雨强度低于大雨时，稳定系数缓慢降低，而当降雨强度高于暴雨时，稳定系数急剧下降；当暴雨持续降雨2 d或特大暴雨持续1.25 d时，斜坡稳定系数从1.133降至1.0以下，斜坡变为不稳定状态，此时斜坡可能会沿填土与坡积土界面发生整体性滑动。

图9 不同降雨强度和持续时间的斜坡稳定系数Fig.9 Stability coefficient of slopes with different rainfall intensities and durations

同时发现，降雨前、后期对斜坡稳定性的影响具有较明显的差异。降雨时间为0 d、1 d和2 d的稳定系数FS0、FS1、FS2，则降雨前期对斜坡稳定性影响占比定义为{(FS1-FS0)/[(FS1-FS0)-(FS2-FS1)]}×100%。根据图9数据，计算得出特大暴雨、暴雨、大雨和小雨的前期降雨影响占比56.6%、59.7%、79.5%和81.1%，均大于50%，且随降雨强度降低而增加。以上表明，前期降雨对斜坡稳定性影响比后期降雨的影响大，且降雨强度越小，降雨前期影响大的效应越强。

3.4 填土前后斜坡稳定性分析

定东小学原始斜坡潜在滑动面为岩土界面，填土后潜在滑动面为填土和残坡积土界面，通过模拟计算工况4和工况5稳定系数结果(表3)。由表可知，在特大暴雨强度持续降雨2 d时，填土后的斜坡稳定系数为0.935，斜坡可能沿着岩土界面发生整体性滑动；而原始斜坡，即便在特大降雨持续2 d后，其稳定系数仍为1.399，斜坡整体较稳定。可见，填土导致是导致斜坡失稳的重要因素。

表3 填土前后斜坡稳定系数Tab.3 Slope stability coefficient before and after filling

4 降雨对填土斜坡稳定性影响机理

填土因素是降低人工填土斜坡稳定重要因素。一方面，压实低填土本身力学强度弱，增加原始斜坡体自重，从而降低斜坡稳定性；另一方面，填土压实性低，结构疏松，导致土体渗透性较好，即填土具有增强降雨因素对斜坡稳定性影响的作用。

降雨条件下，雨水下渗，地下水位线上升，土体孔隙水增加，大部分非饱和土转为饱和土，斜坡自重增加，导致斜坡下滑力不断增大；由于地下水集中于填土与坡积土界面附近的填土层部位，地下水流速不断增大，引起渗透压力增大，导致斜坡下滑力增大；重力场和渗透场作用下，填土与坡积土界面的临空面附近剪应力集中，当超过极限抗剪强度时，斜坡沿着某潜在剪切滑移面发生剪切位移，导致此处剪应变不断增大。同时，斜坡体非饱和土，随着孔隙水的增加，负孔隙水压力逐渐降低至零，导致土体基质吸力降低，削弱了斜坡的抗剪强度；斜坡体饱和土孔隙水压力并不断增加，导致斜坡有效强度减弱，从而降低斜坡体的总抗滑力。随着下滑力不断增加，抗滑力不断减少，稳定系数(抗滑力下滑力之比)逐渐降低，即斜坡稳定性不断降低。当潜在滑面的总下滑力大于总抗滑力，斜坡将沿着该滑面向临空面发生整体性滑动而导致斜坡失稳。

5 结论

本文考虑降雨渗透作用对具有残坡积土层和人工填土层的斜坡稳定性的影响，得出以下结论：

(1)填土与坡积土界面渗透性差异引起降雨条件下填土斜坡地下水流速和最大剪应变集中于该界面附近。

(2)降雨条件下，斜坡体渗透场和应变场变化较相似，地下水流速和最大剪应变与降雨强度均呈反比。

(3)填土对降雨影响斜坡稳定性起一定增强作用，且填土与残坡积土界面为斜坡失稳的最大潜在滑移面。

(4)降雨持续时间和降雨强度增加，斜坡稳定性降低；前期降雨对斜坡稳定性影响比后期大，且降雨强度越小，此效应越强。

(5)降雨入渗降低斜坡稳定性的主要作用机理：地下水流速增加导致渗透压力增加，使剪应力集中而增加剪应变；孔隙水压力增加和基质吸力降低，导致降低斜坡体有效强度和抗滑力；土体容重增加，下滑力增加。