具有广义C-凸性的一类分式规划的对偶

李 钰，严建军，李江荣(. 延安大学 数学与计算机科学学院, 陕西 延安 76000; 2. 延安职业技术学院, 陕西 延安 76000)

近年来，随着凸性理论在优化领域的广泛应用，涌现出丰硕的研究成果。文献[1-6]提出了(C,α,ρ,d)-凸函数，并对包含此类凸性的多目标、分式规划等问题的最优性条件与对偶性定理进行了研究。受上述文献启示，作者结合文献[7-8]中提出的广义(C,α,ρ,d)K,θ-凸性，讨论了一类多目标半无限分式规划的Mond-Weir型对偶问题。

1 基本概念

定义1[1]称函数C:X×X×Rn→R在Rn上关于第三个变元是凸的, 若∀(x,x0)∈X×X, ∀y1,y2∈Rn, 有

C(x,x0)(λy1+(1-λ)y2)≤λC(x,x0)(y1)+(1-λ)C(x,x0)(y2), ∀λ∈(0,1)。

在文中, 均假设∀(x,x0)∈X×X, 有C(x,x0)(0)=0。

定义2[1]设函数f:X→R是局部Lipschitz函数, 若∃α:X×X→R+{0},ρ∈R,d:X×X→R+, 如果∀x∈X, 有

(f(x)-f(x0))/α(x,x0)≥C(x,x0)(ξ)+ρd(x,x0)/α(x,x0), ∀ξ∈∂f(x0),

则称函数f在x0处是(C,α,ρ,d)-凸函数。

bi(x,x0)φ(fi(x)-fi(x0))≥αi(x,x0)C(x,x0)(ξi)+

ρid2(θi(x,x0)), ∀ξi∈∂Kfi(x0),

则称函数f=(f1,…,fp)在x0∈X处是广义(C,α,ρ,d)K,θ-凸函数。

如果函数f在X上每一点处为广义(C,α,ρ,d)K,θ-

凸函数, 则称f在X上是广义(C,α,ρ,d)K,θ-凸函数。

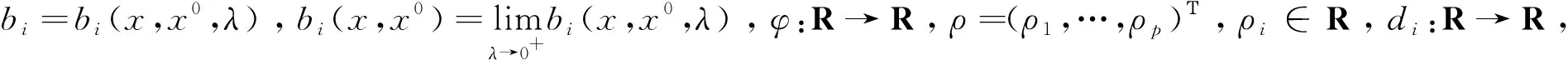
bi(x,x0)φ(fi(x)-fi(x0))<(≤)0⟹αi(x,x0)C(x,x0)(ξi)+ρid2(θi(x,x0))<0，∀ξi∈∂Kfi(x0),

则称函数f=(f1,…,fp)在x0∈X处是广义(C,α,ρ,d)K,θ-(严格)伪凸函数。

如果函数f在X上每一点处为广义(C,α,ρ,d)K,θ-(严格)伪凸函数, 则称f在X上是广义(C,α,ρ,d)K,θ-(严格)伪凸函数。

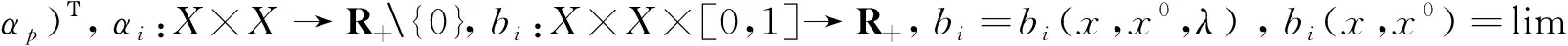
bi(x,x0)φ(fi(x)-fi(x0))≤(<)0⟹αi(x,x0)C(x,x0)(ξi)+ρid2(θi(x,x0))≤0,∀ξi∈∂Kfi(x0),

则称函数f=(f1,…,fp)在x0∈X处是广义(C,α,ρ,d)K,θ-(弱)拟凸函数。

如果函数f在X上每一点处为广义(C,α,ρ,d)K,θ-(弱)拟凸函数, 则称f在X上是广义(C,α,ρ,d)K,θ-(弱)拟凸函数。

对于下述规划:

s.t.hj(x)≤0,j∈J,

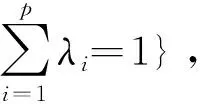
考虑(MSIFP)的Mond-Weir型对偶:

2 主要结果

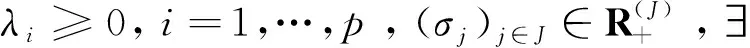
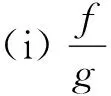
(ii) 对于j∈J(y),h在y处是广义(C,β,ρ2,d)K,θ-凸函数。

(iii) 广义Slater条件成立, 即x0∈X, 有hj0(x0)<0,j0∈J(y), 且σj0>0。

(iv)α1=…=αp=β1=…=β(J)=δ。

(v)b1(x,y)>0,b2(x,y)>0; 若a≤0, 则φ1(a)≤0; 若a<0, 则φ2(a)<0。

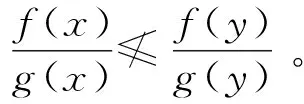
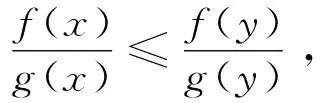
且∃i0, 1≤i0≤p,i≠i0, 使

据(i)和(v), 得

则

αi(x,y)C(x,y)(ξi)+ρ1id2(θi(x,y))≤0,

因为λ∈Λ+, 所以

当x0∈X, 有

(1)

由(iii), 可得

hj0(x0)<0=hj0(y),j0∈J(y),

即有

hj0(x0)-hj0(y)<0,

又由(v), 知

b2j0(x0,y)φ2(hj0(x0)-hj0(y))<0,

由(ii), 有

βj0(x0,y)C(x0,y)(ζj0)+ρ2j0d2(θj0(x0,y))<0,∀ζj0∈∂Khj0(y),

用σj0>0乘以上式, 有

βj0(x0,y)C(x0,y)(σj0ζj0)+σj0ρ2j0d2(x0,y)<0, ∀ζj0∈∂Khj0(y),

(2)

因σj≥0,j∈J(y),j≠j0及第二个约束条件, 得

hj(x0)≤0≤hj(y),

又由(v)和(ii)可知, ∀ζj∈∂Khj(y), 有

βj(x0,y)C(x0,y)(σjζj)+σjρ2jd2(θj(x0,y))≤0,j∈J(y),j≠j0,

当j∈J(y)(j≠j0)时，对上式求和, 得

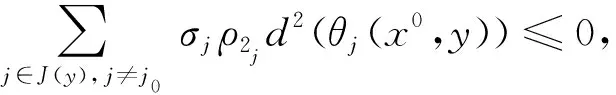
(3)

当j∈JJ(y)时, 令σj=0, 有

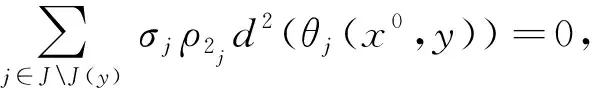
(4)

将式(1)―(4)相加, 结合函数C的凸性和(iv), 可得

由(vi), 知

≤0,

这与(MSIFD)的第一个约束条件矛盾！所以

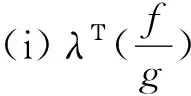
(ii) 当j∈J(y)时,h在y处是广义(C,β,ρ2,d)K,θ2-拟凸函数。

(iii)α=β1=…=β(J)=δ。

(iv)b1(x,y)>0,b2(x,y)>0; 若a<0, 则φ1(a)<0, 若a≤0, 则φ2(a)≤0。

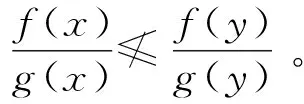
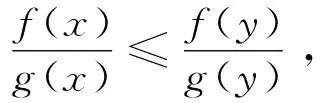
由于λ∈Λ++, 故

据(iv), 得

由(i)有

α(x,y)C(x,y)(ξ)+ρ1d2(θ1(x,y))<0,

(5)

根据σj≥0,j∈J(y)和第二个约束条件, 得

hj(x)≤0≤hj(y),

由(iv)和(ii)，有

βj(x,y)C(x,y)(σjζj)+σjρ2jd2(θ2j(x,y))≤0,∀ζj∈∂Khj(y),j∈J(y),

当j∈JJ(y)时, 令σj=0, 可知

(6)

式(5)、(6)相加，结合函数C的凸性与(iii), 得

依(v)知

这与(MSIFD)的第一个约束条件矛盾！所以

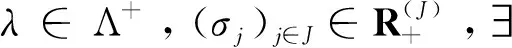
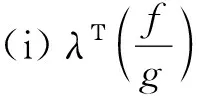
(ii) 当j∈J(y)时,h在y处是广义(C,β,ρ2,d)K,θ2-拟凸函数。

(iii)α=β1=…=β(J)=δ。

(iv)b1(x,y)>0,b2(x,y)>0; 若a≤0, 则φ1(a)≤0, 若a≤0, 则φ2(a)<0。

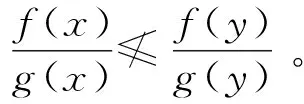
证明证明类似定理2。

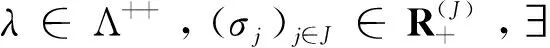
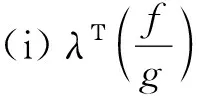
(ii) 对于j∈J(y),h在y处是广义(C,β,ρ2,d)K,θ2-严格伪凸函数。

(iii)α=β1=…=β(J)=δ。

(iv)b1(x,y)>0,b2(x,y)>0; 若a<0, 则φ1(a)<0, 若a≤0, 则φ2(a)<0。

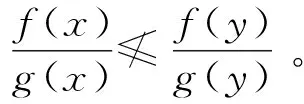
证明证明类似定理2。

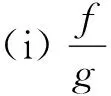
(ii) 对于j∈J(y),h在y处是广义(C,β,ρ2,d)K,θ-凸函数。

(iii) 广义Slater条件成立, 即x0∈X, 有hj0(x0)<0,j0∈J(y), 且σj0>0。

(iv)α1=…=αp=β1=…=β(J)=δ。

(v)b1(x,y)>0,b2(x,y)>0; 若a<0, 则φ1(a)<0, 若a≤0, 则φ2(a)<0。

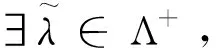
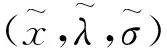
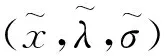
易知(MSIFP)与(MSIFD)有相等的目标函数值。

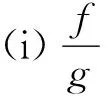
(ii) 当j∈J(y)时,h在y处是广义(C,β,ρ2,d)K,θ-拟凸函数。

(iii)α1=…=αp=β1=…=β(J)=δ。

(iv)b1(x,y)>0,b2(x,y)>0; 若a<0, 则φ1(a)<0, 若a≤0, 则φ2(a)<0。

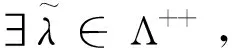
证明证明类似定理5。

3 结语

本文在已有文献提出的新广义凸性概念基础上，针对包含此类广义凸性的分式规划的对偶问题进行了探讨，得到的结果丰富了广义凸性和最优化的有关理论,可进一步研究其Wolfe型对偶性、鞍点等内容。