基于广义似然比检验的磁悬浮轴承位移传感器故障诊断方法
程 鑫,吴 惠,董家伟,王宁经
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.湖北省磁悬浮轴承工程技术研究中心,湖北 武汉 430070)
磁悬浮轴承是利用磁场力支承转子,具备无机械接触、高转速、无需润滑、寿命长等显著优点[1-2],主要由电磁执行器、控制器、转子系统以及传感器构成[3]。其中位移传感器是磁悬浮轴承系统的重要组成之一,其通过实时测量转子的位置,以构建闭环系统来提供期望电磁力,维持转子系统稳定。
磁悬浮轴承中常采用电涡流传感器,但其工作时需靠近转子,工作环境较恶劣,易出现故障。冗余传感器技术采用多个传感器同时工作,当某个传感器出现故障,依赖其冗余布局,控制器会舍弃故障器件,利用余下的传感器构建新的测量模型继续维持位置控制闭环工作,可切实有效地提高磁悬浮轴承的可靠性[4-5],但需要设计有效的诊断机制,准确定位故障传感器。
信任度矩阵分析与小波信号分析是两种常见的传感器故障诊断方法。其中,信任度矩阵是对n(n>2)个传感器输出值进行相互比较,检验彼此的支持度,从而排除故障信号[6];而小波信号分析将传感器时间信号映射到时间—尺度片面上,检验信号的极大值点,从而判断信号是否出现故障[7]。但以上方法皆通过设定阈值来检验是否出现故障,对于输入量频繁变换的系统故障诊断效果不佳,当超出阈值时,无法判断是否是由于信号频繁变换而引起的还是由于故障引起的。
广义似然比检验是尼曼和皮尔逊在1928年提出,用于解决假设检验中构造统计量的困难,文献[8]分析了用于冗余传感器测量系统故障检测与隔离(fault detection and isolation,FDI)的广义似然比检验(generalized likelihood ratio test,GLRT)方法,并进行修正;文献[9]将广义似然比检验用于船舶惯性导航系统(ship′s inertial navigation system,SINS),提高系统可靠性,验证了该原理并提出改进;文献[10]采用基于神经网络的奇偶向量补偿方法来提高多传感器斜置系统故障检测能力,减小系统的虚警率。文献[11]将广义似然比检验用于水下声矢量信号处理,对波数域数据进行广义似然比检验,提升系统在噪声条件下的系统增益与恒虚警率特性;文献[12]提出了一种新的广义似然比检验方法,用于处理非线性系统中的故障检验问题,并基于非线性GLRT方法,进一步分析了故障隔离以及非突发故障估计问题。文献[13]在臭氧浓度检测系统中引入约束广义似然比检验,用于解决有臭氧污染而引发的异常检验问题。
笔者引入广义似然比检验法对磁悬浮轴承的位移传感器系统进行故障诊断,该方法将传感器组的信号进行处理,根据设置的阈值来鉴别出传感器信号发生错误时产生的异常信号,从而实现故障诊断的目的,相比于信任度矩阵法对比同一维度的多个传感器值,该方法可以在一个维度上仅仅需要一个传感器,大大减少传感器的使用。
笔者主要针对磁悬浮轴承位移传感器系统,引入广义似然比检验法,采用MATLAB建立数学模型并进行仿真,对轴承系统传感器信号进行故障检验与处理,最终得到系统的位移反馈信号,用于控制器的处理。
1 位移传感器硬件冗余与故障分析
常规的电涡流位移传感器的故障存在多种方式,一般可分为脉冲故障、固定偏差故障、周期性干扰、开路故障、短路故障和漂移故障等。笔者主要针对短路故障、开路故障、脉冲故障、固定偏差故障和周期性干扰故障进行研究,其中开路故障和短路故障对系统影响较大,会使系统完全无法工作,而脉冲故障、固定偏差故障和周期性干扰故障对系统影响相对较小。传感器故障类型及原因如表1所示。

表1 传感器故障类型及原因
冗余传感器布置如图1所示。其中图1(a)为交叉冗余方式,两个传感器安装在水平与竖直方向上,第三个传感器安装在斜45°,传感器正常运行时采用S1和S2传感器,一旦这两个传感器中有一个出现故障时,启用S3传感器。进行故障诊断时,3个传感器测量两个自由度难以获得良好的诊断结果,为了改进系统性能,笔者添加第4个传感器,如图1(b)所示。图1(b)为交叉冗余方式改进型,传感器正常运行时采用S1和S2传感器,一旦这两个传感器中有一个出现故障时,就启用备用的S3和S4传感器构建新的测量系统,并通过坐标转换进行位置换算,这里仅考虑图1(b)中传感器的布置形式。
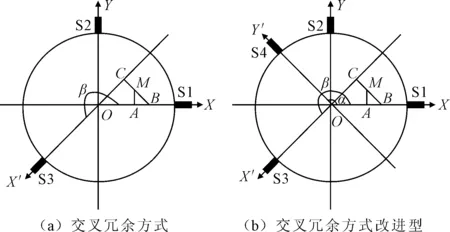
图1 传感器冗余布置形式
如图1(b)所示坐标系中,α=135°,β=225°,可知:
dx′=-OC=-OBcos (180°-β)=(OA+
AB)cosβ=[OA+AMtan (β-180°)]cosβ=
OAcosβ+AMsinβ=dxcosβ+dysinβ
(1)
同理:
dy′=dxcosα+dysinα
(2)
O为磁悬浮转子的轴心;dx,dy,dx′,dy′分别为位移矢量在X,Y,X′,Y′4个坐标轴的投影,其中dx,dy即磁悬浮转子在水平与竖直方向的位移。
us1=Kdx,us2=Kdy,us3=Kdx′,us4=Kdy′
(3)
us1=Vs1-Vs10,us2=Vs2-Vs20,
us3=Vs3-Vs30,us4=Vs4-Vs40
(4)
式中:K为传感器变化增益,K=8.333 V/mm;us1,us2,us3和us4为传感器输出值的偏移量;Vs1,Vs2,Vs3和Vs4为S1,S2,S3和S4传感器的输出值;Vs10,Vs20,Vs30和Vs40为标定的传感器中心位置的坐标值,即转子刚好悬浮在中心位置时传感器S1,S2,S3和S4的输出值。
根据式(1)~式(3),可以确立冗余测量方程Zo=HX,式中,Zo∈R4表示4个传感器的理论输出偏移量;X∈R2表示系统待测量的位移量;H∈R4×2表示传感器配置的安装矩阵。代入数据得:
(5)
2 基于广义似然比检验的冗余传感器故障诊断
2.1 广义似然比检验法
文献[14]中介绍了广义似然比检验与奇偶方程,假定系统有m个传感器,测量n个状态,则存在测量方程为:
Z=Zo+ε+f=HX+ε+f
(6)
式中:Z表示传感器的实际输出;ε∈Rm表示传感器组的噪声输出且E(ε)=0,D(ε)=s2;f∈Rm表示传感器的故障输出,当系统没有出现故障时,f=0。文中m=4,n=2。
构造奇偶方程如下:
p=VZ
(7)
式中:p∈Rm-n表示系统的奇偶向量;V∈R(m-n)×m为解耦矩阵,并且VH=0,VVT=Em-n,此时式(7)可以转换为,
p=Vε+Vf
(8)
此时,奇偶向量不仅与噪声有关,同时与故障输出有关。
定义的故障判决函数FD为:
FD=pTp
(9)
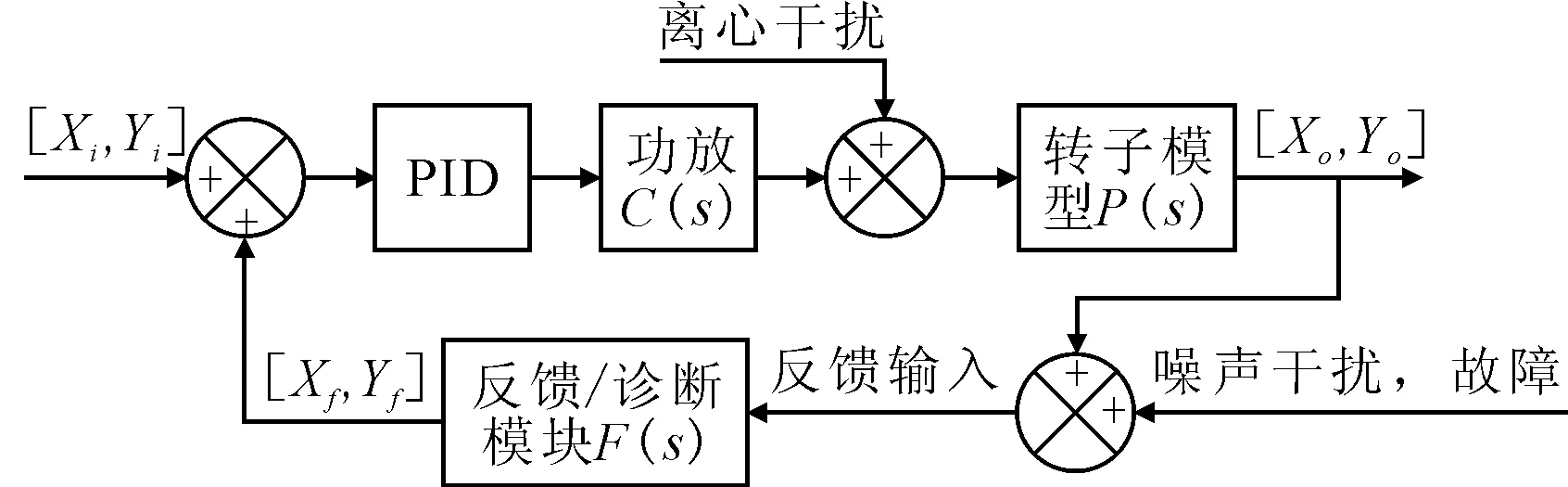
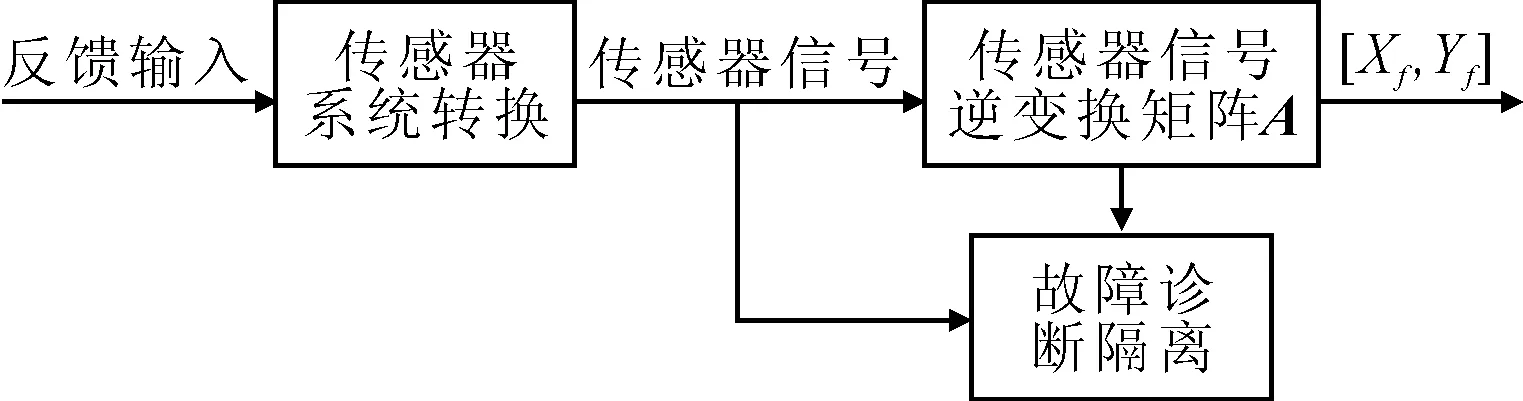
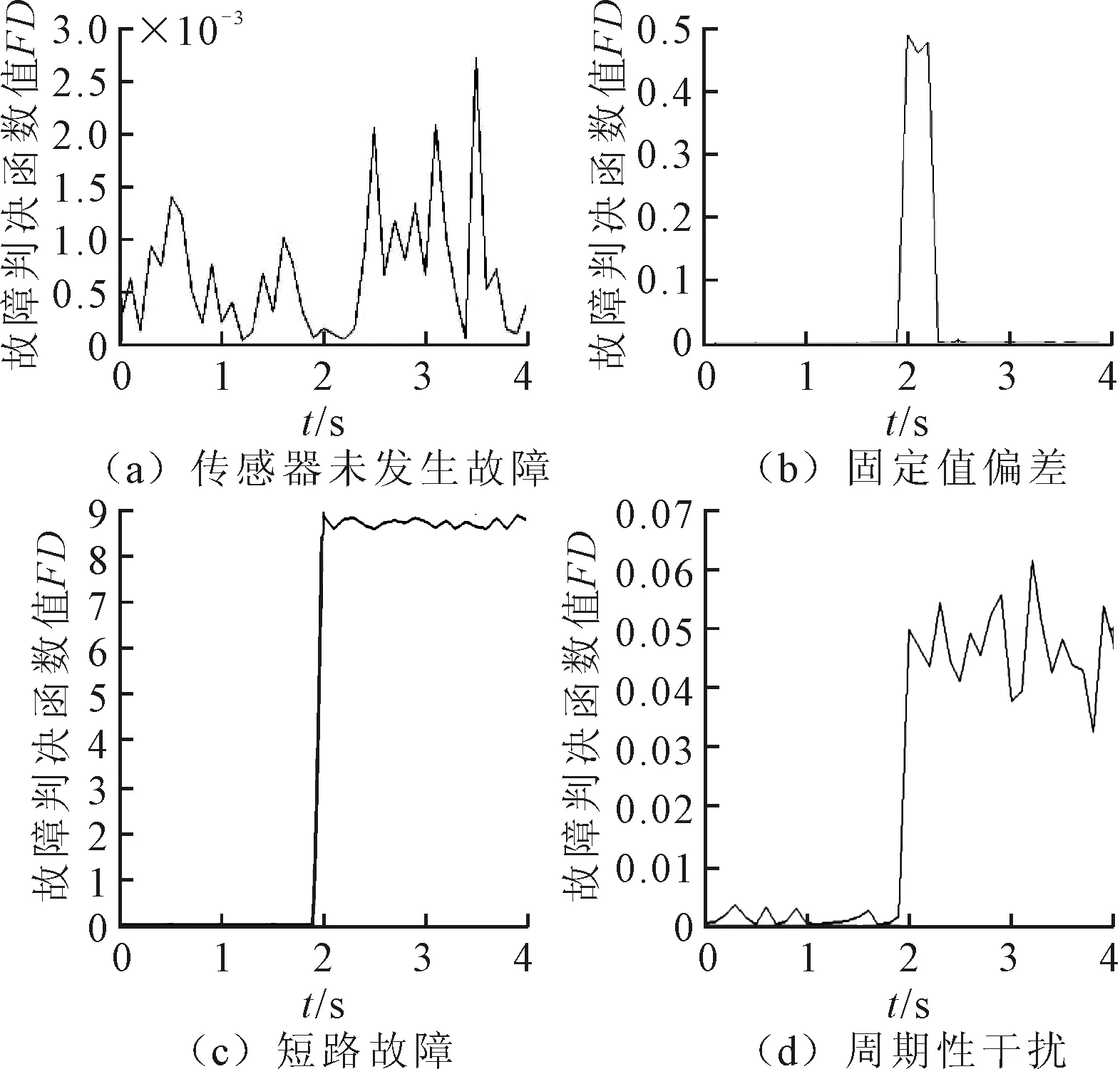
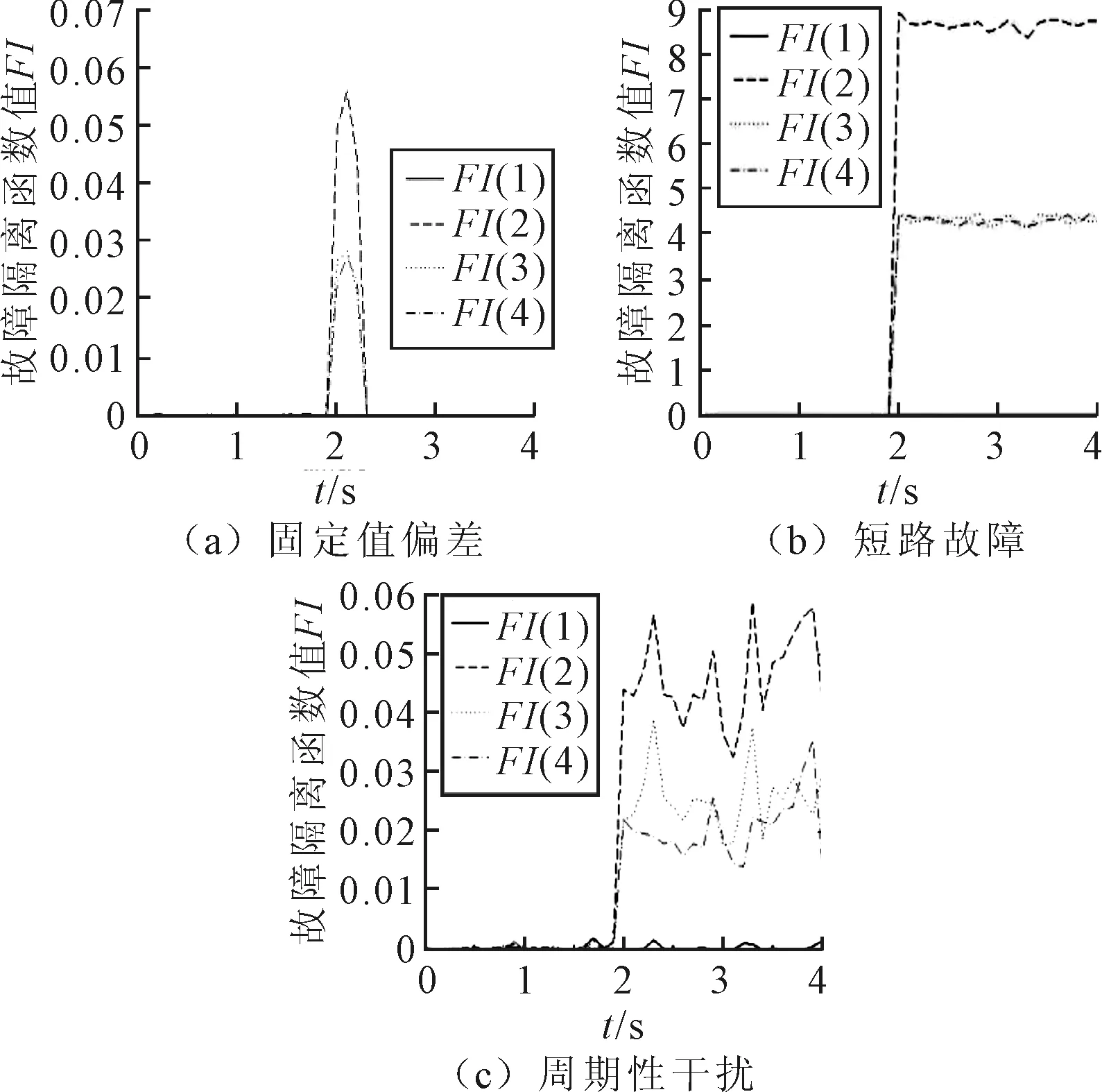
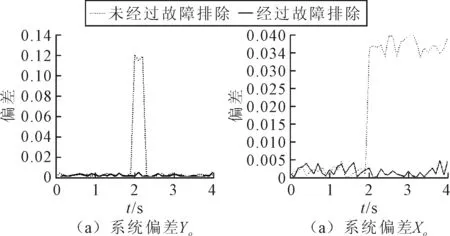
显然,FD服从自由度为m-n的卡方分布,可以根据所设置置信概率定义阈值Td,当FD 检测到故障之后,定义的故障隔离函数FI(j)为: (10) 式中:Vj表示V的第j列,若FD(k)=max{DF(j)},(j=1,2,…,n),则表示第k个传感器出现了问题(因为本研究是为磁悬浮轴承的容错控制提供基础的,因此认为只有一个传感器发生了故障)。 根据解耦矩阵性质VH=0,VVT=Em-n,可以利用正交投影来构造矩阵,具体变化如下: W=E-H(HTH)-1HT (11) 取W的前m-n行,将其进行Gram-Schmidt正交化,并作单位化处理: (12) 带入数据得: (13) 经验证,矩阵V满足所要求的条件。 图2 仿真系统基本框图 对于诊断/反馈模块F(s),仿真框图如图3所示。反馈输出由传感器理论输出、故障输出与噪声信号构成,对反馈信号式(6)计算Z=HX+ε+f,得到传感器信号Z,Z∈R4,分别表示4个传感器的信号;传感器信号根据公式(7)~式(9)进行故障诊断,分别得到故障判决函数FD与故障隔离函数FI,根据设置的阈值T,对FD进行诊断。当FD大于T时,表示传感器信号出现故障,FI(k)取最大值时的k表示第k个传感器出现故障,并根据诊断结果选择相应的逆变换矩阵Ai,S=AiZ,S=[Xf,Yf]表示位移,当S1或S2发生故障时,选择A1,反之选择A2,当没有发生故障时,默认使用A2。A1,A2表达式为: 表2 系统相关参数 (11) 图3 诊断/反馈模块F(s)基本框图 设定Xo为0.2 mm,Yo为0.5 mm。当系统未发生故障时,判决函数如图4(a)所示,由于存在数据野点,数据波动较大,波动程度取决于干扰信号的方差,方差越大,波动越小。根据未发生故障时的图像设置阈值,为了减少数据野点的干扰,判断时每5个采样点统计一次,其中连续3个点超出阈值,则视为出现故障。 当t=2 s时,给传感器S2一个固定值偏差,持续0.3 s,此时判决函数如图4(b)所示,在t=2 s时产生一个尖锐信号,当偏差值越大时,峰值越大;此时故障隔离函数如图5(a)所示,当出现偏差时,此时FI(k)出现明显的差异,FI(k)在k=2时取峰值。 当t=2 s时,传感器S2发生短路故障,此时判决函数如图4(c)所示,2 s之后的判决函数数值超出未发生故障时数值,并且数量级较大,可以反映传感器发生故障的程度较大。此时故障隔离函数如图5(b)所示,当出现偏差时直到仿真结束,此时FI(k)出现明显的差异,FI(k)在k=2时取峰值。 当t=2 s时,给传感器S2峰值为1 V,频率为5 Hz的电源干扰信号,此时判决函数如图4(d)所示,2 s之后的判决函数出现波动,波动程度取决于采样时间,采样时间越短,变化越明显,但相比于短路故障,此时超出阈值但是数量级相对较小。此时故障隔离函数如图5(c)所示。当出现偏差时,此时FI(k)出现明显的差异,并且具备周期性,FI(k)在k=2时取峰值。 图4 故障判决函数 图5 故障隔离函数 以固定偏差为例,给系统注入误差,将系统排除传感故障后所得到的反馈位移[Xf,Yf]与系统实际位移[Xo,Yo]进行比较,对系统的偏差值进行分析,如图6(a)所示。在未出现故障时两者的偏差大致相等,当t=2 s传感器S2出现故障时,未经过排除故障处理信号会在竖直位移Yo上产生较大的偏差,而经过处理的偏差依旧稳定在较小的数量级。 改变故障类型,当t=2 s时给传感器S1一个周期性的干扰,直到仿真结束,如图6(b)所示,当出现偏差时,未经过排除故障处理信号会在水平位移Xo上产生较大的偏差,而经过处理的偏差依旧稳定在较小的数量级。 图6 系统偏差值 笔者利用广义似然比检验对磁悬浮轴承冗余位移传感器进行故障诊断,并进行仿真。由仿真结果可知,将广义似然比检验用于磁悬浮轴承冗余位移传感器的故障诊断具有一定可行性,实际工程应用中,系统解耦矩阵V取决于传感器配置的安装矩阵H,H不仅与传感器配置有关,同时与传感器精度、安装手法等有关,可以适当对H进行改进从而得到最优的处理结果,使虚警率降低,故障隔离效果更明显。 广义似然比检验根据判断阈值来诊断故障,当诊断结果未达标时视为出现故障,并列举了该系统中常见的故障类型,均符合推导结果。但是针对文中所列举的故障类型,该方法没有对不同故障类型的诊断结果做甄别,即未能区别不同故障类型,故本方法仅仅判断出是否发生故障并摒弃故障传感器的信号,无法判断故障类型,可在后续研究中深化。2.2 解耦矩阵构造
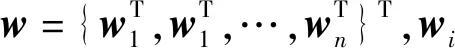
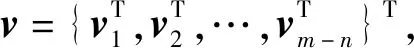
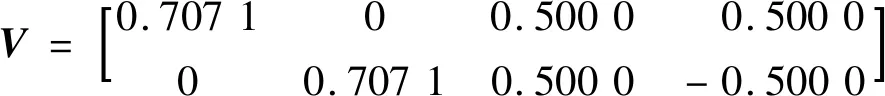
3 磁悬浮轴承位移传感器系统仿真


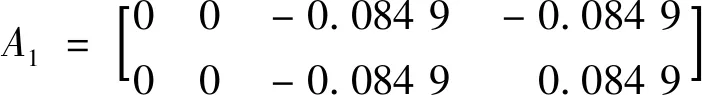
4 结论

