核心素养引领下的经典问题解答新思路探究——由一道初三上学期期中考试题说起

江苏省苏州市相城区东桥中学 凌 健

有一年初三数学第一学期期中试卷第28题的第（3）小题，笔者任教的两个班得分率特别低，得满分的寥寥无几。为此笔者对这个题目进行了深入的研究，试图找出症结所在，通过思考问题的本质，找到了其中的共性和特性。本文给出对该题的一题多解，解后反思及教学反思，期待与同行交流。

一、试题呈现

如图1，在平面直角坐标系中，点A的坐标是（8，0），点的坐标是（0，6），点P从点O开始沿轴向点以1cm/s的速度移动，点Q从点B开始沿y轴向点以相同的速度移动，若P、Q同时出发，移动时间为t（s）（0＜t＜6）。

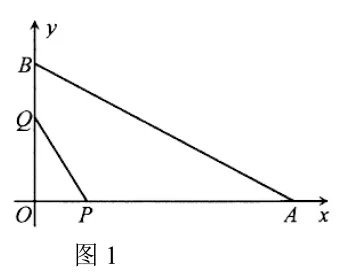
图1

（1）当PQ//AB时，求t的值；

（2）是否存在这样t的值，使得线段PQ将△AOB的面积分成1:5的两部分。若存在，求出t的值；若不存在，请说明理由；

（3）当t=2时，试判断此时△POQ的外接圆与直线AB的位置关系，并说明理由。

二、解法展示

问题（3）要判断当t=2时△POQ的外接圆与直线AB的位置关系，先要计算出d和r，再通过d和r比较大小进行判断。由题意可知0P=2，OQ=4，△POQ是直角三角形，所以外接圆圆心在PQ中点M（1，2）处以只要求出MH（如图2）的长度即可。

图2

解法1：利用等积法求线段MH的长度。

如图 3，连接 MB、MA、MO。

因为 S△AOB=S△ABM+S△AOM+S△BOM，

S△AOB=24，S△BOM=3，S△AOM=8，所以 S△ABM=13.

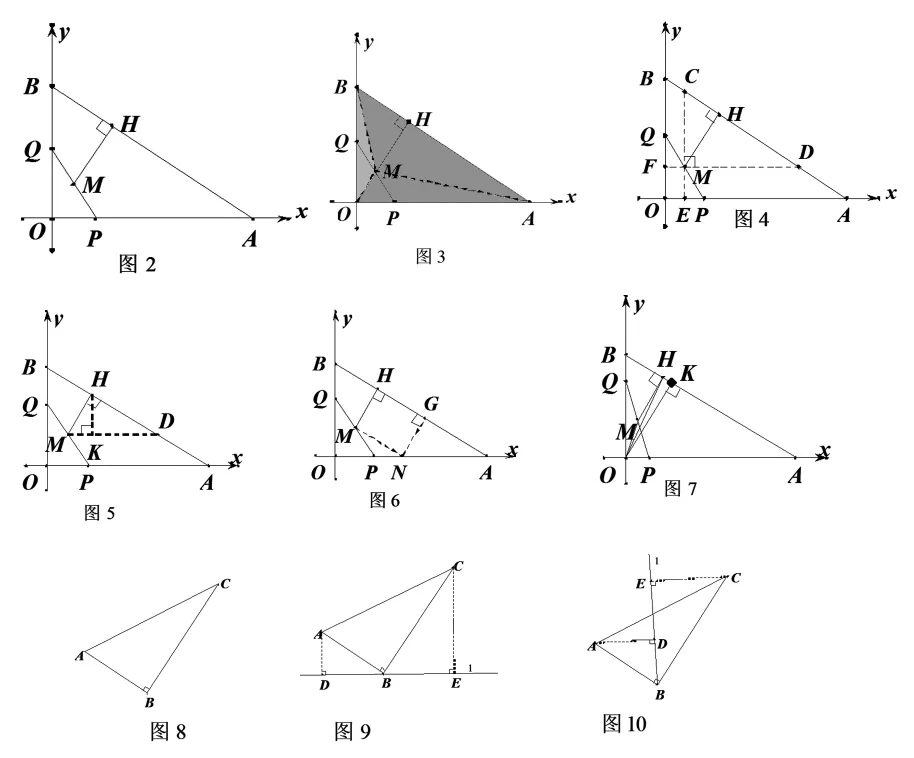
图3

解法2：构造相似模型求线段MH的长度

如图4，过点M作ME⊥x轴于E，交AB于点C；过点M作MF⊥y轴于F，交AB于点D。

图4

解法3：通过增量巧设简化相似计算过程

如图5，过点M作MD//x轴，交AB于点D；过点H作HK⊥DM于K。由题意可知，△MHK∽△BAO，可得MK：HK：MH=3:4:5，设 MK=3a，HK=4a，由 M（1，2）可得 H（1+3a，2+4a）由直线 AB

图5

解法4：将MH转化为特殊位置的垂线段NG

如图6，过点 M作MN//AB，交x轴于点N；过点N作NG⊥AB于点G由直线AB解析式为AB，可将直线MN的解析式设为

图6

解法5：通过“折直垂”巧妙转化为最值问题

如图7，过点M作MH⊥AB于点H，连接OH；过点O作OK⊥AB于点K，若以PQ为直径的圆M与AB相切，则OM=MH=2，由于OM+MH≥OH≥OK，而OK=4.8＞OM+MH=2矛盾，所以d＞r，直线AB与圆相离。

图7

当然，本题也可以用垂直的两条直线斜率互为负倒数来解决，但由于超出了初中数学课程标准的要求，这里就不予讨论了。

三、命题思考

1.经典问题，推陈出新，有的放矢，考查素养。

这道期中压轴题以一次函数为背景，推陈出新，图形简洁，题干简约易懂。第3小题集中考查了判断直线与圆的位置关系，直角三角形外接圆的圆心确定方法，点到直线距离的精准作图能力，垂直条件的转化方法，运用基本思想和方法构造基本图形计算垂线段长度等数学的核心概念和内容。在解题的过程中对学生的解题能力和数学素养都提出了很高的要求。

2.一题多解，发散思维，殊途同归，考查能力。

本考题第3小题的设问简洁，言简意赅，学生思路清晰，解法自然生成。判断直线与圆的位置关系，关键要找到圆的半径r和圆心到直线的距离d。由于图中没有d，故第一步就是作d。接着要转化垂直这个条件，方法很多，起到锻炼学生思维的作用。比较常用的有等积转化，构造K型相似等等，针对本题定三角形定直线也可以找到最值等特殊的解法。解法的起点很低，但解题过程中却困难重重，每一种方法都对解题的抽象思维和逻辑推理要求很高，试题的区分度明显。

鬼斧神工的解法，无不以学生分析问题，解决问题的能力为基础，对学生能力的要求尤为突出。这些都给教师平时的教学提出了要求，指明了方向。

四、教学思考

1.要重视对学生数学核心素养的发展。

王尚志教授指出，数学核心素养包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六个方面。数学的学习就是从已知条件出发，对问题进行数学抽象，通过逻辑推理，数学建模，数学运算等等解决问题。在日常的教学过程中，要重视对学生数学核心素养的发展，一切以学生的发展为中心，以生为本，培养能力。在学习的过程中，要帮助学生养成良好的学习习惯。对于数学问题，要帮助学生建立一套研究问题的方法，创造足够的时间和空间，让学生自主探究和创造。

2.要重视对学生“四基”“四能”的培养。

教师在教学的过程中要高度重视基础知识、基本技能、基本思想方法和基本活动经验等内容。在学习的过程中深化对基础知识的理解并逐步迁移，让学生经历知识产生、发展的全过程，培养学生发现问题，提出问题，分析问题和解决问题的能力。试卷中的试题，其本质考查的是学生对书本上的基本概念和基础知识的掌握程度和灵活应用能力，因此不管题目的形式如何改变，但万变不离其宗。要引导学生注意基础知识之间的内在联系和对一些问题通性通法的熟练掌握，重视基本技能和数学思维方法的应用。本题我任教的两个班级得分很低充分暴露出学生基础不扎实和分析问题、解决问题能力不足的短板。

3.要重视对经典问题的回顾和反思。

这道试题给了我们很多的教学启示，比如，要重视对经典问题的回顾和反思。平时常考的一些问题，要让学生自己归纳总结。类似的问题，要让学生总结题目的条件会有哪几种形式，题目的问题有哪些常见的提问角度，解答的方法具体有哪些，最优化的解答如何选择等等。培养学生自己悟数学，将知识点连成线，线再连成片织成一张网，在不断的回顾和反思的过程中提升能力，发展素养。

4.要重视基本图形的研究。

所谓基本图形就是将在“图形与几何”领域的学习过程中具有一定典型性的概念、公式、定理、例题、习题中反复出现、经常用到的对应图形，是结论化的图形，是图形化的公式。借助基本图形，可以使得复杂问题简单化，有利于提高学生的几何直观能力。

例如，对于垂直条件的转化，转化为K型相似是一种方法。研究的过程，教师可以引导学生从图形本身开始研究，慢慢进行变式和变形，最后实现升华，让学生根据图形特征创造性的自主建构基本图形，最后通过总结条件和构图步骤等将知识点内化，积累数学基本活动经验。在遇到例如图8的垂直问题时，学生就会创造性的建立图9或图10，利用相似转化垂直条件了。

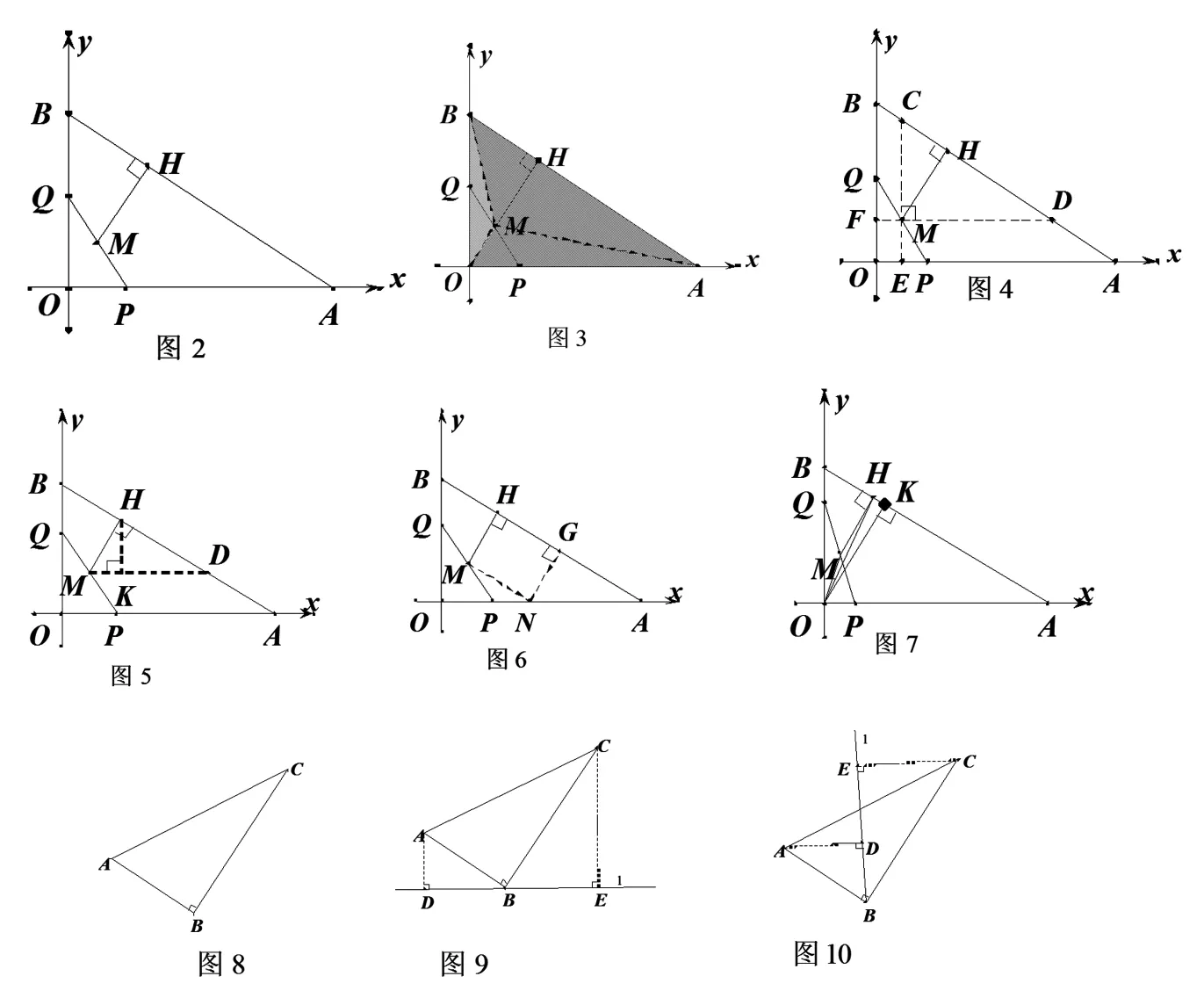
图8

图9

图10

在平时的教学中要重视引导学生分析条件，联想基本图形。有了基本图形的积累，学生能够在它们的指引下主动探索，创造性的添加辅助线，发现解题思路，并解决问题。对基本图形的研究，不仅仅是为发现了多少新的规律和结论，更为重要的是掌握图形研究的步骤、方式方法和途径，以及通过研究图形不断的提高图形研究意识、形成图形研究能力，提升数学素养。