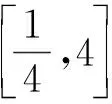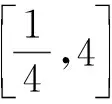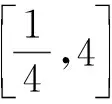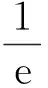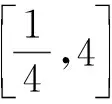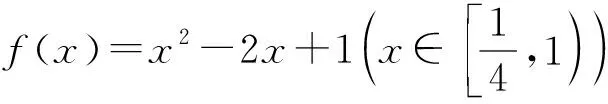提升数学读题能力的几个途径
赵士元
(苏州市吴中区教学与教育科学研究室 215100)
我们经常会听到老师们的抱怨:明明讲课时学生都听懂了,可学生做练习时常常会出错.从平时的课堂观察和学情分析来看,这种现象的确并非个案,或许每一个数学教师都曾有过这样的经历,也为此想了很多法子,有些教师经过思考形成了行之有效的解决之道,而有些教师却一直在寻求答案的路上苦苦探索.作者认为产生这种现象是正常的,从客观来看,数学教学的主要目的并非教会学生一个公式、一条公理、一套解法,而是以数学教材为载体,通过数学课堂让学生学会一种思考——会用数学的方法思考问题,因此数学教学不能满足于学生听懂;从主观来看,许多教师出于“功利主义”的目的,课堂上往往采用大容量、高密度的教学方式,剥夺了学生正常思考的权利,特别是在数学问题的审题方面,许多教师舍不得花足够的时间让学生仔细读题、用心反思,造成了学生的学习机械死板.如何有效克服这种现象?本文试图以读题为话题,谈谈如何提升学生数学审题能力,如何通过反思,强化学生的严密思维,从而提升数学教学效率.
1 让学生在品味中提升读题能力
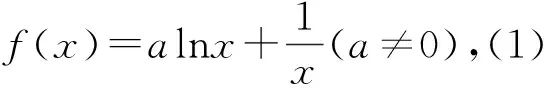

我们知道:求函数的切线方程有两种基本类型:一是已知切点(x0,f(x0)),这时可先求出切点处的导数(即切线斜率),再直接代入切线方程y-f(x0)=f′(x0)(x-x0),这时求出的切线通常只有一条;另一种类型是没有明确切点是哪一点,这时通常设切点为(x0,y0),再写出切线方程y-f(x0)=f′(x0)(x-x0),再利用切线方程的某些已知特征代入方程求出待定参数x0.
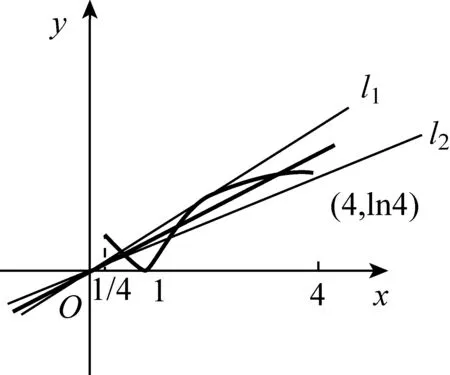
当学生明确切线求法时,再让学生思考“存在两条”的含义其实就是“求出满足条件的切线有两条”,也就是说求出的x0有两个,这隐隐约约让我们感觉到这很可能与方程的根的个数问题有关,这是一个什么样的方程呢?阅读题目的题干,这两条切线的斜率均是a,因此这个方程实际上就是f′(x)=a.是否如此?试试再说.
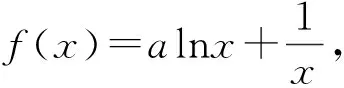
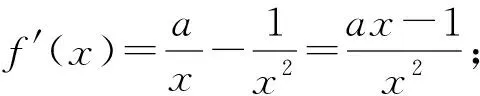
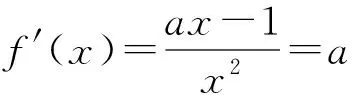
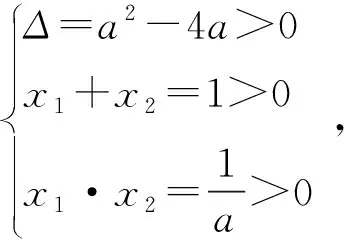

设这两个切点分别为
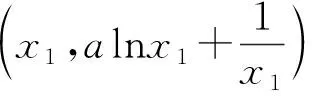
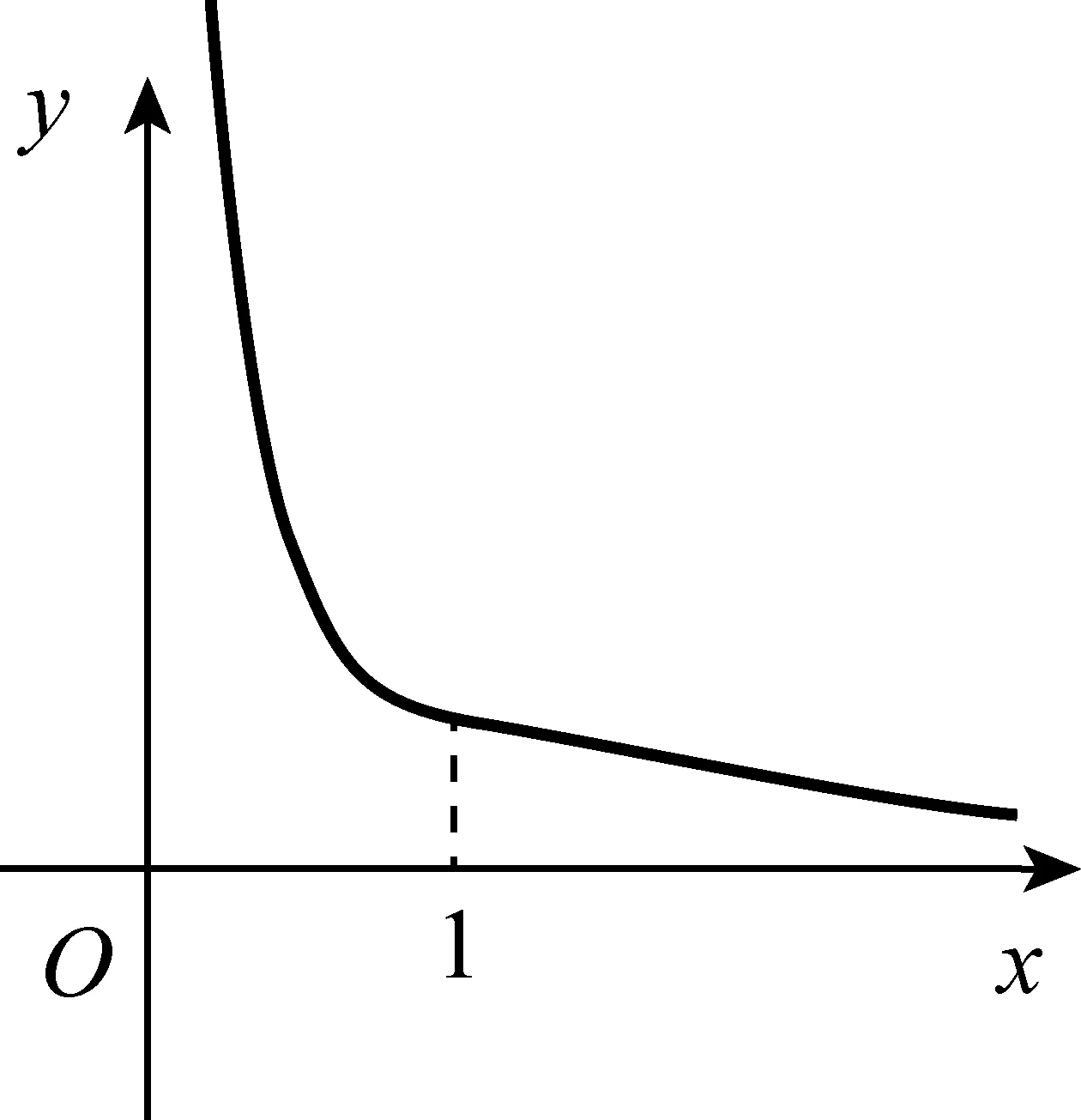
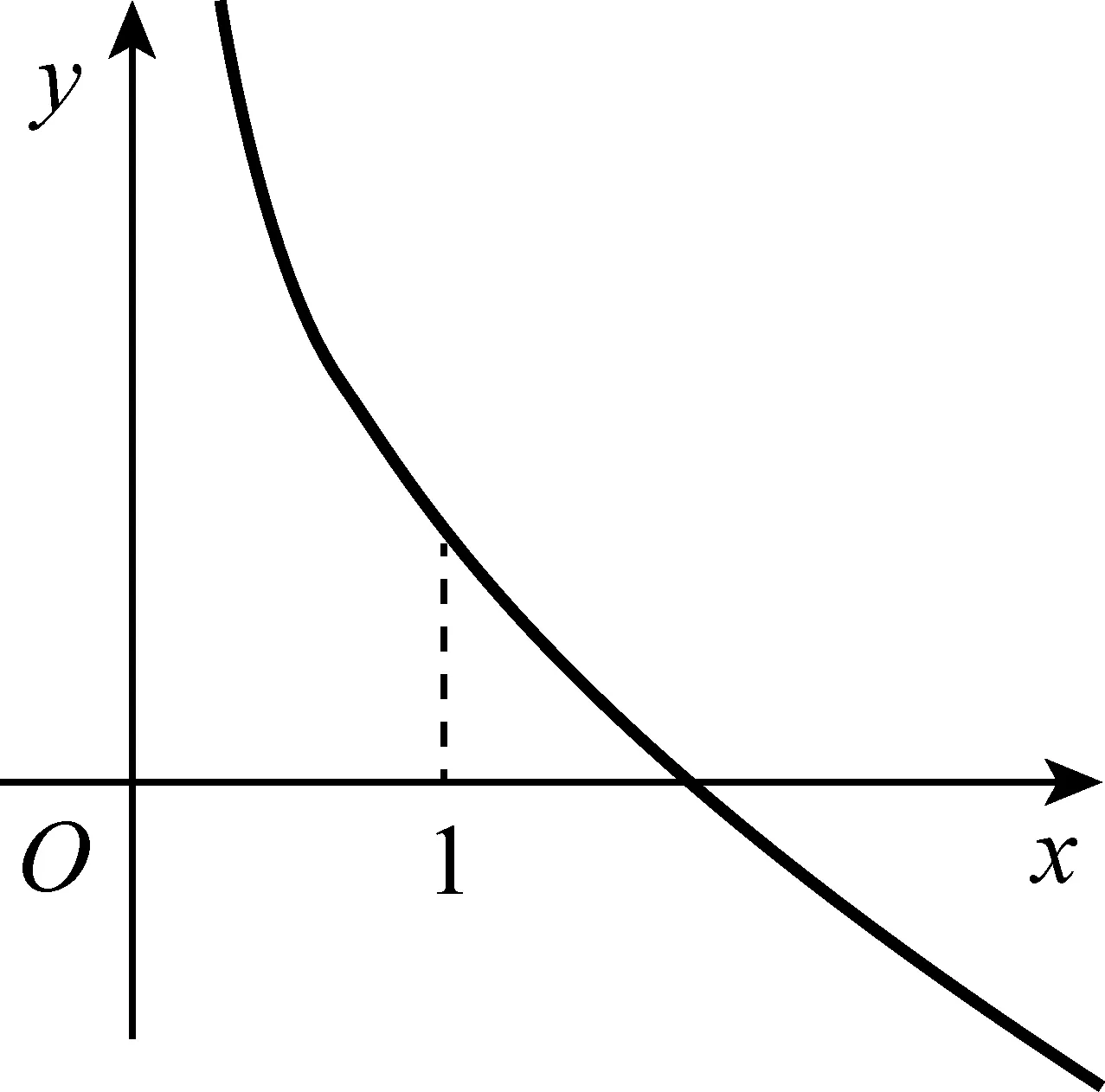
其中x1,x2是方程ax2-ax+1=0的两个不同正根且x1 因为x1,x2是方程ax2-ax+1=0的两根, 所以ax2-ax+1=a(x-x1)(x-x2), 于是当x∈(x1,x2)时, 由此可知,a>4即是我们要求的取值范围. 感悟之一学生的数学审题能力是在不断的训练中逐渐提升的,而在审题过程中吃透并领会题中信息,在逐字逐句的品味中培养学生的题感,不断提升学生的数学读题能力. 在上述案例的第(2)小题时中,有部分学生对条件“{x|f(x)≤0}⊆(0,1)”不能很好地理解而无法找到合适的思路,甚至无从下手.事实上,这一条件用数学语言理解即为“不等式f(x)≤0的解集是区间(0,1)的子集”,于是可以将问题分解两个小问题加以研究: (i)求不等式f(x)≤0的解集A;(ii)若A⊆(0,1),求a的取值范围. 反思之二当证明出函数y=f(x)在区间(0,1)单调递减且f(1)=1时,我们可以断定对任意的x∈(0,1)均有f(x)>0,此时很有可能直接舍去“a<0”这一情况,事实上“对任意的x∈(0,1)均有f(x)>0”仍有两种基本情况,如果f(x)≤0的解集是空集,那么结论仍然成立,此时应保留“a<0”的情况(如图1),若f(x)≤0的解集不是空集,则就应舍去“a<0”的情况(如图2),为说明f(x)≤0的解集不是空集,我们采取选择特殊值的方法(也就是求出f(x)≤0的某一个解),这一点往往会被我们的解题者所忽视,而取特殊值也是数学证明的基本策略. 图1 图2 综上所述:所求实数a的取值范围为a>0. 反思之四从上述反思可以看到{x|f(x)≤0}⊆(0,1)的含义是“不等式f(x)≤0的解集是(0,1)的子集”,用直观语言来理解就是满足不等式f(x)≤0的任意一个x都在区间(0,1)内,这句话是否可以用“不在区间(0,1)内的任意一个x都不满足f(x)≤0”这句话来理解呢?事实上,这两者是等价的,又考虑到函数f(x)的定义域为(0,+∞),于是问题可等价转化为“对任意x∈[1,+∞),都有f(x)>0”,于是我们又产生了如下想法: {x|f(x)≤0}⊆(0,1)等价于“对任意x∈[1,+∞),都有f(x)>0”, 若x=1,则f(x)=1成立; 综上所述:所求实数a的取值范围为a>0. 感悟之二一个数学问题往往是若干个小问题的综合,在教学过程中教师要引导学生学会“解剖麻雀”,将一个综合问题分解为若干个小问题,而后逐个击破.这是解决数学综合问题常常采用的方式策略,也是数学题意理解的基本组成部份. 感悟之三许多同学把精力集中在不等式f(x)≤0求解上,如果我们的思路只局限于这一点,那么解题就显得力不从心了.此时,应当引导学生逐步理解题干条件中所隐含的丰富信息,引导学生多读题、多思考,不必担心思考和读题的时间影响解决问题的进程.当学生习惯了这种思考和读题后,他的数学理解能力和思考能力会得到不断提升,有利于增强他们的问题意识、提高其解决问题的能力,这就是“磨刀不误砍柴功”在数学学习的体现. 从阅读量来看,该题共有230多字的阅读量,比较适合高二学生,但是题中数字较多,而且题中“当且仅当”的数学语言让部份学生“犯难”,学生要么对“当且仅当”这样的数学语言理解不清,不会用生活化的语言来理解,要么无法将此问题与数列的最大最小项问题联系起来,因此出现了许多本不应该出现的错误. 感悟之四本案例初看是一个函数最值问题,但由于函数定义域是正整数集,于是把函数最值问题转化为数列最值问题,通过转换“视角”在“山重水复疑无路”的情况下达到“柳暗花明又一村”的效果.换个角度思考问题实际上也是数学问题解决过程中常常被采用的策略. 在数学学习过程中,常常会出现一些问题,这些问题在教师看来似乎很易理解,但由于受生活经历和理解能力所限,学生往往一时无法理解透彻,因此在学习过程中往往会“死记硬背”,这时教师会误以为学生已听懂甚至学会,但学生在实际演练时又会出现这样那样的错误,其根本原因是教师在教学过程中不善于用通俗易懂的方法帮助学生理解从而导致学生的学习只停留在浅层次的学习状态中. 案例三“不等式恒成立”、“不等式能成立”、“不等式无解”问题常常是学生学习过程中的一个难点,大多数学生只是生硬地记住了“不等式f(x) 有这样一个问题:已知函数f(x)=x2-2x+3. (1)若对∀x∈[-1,4]不等式f(x) (2)若存在x∈[-1,4]使不等式f(x) (3)若不等式f(x) 教学时这一内容时是这样处理的:首先,当自变量x在一定范围内取值时,对应的函数值y在某一范围变化,它的不同取值形成一个集合(这个集合实际上就是函数的值域),而“f(x) 通过这一通俗化的比较,学生很容易理解“不等式f(x) 为了让学生能较好地理解第(2)问,又提出了一个生活化的问题:在我们班里存在一个学生,年纪比老师小,是否有必要逐个验证?如果不需要这么做,我们又该怎么处理?经过短暂的思考,很多学生都能完美地回答出“只要我们班级里最小的学生比老师小就可以了”,随后立即追问:“存在x∈[-1,4]使不等式f(x) 第(3)个问题实际上可以转化为类似于(1)的情况,为了让学生理解题意,读懂题目,老师用通俗语言替代数学语言帮助学生理解,提出了如下一系列问题: 你能用通俗的语言来表达“不等式f(x) 这句话的意思是否可以等价地转换成“不等式恒成立问题”? 事实上,“不等式f(x) 当然,处理这类问题时我们还可以采用“补集思想”,即先研究不等式f(x) 感悟之五数学语言往往是比较抽象的,当学生无法理解抽象的数学语言时采用通俗化的生活语言帮助学生理解题意,不仅有利于提升学生的数学学科素养也有利于在不断的转化过程逐步提升学生的数学审题能力.特别是在数学概念教学和处理一些陌生问题时更显有效而且较易被学生接受.但要让学生能比较自然地用通俗易懂的生活语言理解数学概念及数学问题,从而将枯燥乏味的数学概念或数学公式转化为生动幽默的生活语言,这需要教师具有较高的语言素养和语言运用能力. 在分析案例三的第(3)个小问题时我们提到了“补集思想”,在案例1中我们提到了“逆向思考”,这些都是“逆向设问”的一种,有时“逆向设问”可以将一个陌生的问题转化为一个熟悉的问题,教学过程中如若经常采用这种“逆向设问”的方式进行教学,学生的学科能力和数学阅读能力便会在这种问题情景下不断提升. 感悟之六“逆向设问”的目的与“换位联想”类似,它们都是为了“陌生问题熟悉化”,而“将未知转化为已知”、“将陌生转化为熟悉”都是数学学习过程中必须掌握的转换技巧,让学生学会多角度思考问题、多方位转换问题,学会全路径探讨问题,最终实现学科素养和学科的提升是数学教学的目的,也是培养学生数学阅读能力的基本手段.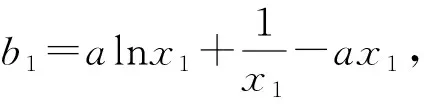
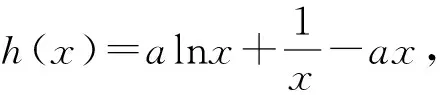
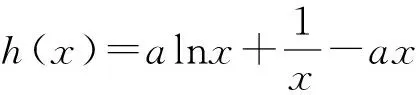
2 让学生在细微处提升读题能力
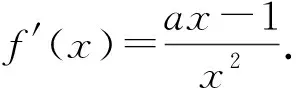
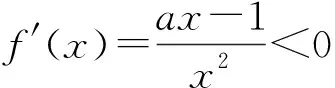
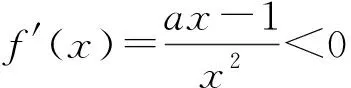

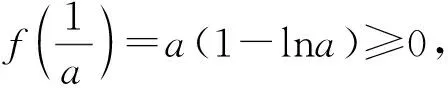
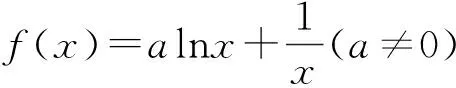
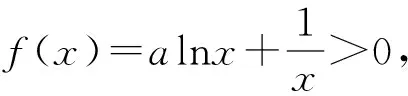
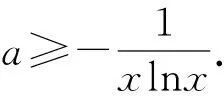
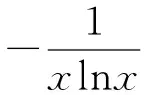
3 让学生在思辩中提升读题能力

4 让学生在比较中提升读题能力
5 让学生在问题探索中提升读题能力