近三年中考“尺规作图”命题分析、感悟及实践
肖世兵


1 命题趋势分析
为了了解中考对“尺规作图”的考查情况。本次调查采用点面结合的调查方式。既对全国进行面上的数量统计。又以江苏省为例对省内各大市进行点上的调查。同时。本次分析采用定量与定性相结合的分析方法。
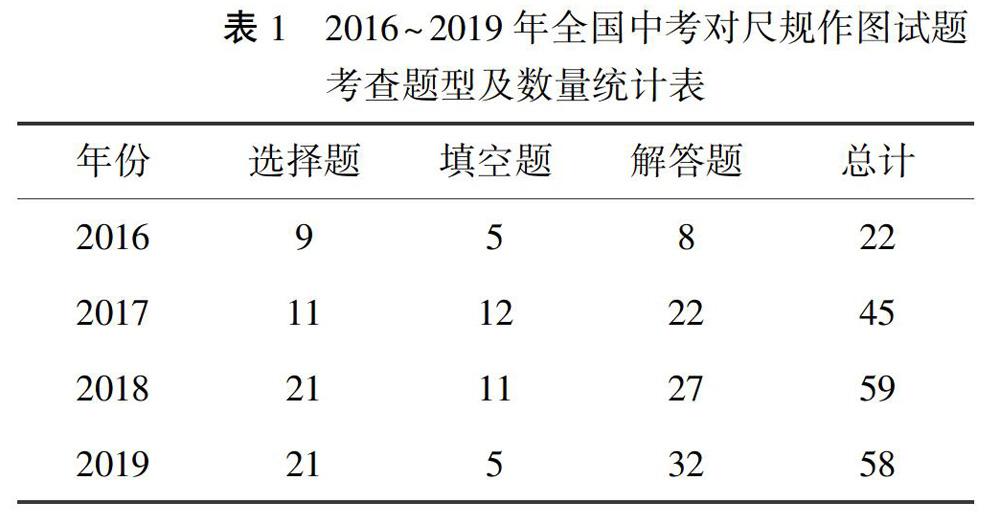
从考题数量来看,2016年仅有22题,占比极低;2017年题量较2016年相比翻了一番;2017-2019年尺规作图题在全国中考所占比重呈逐年上升趋势。其中2018年和2019年相对稳定。
表2是江苏省近三年十三大市在尺规作图方面考查的情况。从表2可知。江苏省各市对尺规作图题的考查仍存在很大的差异,南京、无锡近三年一直关注尺规作图的考查,且题型以解答题居多,所占分值较大。部分地区一直未进行尺规作图的考查。
综上可见,尺规作图的考查,近几年虽有所加强,但仍存在地区差异较大。
2命题思路分析
通过对近三年的中考尺规作图的试题分析。根据考查内容,将试题考查分为三类:隐含式考查、补图式考查、应用式考查。
2.1 隐含式考查
所谓隐含式考查。是命题者通过借用作图痕迹、作图语言隐含地传递、表达题目的已知条件。此种呈现方式,让几何试题旧貌换新颜,令人耳目一新。
案例1(2019宜昌)通过如下尺规作图,能确定点D是BC边中点的是()。
本题通过作图痕迹来传递题目所包含的已知条件信息,符合《课程标准》中“保留作图的痕迹,不要求写出作法”的目标要求,主要考查对基本作图的作法痕迹的了解。
2.2 补图式考查
所谓补图式考查。是命题者将尺规作图嫁接在几何题上。即给出部分几何图形,考生需要先根据作图要求。补全图形。然后再解答问题。
(2)探究OE与AC的位置及数量关系,并证明你的结论
本题尺规作图主要考查了角平分线的作法。此种命题方式常见于解答题,主要考查基本作图的作法。但此考法存在的弊端是不利于阅卷,阅卷时难以分辨作图的真假,从作图痕迹看存在不少“伪作图”的现象,这或许是命题者放弃尺规作图考查的因素之一。
2.3 应用式考查
所谓应用式考查。是需要考生综合运用几何图形性质、判定等知识。凭借几何直观、逻辑推理等几何素养。解决问题。
本题给出作法,主要考查作法依据。此种题型,对作图原理的考查要求较高,很好体现《课程标准》中“了解作图的道理”的目标要求。有利于培养学生“知原理。重探究”的科学理性精神。
(1)问,抓住图形的轴对称性,利用几何直观,很容易想到“延长BA,CA交半圆于点E,F”的作法。(2)问。首先从“45°的圆周角”进行推理得出“所求作的点应是半圆的中点”,其次,如何找到半圆的中点?同样,借助于图形的轴对称性,推理出所求作的点也在对称轴上。问题再次被转化为“求作此图的对称轴”。
此类题型,综合性强,灵活,难度较大,具有创新性。这种应用型的作图也体现了对几何直观、逻辑推理等核心素养的考查,是尺规作图中的亮点试题,也是尺规作图教学的价值取向。
3 感悟及命题实践
尺规作图有着独特的教学价值,尺规作图教学在培养学生严谨的学习习惯、严密的逻辑思维、渗透图形变换思想、渗透数学文化等方面发挥重要作用。尺规作图对学生所学的相关知识及新知识结构起着固本作用,作图是思维实验与动手实验的合拍,是逻辑推理与合情推理的牵手,是几何学习的有力助手,它扎根几何原理,关乎思维发展,连接着图形变换,是实现图形运动的强有力手段。当然。尺规作图在核心素养的培养上也是举足轻重的。
尺规作图如此重要,但在现实教学中,却遭遇了冰火兩重天的尴尬境界。究其原因,一方面。课改初期尺规作图的删减造成的后遗症,即使《课程标准》和教材做了调整。但也收效甚微。另一方面。在教育功利化的驱动下,考什么教什么,不考则不教或少教的指导思想一直占主流。比如。南京中考2017~2019年连续三年考查了尺规作图。随之而变的是南京2019年各地区八年级第一学期的期末试卷中无一例外的也都考查了尺规作图。风向变速之快。扬州中考二十几年没有考查尺规作图了,结果是什么,大家可想而知,由此可见。考试对教学的影响非同一般。
教学评的一致性。让笔者意识到对于尺规作图既要重视教学,也要重视考查。因此,笔者借助区级期末命题工作,发挥考试的导向功能,旨在引导大家重视尺规作图。以下是笔者关于尺规作图的命题实践。
(2)结合补完整的图形,判断PA和PB有什么数量关系和位置关系?并说明理由。
命制意图 本题属于补图式考查,(1)问重点考查本学期所学习的角平分线、线段垂直平分线的尺规作图,(2)问重点考查了逻辑推理的能力。
案例7(2017-2018年江都区九年级第一学期期末卷第26题)由边长相等的小正方形组成的网格,以下各图中,点A,B,C,D都在格点上。
(1)在图7中,PC:PB=___;
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法。
①如图8,在AB上找点P,使得AP:PB=1:3;
②如图9,在BC上找点P,使得△APB~△DPC;
③如图10,在△ABC内找一点P,连接PA,PB,PC。将△ABC分成面积相等的三部分。
命制意图 尺规作图是数学文化长廊中一颗耀眼的明珠。它以直观呈现的方式展示图形的视角美和内涵美。尺规作图能反映学生数学思维的灵动性和创造性,能够反映学生的数学基本活动经验、实践能力和创新意识等核心素养。在过去很长一段时间内。因为平时作业中根本不用画几何图。考试中几乎不考作图,所以许多一线教师忽略尺规作图的教学,忽视尺规作图的重要性,学生作图能力普遍偏低。因此,笔者想借此次全区的统测机会,发挥试题对教学的导向功能,引导教师关注课标,关注尺规作图,关注对学生作图能力的培养。
一点的作文论述,一贯的命题坚守。旨在呼唤大家关注尺规作图的价值,重视尺规作图的教学,发挥尺规作图在培养学生学习习惯、几何素养、探究精神等方面的作用。让尺规作图。这一珍贵的教学“食材”,烹制出一席营养丰盛的教育大餐!让尺规作图的文化精髓,越发光采奕奕。越发生机勃勃!

