基于MPC导引律的AUV路径跟踪和避障控制

姚绪梁，王晓伟，2，*

（1.哈尔滨工程大学 自动化学院，哈尔滨150001； 2.九江职业技术学院 机械工程学院，九江332007）

自主水下航行器（AUV）在海洋科学、水下勘探、搜索和救援、海底管道跟踪、海底电缆维护和国防等领域得到广泛的应用。路径跟踪是AUV完成各种作业任务的关键技术。为了简化路径规划和降低计算量，AUV的路径经常基于路径点进行规划，路径点之间用直线进行连接。所以，对直线路径进行跟踪是AUV一项非常基本的控制任务。但是，AUV动力学模型存在非线性、耦合性和不确定性。另外，为了节能、降低成本和提高可靠性，大部分AUV都被设计为欠驱动的形式，在某些自由度（例如：横向和垂向）缺少驱动能力，以上原因导致AUV的路径跟踪控制变得非常棘手。

针对路径跟踪的导引律问题，国内外进行了大量的研究。文献［1］应用视线法（LOS）导引律来镇定横向跟踪误差，然后应用反馈线性化方法设计了动力学控制器，实现了欠驱动水面船舶直线路径跟踪控制，但没有考虑模型的不确定性。为了改善路径跟踪的效果，文献［2］设计了一种前视距离时变的LOS导引律。文献［3］针对无人水面艇的路径跟踪控制，应用积分视线法（ILOS）导引律，并采用反馈线性化方法设计了航速和航向的动力学控制器。另外，文献［4］针对欠驱动水面船舶的路径跟踪控制设计了一种向量场（VF）导引律。针对AUV动力学模型的非线性、耦合性和不确定性，动力学控制的设计也得到了广泛的研究。目前，常用的方法有PID控制［5］、反馈线性化控制［6］、自适应控制［7］、鲁棒控制［8］、滑模控制（SMC）［9］、模糊控制［10］和神经网络控制［11］等。但是以上文献都没有考虑实际控制输入的约束问题。文献［12］考虑了输入的约束，应用模型预测控制（MPC）对LOS导引律进行优化，改善了船舶对直线路径的跟踪质量。文献［13］考虑了舵角的幅值和速度约束，应用MPC设计控制器实现了AUV的纵倾和深度控制。但是文献［12-13］都是基于名义模型，没有考虑模型的不确定性。基于路径点的直线跟踪控制虽然路径规划简单便于应用，但是路径在路径点处是不光滑的。在AUV对路径进行跟踪过程中，当路径在路径点附近进行切换时，跟踪误差会存在突变，从而使舵角很容易产生饱和。舵角频繁出现饱和不仅会降低系统的稳定性，而且还会增加AUV的阻力和能耗。文献［14］针对船舶的路径跟踪控制，考虑了舵角的饱和并应用反步法设计了控制器，但并没有从根本上改善舵角的饱和现象。另外，在路径跟踪过程中，经常需要避障，设计避障导引律［15］和对路径进行重新规划［16］是目前常用的避障方法，但是这2种方法都会增加控制器的复杂度。

本文针对欠驱动AUV三维直线路径跟踪和避障控制，基于级联控制理论设计了运动学和动力学控制器。在运动学控制器中考虑了AUV角速度存在的约束，应用MPC设计了导引律，负责产生期望的角速度信号。为了实现对期望速度信号的跟踪，在动力学控制中考虑了推进器转速和舵角的饱和，应用SMC设计了动力学控制器，可以有效地克服模型的不确定性，保证系统的鲁棒性。

1 欠驱动AUV运动模型

本文研究的欠驱动AUV在尾部配置一个推进器用来实现对纵向速度的控制、水平舵和方向舵分别实现对纵倾和艏摇的控制，在横向和垂向没有驱动力。图1为欠驱动AUV三维直线路径跟踪示意图，｛B｝：O-xyz和｛I｝：E-ξηζ分别为随体坐标系和固定坐标系；φ和p分别为横摇角和横摇角速度；Rk为接受圆半径。因为存在恢复力，AUV的横摇很小，另外路径跟踪不需要对横摇进行控制，忽略横摇后，AUV的运动学模型可以简化为如下五自由度的形式：

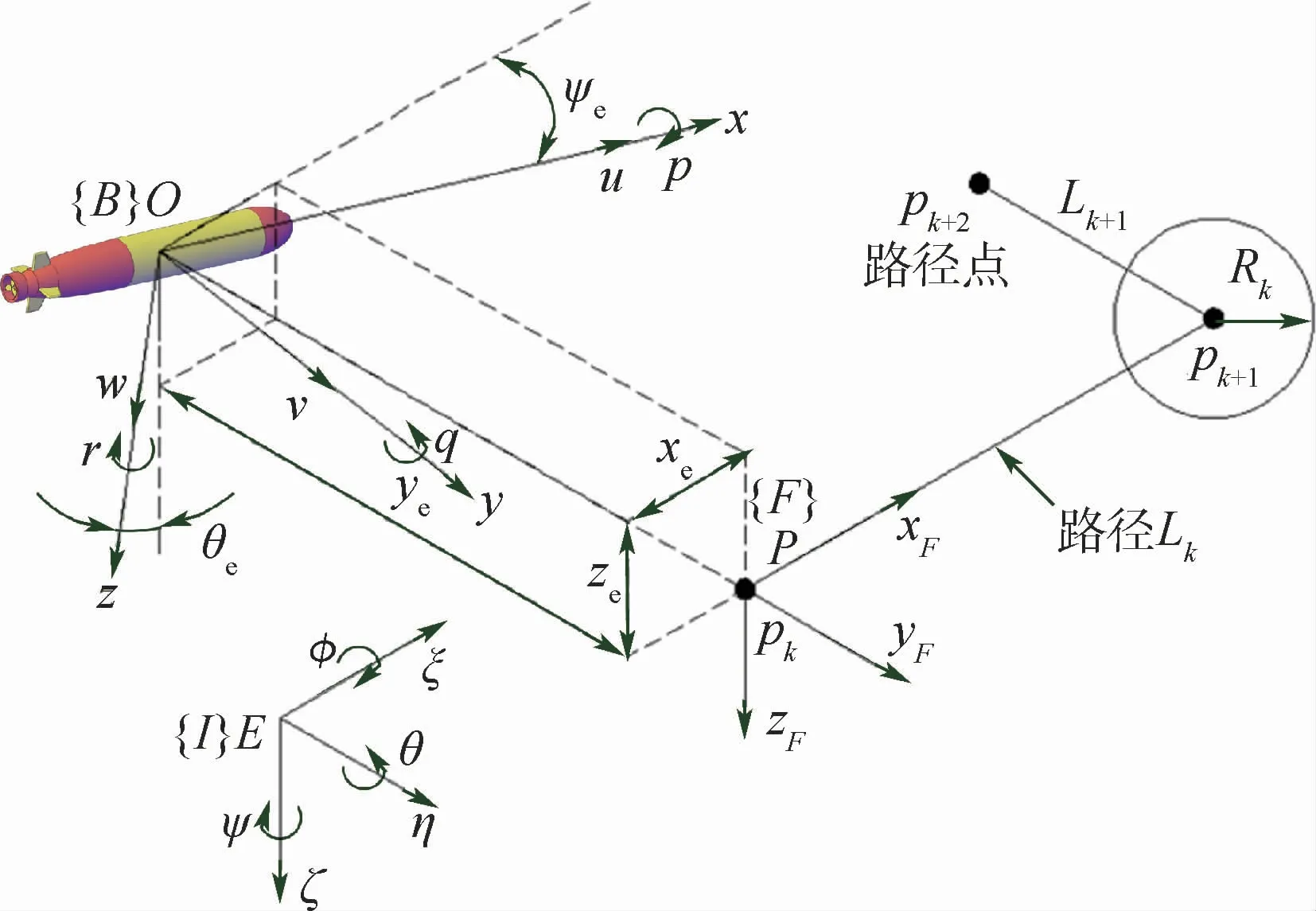
图1 欠驱动AUV三维直线路径跟踪示意图Fig.1 Schematic diagram of underactuated AUV 3D straight path following

式中：η＝［ξ η ζ θ ψ］T表示AUV在固定坐标系｛I｝中的位置和姿态，（ξ，η，ζ）为AUV在｛I｝中的坐标，θ和ψ分别为纵倾角和艏摇角；v＝［u v w q r］T表示AUV在随体坐标系｛B｝中的速度分量，u、v、w、q、r分别为纵向、横向、垂向速度和纵倾、艏摇角速度。J（η）为｛B｝到｛I｝的旋转变换矩阵，表达式为

2 三维直线路径跟踪误差模型

为了便于建立路径跟踪误差模型，以当前直线路径的起点pk为原点定义坐标系｛F｝：PxFyFzF。｛F｝坐标系的xF轴与直线路径重合并指向下一个路径点pk+1，yF轴指向右侧，zF轴指向下方。定义｛F｝坐标系相对于｛I｝坐标系的姿态为AF＝［θFψF］T，其计算公式为

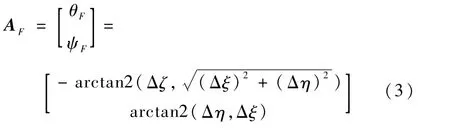
式中：Δξ＝ξk+1-ξk，Δη＝ηk+1-ηk，Δζ＝ζk+1-ζk；（ξkηkζk），（ξk+1ηk+1ζk+1）分别为当前直线路径起点pk和终点pk+1在｛I｝坐标系中的坐标。定义AUV相对于｛I｝坐标系的姿态为AB＝［θ ψ］T，则AUV相对于｛F｝坐标系的姿态误差计算如下：

式中：下标e表示误差。

对式（4）求导可得

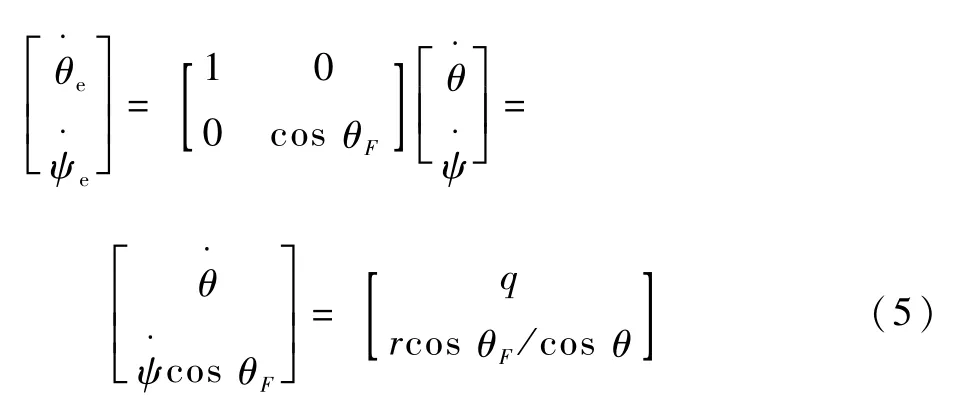
定义AUV在｛I｝坐标系中的坐标PO＝［ξo，ηo，ζo］T，P在｛I｝坐标系中的坐标PP＝［ξk，ηk，ζk］T，则AUV相对于｛F｝坐标系的位置误差为

对式（6）求导可得

3 三维直线路径跟踪控制器的设计

控制器分为运动学和动力学控制器两部分，首先在运动学控制器中应用MPC设计了导引律，负责产生期望的纵倾角速度qd和艏摇角速度rd。然后，应用SMC设计了动力学控制器，负责产生实际的控制信号，即推进器的转速np、水平舵角δs和方向舵角δr。

3.1 运动学控制器

因为动力学控制器对期望速度信号的响应有一定的延时，为了减小延时对控制效果的影响，添加如下低通滤波器：

式中：T1＞0、T2＞0为可调时间常数。

因为本文研究的欠驱动AUV在横向和垂向没有驱动力，所以v和w是非常小的，为了简化控制器设计，可对其进行忽略。另外，纵向误差xe不需要进行控制。根据式（5）、式（7）和式（8），三维直线跟踪可简化为以下系统的镇定控制问题：

其中：T为采样周期。

根据预测模型（11），未来的状态变量可以通过式（12）进行预测：

输出量可以重新整理为如下矩阵形式：

式中：

考虑控制量的幅值存在如下约束：

通过用Uk，k参数化，可以将约束（15）整理为如下线性不等式的形式：

取上一采样时刻最优解Uk-1，k-1的后Nc-1个控制增量和当前时刻最优解Uk，k的最后一个控制增量组成一个当前时刻的可行解，该可行解及在其控制作用下的预测输出分别为

定义ΔJk，k＝Jk，k-Jk-1，k-1，则

所以只要满足约束条件（19）则可以保证ΔJk，k≤0，从而保证MPC的稳定：

因为式（20）等号右边第1项为常量，所以MPC每一步的优化问题等价为求解如下约束问题：

通过对式（21）求解可以得到预测时域内的控制量Uk，k，将Uk，k的第1个值uk，k代入式（22），即可得到当前采样时刻纵倾和艏摇角速度的最优期望值为

3.2 动力学控制器

因为本文研究的欠驱动AUV在横向和垂向没有驱动力，所以其横向速度v和垂向速度w是非常小的，为了简化动力学控制器的设计，可以将动力学方程进一步简化为

式中：

因为推进器的推力和舵力是具有饱和限制的，定义输入饱和量为

为了对输入饱和进行补偿，设计如下辅助系统：

式中：

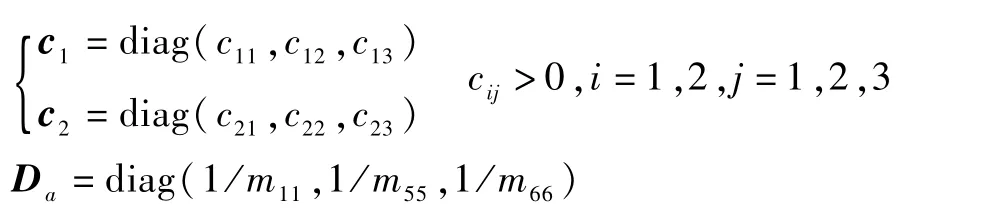
定义误差变量：

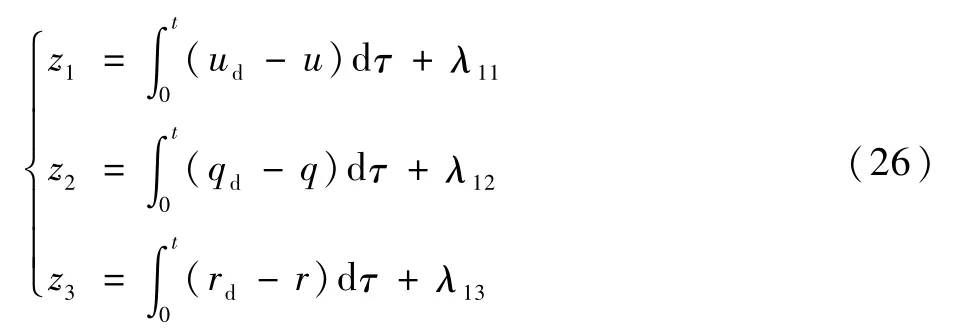
式中：ud＞0为期望的航速。

定义滑模函数：

因为AUV的期望航速ud被设置为常值，所以系统可以近似为自治的，可以认为du、dq、dr有界且慢时变，其导数可以忽略。定义误差变量：

定义Lyapunov函数：

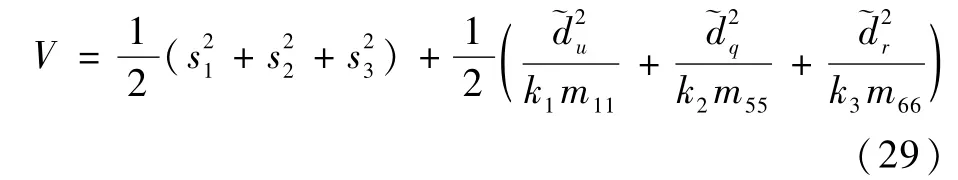
对V求导可得

设计控制律和自适应律为

式中：ρ、KT、DP、kL分别为流体密度、螺旋桨推力系数、螺旋桨直径、舵的升力系数。

4 仿真结果与分析

本文采用REMUS-100作为仿真模型，模型参数可以参考文献［17-18］。仿真采用了2种控制方法进行了对比。

1）方法1

采用本文所设计的控制器，控制器的主要设计参数为：T＝0.1，T1＝0.5，T2＝0.5，Q11＝2，Q22＝2，Q33＝2，Q44＝2，Q55＝1，Q66＝1，R11＝2，R22＝2，Np＝10，Nc＝3，k1＝0.1，k2＝0.1，k3＝0.1，k4＝0.1，k5＝0.1，k6＝0.1，k7＝0.2，k8＝30，c11＝1，c12＝1，c13＝1，c21＝1，c22＝1，c23＝1，c31＝1，c32＝1，c33＝1，umax＝［0.15 0.2］T，umin＝［-0.15 -0.2］T。期望直线路径基于表1所列路径点生成。AUV的初始位姿和速度均为零。期望航速ud＝1m/s，路径切换的接受圆半径Rk＝10m。在仿真中设置了一个障碍物，其半径为5m，在固定坐标系中的坐标为：PA＝［ξA，ηA，ζA］T＝［85，0，21］Tm。仿真中选择从右侧避障，惩罚项按式（32）进行设置：

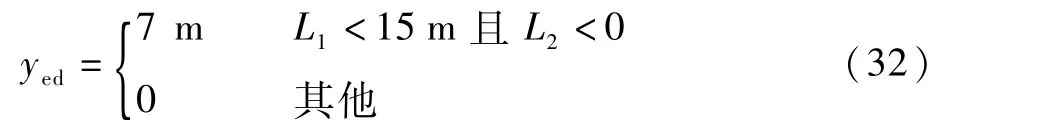
表1 路径点Table 1 Way points m

2）方法2

运动学控制器采用了LOS导引律进行路径跟踪和避障［15］，动力学控制器采用PID控制器。为了验证控制器的鲁棒性，仿真时段0～100 s水动力参数增加20%，100～250 s采用名义水动力参数，250～400 s水动力参数减小20%。

图2 路径跟踪和避障仿真结果Fig.2 Simulation results of path following and obstacle avoidance

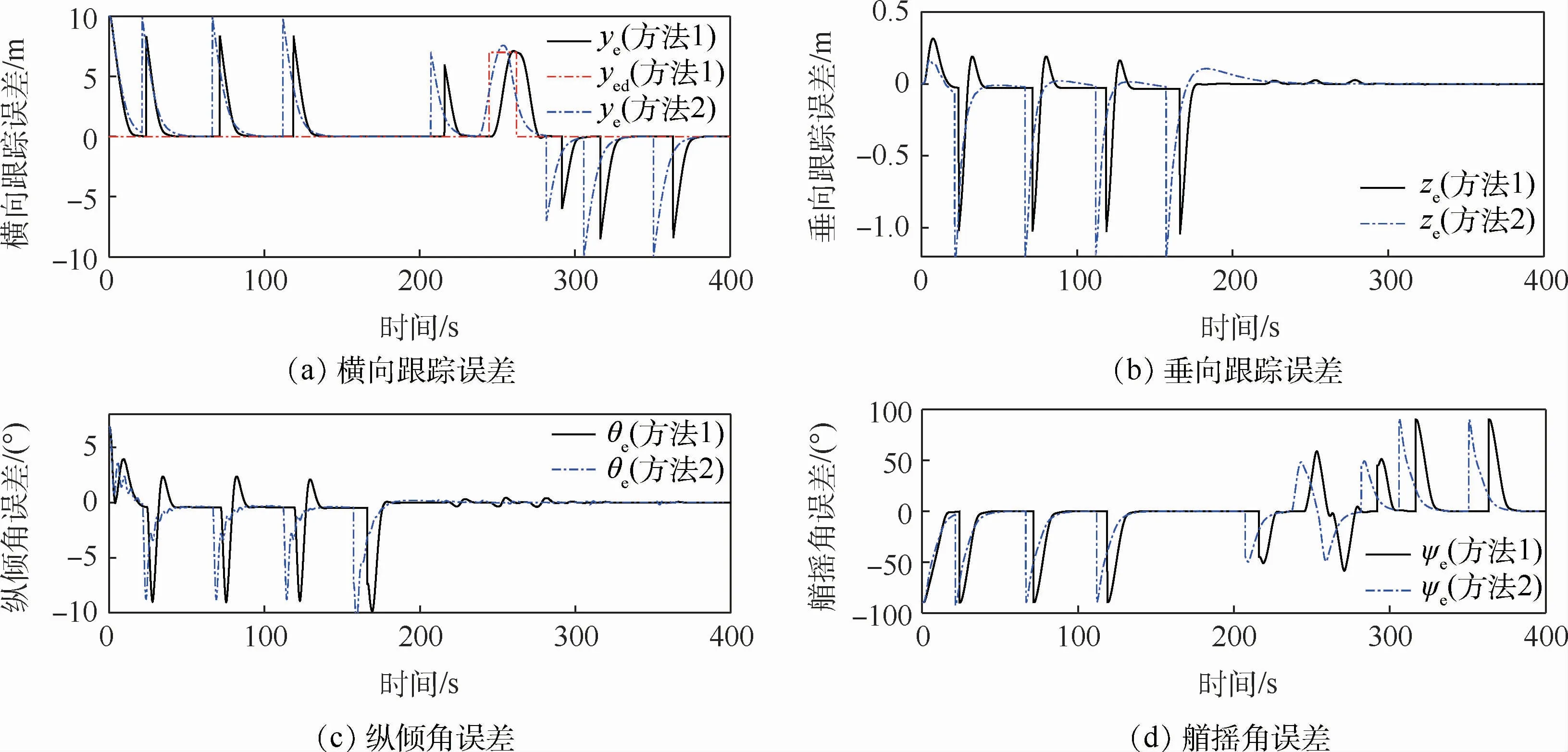
图3 路径跟踪误差曲线Fig.3 Path following error curves

图2为三维直线路径跟踪和避障示意图及其在水平面、垂直面的投影图。可以看到，2种控制方法都能实现对直线路径的跟踪和避障。但是通过对比也可以看到，在每次进行路径切换时，方法1的跟踪效果更好一些，能够更快地收敛到期望路径上，另外方法1能够更快更准确地收敛到期望的横向误差从而更好地完成避障。图3为路径跟踪误差曲线。可以看到，每一段直线路径上的位置误差和姿态误差都能收敛到零，同时可以看到方法1大约在250 s时将yed设置为了7 m，从而启动了避障，当避障完成后yed又被设置为零，最终使AUV重新收敛到期望路径上。图4为实际的控制输入曲线。可以看到，控制输入存在有规律的抖振，其主要原因是直线路径在路径点处不光滑，路径切换时跟踪误差存在跳变。仿真中根据实际情况将舵角的最大绝对值设置为25°，可以看到方法2中的舵角在路径切换时出现了饱和现象，但方法1没有出现饱和现象，整体上方法1的舵角更加平稳，这样更利于系统的稳定性和节能。图5为AUV的速度曲线。可以看到，2种控制方法都能使AUV的纵向速度收敛到期望值，但方法1的控制效果更稳定一些，同时可以看到横向和垂向速度很小而且是收敛的。方法1的纵倾角速度和艏摇角速度都在约束范围之内，从而有效地改善了舵角饱和现象。图6为方法1的鲁棒项系数和滑模函数曲线。可以看到，所有的滑模函数在路径切换时都出现了一定的抖动，但均是收敛的且趋于零，鲁棒项系数能够自动进行调整从而有效地减小鲁棒项引起的抖振。

图4 控制输入曲线Fig.4 Control input curves

图5 速度曲线Fig.5 Speed curves

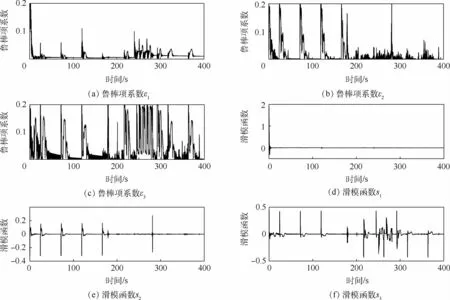
图6 鲁棒项系数和滑模函数曲线Fig.6 Robust term coefficients and sliding mode function curves

5 结 论

1）本文基于级联控制理论分别应用MPC和SMC设计了运动学和动力学控制器，从而实现了欠驱动AUV三维直线路径跟踪和避障控制。

2）在运动学控制器中设计了线性时变MPC导引律，并设计了MPC的稳定约束条件。因为运动学方程不受动力学模型不确定性的影响，所以运动学控制器采用MPC不仅能保证预测的效果，而且可以简化控制器的设计。

3）运动学控制器考虑了期望角速度的约束，可以有效地改善舵角的饱和现象，从而更利于系统的稳定性和节能。

4）动力学控制器采用SMC可以克服动力学模型的不确定性，保证系统的鲁棒性。

接下来将针对存在海浪、海流等环境干扰下的欠驱动AUV三维路径跟踪进行进一步的研究。