基于FRFT的多分量LFM 信号检测与参数估计方法
宋耀辉,黄仰超,张衡阳,秦智康,高维廷
(空军工程大学 信息与导航学院,西安710077)
变换域通信在电磁环境日益复杂、通信干扰样式日益多样化的条件下被提出,其以独特的频谱感知、主动规避干扰频段的通信思想,得到了广泛发展。目前,对多分量线性调频(LFM)干扰信号参数进行准确估计是变换域通信的一个难题,也是影响通信质量的关键因素。在关于LFM 信号检测与参数估计的典型方法中,文献[1-2]通过W-V变换进行参数估计,但是由于该变换的非线性性质,导致运用到多分量信号参数估计时出现交叉项干扰,影响参数估计精度;文献[3-5]将分数阶傅里叶变换(Fractional Fourier Transform,FRFT)与短时傅里叶变换(Short-Time Fourier Transform,STFT)分析方法结合,消除了多分量参数估计时交叉项的干扰,但由于需要选择合适的窗函数,增加了算法的复杂度;文献[6]提出一种低复杂度的参数估计算法,通过不断迭代找到信号的冲击量,但该算法受限于采样频率;文献[7-8]利用分数阶自相关函数寻找峰值,文献[9]减少信号采样点数,文献[10]采用稀疏傅里叶变换,分别从各自角度减小运算复杂度,但都未就具体如何寻找最优旋转角度进行讨论;文献[11]提出一种高效的FRFT算法,可快速准确地估计信号参数,但不适用于多分量LFM信号的情况。
本文提出一种快速准确地检测并估计多分量LFM信号参数的方法。该方法借助FRFT与W-V变换间的旋转等价关系,以及LFM 信号在分数域的功率谱是聚集性优良的直线段特点,推导出不同旋转角度下直线段长度间存在近似线性关系;利用2个初始角度下LFM 信号的时频直线段长度,定位出最优旋转角度的粗略值;再根据LFM信号功率谱幅值随旋转角度的变化规律,以最高效方式搜寻最优旋转角度,并估计信号参数。利用CLEAN思想,逐个搜寻整个频域内所有的LFM信号分量。为提高检测方法的抗噪能力,采用移动窗滤波器,对时域信号进行功率谱平滑去噪,并在变换域求平均,从而更好地获取时频直线段长度。与传统的多分量LFM 信号检测方法相比,本文方法具有较高的精确度和较低的运算复杂度,且抗噪能力强。
1 LFM 信号的分数域分析原理
FRFT是傅里叶变换的扩展形式,是分析频率时变类信号的有力工具。文献[12]推导出FRFT与W-V分布之间的关系如下:
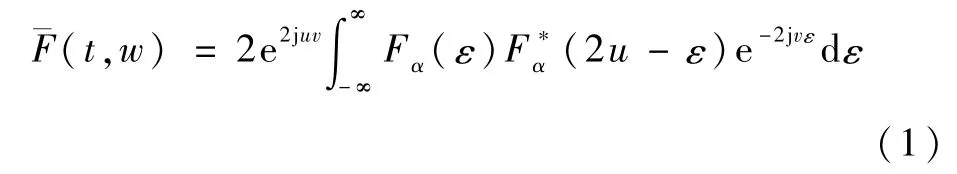
由此可知,FRFT是W-V变换在时频域旋转一定角度得到的,信号在两者的映射中存在密切联系。
在此基础上,文献[11]分析出单分量LFM信号在这2种时频域中映射直线段之间的关系为

式中:Lφ为信号在W-V变换域中的时频线长度;φ为W-V变换的时频线角度;Lα为分数阶长度;α为分数阶傅里叶变换旋转角度。
假设某单分量LFM信号为

式中:A为信号幅度;f0为初始频率;k为调频系数。
对该信号进行不同旋转角度的FRFT变换,得到函数图像如图1所示。
分别用Lα1、Lα2表示信号在旋转角度α1、α2的分数域直线段长度,不妨设α-φ>0,可得
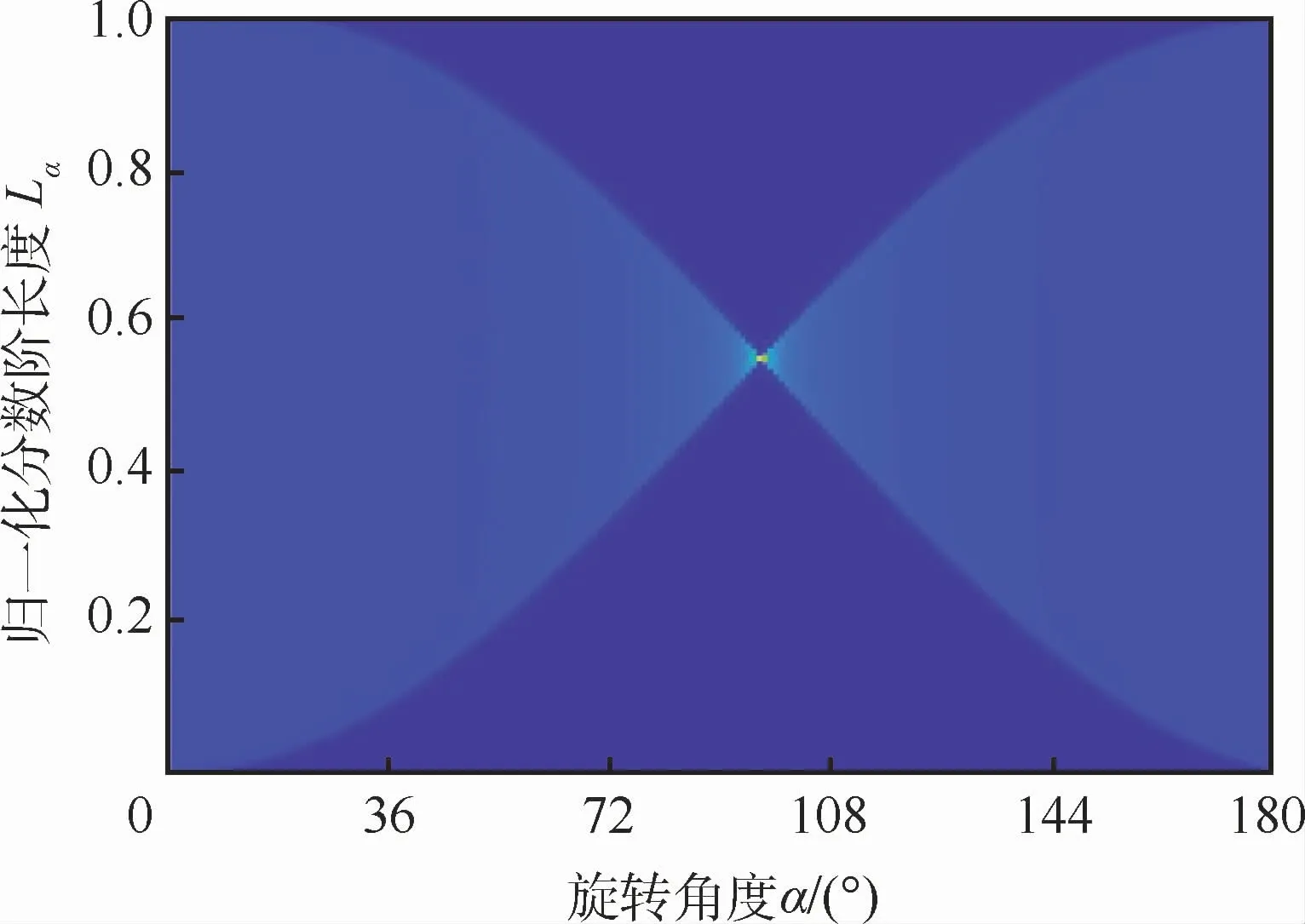
图1 LFM信号在不同旋转角度的分数阶长度Fig.1 Fractional order length of LFM signal at different rotation angles

令x1=α1-φ,x2=α2-φ,将等式右侧进行泰勒展开,得到
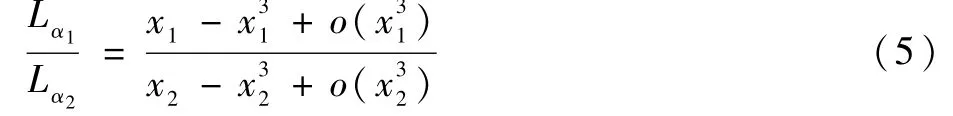
当x1,x2<1时,

即当旋转角度α接近最优旋转角度αo时,Lα和旋转角度距最优旋转角度的距离α-αo近似成正比关系,如图2所示。
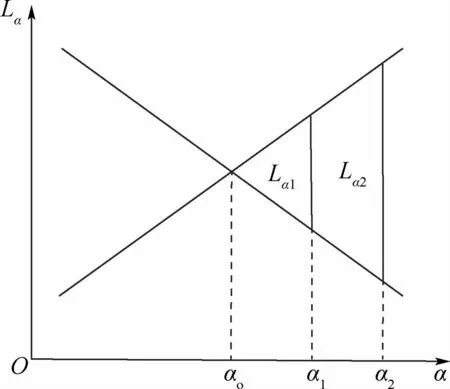
图2 旋转角度与分数阶长度关系的理想模型Fig.2 Ideal model of relationship between rotation angle and fractional order length

根据三角形相似原理,进行简单的几何推导,可得最优旋转角度的估计值为此时˜αo较接近理想旋转角度αo,为进一步提高估计精度,考虑以为搜索中心,搜寻获取最优旋转角度的精确值。具体描述为:寻找LFM信号在最优旋转角度形成的冲激信号,根据冲激信号参数及旋转角度,对信号时域参数进行估计,如下:
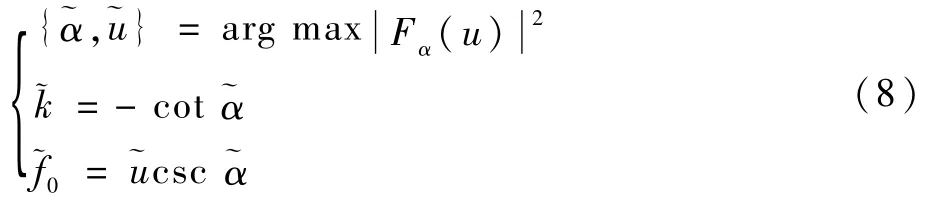
多分量LFM信号是各个单分量LFM信号的线性叠加,如下:

根据FRFT的线性特性,在分数域中多分量LFM信号频谱图中表现为出现平行于u轴的直线段的突变。图3为一个二分量LFM信号在FRFT变换中的函数图像。
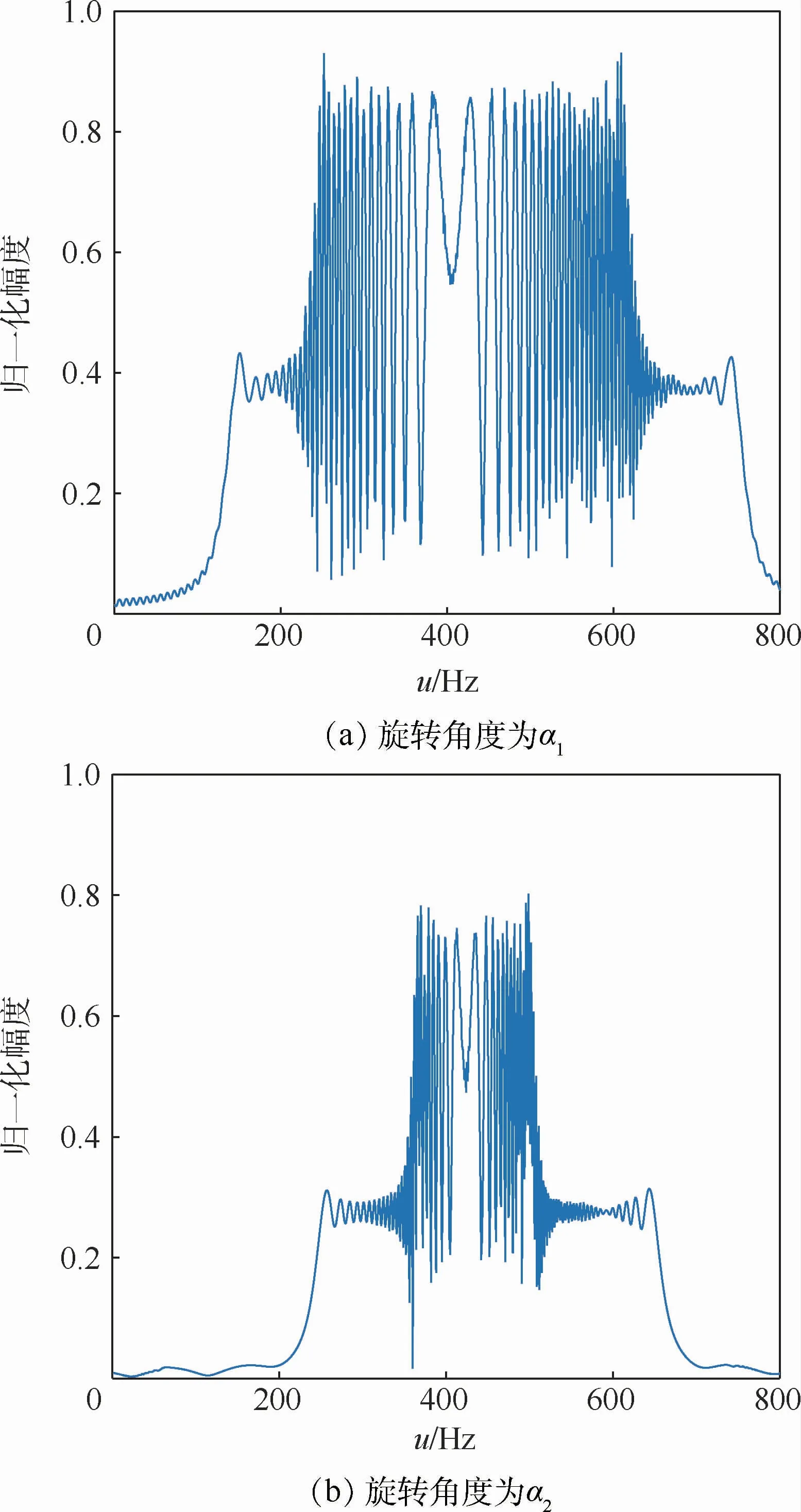
图3 两个LFM信号相加时的FRFT功率谱Fig.3 FRFT power spectrum of two added LFM signals
本文借鉴CLEAN 思想,首先研究某分量LFM信号,利用上述方法估计该分量的精确参数,并在相应的分数域中对该分量精确剔除;然后将剔除后的信号返回FRFT的初始旋转角度,继续对下一目标进行搜索、参数估计和剔除;设定最低门限,直到所有信号都被检测出来为止。
2 多分量LFM 信号检测原理
在运用上述原理进行多分量LFM 信号检测与参数估计时,需要先确定初始旋转角度α1和α2。根据文献[13],α取值范围为[π/4,3π/4]时,可得到信号的理想分数阶直线;又因为分数阶旋转角度α和分数阶次p的关系为α=pπ/2,所以p的取值范围为[0.5,1.5];结合仿真经验,本文取p1、p2分别为0.7和0.75。同时在进行信号的分数域分析时,由于时频域单位不统一,导致计算存在误差。参考文献[14],对信号进行单位归一化处理,取归一化尺度因子S=(t0/fs)1/2,t0为采样时间,fs为采样频率。
2.1 多分量LFM 信号检测算法
LFM信号功率谱分布存在规律,随旋转角度与最佳旋转角度的差值变化。根据文献[15],单分量LFM信号f在旋转角度α的分数阶幅度为
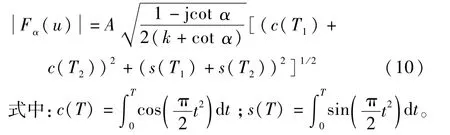
当信号的调频系数k为固定值时,其函数图像如图4所示。
根据功率谱函数表达式及其函数图像可得:
1)当旋转角度等于最优旋转角度时,其FRFT功率谱表现为冲激函数。
2)在靠近最优旋转角度时,分数阶幅度增长速率越来越快,几乎成指数增长;在远离最优旋转角度时,分数阶幅度缓慢减小,且幅值不大。
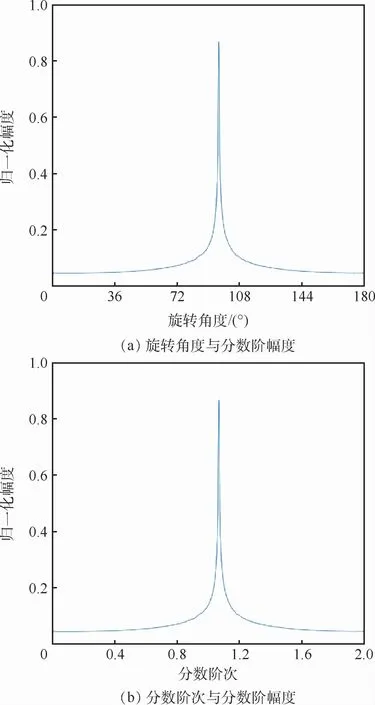
图4 旋转角度、分数阶次与分数阶幅度关系Fig.4 Relationship between rotation angle and fractional order amplitude,fractional order and fractional order amplitude
根据上述变化规律,本文采取以下搜寻算法:步骤1 根据式(7)计算最优分数阶次的初始搜索中心
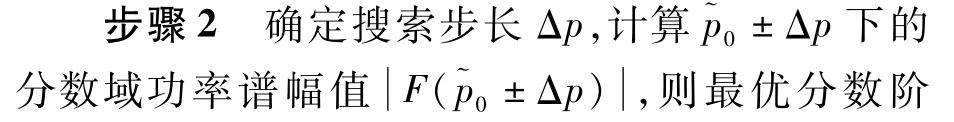


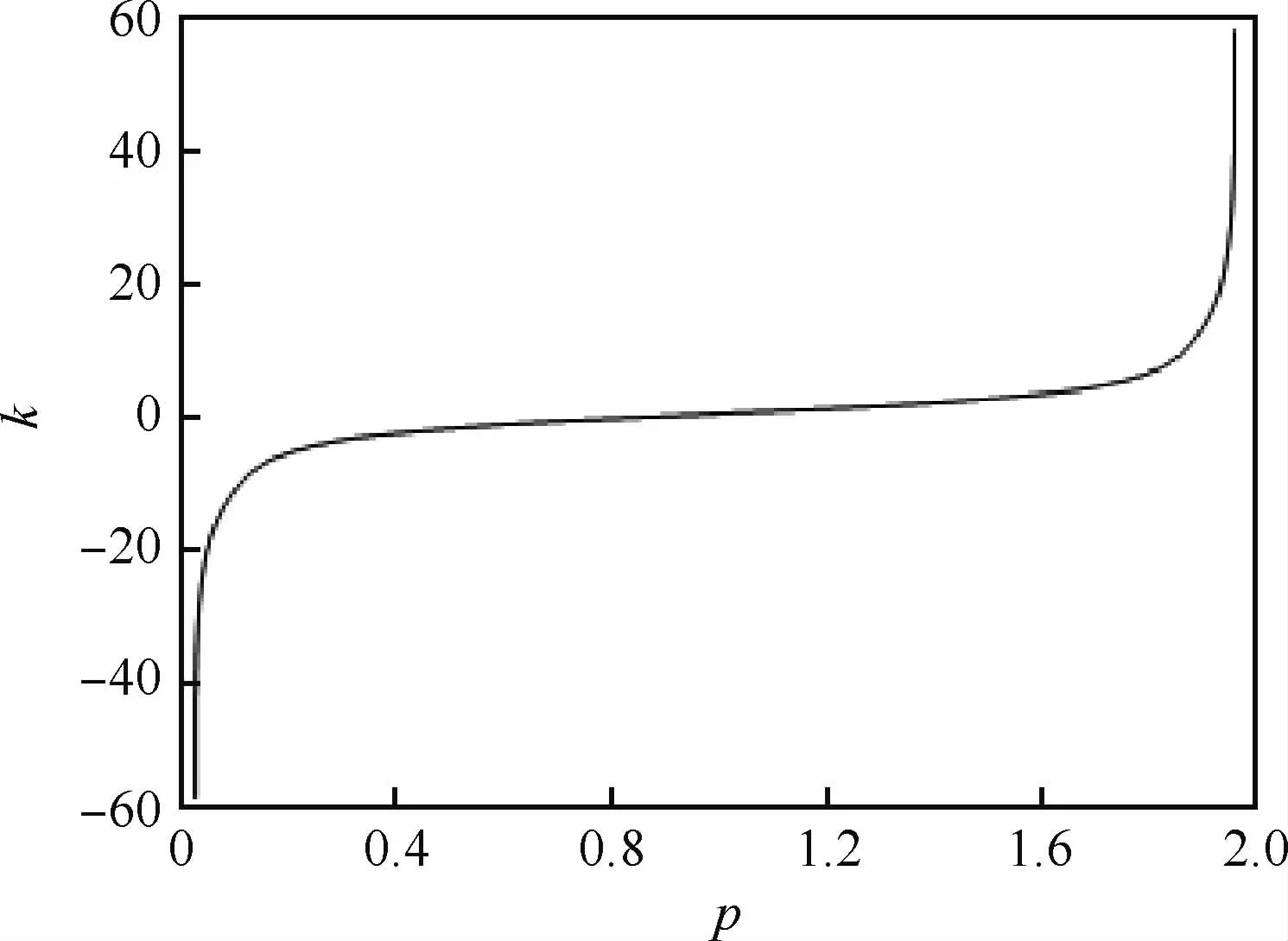
图5 chirp信号调频系数k与最优分数阶次p关系Fig.5 Relationship between frequency modulation coefficient k of chirp signal and optimal fractional order p


步骤6 根据式(8)估计该分量信号参数,并在相应分数域将该信号精确剔除,剔除后返回到步骤1进行下一分量的估计。
步骤7 设定门限值,重复步骤1~步骤6,直到精确估计出所有LFM分量。
2.2 计算量分析
在对多分量LFM 信号的各个分量进行参数估计时,主要运算集中在不同分数阶次FRFT的计算。当噪声影响及多分量LFM 信号间干扰较小时,对各信号分量的功率谱直线段长度估计就越准确,而搜索中心就越接近最优分数阶次。

结合式(7)、式(11)可得有噪声干扰状态与无噪声干扰状态下的初始分数阶次之间相差n次搜寻:
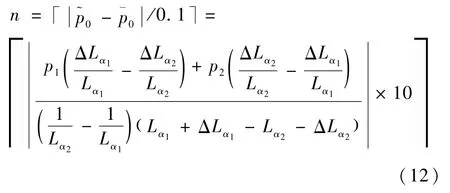


假设对信号取N点采样,则进行一次FRFT变换需O(N lg N)次运算,那么对单分量FM 信号参数的精确估计需O(15.5N lg N)次运算。相比于传统搜索算法,要达到最优分数阶次为0.000 1的估计精度,需要20 000次分数阶傅里叶变换,本文算法在保证估计精度的前提下运算量显著降低。
2.3 噪声影响
在低信噪比条件下使用上述搜寻算法时,本文采取多项式拟合的方法进行信号处理,分别在时频域对信号进行S-G滤波,以便确定LFM信号在初始分数阶次的分数阶长度。首先对时域采样信号平滑去噪,在尽量减小失真的情况下获取清洁信号;然后在分数域扩大移动窗长度求均值,获取频谱图像的直线段长度。
对信号采用S-G FIR平滑滤波器进行平滑滤波,其滤波原理如下:确定移动窗长度,在移动窗内利用最小二乘原理,对数据进行多项式拟合。假设对时域采样信号平滑降噪时,拟合多项式阶次为n1,移动窗长度为N1;对分数域信号求均值时,多项式拟合阶次为n2,移动窗长度为N2。为减少时域信号失真,在较短窗范围内,选取高阶多项式进行平滑去噪,这里取N1=N/80,n1=5;在分数域求平均时,应该划定较大的窗范围,这里取N2=N/8,n2=0。
图6为单分量LFM信号在采样点为800时,进行本文算法处理得到的变换图像。经过图形对比可以看出,用本文算法滤波后的图形更容易确定信号的分数阶长度。

图6 采样信号在旋转角度α1 时的分数阶幅度Fig.6 Fractional order amplitude of sampled signal at rotation angle α1
3 模拟仿真
1)仿真1
验证噪声对多分量LFM信号检测与参数估计产生的影响。根据2.2节分析,噪声功率过大时将无法提取LFM 信号的分数阶长度,而分量之间的相互干扰主要在小范围内影响所获取分数阶长度的准确度。本仿真研究本文方法的抗噪能力,即在有噪声情况下提取LFM信号分数阶长度的性能。考虑将问题简化,选用单分量LFM 信号替代多分量LFM信号进行测试。信号表达式如式(13),幅值为1,采样频率为600Hz,采样时间为2 s,采样点数为1201个。
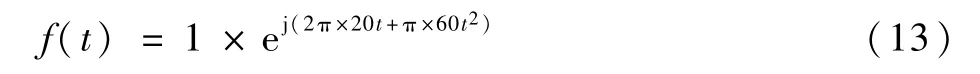
先在无噪声条件下进行多次参数估计,获取平均误差;再在此基础上,进行不同信噪比条件下的信号检测,获取检测概率。
仿真结果为:调频系数平均估计值为60.0935,绝对误差为0.093 5,相对误差为1.56×10-3;初始频率平均估计值为19.870 7,绝对误差为0.129 3,相对误差为6.47×10-3。给信号加入高斯白噪声,当信噪比为[-10,0]dB条件下,在不同信噪条件下分别模拟仿真100次,得到成功检测并精确估计出信号参数的概率,如图7所示。由此可知,当信噪比大于-6 dB时,成功检测信号的概率可达到90%以上;当信噪比降低到-7 dB时,成功检测信号的概率降低到50%;当信噪比降低到-9 dB时,随着噪声增大,信噪比降低,成功检测信号的概率稳定在5%左右。
2)仿真2
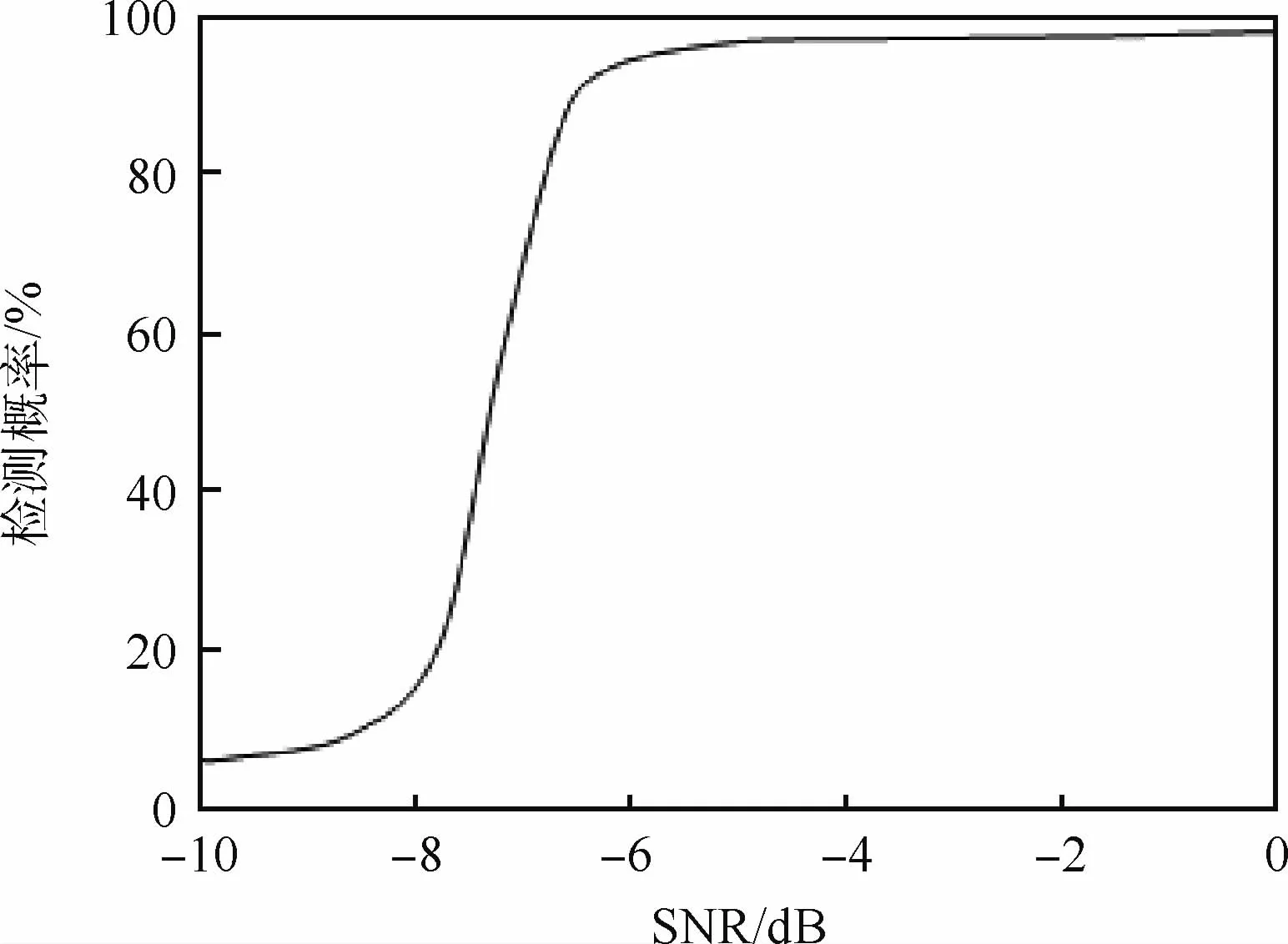
图7 不同信噪比条件下信号的成功检测概率Fig.7 Probability of successful signal detection under different SNRs
为验证本文方法对多分量LFM 信号检测与参数估计的有效性,设置三分量LFM信号的参数估计。信号表达式见式(14),采样频率为600 Hz,采样时间为2 s,采样点数为1 201个,为使仿真更具一般性,给信号加入高斯白噪声,使信噪比达到-3 dB,仿真结果如表1所示,表中pi表示第i分量对应的最佳分数阶次估计值。
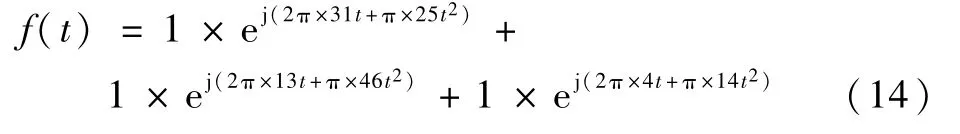
结果表明,在信噪比为-3 dB条件下,使用本文方法能快速准确地对信号各分量进行有效估计。但是在对每一分量进行参数估计时,由于在分数域未将相应的信号分量滤除干净,存在相同分量的重复检测现象。该现象不对方法精度造成影响,但进行多分量LFM 信号参数估计时,该现象增加了对每一分量的检测次数,降低了整体方法效率。
3)仿真3
本仿真验证本文方法的运算量。将仿真1中单分量LFM信号在不同信噪比条件下的仿真运算次数记录于表2;将仿真2中信噪比达到-3 dB条件下,三分量LFM 信号检测时,进行20次试验,将各个分量平均运算次数记录于表3。
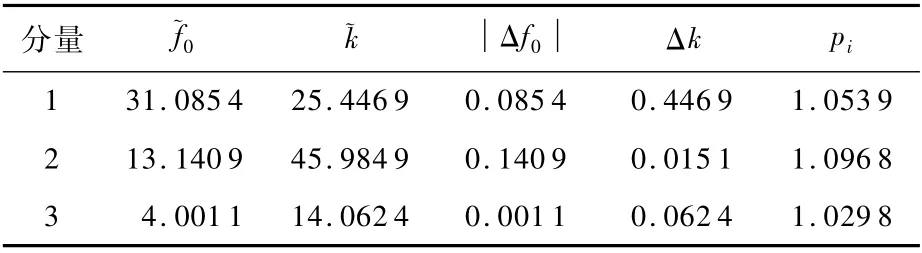
表1 三分量LFM 信号检测与参数估计仿真结果Table 1 Simulation results of three-component LFM signal detection and parameter estimation
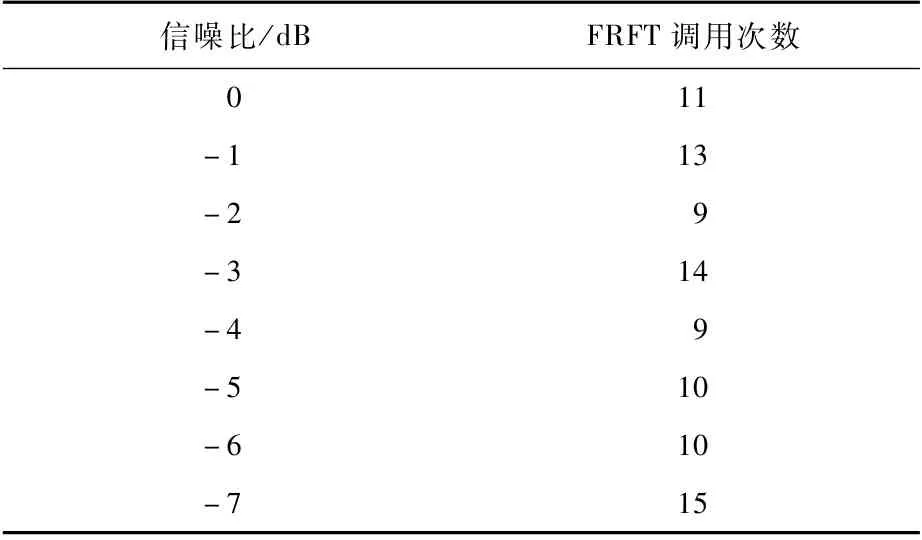
表2 单分量LFM 信号FRFT调用次数与信噪比Table 2 FRFT calls and SNR of single-component LFM signals

表3 三分量LFM 信号运算次数Table 3 Operation times of three-component LFM signals
分析表2数据,对单分量LFM 信号参数估计时,进行FRFT运算次数基本上与理论分析值相符,但少于理论分析中的15.5次运算,这是由所选的信号参数决定的,当选取大量不同参数的信号进行模拟仿真时,平均运算量将接近理论值;分析表3数据,对三分量LFM 信号参数估计时,平均对每一分量的FRFT运算次数都超出理论值的2~3倍,这也反映出由于在分数域未将已估计分量滤除干净,所导致的相同分量重复检测现象。
4 结 论
本文提出了一种多分量LFM 信号检测和参数估计的方法——利用FRFT的线性性质,对各分量单独分析,每次寻找一个分量的分数阶冲激函数,估计该分量的参数,然后在分数域将其剔除。
1)利用信号各角度FRFT之间的几何关系,提出最优分数阶次粗略值˜po的计算方法,且˜p o距离最优分数阶次po误差可达到0.1以内。
2)进一步提高估计精度,按照信号的分数阶幅度分布规律,提出一种高效的搜寻算法。
3)为克服各信号分量之间的相互干扰及噪声影响,分别在时域和频域进行阶数和窗长度不等的S-G滤波,提高精确估计出信号参数的概率。同时该方法在进行冲激函数剔除时存在不足,下一步可引入分数域滤波器,减少对同一分量的重复检测。

