对“√2是无理数的证明”的教学新探
张慧 常文武


摘要:无论从训练学生逻辑思维的角度,还是从数学史进课堂的角度看,“2是无理数的证明”都是非常好的选题。但是,教材提供的代数证法,学生很难接受和理解。对此,教学设计尝试采用几何证法,并以一个寓言故事为引子,同时融入折纸活动。
关键词:无理数;几何证法;折纸;教学设计
一、问题提出
初中生大概都会经历两个经典的数学证明,其中一个是勾股定理的证明,另一个是√2是无理数的证明。勾股定理(西方称之为毕达哥拉斯定理)无须赘言,是初中几何的基础。其证明学生必须掌握。而√2的无理性最早是毕达哥拉斯的弟子希帕索斯发现的,它是一个代数命题,引发了一次重大的数学危机。其证明是选学内容(现行各版本的初中数学教材均将其代数证法作为拓展阅读材料),教师通常略过不讲,而让学生自己阅读理解。
笔者认为,无论从训练学生逻辑思维的角度,还是从数学史进课堂的角度看,“√2是无理数的证明”都是非常好的选题。那么,对于教材提供的方法,学生的理解和掌握情况如何呢?下面是笔者与某位数学“资优生”的对话——
师 你了解√2是无理数吗?
生 了解。
师 知道怎么证明吗?
生 学过,让我想想。
(学生沉思。)
师 能不能写下来。
生 (写)设√2=q/p,则2=q2/p2,2p2=q2……
(学生出现卡顿。)
师 q/p是什么样的分数?
生 约过分的最简分数。
师 那么,p和q怎么样?
(学生迟疑。)
师 没有公因数哦。接下来怎么办?
(学生迟疑。)
师 可见右边是偶数。
生 对对对,q是偶数。再设q=2k……后面忘了。
师 你尝试把q=2k代入上式看看。
生 哦,可得p2=2k2,然后呢?
師 由此发现p的奇偶性是什么?
……
可见,对于教材提供的方法,学生刻意模仿都很困难。其实,对初中生而言,证明本来就比较陌生,反证法则更加陌生。如果刻板地教或让学生看教材上的证明,只会让学生畏惧证明。所以,我们尝试给出一种新的证明方法及教学设计,帮助学生理解这个命题及其证明。
二、教学设计
我们尝试采用几何方法来证明这个命题,并以一个寓言故事为引子。教学主要包含如下几个步骤:
(一)故事导引
根据“龟兔赛跑”的故事,创设“龟兔同行”的问题情境:
一只乌龟和一只兔子,它们是好朋友。乌龟和兔子,一个爬着行,一个立着跳。如图1,乌龟爬一个身子的距离(每个身段之间无足迹)是某等腰直角三角形的斜边,兔子跳一下的跨度是该等腰直角三角形的直角边。请问:如果它们一开始齐头并进地去散步,并一直这样走下去,它们的足迹会在某处再次重叠吗?
这个问题情境化沿用了龟兔赛跑的寓言,便于学生形象直观地理解问题。而且,暗合了当初希帕索斯发现√2的问题原型:兔子跳一下的跨度就是正方形的边长,乌龟的身长就是相应正方形的对角线长。
(二)结论数学化
通过该问题的解决,得出结论:无论用多么精细的尺子的一格当1,量出的等腰直角△ABC的斜边AB与直角边BC的长度不可能都是整数。
(三)结论证明
运用反证法,具体如下:
如图2,作等腰直角△ABC斜边AB上的高CD,并且继续作由高分割得到的一个小等腰直角三角形斜边上的高DE、EF……我们可以得到一系列旋转变小的等腰直角三角形。显然,这个过程可以无限地进行下去。
现在假设在规定了非常细小的单位长度(例如原子的直径)后,用这把非常精细的尺子度量AB与BC,发现它们都是整数。我们开始推演:
由勾股定理,AC2+BC2=AB2,即2BC2=AB2。
由BC是整数知2BC2是偶数,得AB2也是偶数,得AB是偶数(奇数的平方为奇数,偶数的平方为偶数),从而AB的一半,即高CD也为整数。
在等腰直角△BCD中,斜边BC和直角边CD同为整数,同理,又能推得高DE为整数。
如此这般,一连串的高EF、FG、GH、HI……都将是整数。
这些高显然是一串无限、不断递减的数。它们永远保持是整数,可能吗?
这是不可能的,因为无论一开始的斜边AB长多么大,其对应的高CD已经减半,而CD上的高EF又将减半……再大的数不停地对半折损,最终一定会小于1。
所以,问题就出在一开始的假设不合理。于是,我们就得承认任何等腰直角三角形的斜边、直角边的长度都不能同时为整数。
(四)问题解决
设兔子跳一下的跨度,即某等腰直角三角形直角边的长度为1,则乌龟的身长,即该等腰直角三角形斜边的长度为√2。
假如乌龟和兔子的足迹在某处再次重叠,就意味着乌龟身长的m倍等于兔子跳了n下的跨度,即m√2=n,两边平方得2m2=n2,根据勾股定理的逆定理可知,以整数m当直角边长,整数n当斜边长,可构成一个等腰直角三角形。
这就与前面我们证明过的结论矛盾了。所以,乌龟和兔子无论走多远,足迹都不会在某处再次重叠。
三、学具使用
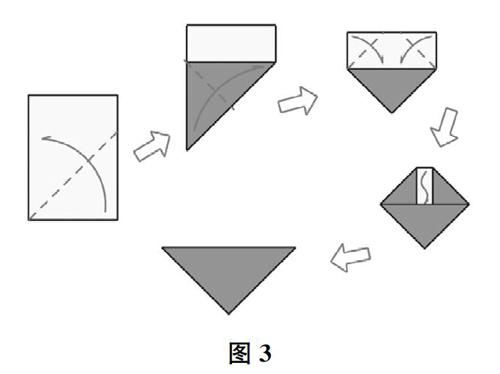
在上述证明中,得到图2,除了直接画图之外,还可以使用学具:2n(n为整数且大于等于2)个同样大小的等腰直角三角形拼成大的等腰直角三角形。而每一个等腰直角三角形都可以通过折纸得到,具体方法如图3所示。
四、教学反思
几何方法让学生对抽象的“2是无理数”有了直观、清晰的理解,寓言故事拉近了数学与生活的距离,折纸活动使得数学更平易近人。
数学证明教学的本意是培养学生的逻辑推理能力,但是过分注重形式的严密往往让证明变得枯燥和晦涩。牺牲一些表达的简洁但不失去逻辑的严密,往往能让数学证明变得易于接受,也不违背数学证明教学的初衷。
实践表明,数学史与数学文化内容以及动手做活动在精心的安排下可以进入寻常的课堂,成为润物无声的教学素材和新颖的教学手段。

