基于柔性销结构的风电齿轮箱有限元仿真分析

郑传统，周杜

基于柔性销结构的风电齿轮箱有限元仿真分析

郑传统，周杜

（明阳智慧能源集团股份公司 风能研究院，广东 中山 528437）

以某型号柔性销轴结构的风电齿轮箱行星传动系统为研究对象，分析了柔性销轴的基本结构和均载原理；利用有限元方法对风电齿轮箱进行静强度计算、变形分析和齿轮接触应力分析；结果表明：柔性销结构的等效应力、齿轮齿根的弯曲应力、齿面上的接触应力均满足要求；套筒母线上的位移曲线近似一条直线，说明销套在受载情况下保持平行移动；齿轮接触应力在沿齿宽方向分布基本一致。柔性销结构能实现风电齿轮箱齿轮间均载性。

风电齿轮箱；柔性销；均载特性；有限元

风电齿轮箱作为风力发电机组最重要的核心部件之一，诸多专家学者对其齿轮的强度做了深入系统的研究[1-4]，至今，对齿轮强度有三种研究方法：数值解析法、有限元仿真分析法和实验法。国内外的风电齿轮箱制造厂同样投入了大量的资金和研发力量对其进行开发研制。双馈齿轮箱的行星架采用双壁式支撑结构，这种结构在受载时，会引起齿轮间的载荷分布不均匀。轴承也是风电齿轮箱传动系统中的核心部件之一，其工作性能直接影响到齿轮的传动精度、噪声、振动，增加齿轮传动早期失效的可能性。因此，掌握滚动轴承正确的有限元仿真分析方法[5]，不仅可以在齿轮箱柔性销结构设计阶段对其设计的合理性进行准确的仿真分析，还能在齿轮箱系统分析时，准确模拟设计齿轮的修形量，从而有效减少轮齿因各零部件的受载变形和制造误差引起的啮合冲击，获得较理想的均布载荷，提高齿轮的啮合性能和承载能力。采用柔性销轴技术[6-9]，既可以减轻行星架的重量，使齿轮箱内部更紧凑，还能显著降低行星轮间的均载系数。柔性销轴风电齿轮箱的增速比大、传递功率高，且承受复杂的工况，尤其是低速级的行星轮，承受着很大的负载。风电齿轮箱一般要求满足20年的寿命，而柔性销轴风电齿轮箱具有高紧凑性、高可靠性的特点。因此对其进行强度校核及均载性能分析具有重大的工程意义。

1 柔性销轴基本结构和均载原理

如图1所示，行星轮通过套筒和柔性销固定在行星架上，由于柔性销和套筒为双悬臂结构，当内齿圈与太阳轮的两个切向啮合力F、F施加于行星轮上时，行星销轴的支撑力为F，F＝2F。套筒受力可近似为在其轴线方向的均布载荷，＝F/。为行星轮轴承内圈与套筒的配合长度。行星架对悬臂销轴在点处的支撑力F、弯矩M，所引起的角度、挠度被相反方向来自另一端点悬臂套筒的对销轴的剪力F、弯矩M引起的角度、挠度所抵消。点为的中点，y为处的挠度，这种结构保证了齿向的均载性。

图1 行星轮与行星轴受力情况

当柔性销轴中心承载时，其作用效果如图1所示，柔性销轴偏转成S型，可以确保行星轴在变形过程中是水平的，并且轴承对柔性销轴的力垂直于轴线。

2 柔性销轴校核方法

利用材料力学[10]校核柔性销轴弯曲强度。

由弯曲强度准则可知：

式中：K为制造和安装误差对销轴载荷影响系数，取1.35～1.5；max为销轴上的最大弯矩，N·mm；为抗弯截面系数；max为销轴上的最大正应力，MPa；[]为销轴的许用正应力，MPa。

将几何尺寸代入式（1），可得：

式中：为作用在轴套上的载荷，N；为销轴直径，mm。

销轴安全系数为：

柔性销轴的最大挠度为：

式中：为抗弯刚度，N/mm2；为销轴的弹性模量，MPa；为销轴的截面惯性矩，mm4。

以上计算分析方法是假定销套受到的力是沿轴线均匀分布的线载荷，但实际上载荷并非沿其轴线均匀分布的，同时，此计算方法无法考虑轴承游隙对载荷分布的影响，因此必须采用有限元方法对柔性销轴进行仿真分析。

3 圆柱滚子轴承有限元仿真分析方法

轴承是风电齿轮箱传动系统中的核心部件之一，其高度的非线性特性很大程度上影响着其相邻部件的承载能力，在风电齿轮箱系统仿真分析时，能否对轴承进行正确建模是风电齿轮箱系统仿真分析的关键，必须准确模拟轴承的受载情况。然而滚动轴承是由滚子和内外圈组成的高度非线性结构，全部实体建模将会带来复杂的非线性运动和接触关系，仿真分析很难收敛。

在轴承行业应用中，用抗压不抗拉的非线性弹簧模拟滚动体与内外圈滚道的接触关系已被认可，这种分析方法不仅工作量较少，而且能够精确模拟轴承在实际工况下滚动体与内外圈滚动的接触与力传递情况。

滚子采用弹簧单元，弹簧采用非线性弹簧，不考虑受拉刚度，仅考虑受压刚度，弹簧刚度值由《机械设计手册》[11]中的Hertz计算公式得到。

如图2所示，ISO 16281[12]中给出了按赫兹接触理论推导出的滚子与内外圈滚道接触总变形的理论公式为：

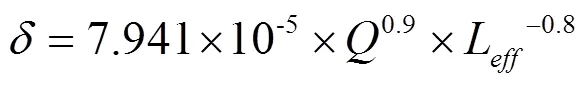
式中：为单个滚子与内外圈滚道的接触力，N； L为滚子有效长度，mm；为滚子与内外圈滚道接触总变形，mm。

用有限元按式（5）建立非线性弹簧对滚动轴承进行仿真计算的过程中，值必须大于滚动轴承在实际运行过程中单个滚子所承受的最大载荷，否则可能无法收敛，约取滚子最大载荷的1.5倍。滚动轴承在实际运行过程中，单个滚子所受的最大载荷为：

则：

式中：F为轴承所受径向力，N；为滚子数量。

图2 圆柱滚子轴承受力情况

非线性弹簧模拟圆柱滚动轴承的有限元建模方法为：

（1）将内外圈滚道按滚子数量划分成份，每一份代表滚子与内外圈的作用位置。

（2）在内外圈滚道上，按滚子与内外圈滚道接触的实际有效长度（滚子总长减去两端倒角），将滚道沿轴向均分为份（一般取5～8）。

（3）按步骤（1）、（2）在内外圈滚道划分每列滚子作用的位置上、在对应的划分节点上分别建立线性弹簧，如图3所示。

（4）按式（7）计算出，则每根弹簧所受的载荷为：

（5）每根弹簧在滚道上有效作用长度为：

（6）将式（8）、式（9）代入式（5），则每根弹簧的刚度曲线计算公式为：

（7）要真实模拟滚动轴承滚子与滚道的接触，建立的非线性弹簧只能承受压力不能承受拉力，在有限元分析过程中，弹簧受压时力和位移都是负值。因此，在用Excel编写弹簧的刚度曲线值时，需将力和位移都转换为负值。

（8）修改有限元生成的inp文件，将所有的线性弹簧修改为非线性弹簧。

（9）将更改为非线性弹簧的inp文件提交有限元软件进行计算分析，如图3所示。

4 柔性销轴风电齿轮箱有限元分析

如图4（a）（b）所示，根据某型号风电齿轮箱一级行星传动系统三维模型，考虑行星架、销轴、销套、行星轮、太阳轮、内齿圈、行星轮轴承，其中行星轮轴承滚子用非线性弹簧[5]代替，对该模型进行有限元分析。柔性销轴齿轮箱系统仿真建模过程如下：

（1）由于整个行星级模型结构和载荷的周期对称性，为了提高计算效率，有限元仿真分析模型只建1/，为行星轮数目，如图4（c）所示；

（2）模型两侧面建立周期对称约束；

（3）按实际情况采用过盈接触；

（4）齿圈螺栓孔面、太阳轮花键部位均固定约束；

（5）齿轮啮合面均建立正常接触关系，接触部位网格细化处理，如图5所示；

（6）扭矩载荷施加在行星架孔的中点。

图3 轴承有限元模型

图4 一级行星系统

图5 啮合齿轮局部网格细化

各零部件的材料属性如表1所示。

表1 零件材料属性

根据ISO 6336[13]可知，齿轮的许用接触应力σlim＝1500 MPa，许用弯曲应力σlim＝500 MPa。

从图6可以看出，销轴的最大Mises应力为726 MPa，销套的最大Mises应力为487 MPa，均小于材料的屈服强度。

提取图7套筒母线上的位移值，得到图8，可以看出，在受载条件下，套筒基本能保持平行移动。

图6 销轴、销套Mises应力

图8 套筒母线上的位移曲线图

从图9可以看出，齿轮接触线上的接触应力呈现出两侧应力值偏大、中间应力值较为均匀的特点，这是没有考虑齿轮修型造成的。内齿圈上最大接触应力为637 MPa，行星轮与内齿圈啮合处的最大接触应力为659 MPa，这是两者的网格密度不一致造成的，且在数值上相差不大，符合计算要求。太阳轮上最大接触应力为1165 MPa，行星轮与太阳轮啮合处的最大接触应力为1222 MPa。均小于齿轮的许用接触应力σlim＝1500 MPa，齿轮接触强度满足要求。

分别提取内齿圈、太阳轮上接触线上的应力值，得到图10，可以看出，啮合齿轮在实际工作中倾斜量很小，啮合面近似平行。

从图11可以看出，内齿圈、太阳轮、行星轮的最大齿根弯曲应力依次为169 MPa、148 MPa、248 MPa，均小于许用弯曲应力σlim＝500 MPa，齿轮弯曲强度满足要求。

5 结论

本文在柔性销系统分析中采用非线性弹簧模拟轴承建模，并在考虑轴承游隙的情况下精确模拟轴承对系统载荷分布的影响；采用柔性销结构的风电齿轮箱能实现齿间载荷的均匀性；在柔性销传动系统分析中，准确模拟齿轮啮合非线性接触对柔性销强度和变形的影响，为后期进行齿轮箱瞬态动力学仿真打下了技术基础；掌握了齿轮和轴承非线性有限元仿真分析的正确方法，为传动链系统、偏航系统、变桨系统的开发及仿真分析奠定了基础。

图9 接触应力云图

图10 齿轮上的接触应力曲线图

图11 齿根弯曲应力云图

[1]徐向阳，朱才朝，刘怀举，等. 柔性销轴式风电齿轮箱行星传动均载研究[J]. 机械工程学报，2014，50（11）：43-49.

[2]邱育潮. 柔性销轴式风电齿轮箱行星传动均载研究[D]. 重庆：重庆大学，2015.

[3]李飞. 行星齿轮传动柔性销轴比例模型的微动疲劳特性研究[D]. 湘潭：湘潭大学，2016.

[4]苏中华. 风电齿轮箱柔性销轴结构的优化分析[D]. 西安：西安工业大学，2017.

[5]王金明，邓小梅. 非线性弹簧单元的圆柱滚子轴承非线性刚度和应力分析[J]. 江西化工，2017（2）：75-78.

[6]方振江，华青松，马文勇，等. 风电增速齿轮箱功率分流和柔性销的设计计算[J]. 机械传动，2016（12）：85-88.

[7]尚振国，陈凤艳，蔡卫国，等. 海上风电齿轮箱柔性销结构有限元优化设计[J]. 机械设计与制造工程，2015（7）：16-18.

[8]孟高强. 基于柔性销技术平台的风电齿轮箱设计探析[J]. 机械，2017（3）：55-58.

[9]贺伟. 行星传动柔性销均载特性分析[J]. 现代机械，2018（3）：42-44

[10]刘鸿文. 材料力学[M]. 5版. 北京：高等教育出版社，2011.

[11]汝元功，唐照民. 机械设计手册[M]. 北京：高等教育出版社，1995.

[12]ISO/TS 16281: 2008，Rolling bearings Methods for calculating the modified reference rating lifefor universally loaded bearings[S]. International Organization for Standardization，Geneva，Switzerland，2008.

[13]ISO Standard 6336: 2006，Calculation of load capacity of spur and helical gears (Part 5) [S]. International Organization for Standardization，Geneva，Switzerland，2006.

Finite Element Simulation Analysis of Wind Power Gearbox Based on Flexible Pin Structure

ZHENG Chuantong，ZHOU Du

( Wind Energy Research Institute, MingYang Smart Energy Group Limited, Zhongshan 528437, China )

In order to study the planetary transmission system of a certain type of flexible pin shaft structure, the basic structure and load sharing principle of the flexible pin shaft are analyzed briefly. The static strength calculation, deformation analysis and gear contact stress analysis are carried out by using the finite element method. The results show that the equivalent stress of the flexible pin structure, the bending stress of the gear root and the contact stress on the tooth surface meet the requirements of performance. The displacement curve on the sleeve bus is approximately a straight line, which means that the pin sleeve keeps parallel movement under loaded conditions. The contact stress distribution of the gear is basically the same along the tooth width direction. The flexible pin structure can realize load sharing between the gears of the wind power gearbox.

wind power gearbox；flexible pin；load sharing characteristics；finite element

TH131.6

A

10.3969/j.issn.1006-0316.2020.07.011

1006－0316 (2020) 07－0069－07

2019－10－29

郑传统（1981－），四川成都人，硕士研究生，工程师，主要从事风电齿轮箱仿真工作，E-mail：zhengchuantong@mywind.com.cn；

周杜（1993－），湖南湘潭人，硕士研究生，工程师，主要从事风电齿轮箱仿真工作。