异构多智能体系统分组输出时变编队跟踪控制
田磊,赵启伦,董希旺,4,*,李清东,任章,4
1. 北京航空航天大学 自动化科学与电气工程学院,北京 100083 2. 北京航空航天大学 飞行器控制一体化技术国防科技重点实验室,北京 100083 3. 北京电子工程总体研究所,北京 100854 4. 北京航空航天大学 大数据科学与脑机智能高精尖创新中心,北京 100083
随着科学技术的快速发展,世界各军事大国高度重视无人作战系统精确协同配合能力。由无人机、无人车组成的空地异构无人作战系统, 由于兼具无人机响应速度快、侦查范围广、通信能力强的特点以及无人车负载能力强、对地目标侦查精度高的优点,越来越受到各军事强国的青睐。
协同控制技术是空地异构无人作战系统实现优势互补与战斗力有机融合的基础,得到了广泛的重视和研究,近年来涌现出了丰富的研究成果。而编队控制作为协同控制的基础性研究之一,也取得了长足的发展。相比于单一个体,集群系统通过个体间的相互协作,能够以更小的代价完成难度、复杂度较高的任务,实现“1+1>2”的效果。例如,多个功能单一的卫星可以通过协同构成一个虚拟卫星,来完成更加复杂的深空探测任务[1],多架无人机保持编队队形可以有效减小空气阻力,降低燃料消耗[2]。另外,编队控制在协同围捕,协同打击,协同侦查方面也有重要的应用[3]。相比于集中式的控制策略,分布式控制策略的可扩展性和灵活性更高,计算效率更快[4]。一致性理论的发展为分布式编队的控制方法提供了理论支撑[5]。文献[6-8]给出了不同情况下基于局部邻居通信的编队控制协议。
在协同侦查、协同打击等任务中,无人作战系统在形成既定编队的基础上,还需要能够识别复杂多变的战场环境,快速穿越栅栏、防御工事等障碍物。因此,如何控制整个编队移动也是十分值得关注的问题,即编队跟踪问题。文献[9-11]分别采用滑模控制、鲁棒控制、自适应控制等方法,研究了单一智能体小组在不同条件下的时变编队跟踪问题,具有较好的实践应用价值。需要指出的是,单一编队能够解决的问题相对有限,大多数情况下,需要将系统中的智能体分为多个小组,通过小组间的相互协作,完成不同的任务。例如,在无人机协同攻击任务中,为提高突防能力与毁伤效能,需要先摧毁敌方的预警雷达、防空导弹发射阵地等防御系统,再摧毁指挥中枢等关键目标。相同小组内的无人机执行同一个任务,而不同小组之间的无人机则借助组间无线通信技术,在智能任务目标分配与自主决策规划的基础上,可采取不同的战术队形对各自的目标发动进攻。文献[12-13]给出了能够解决分组编队控制问题的控制协议,但各个小组独立性强,组间协同不明显。分组编队控制与编队跟踪控制结合所产生的分组编队跟踪问题目前仍是开放性问题,相关研究成果尚不多见。无人机协同探测、巡航、侦查等任务[14]都可以看作分组编队跟踪控制问题。
此外,已有研究成果大多以同构智能体模型为前提,即每个智能体的动力学模型是相同的,考虑到无人机与无人车的动力学模型存在较大差异性,文献[6-13]中的方法较难直接实现空地无人系统的协作配合,因此需要针对异构多智能体系统模型进行研究。文献[15-17]研究了异构多智能体系统的编队跟踪控制问题,但是文献中的领导者不存在控制输入,即整个系统的运动轨迹不能得到有效控制。文献[18-20]研究了领导者存在控制输入情况下的一致性问题,但系统模型不是异构的或系统的通信拓扑关系为无向连接,工程应用性受到一定限制。
为应对异构无人系统在有向通信下协作与配合带来的挑战,本文研究了高阶异构多智能体系统在有向拓扑条件下的分组输出时变编队跟踪控制问题。本文的主要贡献有:①采用全新的分组模型架构,组间和组内的协同作用明显,并且采用有向通信拓扑结构,减小通信带宽需求。②系统中的智能体均采用异构体模型,设计的控制协议能够解决异构高阶线性系统的分组输出时变编队跟踪控制问题,同时给出了该控制协议有效性的相关证明。
1 预备知识和问题描述
1.1 图论知识
拉普拉斯矩阵可以用来表征通信网络中各节点的连接关系。一个有q个节点的有向图G可以表示为G=(∂,),其中∂={ι1,ι2,…,ιq}表示节点的集合,⊆{(ιi,ιj):ιi,ιj∈∂}表示边的集合。用Ni来表示节点ιi邻居的集合。图G的邻接矩阵可以表示为W=[wij]∈Rq×q,当ιj∈Ni时,wij=1,否则wij=0。定义图G的度矩阵为进而拉普拉斯矩阵为L=D-W。如果图G中某一个节点到其他所有节点都存在有向连接,则称为图G中包含一个以该节点为根的生成树。
1.2 问题描述
本文中的系统模型设计为3层架构,包含1个 虚拟领导者、M个分组领导者和N个跟随者。所有智能体的模型可统一写为
(1)
式中:i=1,2,…,1+M+N;xi(t)∈Rni、ui(t)∈Rmi和yi(t)∈Rp分别为所对应智能体的状态、控制输入和输出;Ai∈Rni×ni为系统矩阵;Bi∈Rni×mi为输入矩阵;Ci∈Rp×ni为输出矩阵。


注释1在实际物理系统中,单个智能体的控制输入一定是有界的,不会是无限值,因此假设1 是合理的。
假设2输入矩阵Bi为列满秩矩阵,即满足rank(Bi)=mi,并且(Ai,Bi)可镇定,(Ci,Ai)可检测,其中i=1,2,…,1+M+N。
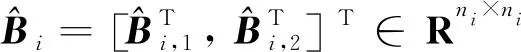
假设3有向图G中包含一个以虚拟领导者为根节点生成树,同时N个跟随者被分成M个小组,每个小组有且只有一个分组领导者,虚拟领导者和分组领导者之间是单向通信,虚拟领导者与跟随者之间不存在直接通信,分组领导者与其他分组领导者和其所在小组的跟随者通信,跟随者只与其所在小组的分组领导者和跟随者通信。
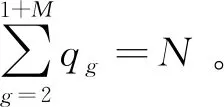
(2)
式中:LG,1、Lgro,1表征虚拟领导者与所有分组领导者之间的拓扑关系,相应的LG,g、Lgro,g表征分组领导者g与其所在小组的所有跟随者之间的拓扑关系。
注释2系统的拉普拉斯矩阵只有在假设跟随者为顺序标号时才能写成式(2)中的形式。需要指出的是,即便跟随者是乱序标号,但只要假设2 成立,通过简单的行列变换即可得到形如式(2) 矩阵形式。为方便后续表达,系统的拉普拉斯矩阵均采用式(2)的形式。
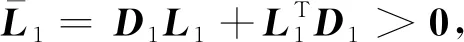
假设4对于分组领导者g=2,3,…,1+M,调节器方程:
(3)
存在矩阵对解(Eg,Fg);对于跟随者j=2+M,3+M,…,1+M+N,调节器方程:
(4)
存在矩阵对解(Ej,Fj)。
假设5对于分组领导者g=2,3,…,1+M,线性矩阵方程:
BgHg-EgB1=0
(5)
存在解Hg; 对于跟随者j=2+M,…,1+M+N,线性矩阵方程:
(6)
存在解Hj。
定义1对于任意给定的有界初始状态,如果式(7)关系成立,则称多智能体系统实现了分组输出时变编队跟踪控制。
(7)
式中:hg(t)、hj(t)分别为分组领导者层和跟随者层期望实现的输出时变编队。
2 控制协议的设计和系统稳定性分析
本节将给出控制协议的设计方法,对分组领导者和跟随者分开进行设计。
1) 对于分组领导者g=2,3,…,1+M,设计如下控制协议:
(8a)
(8b)
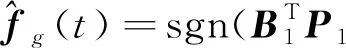
(8c)
(8d)
βgHgfg(t)+vg(t)
(8e)
(8f)
(8g)
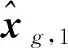
2) 对于跟随者j=2+M,…,1+M+N,控制协议设计为
(9a)
(9b)
(9c)
(9d)
(9e)
(9f)
βjHjfj(t)+vj(t)
(9g)
(9h)
(9i)
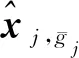
算法1对于智能体i∈{2,3,…,1+M+N},控制协议(8)、(9)采用以下步骤确定部分参数值。
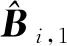
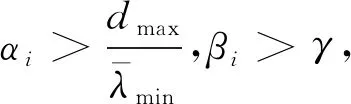
步骤3设计Ei、Fi和Hi使得矩阵方程(3)~(6)成立。
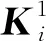
步骤5求下列Lyapunov方程的正定实对称解阵Qi∈Rni×ni:
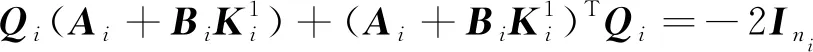
(10)
式中:Ini为ni×ni维单位阵。
算法2对于分组领导者g=2,3,…,1+M,求下列黎卡提方程的正定实对称解阵P1∈Rn1×n1:
(11)
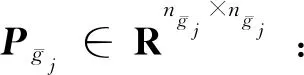
(12)
定理1如果假设4和假设5成立,分组领导者采用控制协议(8),跟随者采用控制协议(9),且以下时变编队可行性条件可以满足:
(13)
式中:i=2,3,…,1+M+N,则异构多智能体系统能够实现在有向拓扑条件下的分组时变编队跟踪控制。
证明:证明分为2个部分,首先证明观测器(8a)和(9a)的收敛性,进而证明在控制器(8e)和(9g)的作用下,异构多智能体系统能够实现在有向拓扑条件下的分组时变编队跟踪控制。对分组领导者和跟随者分开进行讨论:
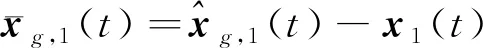
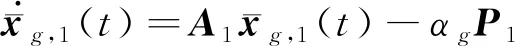
(14)
令
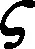
其中:1M表示元素全为1的M维列向量,进而可将式(14)改写为
(15)
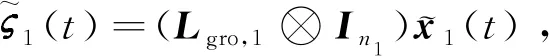
(16)
构造Lyapunov函数:

(17)
对Va,1(t)求导可得
(18)
由于βg>γ且以下关系式成立:
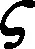
(19)
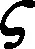
(20)
式中:g,k∈{2,3,…,1+M},进而推出

(21)
同理可以推出
(22)
由式(19)、 式(21)以及式(22)可得
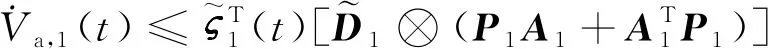
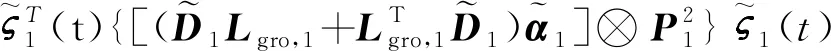
(23)
根据引理2、算法1的步骤2和算法2可知
(24)
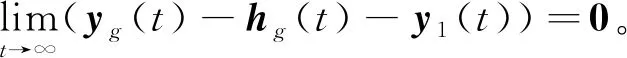
(25)
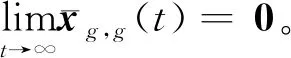
(26)

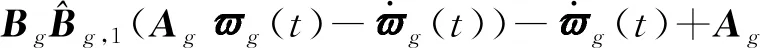
(27)

(28)
如果假设4和假设5成立,根据式(3)、式(5)和算法1中的步骤4,可将式(28)进一步化简为
(29)
考虑如下Lyapunov函数:
(30)
式中:g=2,3,…,1+M。对Vg,1(t)求导可得
(31)
式中:
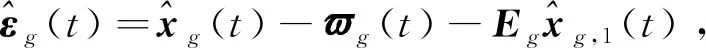
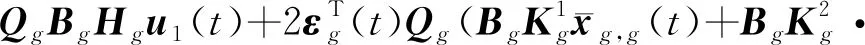
(32)
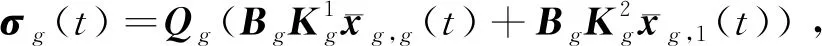
(33)
将式(32)、式(33)代入式(31)中并根据式(10)和式(30)可得
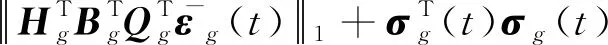
(34)
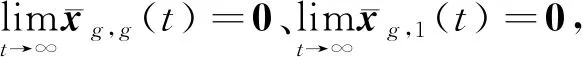
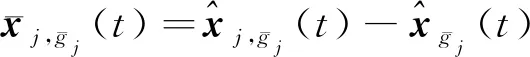
(35)
令
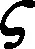
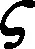
式(35)可改写为
(36)
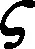
(37)
构造Lyapunov函数:
(38)
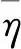
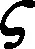
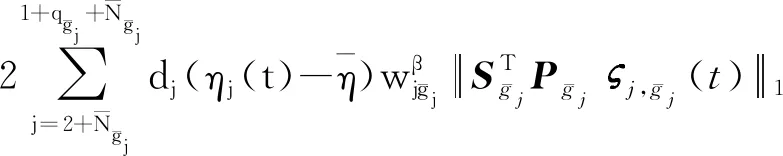
(39)
由于βj>γ且以下关系式成立:
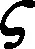
(40a)
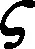
(40b)
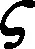
(41a)
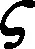
(41b)
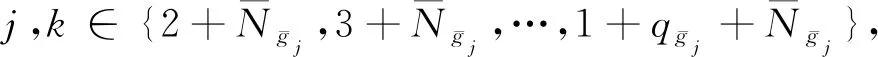
(42a)
(42b)
(43a)
(43b)
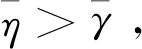
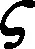
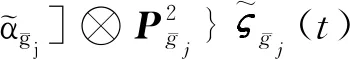
(44)
根据引理2、算法1和算法3可知
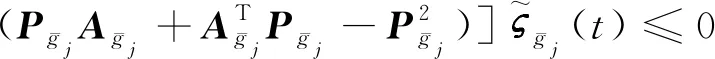
(45)
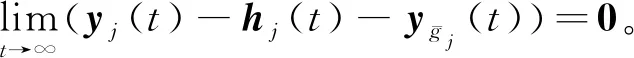
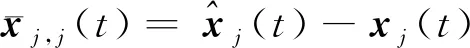
(46)
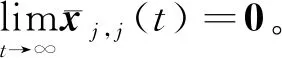
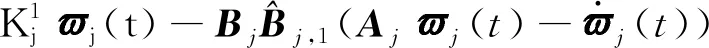
(47)
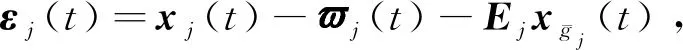
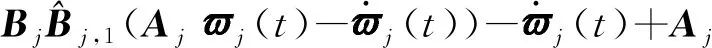
(48)
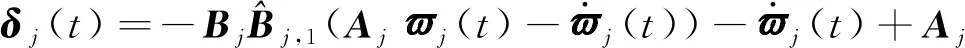
βjBjHjfj(t)
(49)
如果假设4和假设5成立,根据式(4)、式(6)和算法1中的步骤4可将式(49)进一步化简为
(50)
考虑下列Lyapunov函数:
(51)
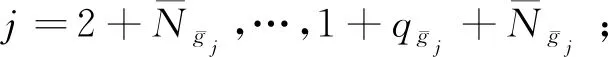
(52)
式中:

(53)
令
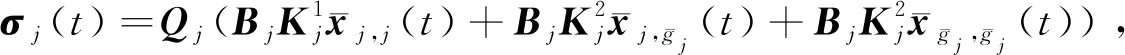
(54)
将式(53)和式(54)代入式(52)中,并根据式(51)可得
(55)
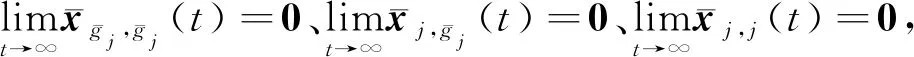
综合上述2种情况并根据定义1可知,异构多智能体系统能够实现在有向拓扑条件下的分组输出时变编队跟踪控制。证毕。

3 数值仿真
为了更贴合工程实际背景,考虑由1个虚拟领导者、10架无人机、5辆无人车组成异构多智能体系统完成空地协同搜索任务,其中2架无人机与1辆无人车为分组领导者,其余为跟随者。根据文献[22]可知,四旋翼无人机模型的系统矩阵可近似为同理根据文献[23]可知,麦克纳姆轮无人车模型的系统矩阵可近似为AR=0、BR=1、CR=1。虚拟领导者的模型也采用文献[22]中的无人机模型。
事实上,本文所研究的方法可以适用到任意可近似线性化的物理模型中。为了获得更加直观性的验证效果,仿真中考虑异构多智能体系统在三维惯性空间的运动。虚拟领导者的初始位置设定在(-4,0,0),在OX轴、OY轴和OZ轴方向上的初始速度分别设定为0、-4和0。10架无人机和5辆无人车在OX轴和OY轴方向上的初始位置在(-5,5)中随机选取,在OZ轴方向上的初始位置和各轴方向上的初始速度为0,即模拟无人机和无人车由静止状态进行空地协同搜索的过程。
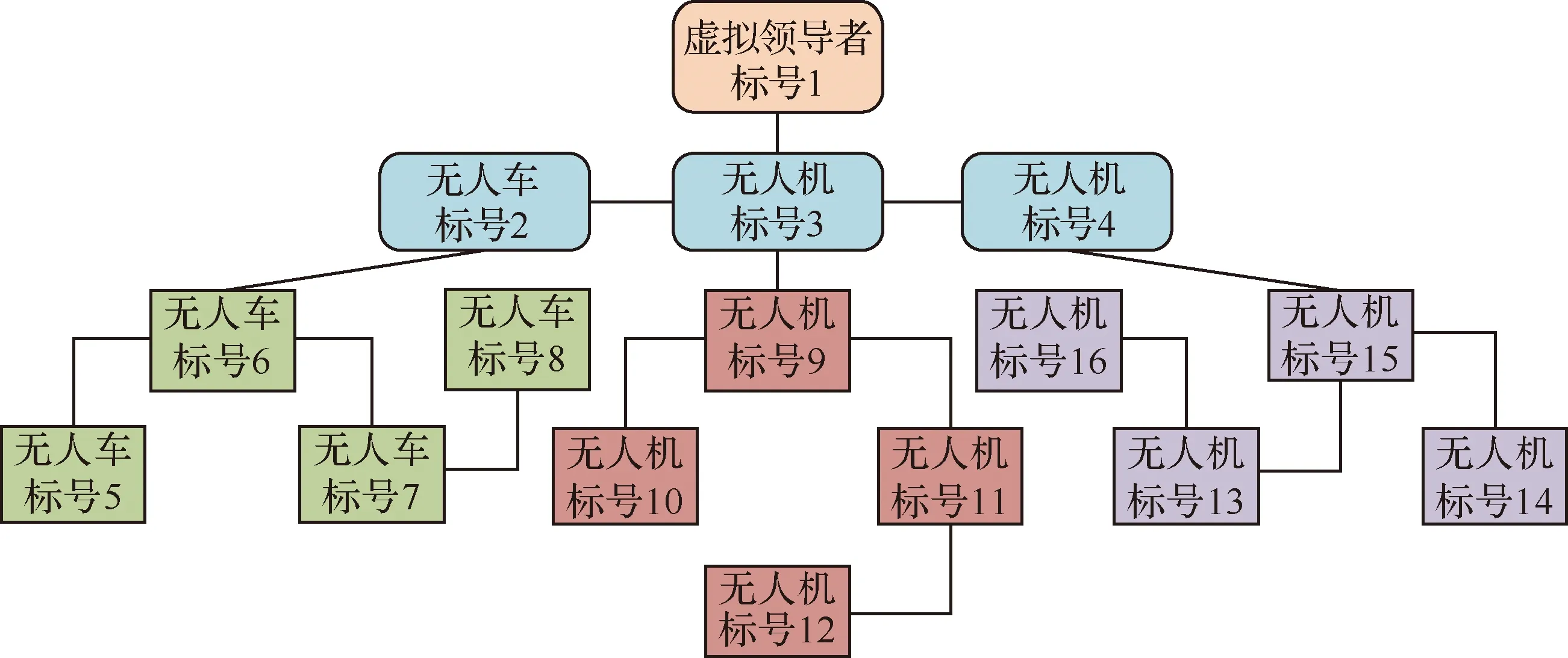
图1 异构多智能体系统模型架构示意图Fig.1 Model structure of heterogeneous multi-agent systems
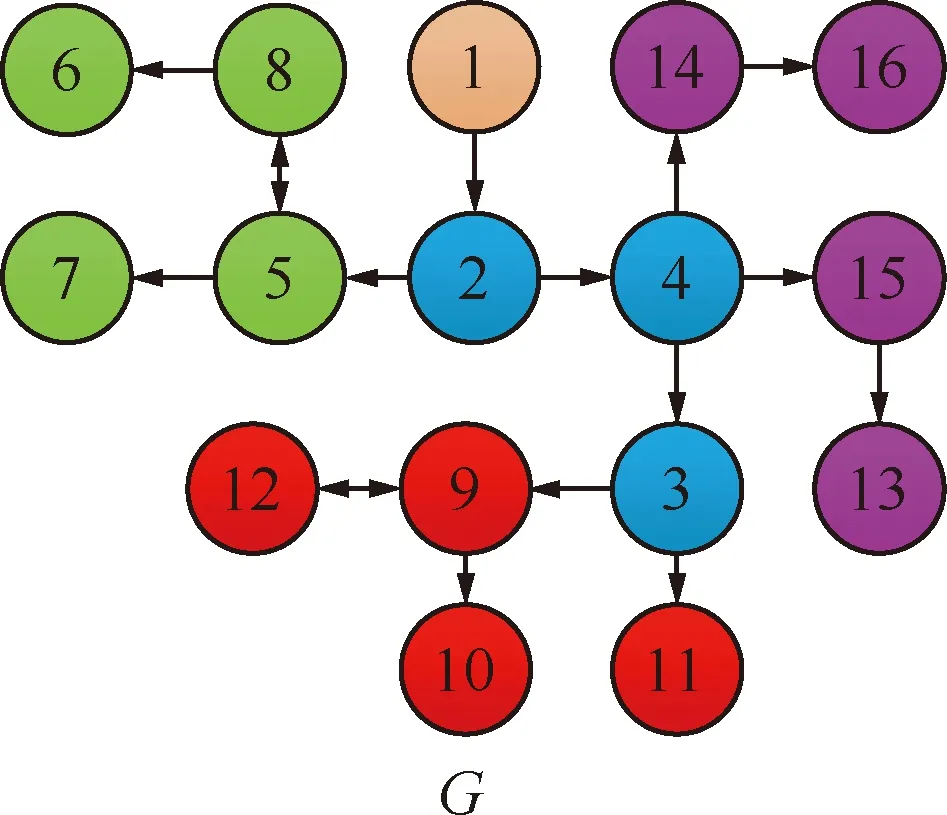
图2 异构多智能体系统通信拓扑关系Fig.2 Interaction topologies of heterogeneous multi-agent systems



根据算法1、算法2和算法3,得到以下参数值:
αi=10i=2,3,…,16
βi=10i=2,3,…,16
E2=[1, 0],Ei=1i=5,6,7,8
Ei=I2i=3,4,9,10,…,16
F2=[0, 1],Fi=0i=5,6,7,8
Fi=[0, 0]i=3,4,9,10,…,16
H2=0,Hi=1i=3,4,…,16
Si=-1i=2,5,6,7,8
Si=[-2,-1]Ti=3,4,9,10,…,16

P2=1
整个多智能体系统的搜索轨迹如图3中虚点所示,图中还包括虚拟领导者,无人机和无人车在t=0, 8, 16 s时的位置信息,其中虚拟领导者用黑色星号表示,一组无人机用实心五角形表示,另一组无人机用实心六角形表示,无人车用实心圆来表示,区别是作为分组领导者的无人机和无人车用蓝色表示,作为跟随者的无人机和无人车用其他颜色表示。从图3中可以看出,2个无人机分组维持定高搜索前进,无人车分组沿地面搜索前进,无人机分组与无人车分组之间形成空地协同搜索态势。图4给出了异构多智能体系统在惯性空间各轴分量的分组编队跟踪误差,定义为
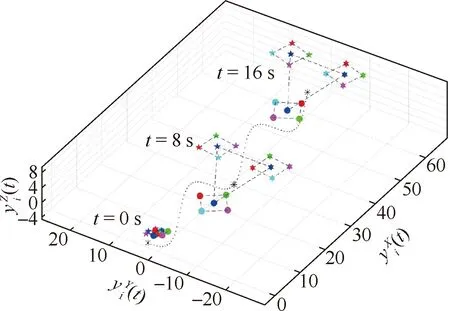
图3 异构多智能体系统的搜索轨迹与各智能体部分时刻的位置信息Fig.3 Trajectory and position at certain time of heterogeneous multi-agent systems
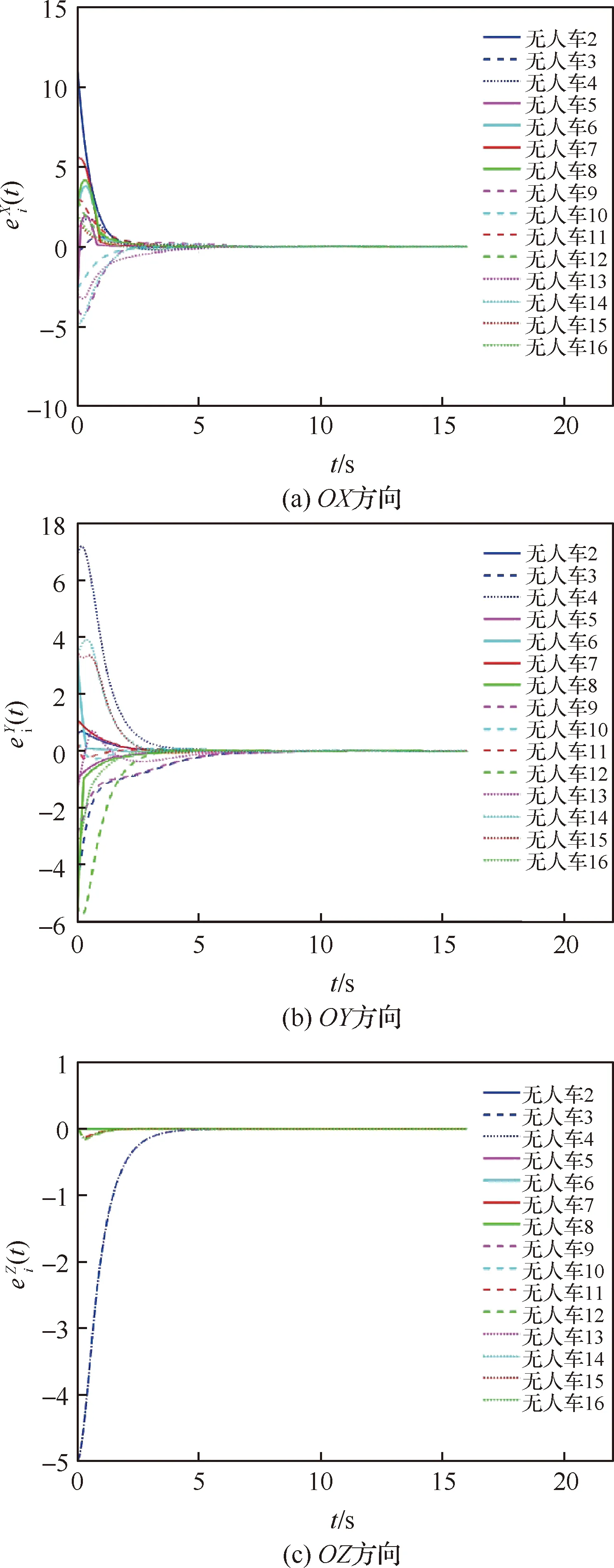
图4 异构多智能体系统在惯性空间各分量的分组输出时变编队跟踪误差Fig.4 Tracking errors of time-varying output group formation of heterogeneous multi-agent systems in inertial space
ei(t)
从图4中可以看出,编队跟踪误差在惯性空间OX、OY、OZ轴方向上的分量大约于6 s后全部收敛到0。因此仿真结果验证了本文所研究的方法能够使异构多智能体系统实现分组输出时变编队跟踪控制。
4 结 论
本文研究了高阶异构多智能体系统在有向拓扑条件下的分组输出时变编队跟踪控制问题。在集群系统中智能体的动力学模型完全不同的情况下,基于邻居间的相对信息、观测器理论和滑模控制理论,分别设计了针对分组领导者和跟随者的控制协议。通过理论证明和仿真验证结果表明,上述控制协议能够使异构集群系统实现分组时变编队跟踪控制,因此本文给出的方法具有良好的理论价值和工程应用价值。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

