基于支持向量机的太阳磁场活动区极性反转线位置的探测∗
王 强 郑 胜 邓元勇 黄 宇黎 辉 甘为群 苏江涛,3
(1三峡大学计算机与信息学院宜昌443002)
(2中国科学院国家天文台北京100101)
(3中国科学院大学北京100049)
(4中国科学院紫金山天文台南京210023)
1 引言
太阳的活动现象十分丰富,其中太阳耀斑和日冕物质抛射是两类最剧烈的爆发现象.太阳耀斑是局部区域突然快速释放大量能量的过程.耀斑爆发时释放的大量高能离子对地球空间环境破坏性较大,尤其是影响航空航天与导航通信行业.对太阳活动现象的研究是天文研究领域的一个重要方向.太阳活动区磁场极性反转线的位置,长期以来一直是太阳活动观测和理论研究的核心特征.
为了理解太阳耀斑的物理机制和开展研究耀斑预测的方法,最重要的是找到与耀斑触发相关的临界磁场特征.许多研究发现,强磁场区域的极性反转线在耀斑活动中起着重要作用.Sadykov等[1]分析了纵向磁场特征与太阳耀斑之间的关系,研究证实了极性反转线活动区特征在耀斑预报过程中的独特作用,并证明了仅使用纵向磁图进行耀斑预报的可能性.Cui等[2]从大量迈克尔逊多普勒成像仪(Michelson Doppler Imager,MDI)纵向磁图中,计算了描述光球磁场特性的最大水平梯度、中性线长度和奇点数3个物理量,并拟合出了耀斑产生率与特征因子之间存在着S型函数的关系.他们的结果表明,太阳耀斑的产生率随着磁场非势性和复杂性的增加而增加.Yang等[3]的研究指出在耀斑之前沿着活动区的磁性中性线出现很强的剪切流动.Victor等[4]使用太阳磁场的极性反转线(Polarity Inversion Line,PIL)长度、PIL附近的强磁场区域面积以及该区域的总通量作为太阳耀斑预测的特征,并获得了良好的短期预测结果.Sharykin等[5]的观测结果证明了位于色球层等离子体中的主要能量释放位置在具有强电流集中的PIL附近.开发用于检测极性反转线的方法为提高观测数据使用效率、快速监测太阳活动水平、改善空间天气预报有着积极作用,同时也是一种提高我们对太阳上这些爆发现象认识的方法.
极性反转线位置通常由研究者根据研究经验人工绘制,或简单使用等高线方法大致描绘.目前存在着几类极性反转线自动检测方法,简介如下:
基于像素空间卷积类方法.Volobuev等[6]使用一种元胞自动机的最近邻检测技术,考虑磁图的每个像素及其周围的8个邻域,若中心像素值与周围邻域像素值符号异号,则将其归为极性反转线上的像素.使用这个逻辑规则通过模板遍历全图找到所有极性反转线集合.同样,Steward等[7]将原始图像逐个像素乘以从原始图像向右移动一个像素获得的新图像,当乘积结果发生异号并且大于一定的梯度阈值则归为极性反转线上的像素.对向上方向移动一个像素执行相同的步骤,合并像素集获得最终的极性反转线.虽然此类方法较为简单易于实现,但从结果来看这些检测的极性反转线像素点较为零碎,受噪声干扰较大.
基于梯度技术类检测方法.Schrijver[8]为了识别强梯度的极性反转线,首先对MDI磁图构造了二元正、负强磁场位图,然后使用3×3的核进行膨胀以创建膨胀的正负位图,两幅膨胀后的位图的乘积不为零时被识别为强场区域的极性反转线.Welsch等[9]使用Schrijver[8]的梯度检测技术探索了关于极性反转线附近强磁场梯度的起源,他们的结果表明新的磁场浮现确实可以导致强磁场梯度,但不是必要条件.
基于形态学扩张技术类的检测方法.Sadykov等[1]使用最早由Victor等[4]提出的磁图分割的方法,将磁图划分为强正场、强负场和弱场(“中性”段)的区域.首先使用高斯滤波器对原始磁图进行平滑处理并应用分割算法.然后,分别对正负区域应用形态学扩展程序,将正负片段扩张后的交集作为极性反转线集合.最后,我们过滤掉像素数少于一定数目的碎片.
这3类方法都存在着极性反转线像素点较为细碎、不连续、受噪声影响较大等问题.本文从支持向量机(Support Vector Machine,SVM)的模型出发,将极性反转线位置的探测问题转化为模式识别中二分类问题.提出了一种基于支持向量机的极性反转线检测算法,自动探测与识别太阳动力学天文台(Solar Dynamics Observatory,SDO)日震和磁成像仪(Helioseismic and Magnetic Imager,HMI)磁图的极性反转线位置.测试结果表明,此算法可以精确有效地检测太阳活动区的极性反转线.
2 算法原理
支持向量机是一种典型的二分类模型[10],主要用于模式识别中的分类问题.其基本思想是在特征空间中寻找一个最佳分割超平面,使得这个超平面能将样本正确分类并且分类间距达到最大.支持向量机的一个关键概念就是引入了分类间隔,分类问题最终就可转化成约束优化问题求解.对一确定样本,给定样本点集合D={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{−1,+1}.m为样本点个数.分类超平面可由下面表达式描述:

其中的w为超平面的法向量,描述了分割超平面的方向信息,b为位移,x为样本点.超平面由(w,b)唯一决定.样本空间中的任一点x到超平面的距离可表示为:

有了超平面和分类间隔的描述就可以确定一个分类器了.假设分割超平面能将样本正确划分,对于(xi,yi)∈D,二分类器描述为:
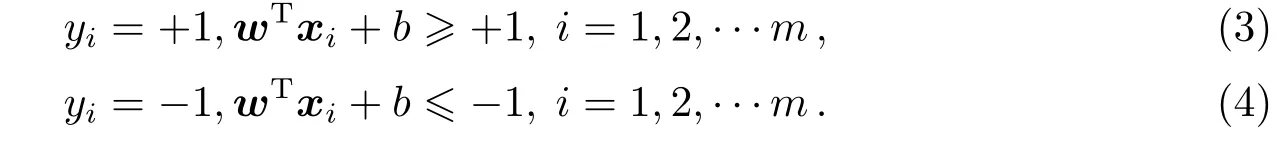
即:

距离超平面最近的点使得等号成立,叫做“支持向量”.两个异侧支持向量到超平面距离之和称为间隔γ,用下式表示:

要找一个划分超平面能将样本正确分类并且分类间隔达到最大,也就是找到(w,b)使其(5)式分类器成立,即:
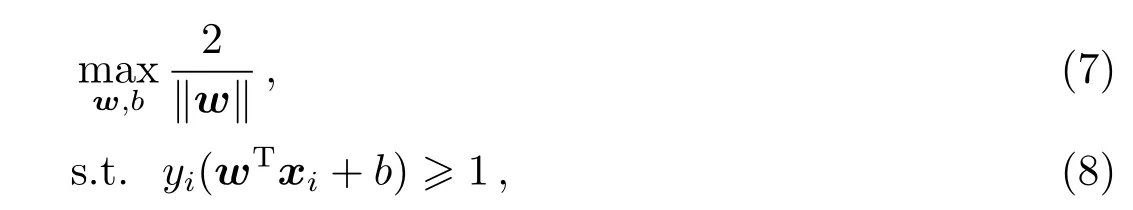
支持向量机基本型便可写为:
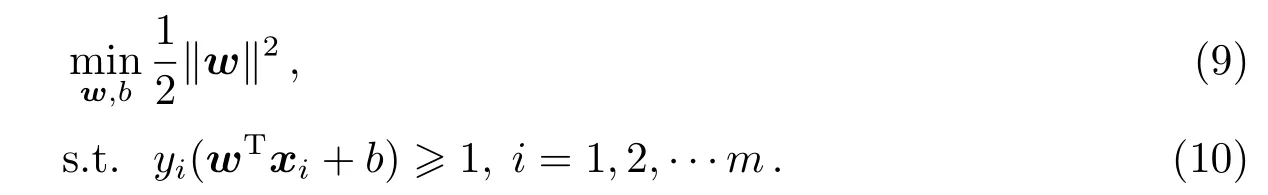
在实际应用中还存在错误分类的问题,仅通过最大间距找到决策边界是不够的,还需要考虑错误分类的情况.因此需要一个惩罚因子C,增强模型的容错能力.它在优化函数里主要是平衡支持向量的复杂度和误分类率这两者之间的关系.
实际问题中,我们的数据在原始样本空间中并不一定线性可分,无法找到这样一个线性超平面将样本正确分类.对于线性不可分问题,SVM使用一种叫做“核函数”的技术,将原始线性不可分低维空间映射到一个更高维度特征空间使其线性可分.
设φ(x i)为映射后的特征向量,则非线性优化问题转化为:

其中φ(x i)为低维到高维的映射核函数.常用核函数见表1.

表1 常用核函数及其表达式Table 1 Com m on ker nel functions and their ex p ressions
表中,x j为D中样本点,d为多项式次数,σ是高斯核函数带宽,tanh为双曲正切函数.β、θ为根据实验人工设置的参数,β是分类类别的倒数,θ是偏移量.
本文提出的基于支持向量机的极性反转线检测算法,关键在于如何转换成二分类问题,下面将详细描述具体算法流程:
步骤1:待检测区域截取,活动区的截取直接使用鼠标点选的方式;
步骤2:对截取后的图像进行预处理,包括平滑去噪等;
步骤4:SVM输出,将每个像素点值的正负代数符号转换成输出标签,用+1或者−1表示;
步骤5:核函数映射,选取径向基函数(Radial Basis Function,RBF)作为核函数,映射到特征空间;
步骤6:超平面计算,通过选取的特征向量与标签利用SVM计算(1)式中的w与b;
步骤7:极性反转线位置确定,有了分割超平面参数w与b即确定了极性反转线位置.
本文算法的具体流程如图1所示.
3 实验过程
本文的实验数据来自于SDO/HMI,数据形式为FITS格式.图2所示为2017年9月5日NOAA12673活动区纵向磁图.我们以图像左上点为原点,从原点自左向右为X轴,自上向下为Y轴建立坐标系,图像分辨率大小为160像素×160像素.

图1 基于支持向量机的极性反转线检测算法流程Fig.1 Flow chart of p olarity inversion line detection algorithm based on supp ort vector machine
基于支持向量机的极性反转线检测算法具体实验流程如下:
(1)磁场活动区区域截取、图像去噪、平滑等预处理.
会上,中国农业大学教授、资源与环境学院副院长江荣风,安徽农业大学党委常委、副校长姚佐文,安徽六国化工副总经理、总工程师沈浩,代表三方签署战略合作协议。
从全日面的太阳磁场图像中截取所需要检测的局部活动区,然后,使用高斯滤波器对磁场图像进行平滑去噪处理,该操作能去除很多无关细碎的小块,保持极性反转线的连续性,增强检测结果的准确性与稳定性.
(2)二分类模型的转换.
将图像数据转换成可以输入到支持向量机模型中的向量.基于极性反转线的概念,极性反转线的位置只与正负磁极位置相关.具体做法是,遍历每个像素点,记录其图像坐标p(u,v)作为SVM特征向量输入.将每个像素点灰度值的正负代数符号转换成输出类别,用+1或者−1表示.因此输入向量为(u,v,±1).我们将大于一定阈值ϵ的像素归为正极性类,用+1表示,而将小于阈值ϵ的像素归为负极性类,用−1表示,这样就将转换成一个二分类问题.这里阈值ϵ的选择很重要,因为小的阈值将导致PIL的细碎离散片段增加,这些小的片段,对研究者并无实际用途.较大的阈值将不能正确完全检测PIL.在本实验中图像分辨率大小为160像素×160像素,通过大量实验,结果表明30–50 Gs能够取得较好效果.
(3)构建支持向量机模型.
模型构建根据支持向量机模型,定义规则,正极性类yi=+1,对所有正极性样本点以(u,v)表示,使得:
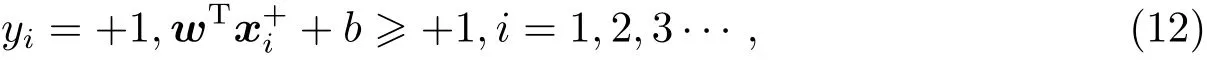
负极性类yi=−1,对所有负极性样本点以(u,v)表示,使得:

由于我们的数据线性不可分,需要选择一个合适的核函数.对于非线性可分的问题,高斯核函数也称为RBF核函数能够取得较好结果.高斯核如下式:

其中,高斯核σ参数取值与样本的划分精细程度有关:σ越大,低维空间中选择的曲线越复杂,分的类别越细,容易出现过拟合.σ越小,分的类别越粗,可能导致无法将数据区分开来,容易出现欠拟合.
给定C,增强模型的容错能力.它在优化函数里主要是平衡支持向量的复杂度和误分类率这两者之间的关系.当C比较大时,我们的损失函数也会越大,这样我们会有更多的支持向量,也就是说支持向量和超平面的模型也会变得越复杂,也容易过拟合.反之,当C比较小时,会选择较少的样本来做支持向量,最终的支持向量和超平面的模型也会简单.
(4)计算分割超平面,将决策边界在磁图中画出.
将第3步转换后的数据输入到支持向量机模型中,计算分割超平面求解(w,b)使(wTx+b)=1,将计算出的决策边界在磁图上画出.如图3所示是使用高斯核函数参数C=0.1,σ=0.05最终检测结果.

图2 2017年9月5日NOAA AR(Active Region)12673磁图Fig.2 Magnetograms of NOAA AR12673 on 2017 September 5
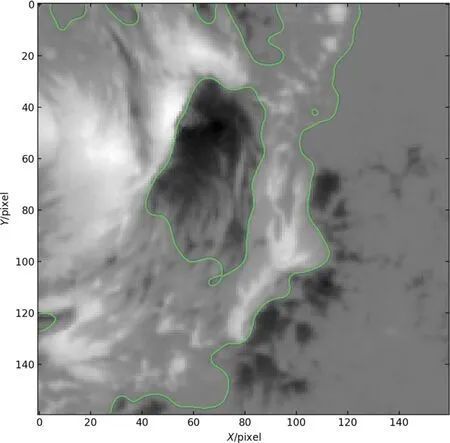
图3 NOAA AR12673磁图,绿色的线为阈值为30 Gs,使用高斯核函数参数C=0.1,σ=0.05极性反转线检测结果.Fig.3 Magnetograms of NOAA AR12673,the green line is the p olarity inversion lines detection result using a threshold of 30 Gs and a Gaussian kernel function parameter of C=0.1,σ=0.05.
根据研究者的目的不同,可以使用不同的参数控制检测的精细程度,如图4所示.
为了说明算法的有效性,我们对比基于像素空间卷积类方法,此方法也是较为常见的方法.对同样的数据,使用模板计算每个像素与其周围的4个邻域像素的卷积,若中心像素值与周围领域像素值符号异号,则将其归为极性反转线上的像素.使用这个逻辑规则通过模板遍历全图找到所有极性反转线集合,如图5所示为使用阈值为50 Gs的实验结果.
从检测效果来看,此方法虽然简单易于实现,但极性反转线像素点较为细碎,不连续,受噪声影响较大.使用不同的阈值时,检测结果会存在很大差异,例如使用稍小的阈值就会引入大量宁静区的污染像素,造成极性反转线统计结果有较大差异.同时对于不同的磁图,阈值选择无法统一标准,人为干预性较大.
极性反转线的长度通常是研究者所关心的问题,本文算法在检测结果上能较为直观地反映极性反转线的真实位置,同时极性反转线的连续性好.极性反转线长度可定义为极性反转线所占像素数之和.因此在后续计算极性反转线长度时可以在检测结果的基础上采用如上定义统计最长的极性反转线像素之和.

图4 NOAA AR12673磁图,绿色的线为使用阈值为50 Gs,高斯核函数参数为C=0.1,σ=0.1的极性反转线检测结果.Fig.4 Magnetograms of NOAA AR12673,the green line is the polarity inversion lines detection result using a threshold of 50 Gs and a Gaussian kernel function parameter of C=0.1,σ=0.1.

图5 NOAA AR12673磁图,绿色点为极性反转线上的像素.Fig.5 Magnetograms of NOAA AR12673,green colors show the pixels of p olarity inversion lines.
4 总结与讨论
本文从支持向量机的模型出发,结合极性反转线的特性,将极性反转线位置的探测问题转化为一个模式识别中的二分类问题.提出了一种基于支持向量机的有效算法,以太阳动力学观测台日震及磁成像仪磁图为实验数据检测极性反转线.实验结果表明,此算法可以有效检测太阳活动区的极性反转线,检测精度较高,检测结果也可叠加在同一区域不同波段的太阳图像上,便于研究者开展后续工作.另外,基于支持向量机原理,此方法也可推广至宁静区大尺度暗条极性反转线的检测.今后将会进一步优化算法应对全局区域的检测.

