ASO-S卫星基于太阳导行镜的高精度高稳定度姿态控制系统

陈炳龙 方禹鑫 邓 雷 杨文哲

(中国科学院微小卫星创新研究院上海201210)

1 引言

先进天基太阳天文台(Advanced Space-based Solar Observatory,ASO-S)卫星任务为同时观测太阳磁场、太阳耀斑和日冕物质抛射,以此研究当代太阳物理领域重大前沿科学问题—太阳磁场、太阳耀斑和日冕物质抛射3者之间的关系[1].为此,卫星总体对姿控分系统提出如下技术要求:非卫星-太阳方向的绝对姿态指向精度优于36′′、相对姿态稳定度优于7′′/60 s.借鉴国内外高精度、高稳定度卫星的先进经验[2–3],设计了星敏感器、导行镜和光纤陀螺为姿态敏感器、反作用轮为执行机构的偏置零动量三轴稳定姿态控制系统.与传统卫星姿态控制方案相比,本文提出了利用载荷望远镜之一的导行镜(GT)观测数据[4],即太阳中心偏离探测器测量坐标系的偏差角,引入卫星姿态控制闭环.与卫星-太阳方向垂直的坐标轴选用导行镜测量值进行定姿;与卫星-太阳方向平行的坐标轴选用星敏感器测量值进行定姿.最终实现卫星GT光轴指向太阳中心的高精度高稳定度控制.

2 坐标系定义与姿态描述

2.1 坐标系定义

(1)J2000坐标系

时刻在历元2000年1月1日12时(标准历元J2000.0)的地心惯性坐标系,记作O-XIYIZI(简称I系),基准平面是历元为J2000.0时的地球平赤道面.

O—地心;

OXI—指向此历元时的平春分点方向;

OZI—指向平北极;

OYI—在地球平赤道面上,与OXI和OZI构成右旋正交系.

在J2000坐标系中,恒星、太阳、月亮等天体的赤经、赤纬用(αI,δI)表示.地心惯性坐标系为卫星的飞行参考坐标系.

(2)瞬时平赤道坐标系

时刻为JD(Julian Day)历元的地心惯性坐标系,记作O-XI_JDYI_JDZI_JD(简称I_JD 系),基准平面是历元为JD时的瞬时平赤道.

OXI_JD—指向JD历元时的瞬时平春分点方向;

OZI_JD—指向瞬时赤道平北极;

OYI_JD—在瞬时平赤道面上,与OZ I_JD和OX I_JD构成右旋正交系.

(3)瞬时平黄道坐标系

时刻在JD历元的地心黄道坐标系,记作O-XEcI_JD Y EcI_JD Z EcI_JD(简称EcI_JD系),基准平面是历元为JD的瞬时黄道.

OXEcI_JD—指向JD历元的瞬时平春分点方向;

OZEcI_JD—指向瞬时北黄极;

OYEcI_JD—在瞬时黄道面上,与OZ EcI_JD和OX EcI_JD构成右旋正交系.

其中,R1(εA)为绕任意坐标系X轴转动εA的姿态转换矩阵;εA为瞬时平黄赤交角.

(4)卫星质心本体坐标系

记作OB-XBYBZB(简称B系).

OB—卫星质心;

OBXB—平行于星箭分离面,与莱曼阿尔法太阳望远镜(Lyman-alpha Solar Telescope,LST)中的白光望远镜光轴指向一致为正;

OBZB—垂直于星箭分离面,指向载荷舱方向为正;

OBYB—平行于星箭分离面,与OBZB、OBXB构成右旋正交系.

(5)GT测量坐标系

记作GT0系.

OGT—导行镜光轴在探测器平面的投影;

OGTXGT—与本体系OBXB平行;

OGTZGT—在探测器平面内、与星箭分离面垂直,由火箭指向卫星方向为正;

OGTYGT—在探测器平面内、与星箭分离面平行,按右旋正交系与OGTZGT、OGTXGT正交.

(6)姿态参考坐标系

为满足ASO-S卫星对日观测的指向要求(卫星-太阳连线方向无旋转),建立卫星指向参考坐标系O-XpYpZp(如图1所示,其中ε0为平黄赤交角),简称P系,定义如下:

OXp—平行于卫星质心与太阳中心连线,指向太阳方向为正;

OYp—与I系瞬时北黄极单位矢量(记作ZEcl_I)叉乘OXp单位矢量得到的矢量方向平行;

OZp—与OXp和OYp构成右旋正交系.

北黄极计算过程详见4.2节.卫星姿态控制系统使卫星质心坐标系始终与指向参考坐标系重合即可满足对日观测的姿态指向需求.

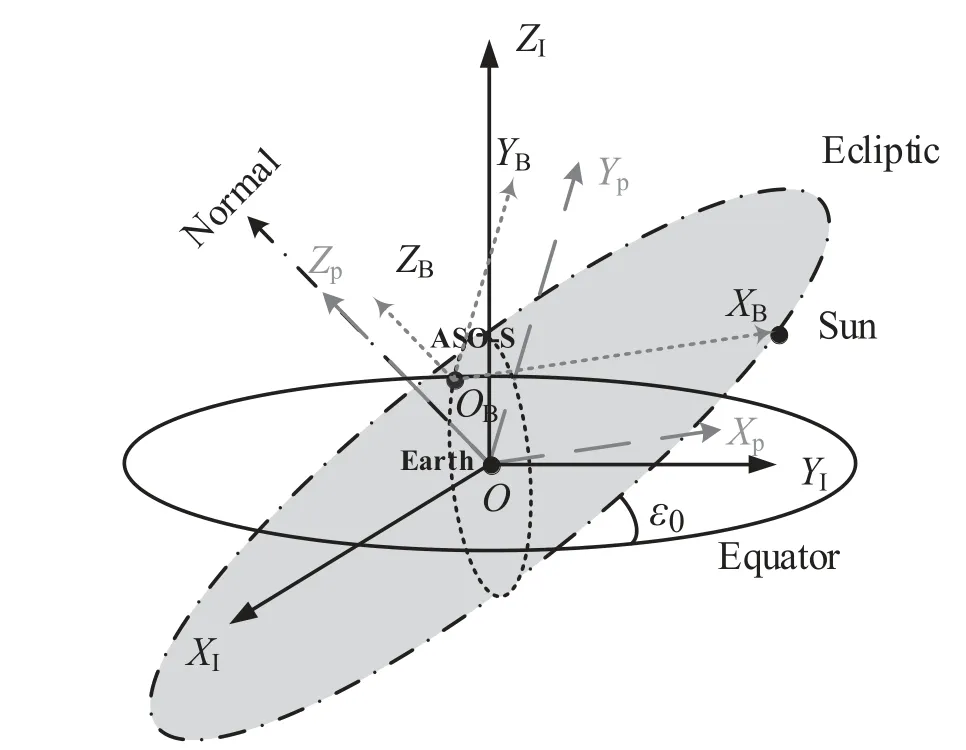
图1 卫星指向参考坐标系Fig.1 Pointing reference coordinate system for satellite

2.2 姿态描述

(1)四元数

四元数是具有4个元素的超复数,它可以描述一个坐标系或一个矢量相对于某一坐标系的旋转,定义为其中,q0=cos(0.5ϕ),qv=[q1,q2,q3]T=e sin(0.5ϕ);e表示旋转轴方向单位矢量,ϕ表示旋转角.

(2)欧拉角

卫星质心坐标系相对于参考坐标系(P系)的夹角定义为姿态角,用3-1-2转序对姿态进行数学描述,以欧拉角φ、θ、ψ分别表示滚转角、俯仰角和偏航角.按照旋转次序,变量表示为:

ψ:偏航角,绕ZB轴;φ:滚转角,绕XB轴;θ:俯仰角,绕YB轴.

B系相对P系姿态四元数qpb可表示为P系相对I系姿态四元数qip的逆与B系相对I系姿态四元数qib的乘积,算法如下:

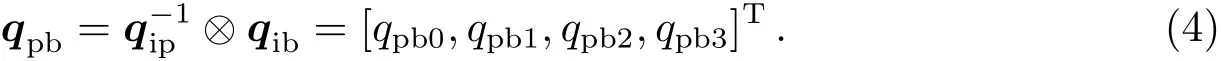
3 太阳导行镜

3.1 工作原理

导行镜由滤光片、同轴光学系统、二极管阵列探测器组成.太阳辐射经过653 nm滤光片滤波后进入导行镜成像光学系统,再照射到焦面上的四象限光电探测器上.当太阳像偏离二极管阵列探测器中心时,光电二极管接收到的信号将不平衡,对采集的四象限光电二极管偏差信号进行计算和处理,获得太阳指向角度变化信号.光电二极管采集太阳边缘信号精度可达0.1′′,可以保证LST对日指向稳定性优于0.6′′/60 s,指向精度优于10′′.

导行镜输出值为经过无量纲化处理的太阳中心相对探测器测量系原点的偏差角,记作δy、δz.当数值为−1至+1区间时,表示太阳中心位于导行镜线性区域(约60′′);当太阳中心超出线性区域时,导行镜输出数据为固定值±1.25:当太阳中心位于+YGT或+ZGT方向时输出+1.25,当太阳中心位于−YGT或−ZGT方向时输出−1.25;当太阳中心超出导行镜的测量范围0.15◦时,导行镜输出数据为固定值+1.5.

3.2 数学模型

太阳辐射在探测器上形成圆形光斑S′点,当入射光角度发生变化时,光斑中心在YGTOGTZGT平面内移动,如下图2所示.

在GT0坐标系下,太阳光线与GT光轴交点F的坐标为(f,0,0)(f为GT光路焦距)、S′点坐标为(0,y,z),则太阳矢量可表示为(f,−y,−z).

太阳中心偏差角α、β可表示为:tanα=y/f、tanβ=z/f.

在导行镜线性区域60′′范围内,导行镜输出的无量纲数据与α、β关系为:α=Kyδy、β=Kzδz(系数Ky和Kz可在地面进行定标后给出,单位:角秒).

进行如下简化:tanα≈α、tanβ≈β(tan(60′′)与60′′有7位有效数字相同),S′点坐标值y、z可表示为y=αf、z=βf.此时,太阳矢量可表示为(f,−αf,−βf).归一化得:[1/H,−α/H,−β/H]T,其中

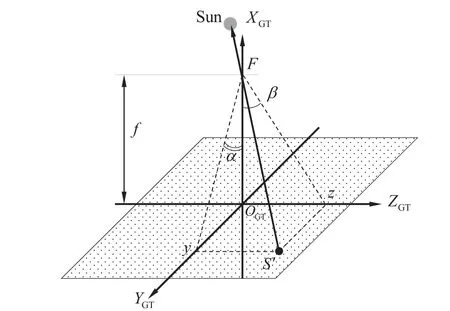
图2 导行镜数学模型示意图Fig.2 Schematic diagram for guide telescop e model

4 对日观测导引律

4.1 太阳位置计算

选用美国喷气动力实验室(JPL)的行星/月球历表DE430/LE430,用切比雪夫多项式存储历表位置.为简化计算量,仅计算太阳、地月系质心、月球3项数据,时间跨度是2021至2029年.由此历表计算得到质心力学时儒略日(记作JDTDB)时刻ICRF(International Celestial Reference Frame)下太阳质心相对太阳系质心位置矢量Psun、地球质心相对太阳系质心位置矢量PE和速度矢量VE.

ICRF系转换至J2000系转换矩阵量AI_ICRF可表示为:

考虑光行时和光行差效应对指向的影响:用迭代计算法得到光行时修正后太阳位置矢量Ssun_lt;用洛伦兹变换方法计算修正光行差后的太阳位置矢量Ssun_lt_s.

4.2 瞬时北黄极计算

IERS(International Earth Rotation Service)规范2010年推荐岁差部分采用4次旋转的岁差矩阵,避免3次旋转岁差矩阵在J2000.0历元附近对岁差参数敏感的问题.本文使用Fukushima-Williams方法[5],岁差矩阵P(表示由J2000历元I系至任意JD历元I系的姿态转换矩)计算如下:

其中,R3()表示绕任意坐标系Z轴转动某角度的姿态转换矩阵;ΨJ2000、ϕJ2000、γJ2000为3个岁差角(单位:角秒).

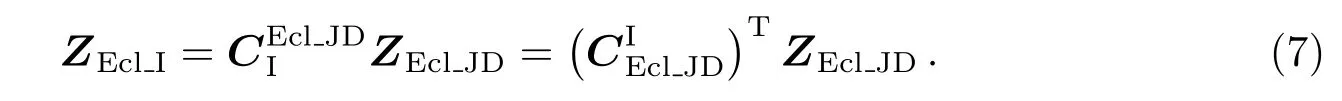
4.3 期望姿态四元数

(a)计算P系各坐标轴单位矢量在J2000历元I系的表示形式

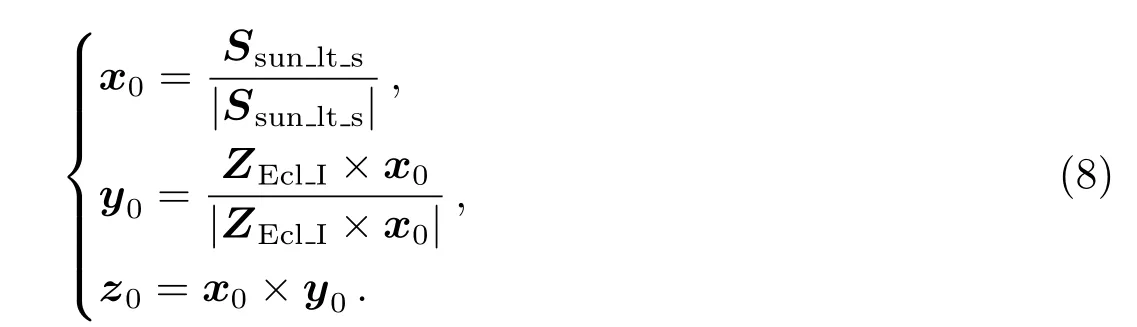
(c)由姿态转换矩阵计算四元数qsun,即为期望姿态四元数.

5 姿态控制器设计与仿真验证

5.1 导行镜测量值计算姿态偏差

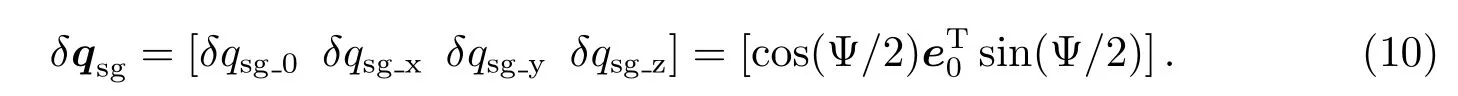
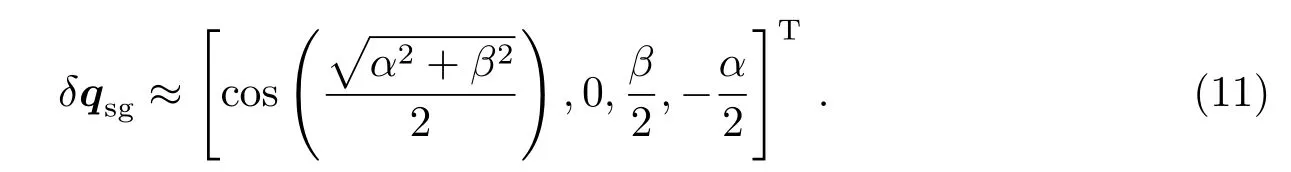
5.2 星敏感器测量值计算姿态偏差

计算qi_b与期望四元数qsun之间的偏差

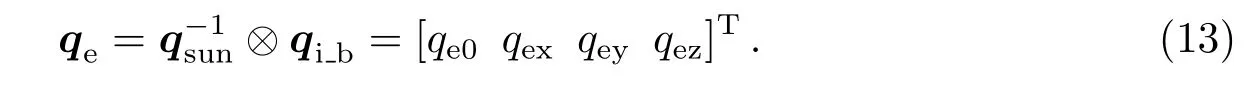
若qe0<0,则qe=−qe.

5.3 PID控制器设计

以陀螺测量值做为当前卫星的姿态角速度值,记作ωi_b;期望姿态角速度记作ωexp=[0 0 0]T.定义偏差姿态角速度为:.卫星姿态动力学表示为

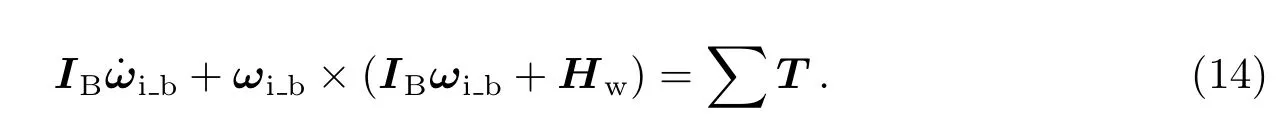
其中,IB为整星转动惯量、Hw为反作用轮组角动量、T为卫星受到外部力矩.

考虑ASO-S卫星轨道高度下的环境干扰力矩,例如重力梯度力矩、太阳光压力矩、气动力矩、剩磁干扰力矩等.

依据整星惯量数据,对日定向三轴稳定条件下重力梯度干扰力矩在6×10−4N·m量级;依据星体外形尺寸估算太阳光压力矩为1.0×10−6∼1.0×10−5N·m量级;依据720 km高度大气密度估算气动干扰力矩为1.0×10−6N·m量级;依据轨道高度地磁强度及星体剩磁矩估算剩磁干扰力矩为1.0×10−5N·m量级.综上所述,本文仅考虑数值最大的重力梯度力矩作为整星的干扰力矩.

以PID控制算法计算控制力矩Tc,如下

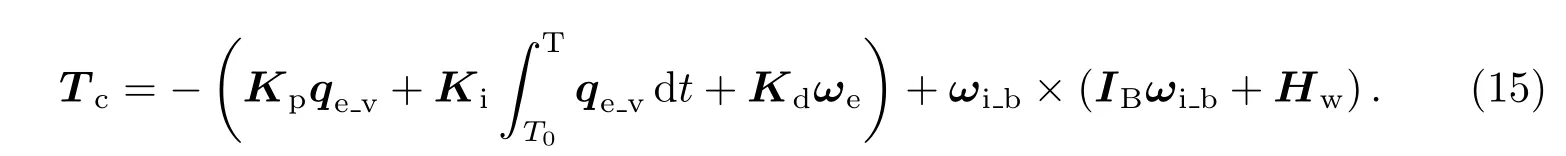
其中,Kp为比例项系数、Ki为积分项系数、Kd为微分项系数.为偏差四元数矢部、T0为积分初始时刻、T为积分终止时刻.

为实现卫星平台高精度、高稳定度对日观测指向,为反作用轮设置合适的中心转速,建立整星零动量稳定控制.当导行镜数据在[−0.9,0.9]时,以α=Kyδy、β=Kzδz计算偏差角;当导行镜数据为±1.25时,以α=200sign(δy)、β=200sign(δz)计算偏差角(α、β单位均为角秒).此时,偏差四元数矢部表示为

当导行镜数据为1.5时,只以星敏感器测量值计算偏差四元数矢部,可表示为

5.4 仿真分析

以Matlab-Simulink进行数学仿真,设置仿真参数.

星上时间(北京时间):2022年4月1日05:56:21.0;

轨道参数:半长轴as=7098140 m;偏心率es=0.001;轨道倾角is=98.39◦;升交点赤经Ωs=98.9◦;近地点幅角ωs=274.6◦;真近点角θs=179◦.

卫星转动惯量参数:

敏感器测量精度:星敏[3.5′′3.5′′28′′]T(3σ);陀螺5.0×10−5◦/s(3σ);导行镜YGT和ZGT方向0.1′′(3σ).

初始期望姿态四元数:[0.9756694−0.1978107−0.05409463 0.07754985]T;

B系相对I系的姿态四元数和角速度初值:qbi_0=[0.9749 0.2009−0.0210 0.0937]T、

PID参数:

4台反作用轮(RW1、RW2、RW3、RW4)参数:

最大输出力矩0.215 N·m;

初始转速[−500 500−500 500]Trpm(round per minute);

仿真时间:500 s.

分别使用星敏感器三轴定姿数据引入控制器和导行镜YGT/ZGT测量值+星敏感器XB轴定姿进行对比仿真,试验结果如图3和图4所示.其中:(a)、(b)分别为反作用轮转速和输出力矩,均无饱和现象;(c)为陀螺测量三轴姿态角速度、(d)为导行镜测量值,由无效值1.5逐渐收敛至线性区间[−0.9,0.9],最终趋近为0;(e)为绝对姿态控制精度;(f)为相对姿态稳定度.

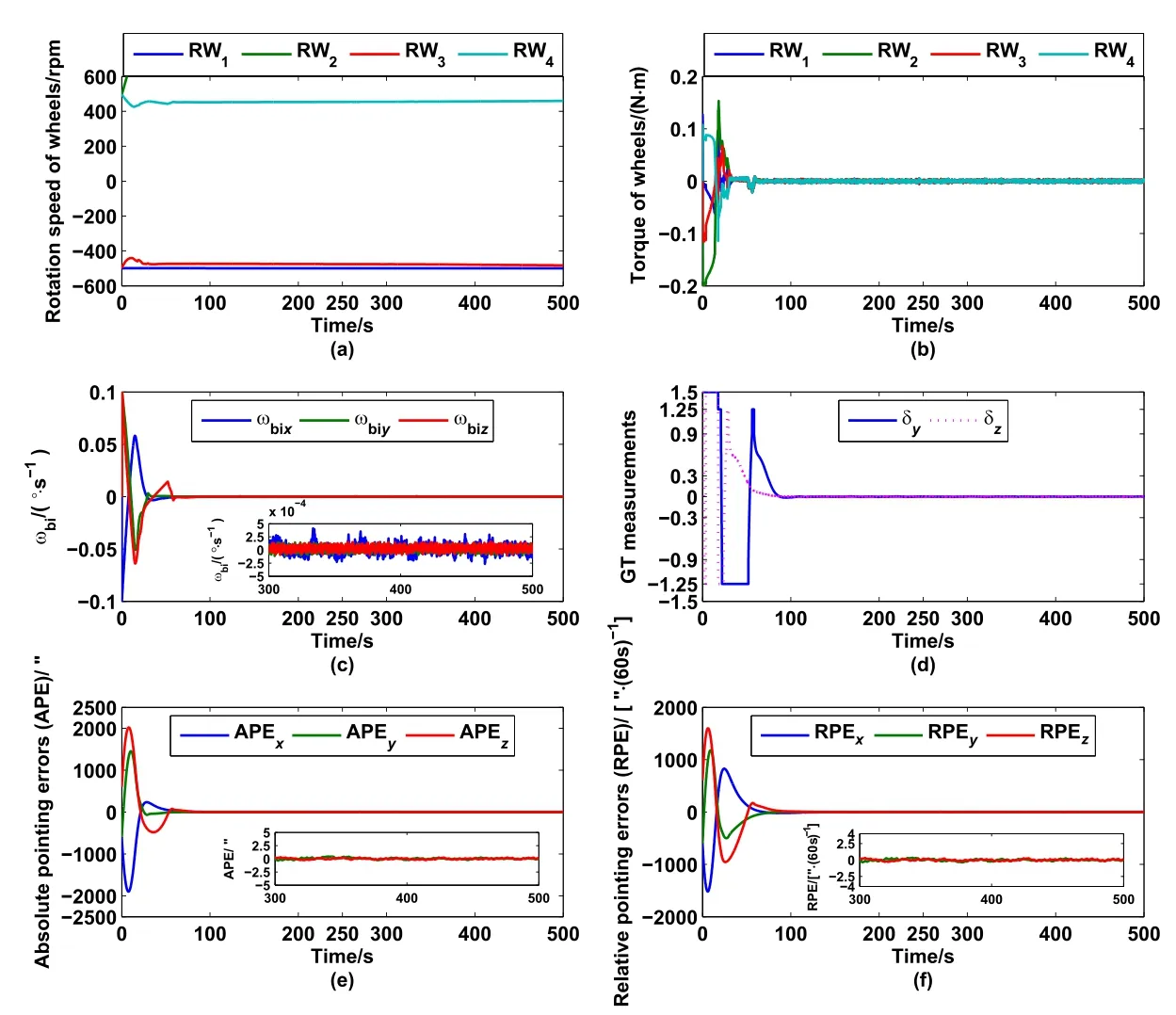
图3 星敏感器+导行镜定姿的闭环控制仿真结果Fig.3 Simulation results of closed-loop controller with attitude determination by star sensor and guide telescope data

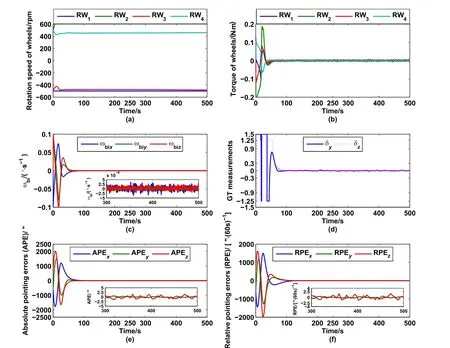
图4 星敏感器定姿的闭环控制仿真结果Fig.4 Simulation results of closed-loop controller with attitude determination by star sensor data

经过数据分析,得到如下结论:仅使用星敏感器定姿数据时,三轴姿态指向精度为[2.9254,0.6907,2.0477]′′、相对稳定度为[2.6110,0.6305,1.9088]′′/60 s;使用导行镜YGT/ZGT轴定姿数据、星敏XB轴定姿数据时,三轴姿态指向精度为[2.9774,0.4802,0.3391]′′、相对稳定度为[2.7403,0.4159,0.3382]′′/60 s.

综上分析,利用导行镜数据引入姿态控制闭环,可以显著提高卫星YB、ZB轴对日指向精度.对比仅使用星敏感器定姿的控制效果,导行镜闭环控制的绝对指向精度优于2′′、相对姿态稳定度优于1′′/60 s,满足ASO-S卫星技术指标要求.

6 结论

ASO-S卫星姿控分系统利用LST配备的GT测量载荷光轴与太阳中心的指向偏差,将其引入姿态控制器:利用星敏+陀螺定姿确定卫星-太阳方向控制偏差、GT测量值确定非卫星-太阳方向指向偏差,实现指向太阳中心的高精度高稳定度控制.数学仿真结果表明,该控制方法可以满足ASO-S卫星高精度高稳定度对日指向要求.