ASO-S/HXI太阳指向镜算法研究∗

喻福 苏 杨 张哲 黄 宇

(1中国科学院紫金山天文台南京210023)

(2中国科学技术大学天文与空间科学学院合肥230026)

(3中国科学院暗物质与空间天文重点实验室南京210023)

1 引言

先进天基太阳天文台(Advanced Space-based Solar Observatory,ASO-S)是中国首颗太阳专用观测卫星[1],硬X射线成像仪(Hard X-ray Imager,HXI)作为其3台载荷之一,主要负责在30–200 keV能段对耀斑源区进行成像、能谱和光变观测,以研究耀斑磁重联中的能量释放和高能电子加速等物理过程[2].由于在该能段上仅能看到耀斑区域,而无法获得全日面像,因此无法获知源区在日面上的位置.因此太阳指向镜作为HXI的组成部分,可实现对太阳中心位置的精确测量,提供指向中心坐标,并结合平台的旋转指向,以便对耀斑X射线源进行定位[2].指向镜的本质在于使用CCD(Charge-coupled Device)/CMOS(Complementary Metal Oxide Semiconductor)探测器对太阳进行可见光成像,再将得到的太阳光斑像近似为圆形,进而对圆的中心和半径参数进行计算.太阳在可见光的辐射主要来自光球,其边缘附近的辐射强度随日心角距增加变化非常陡峭,形成锐利的太阳边缘[3],这有利于提取太阳像的圆形轮廓特征.

HXI太阳指向镜的原理与太阳导行镜[4–5]相似(但无需反馈环节),都需计算日面中心在探测器视场中的坐标位置,或者相对偏移量.而太阳望远镜的导行模式主要经过了点、线、面的发展过程[6–8].在20世纪90年代以前多采用以太阳边缘对称的4个点来导行跟踪的四象限探测器法,如早期的怀柔多通道望远镜[6];到80年代以后线阵探测器技术逐渐完善,德国GCT[9](Gregory Coud´e Telescope)、日本Yohkoh[10]和美国RHESSI[11–12](Reuven Ramaty High Energy Solar Spectroscopic Imager)均采用此方法.特别需要指出的是,正是由于RHESSI对指向(日面边缘)的高精度测量,为了解太阳的实际形状提供了最精确的结果[13].而今随着计算机处理能力的提高,面阵探测器得到广泛使用,如SOHO[14](Solar and Heliospheric Observatory).面阵探测器的优点在于能够获取更多太阳的信息以及利用图像处理技术,更精确地反演日面中心位置.例如文献[7]提到的全日面像相关算法和质心算法,测试显示其在x和y方向检测精度的均方差分别约为0.0271′′和0.0101′′与0.1142′′和0.0828′′.

根据设计要求(来自《先进天基太阳天文台卫星(ASO-S)硬X射线成像仪初样设计报告》,2019年,文件编号KX-07-HXI00-JB-04),HXI太阳指向镜中心位置的测量精度要优于2′′.由于定位精度越高,越有利于多波段的数据分析,因此我们在本文中设定测试目标精度为1′′.由于数据量、采样率等方面的要求和限制条件,我们无法下传所有的图像.为了节省在轨计算资源和减少传输的数据量,提出了四象限法和边缘拟合法两种独立又可以结合的测量方法.为此,CMOS探测器每次曝光完成后,太阳指向镜将对图像进行在轨二值化处理,再采集两种数据下传,分别是14行数据和4个边角的面积,而中心坐标的计算在地面完成.其中,指向镜在轨记录的14行像元值用于获得太阳边缘,再利用最小二乘法进行拟合,得到太阳中心参数.而CMOS 4个正方形边角区域记录的像元值为1的数量,用于四象限法的计算.本文中,我们利用MATLAB软件和SDO(Solar Dynamic Observatory)/AIA(Atmospheric Imaging Assembly)[15]4500˚A Level 1.0的数据主要针对算法本身进行了测试和评估.

2 太阳指向镜测量原理

太阳指向镜的镜头部分安装在HXI载荷准直器框架的前基板上,焦距f≈1200 mm[2].当HXI对太阳观测时,太阳光斑成像如图1所示.其中,正方形ABCD为尺寸2048×2048 pixel的CMOS探测器,太阳光斑像的尺寸与CMOS的尺寸相当,如红色圆所示.然而地球绕日公转轨道为椭圆,近日点为1.471×108km、远日点为1.521×108km[3],且太阳半径为696342 km[16].因此,太阳视直径随地球绕日公转轨道变化最大为32.55′,最小为31.48′,这会导致在CMOS上的成像随之变化.再考虑到HXI指向镜光轴相对于平台指向的最大偏差(约为142 pixel)等因素,对应在CMOS上成像光斑的边缘被限制在绿色和黄色圆之间,对应的半径分别为Rmax=1174.6 pixel和Rmin=857.1 pixel.平行于x轴的14条红色虚线与太阳像边缘的交点作为边缘拟合法的数据点.4个边角上正方形的边长被选为L=445 pixel,从而保证太阳像无论如何移动(在设计安装误差范围内),太阳边缘都与4个区域的内边长有两个交点.正方形阴影区被二值化并分别求和后,理论上对应于图1中深色区域的面积S1、S2、S3、S4,以此作为四象限法解算的基础.

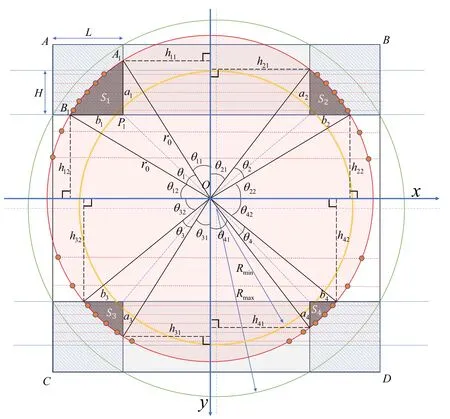
图1 太阳指向镜算法原理图.正方形ABCD为2048×2048 pixel CMOS探测器,红色圆为太阳像光斑,绿色圆和黄色圆之间为仪器允许的光斑边缘移动的区域.其中,在H(≈278 pixel)范围内选取了5行数据;其他各符号的定义见2.2节.Fig.1 Principle diagram of solar aspect system algorithm.The square AB CD is a CMOS detector with size of 2048×2048 pixels.The red circle represents the image of the solar disk with its limb limited between the green and yellow circles.And f ive rows of data are selected in the range of H(≈278 pixel).See Sec.2.2 for the def initions of more symbols.

2.1 边缘拟合法

最小二乘法(Least Square Method,LSM)是用于曲线拟合最常用的方法,拟合过程快速简便,且拟合精度相对较高.文献[17]中利用最小二乘圆拟合法对激光光斑轮廓进行拟合,从而定出了其中心坐标和半径.该方法同样可以用于指向镜成像的日面边缘拟合.设太阳像光斑的中心坐标为(x0,y0),半径为r0,则满足的圆方程为:

设(xi,yi)为从太阳像光斑边缘提取的第i个坐标点,将其代入(1)式并取残差为:

再求残差平方和函数:

根据最小二乘原理,有:

最后,解出满足(4)式的方程组,可以得到圆的中心坐标和半径参数[17]:

2.2 四象限法

此处的方法同传统四象限法不同,但由于算法本身的特征仍然称之为四象限法(Four Quadrant Method,FQM),其原理如图1所示.太阳光斑像(红色圆面)分别与CMOS探测器4个角的正方形阴影区域相交,对应的面积记为S1、S2、S3、S4,而该面积又可由红色圆的参数:圆心坐标O(x0,y0)和半径r0决定.以面积S1的计算为例,其面积等于扇形OA1B1的面积减去三角形OP1A1和OP1B1的面积,即

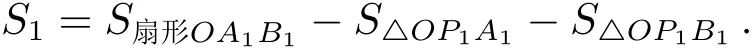
基于此,且以CMOS探测器阵列的顶点A为坐标原点,向右和向下为正方向,建立直角坐标系,则4个阴影区域的面积S1、S2、S3、S4满足

其中,带有下标的θ、h、a、b为中间参量,分别表示扇形对应的圆心角、三角形的高和底边长度.而面积S1、S2、S3、S4分别对应下面4组关系:

再将各中间参量的表达式(7)式分别代入面积S1、S2、S3、S4对应的表达式(6)式中,则可以得到以太阳中心位置(x0,y0)和半径r0为参数的方程组(8)式,即太阳的中心位置由面积S1、S2、S3、S4可以定出.

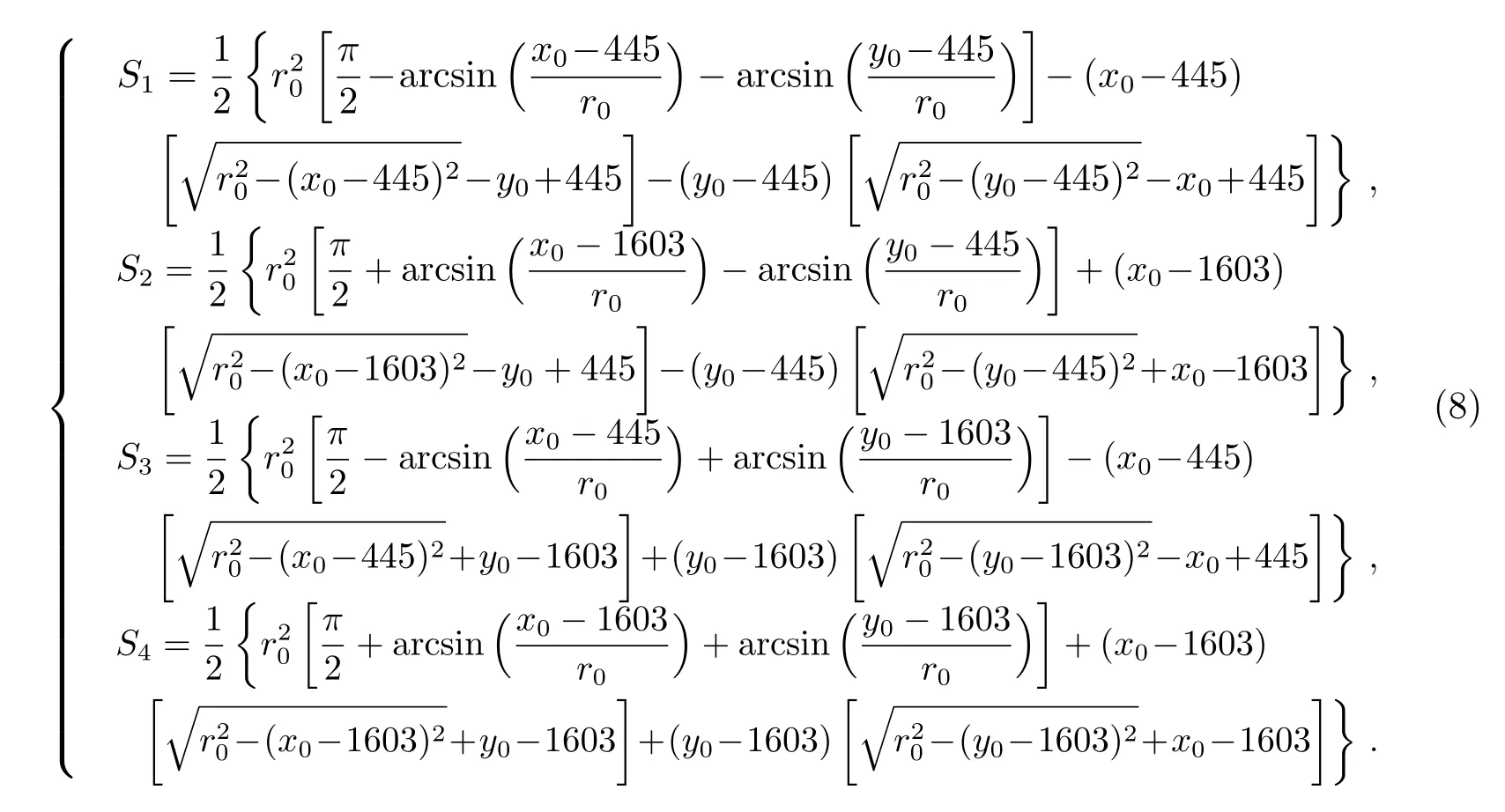
在解算时,S1、S2、S3、S4为CMOS探测器测量的已知量,由于方程组含有4个方程和3个未知数,且是含有反三角函数的复杂方程,所以考虑利用MATLAB的fsolve1fsolve,https://www.mathworks.com/help/optim/ug/fsolve.html函数进行数值求解.fsolve可用于求解非线性方程组,需要给定初值,求解时可使用边缘拟合法得到的(x0,y0,r0)作为数值求解的初值.此外,可以考虑两种做法:FQM1,将(8)式和已知的面积S1、S2、S3、S4开方后再数值求解;FQM2,考虑降低噪声的情况,将(8)式按如下方式改写构成新的方程组:(S1+S2)−(S3+S4),(S1+S3)−(S2+S4),S1−S4,S2−S3.

3 算法实现与误差评估

3.1 数据来源与测试方法

(1)由于指向镜数据来自太阳可见光,为使测试尽量接近真实情况,选择了SDO/AIA 4500˚A Level 1.0的光球数据,该数据没有作despike2despike,https://www.lmsal.com/sdodocs/doc/rep/sdod180/fid258/zip/entry/index.html处理.此外4500˚A的数据尺寸大小为4096×4096 pixel,可以使用imresize函数将其缩放到2048×2048 pixel.若在缩放前先进行裁剪,则可以控制生成的太阳像半径大小r0;

(2)为了评定指向镜算法的精度,首先直接读取f its文件为2维数组像元亮度值(Digital Number,DN),经裁剪和缩放作为第1张AIA图像(日面中心在图像中心附近),并计算其日面中心为(X0,Y0).其次对图像沿x和y方向平移(δx,δy)以产生大量测试图像,其理论中心为(XT,YT)=(X0+δx,Y0+δy).其中δx、δy从−150 pixel到150 pixel按3 pixel等间隔选取,且满足,即指向镜光轴相对于平台指向的最大偏差条件;

(3)另一方面,通过算法计算出测试图像的日面中心坐标(X,Y),再用计算得到的坐标与理论坐标相减得到x和y方向的误差(X−XT,Y−YT),则算法的误差可以表示为[6]

此外,一般认为图像是由一个个方格状的像素单元组成,方格的数量与像素的数量对应.为了反映这种认知,可以将CMOS图像的坐标原点(即A点)改为(0.5,0.5)pixel.于是对于2048×2048 pixel的CMOS探测器,其中心在(1024.5,1024.5)pixel,故在解算后需要对原中心坐标作+0.5的修正;

(4)根据太阳在CMOS探测器上成像光斑大小的可能变化,最小直径为1997.8 pixel,最大直径为2065.7 pixel,故设置了8组不同半径大小的AIA图像进行测试,r0分别约为:998、1004、1009、1014、1019、1024、1029、1035 pixel.此外考虑了图像二值化时的阈值和噪声影响,噪声是在图像二值化之后添加的.关于添加噪声,首先随机产生2048×2048的只含有0和1的二值化矩阵.其中1表示噪点,其数量与0和1总数量的比值p定义为噪声比例.然后再将噪声矩阵与二值化后的AIA图像做“或”逻辑运算,得到具有一定噪声水平p的测试图像.

3.2 测试结果与分析

为了探索随机噪声对指向镜算法精度的影响,图2中给出了四象限法的两种解法FQM1和FQM2以及LSM的误差随噪声的变化规律.其中横坐标的噪声比例在0%–1%间等间距取10个点,在2%–5%间等间距取4个点.图中每一个噪声比例下对应的蓝色*点来自821张偏移测试图像.这些测试图像从−150 pixel到150 pixel按9 pixel等间隔产生且满足指向镜光轴最大偏差条件.这些误差点总体上对误差的上限有一个限制.而紫红色的线条是测试图像在约70 pixel固定偏移下,其平均误差随噪声比例的变化曲线.这说明随着噪声的增加,FQM算法的误差呈增大趋势.此外,图3也给出了FQM和LSM的误差随噪声比例和图像偏移量的分布图.

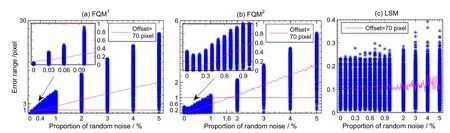
图2 不同比例随机噪声下的指向镜算法误差(阈值=1500 DN,r 0=1014 pixel).每个噪声比例下的蓝色*点来自于821张测试图像,紫红色线条是偏移约为70 pixel测试图像的平均误差曲线.(a)和(b)中的子图是满足误差小于1 pixel(红色直线以下)的局部放大图.Fig.2 The error of solar aspect system algorithm under different proportions of random noise(threshold=1500 DN,r 0=1014 pixel).The blue points*under each noise ratio are the errors of 821 test images,and the magenta curve is the average error of the test image with 70 pixel of fset.The subgraphs in(a)and(b)are the local enlarged ones satisfying the error less than 1 pixel(under the red line).

由图2可知,FQM1和FQM2满足误差小于1 pixel的噪声比例分别约为0.1%和0.85%(对于偏移量为70 pixel的图像,FQM能忍受的噪声上限分别约为0.4%和1.6%).而LSM的误差随噪声的变化相对稳定且小于0.4 pixel.此外,由图2(a)的子图可知FQM1的误差是随噪声逐渐增加的,在大约小于0.02%的噪声水平时,此方法的精度优于FQM2和LSM.而LSM对噪声的适应性以及精度总体上好于FQM,故后面的测试主要基于FQM1和LSM,当然3种计算方法可以用来相互验证.

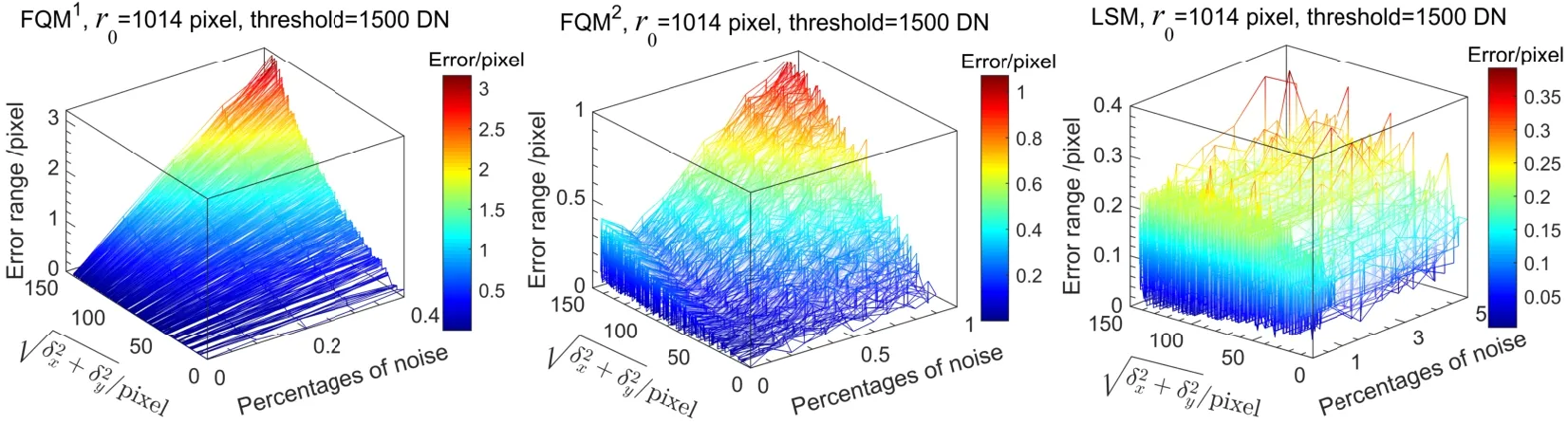
图3 FQM和LSM的误差随噪声比例和图像偏移量的分布图,对应于图2的结果.Fig.3 The error distribution of FQM and LSM with noise percentage and image of fset in Fig.2.

基于图2和图3的初步分析,接着做了更细致的测试.图4给出了对边缘拟合法和四象限法在固定阈值、随机阈值和附加随机噪声情况下的6种测试结果.其中横坐标为8组不同半径r0测试图像的统一编号,大约56000张.纵坐标为算法误差∆T的浮动范围.表1也给出了相应误差的统计结果,包括均方根(Root Mean Square,RMS)、平均值、极值以及99.5%分位值.

图4 太阳指向镜算法在不同条件下的误差分布:(a)和(b)为固定阈值1500 DN,(c)和(d)在1200−1900 DN之间随机取阈值,(e)和(f)除了随机阈值外再附加0.05%的随机噪声.Fig.4 The error distribution of solar aspect system algorithm under different conditions:(a)and(b)with fixed thresholds of 1500 DN,(c)and(d)with random thresholds of 1200−1900 DN,(e)and(f)with noise percentage of 0.05%in addition to random thresholds.

表1 太阳指向镜算法的误差评估:LSM和FQM 1Table 1 Error evaluation of solar aspect system algorithm:LSM and FQM 1

结合图4和表1可知,在固定阈值下四象限法的误差最小,误差为0.05′′以内的数据占99.5%,最大误差不超过0.06′′,优于边缘拟合法的结果.在单独考虑随机阈值以及再附加0.01%的随机噪声情况下,FQM1的各项指标依然优于LSM.当对测试图像添加0.05%的噪声时,FQM1的极值误差接近0.8′′,相对于LSM增加更为显著.添加随机噪声后的图4(f)的误差分布相对于无噪声的图4(d)变化更明显.不过根据图4(f),极值误差与太阳像的半径和偏移量有关系,故误差的评估也需要借助其他统计量,如RMS误差为0.23′′.由于四象限法的精度取决于CMOS上太阳像经二值化后4个边角的面积,可以预计随着噪声的继续增加,FQM对面积的分辨变差会导致误差增大,这也与图2(a)和(b)的结果相符.而对于LSM,比较图4(a)、(c)和(e)可知,其误差波动都比较随机均匀,再结合表1中LSM的统计结果,有无噪声相差不大;也符合图2(c)的预期.

图5选取了图4(e)和(f)中半径r0=1014 pixel的数据点,画出了LSM和FQM1的误差随图像偏移量的分布.其中横、纵坐标分别为沿x和y方向的图像偏移量,左图为边缘拟合法,其误差分布相对均匀.右图为四象限法,根据色值可知通常在太阳图像的偏移量较小的时候其误差较小.该结果也可与图2和图3的分析相互印证.

图5 太阳指向镜算法误差随图像偏移量的分布.对应图4(e)和4(f)中r 0=1014 pixel的测试数据.Fig.5 The error distribution of the solar aspect system algorithm with the image of fset and corresp onding to the test data of r 0=1014 pixel in Fig.4(e)and 4(f).

4 总结与讨论

我们针对HXI的耀斑源区定位需求以及HXI太阳镜指向精度优于2′′的设计要求,在查阅和借鉴太阳导行镜相关资料的基础上,对两种基础算法,即最小二乘法和四象限法的测量精度及其受噪点水平的影响进行了测试.测试时利用了SDO/AIA 4500˚A的Level 1.0数据.

总体而言,边缘拟合法和四象限法的精度(在0.05%噪声下RMS误差分别约为0.11′′和0.23′′)均优于2′′的设计要求和1′′的测试目标,且可提供独立测量结果,用于交叉验证.四象限法依赖于4个角的面积对太阳中心坐标的约束,所以其精度对面积的变化比较敏感.前面提到的两种解法,FQM1可以达到最高精度时的噪声容忍约为0.02%,FQM2虽然能够容忍约0.85%的噪声,但是精度总体不如LSM好.而边缘拟合法的定位精度虽然相对略低,但是由于该算法是基于拟合太阳像的边缘点数据,其所选取的14行像素相对于总的2048行像素而言,在概率上能保证具有较强的抗随机噪声能力.

但需要指出的是HXI太阳指向镜在轨提取太阳图像时,将无法对原始数据作复杂的矫正处理,故在二值化后如果还存在较多噪点,则边缘拟合法会更适合作为指向镜算法.就测试使用的SDO/AIA 4500˚A Level 1.0数据而言,四象限法的FQM1解法在低噪声时的指向精度更高.但Level 1.0数据是Level 0数据经过一定处理得到的,当前测试中,我们尚未考虑这两种数据的具体差异,所以测试会有局限性,特别是对于四象限算法.在本文所得结果的基础上,我们将进一步优化算法,如采用穷举矩阵方法以及改进四象限法方程组的求解方法等,以改进太阳中心位置的测量精度.