转子系统动力学分析软件设计

（沈阳鼓风机集团股份有限公司，辽宁沈阳 110869）

1 引言

在工业生产中，大多数设备产品都装有旋转机械，在研发设计过程中就要考虑旋转机械的各种动态问题。传递矩阵法是一种解决压缩机等重要设备机械中相关转子动力学问题的简便、高效方法。文献[1-3]利用整体传递矩阵方法，计算了各向同性支承某压缩机整机的临界转速。与传统方法相比，传递矩阵法没有多余引入方程，利于开发通用软件。

本文应用C++Builder软件和基于Riccati变换的整体传递矩阵法，以转子系统为研究对象，开发了开发出分析多转子系统动力特性的通用可视化软件，对其临界转速、固有振型、应变能分布、不平衡响应进行分析，为转子系统设计提供理论上的依据。

2 Riccati传递矩阵法

Riccati传递矩阵法，不但具有Prohl传递矩阵法的优点，还具有很高的数值稳定性，大大提高计算精度，解决振型计算中的末端幅值急剧增长的失真问题。本文针对各向同性转子的临界转速与振型应用Riccati传递矩阵递推公式进行了探索研究。

Riccati传递矩阵法[4]把状态向量中的r个元素分为{f}，{e}两组，相邻截面的状态向量之间的关系可表示为

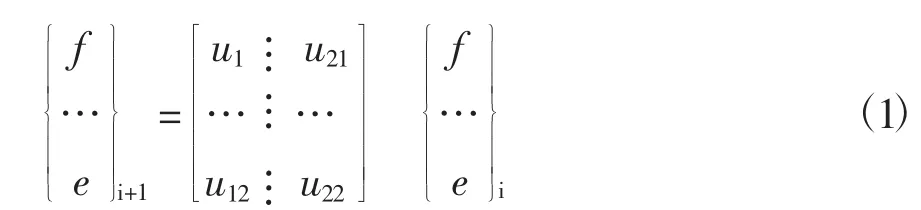
对于盘轴单元，由刚性薄圆盘弹性轴的传递矩阵可知

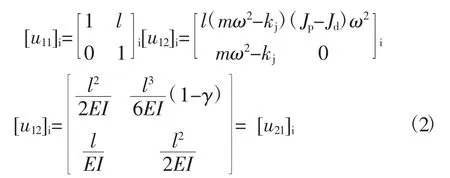
将式（1）展开可得

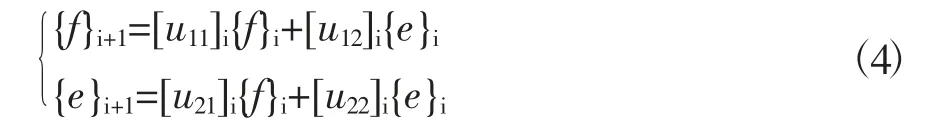
引入Riccati变换

最终可得

公式（6）就是Riccati传递矩阵递推公式，也是本文计算程序软件的基本原理和依据。

3 软件界面简介

本文开发的可视化软件，其界面友好，操作更为简单，也可根据用户指定的来存储或提取文件和图片。

软件具有选择输出类型，点位是否标识，轴段数，计算步长数等控制填写位置，方便程序计算；输出计算的临界转速和各转速下的振型；输出各阶转子激起临界转速值和临界转速点，形成临界转速特性图谱。具体输入输出数据见图1和图2。

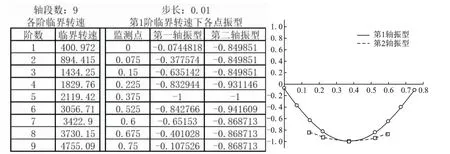
图1 临界转速和振型

图2 临界转速特性图谱

4 算例验证

4.1 单转子系统

如图3所示转子是对称的，转子简化为集总质量模型，无阻尼单转子临界转速计算结果，见表1。

图3 转子支承模型[5]

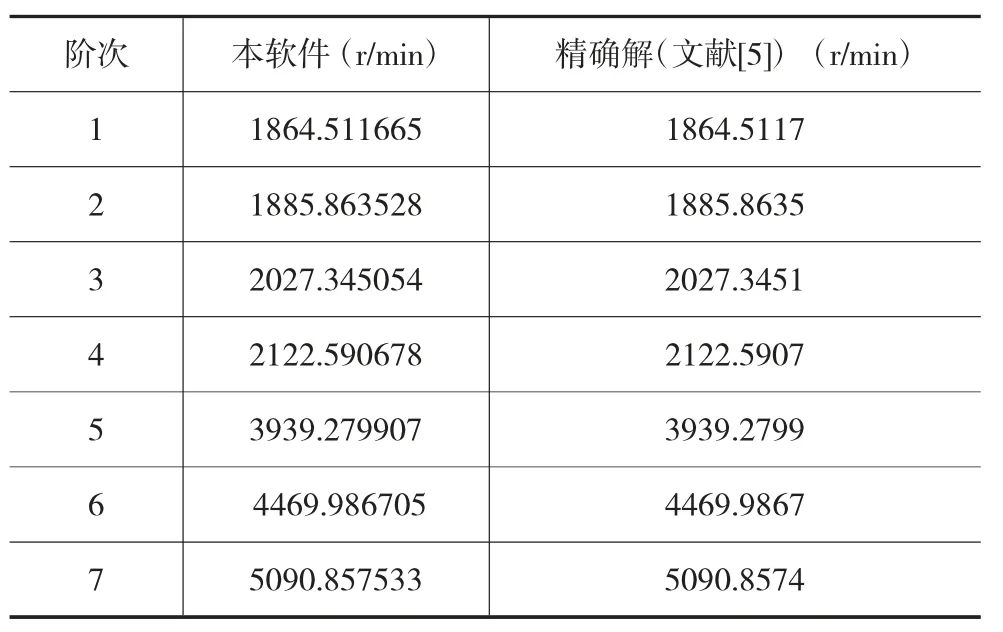
表1 转子的临界转速

图4 具有2个中介支点的无阻尼双转子轴对称系统的计算模型[6]

4.2 典型双转子系统

如图4所示具有2个中介支点的无阻尼双转子轴对称系统的计算模型。

表2是具有2个中介支点的无阻尼双转子轴对称系统固有频率的计算结果。

由表2可做误差曲线图如图5所示。

由表2和图5可以看出，利用本程序计算所得的临界转速值与利用拉格朗日方程求得的精确解[6]误差不超过0.25%，极接近精确解。从而再次证明了该算法的有效性和实用性。再此基础上做出系统的不平衡响应和应变能分布情况。如图6和图7所示。

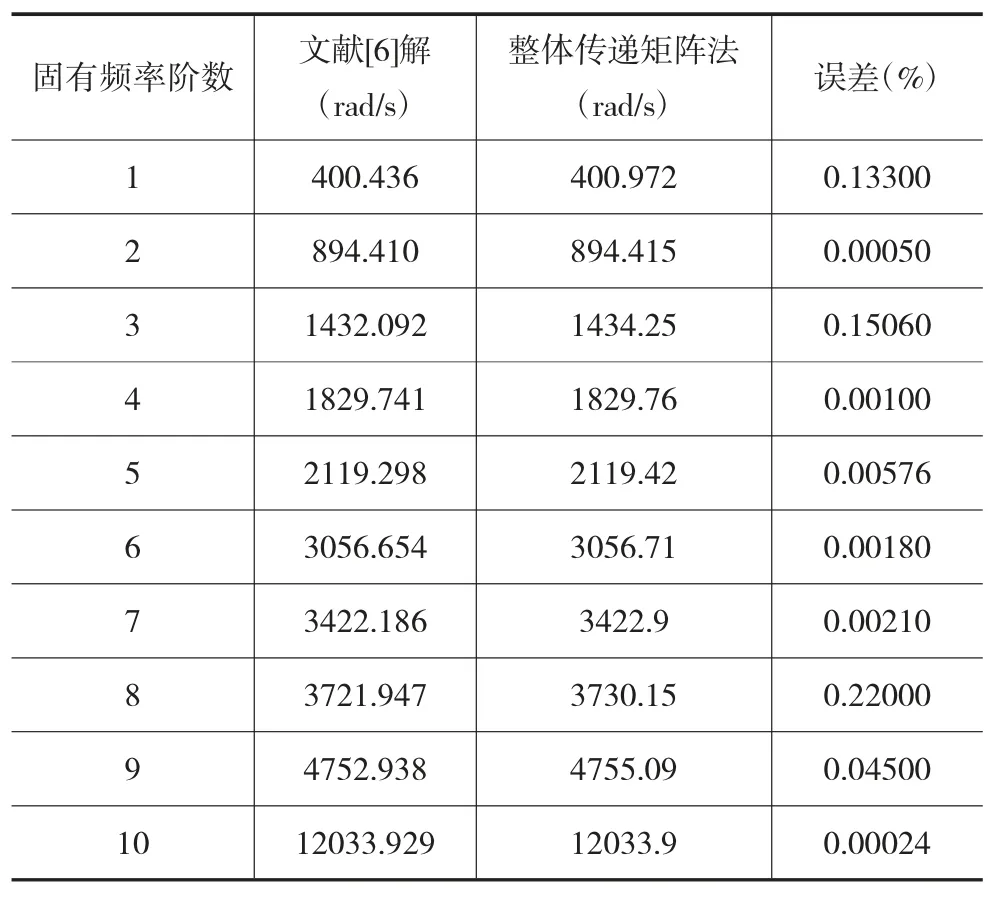
表2 具有2个中介支点的无阻尼双转子轴对称系统固有频率的计算结果

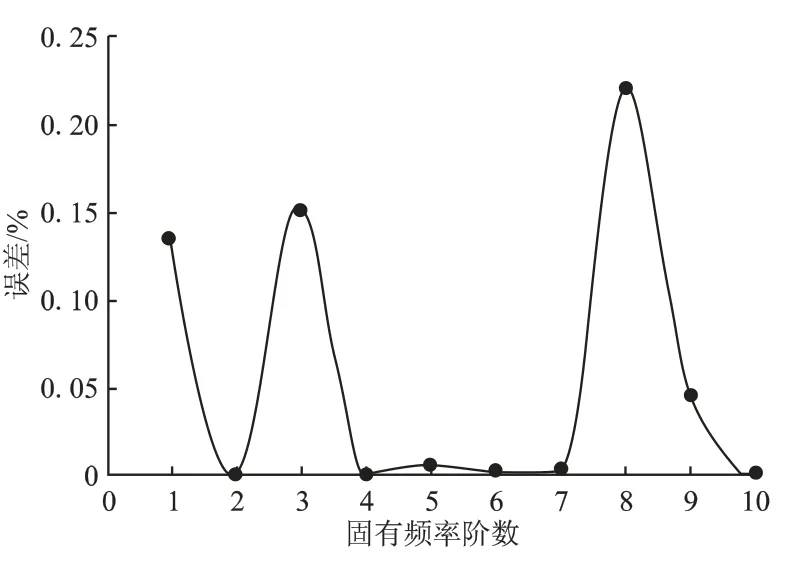
图5 误差曲线图

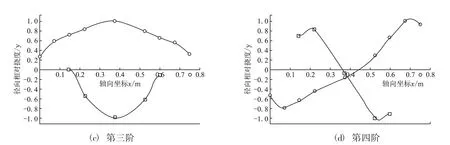
图6 振型图

图7 各阶振型时的应变能分布图

如4.1算例所示，按照上述的算法在节点4和节点10上加上较小的偏心量，可算得各个节点的频域响应图，如图9，10所示。

为了清楚地看出某个具体节点随频率变化的响应情况，本文绘制了各个节点的频响幅值谱图，如图11所示。

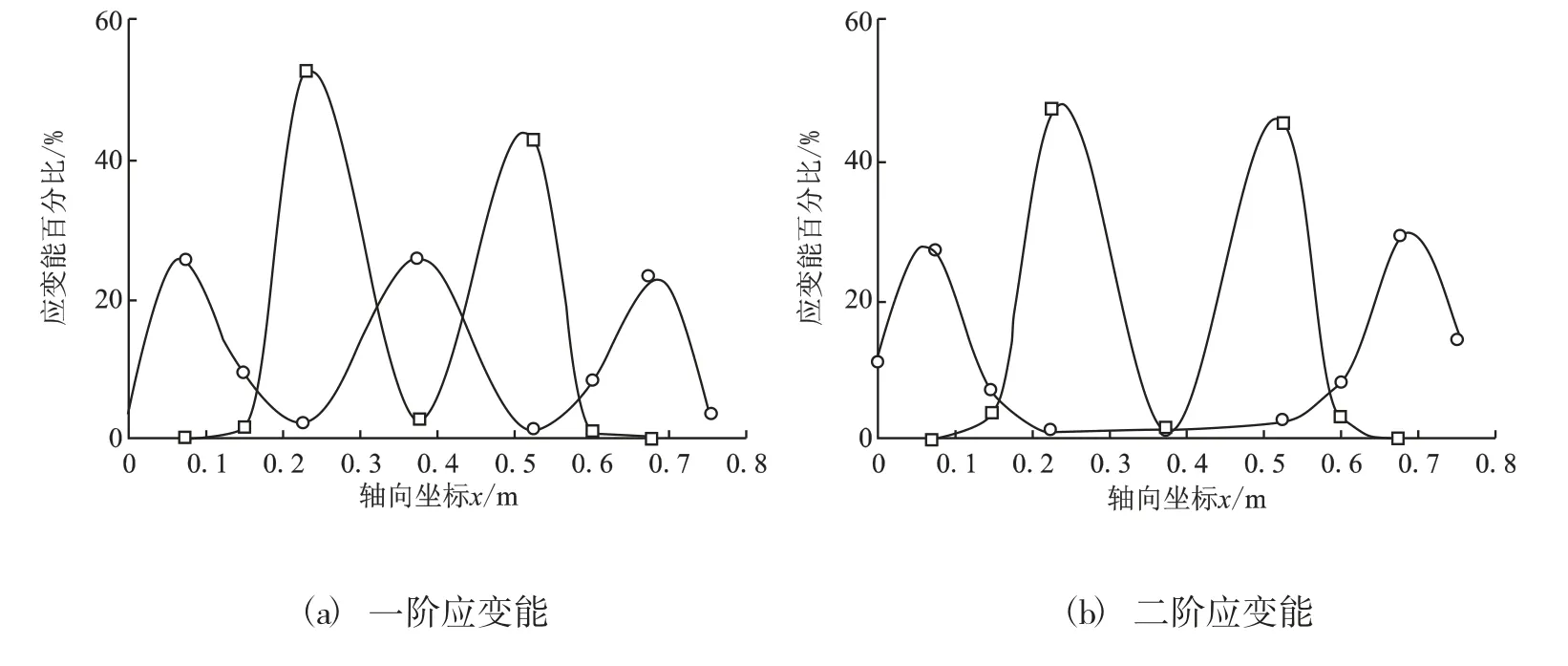
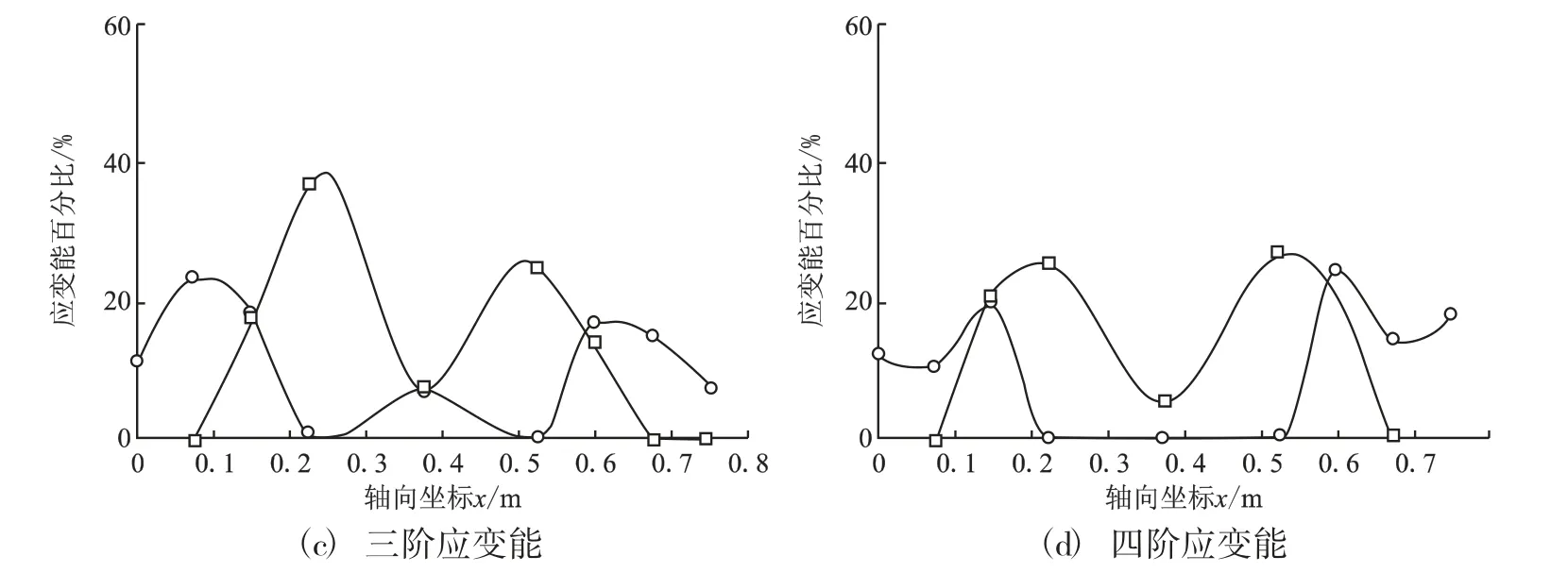
图8 各阶振型时的应变能百分比

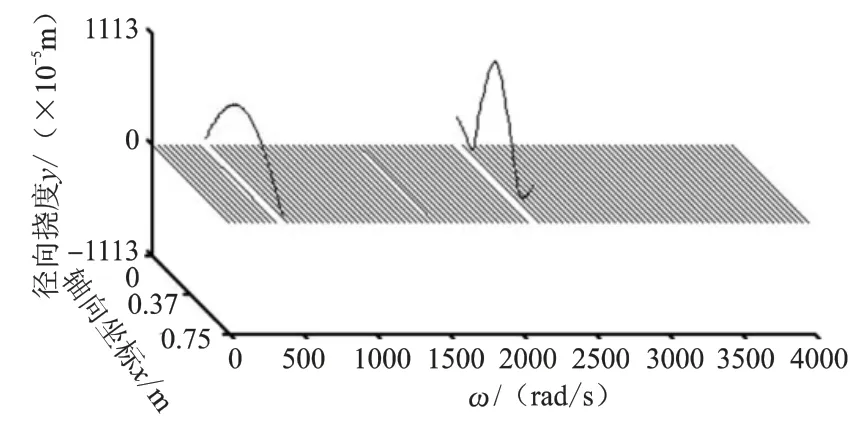
图9 内转子的不平衡响应图谱

图10 外转子的不平衡响应图谱

图11 不平衡响应图谱

4.3 具有畸形结构的双转子系统

在实际的多轴压缩机的转子中，一般结构中要具有畸形结构，本文在构建模型时，将该结构等同简化为多转子系统，即对该系统中的畸形结构看成一根轴处理，整体扩展为一个多轴转子系统。将畸形结构等价扩展成的新轴与两主体轴之间的约束关系简化为刚度较大的耦合弹簧。

图12所示的简化转子计算模型为本文涉及的某型压缩机转子系统，可以等价看成简化的弹簧连接的多根转子之间互相作用构成的一个转子系统。

本文研制的计算程序应用基于Riccati变换的整体传递矩阵法，计算得到该转子系统前八阶临界转速值如表3所示。

此处需要值得注意的是两根转子的转速是固定值。在工程实际应用中，还有一种常见情况：2根轴的转速满足w1=f（w2）的函数关系。

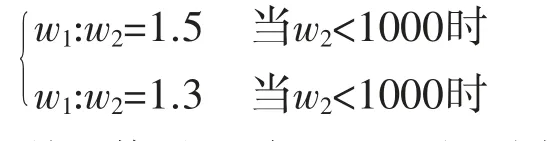
利用传递矩阵法可以得到实际压缩机内外转子引起的临界转速，同步得出该系统相关数据绘制的临界转速特性图谱，如图13所示。

得到的临界转速如表4所示。

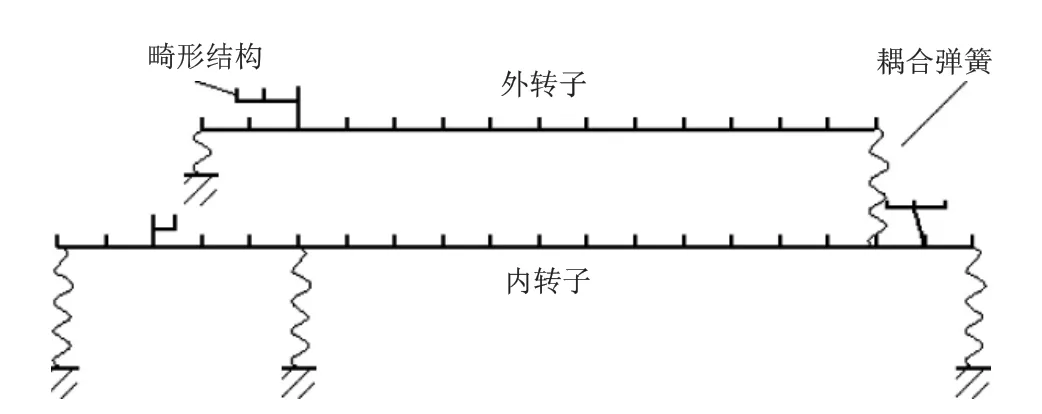
图12 转子计算模型

表3 转子的临界转速 单位：r/min

图13 某压缩机转子系统的临界转速特性图谱

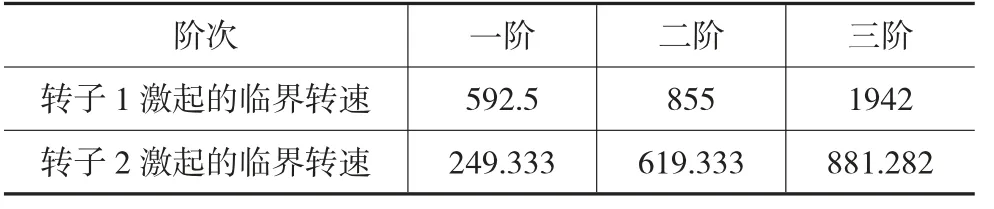
表4 某压缩机转子系统的临界转速 单位：rad/s

5 结语

（1）基于Riccati变换的整体传递矩阵法，运用编程语言编写的软件可以对复杂转子的动态特性进行计算，计算结果可靠、精确。

（2）本文开发的通用软件运行可靠，操作方便，拥有完全自主的二次接口。对复杂转子系统的快速设计与动态性能优化提供了有力的工具。