应用模型思想求线段和的最小值

王莉丹 朱宝林

(1.广西桂林市宝贤中学 541001；2.广西桂林市第三中学 541001)

模型：如图，点A、B为定点，点P是直线l上的一动点，当点P移动到P′,即A、P、B三点共线时，由公理“两点之间线段最短”知PA+PB的最小值为AB.

例1如图1，正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为____.

分析定点D、E在直线AC同侧与动点P不可能共线，通过轴对称将点D、E转化成在直线AC异侧的情形，便可用模型求解.

解∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE,当点B、P、E共线时,PD+PE的最小值为BE.

∵正方形ABCD的面积为16,∴AB=4,又∵△ABE是等边三角形,∴BE=AB=4,∴PD+PE的最小值为4.

分析由于定点A与动点M、N在运动过程中不可能共线，利用全等换线段，转化为模型中的两定点一动点的问题便可求解.

解连接DN，AD，如图，易得D(3,5),A(﹣3，0)，C(0，4)，则AC=5.

∵AC=BC，CO⊥AB，∴OC平分∠ACB，∴∠ACO=∠BCO.

∵BD∥OC，∴∠BCO=∠DBC.

∵DB=BC=AC=5，∠DBC=∠ACO，CM=BN，

∴△ACM≌△DBN，∴AM=DN,

∴AM+AN=DN+AN.

而DN+AN≥AD(当且仅当点A、N、D共线时取等号)，

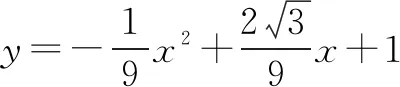
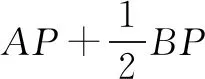
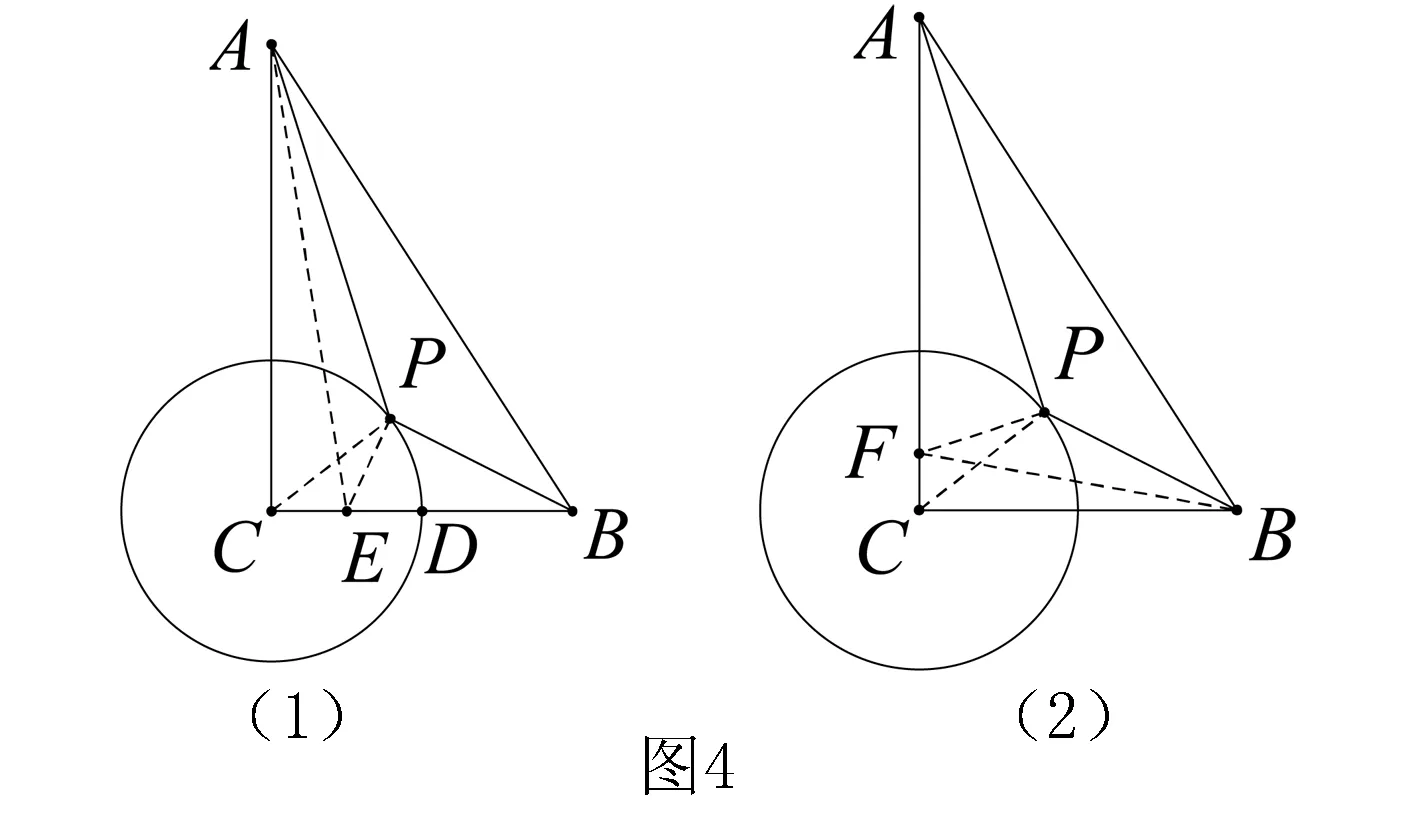
解取CD中点E，连结CP、PE、AE.

而PA+PE≥AE(当且仅当点A、P、E共线时取等号)，

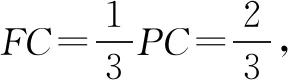
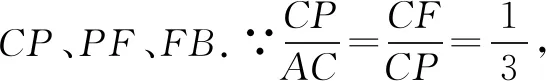
通过上述问题的探究，我们可以发现，解决此类问题通常可以采取的策略是: 把已知问题转化成容易解决的问题，即联想我们熟知的几何基本模型，化归到“两点之间的所有连线中，线段最短”的模型来解决，即想方设法把几条线段放到同一直线上，常用的换线段方法有轴对称、全等、相似等.认清了这一点，便能使复杂问题简单化，迅速找到问题的突破口.在平面几何的教学中，教师要重视几何基本模型的提炼，帮助学生在复杂图形中识别或构造基本模型,深刻领悟模型的本质特征；鼓励学生尝试从不同角度拓展模型，并在应用中彰显其魅力，从而促进学生解题经验的积累和思维水平的提升，真正提高学生的数学素养和解决问题的能力.