有限单元思想在静电场与稳恒磁场求解中的应用

仰振东，何 沛，沈 陵，王 悦，李伟艳

（铜陵学院 物理教研室，安徽 铜陵 244061）

1 问题的提出

在真空中的静电场，通过任何闭合曲面的电场强度通量，等于该曲面内所有电荷量的代数和除以ε0[1]，即：

式（1）右边为闭合曲面内电荷代数和，通常很容易获得，但式（1）左边是矢量标积的积分计算，计算过程非常复杂。仅仅在电场对称分布时，该积分计算过程可简化，如电场呈球对称分布（均匀带电球，球壳），电场轴对称分布（均匀带电导线），电场呈镜面对称性分布（无限大带电平板）。它们特定高斯面的电场强度通量有两种情形[2]。

1.空间存在一电荷量为q，半径为R的均匀带电球壳，则通过距离球心为r的球形高斯面的电场强度通量为：

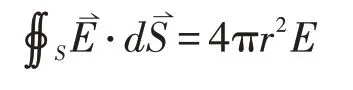
2.空间存在一单位长度所带电荷量为λ的无限长带电导线，则通过与带电导线共轴的柱高为h，底面半径为r的圆柱闭合高斯面的电场强度通量为：

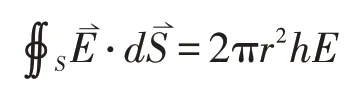
在真空中的稳恒磁场，磁感应强度B⇀沿任何闭合曲线的线积分等于真空的磁导率μ0乘以穿过以该闭合曲线为边界所张任何曲面的各恒定电流的代数和[3]:

磁场分布具有对称性特征时，式（2）左边的积分计算可以简化，如通有电流为I的无限长载流导线，在以长直导线为中心，半径为r的圆环上磁感应强度矢量的线积分可表示为[4]：

现有教材对具有对称性分布电场通过高斯面的电场强度通量以及对称性分布磁场的环路积分计算仅仅作简单的陈述，学生较难理解。对此文中通过引入有限单元思想，将闭合曲面的电场强度通量以及磁场的环路积分计算进一步深入展开，易于理解。

2 方法解析

对称性分布的电场经过某一闭合曲面的电场强度通量的求解，可以采用有限单元思想，将整个闭合曲面进行网格划分，获得N个面元dS，当N取极限时，每个面元均很小，所以面元处的电场可以近似为均匀电场，该面元可以近似为平面，所以整个闭合曲面的电场强度通量可由下式表达：

最后根据高斯面电场强度的大小方向，以及高斯面面元的大小方向，对式（3）化简计算得到结果。

同理，对称性分布的磁场沿着某一闭合曲线的积分求解，可以将整个闭合曲线进行分段划分，获得N个线元dl，当N取极限时，该线元处的磁场可以近似为均匀磁场，该线元可以近似为直线，所以整个闭合曲线的磁感应强度线积分可由下式表达：

最后根据线元上磁感应强度的大小方向，以及线元的大小方向，对式（4）化简计算得到结果。

2.1 球对称电场强度分布计算

例题1：电荷量为q半径为R的均匀带电球壳，产生的电场强度分布。

图1 球对称电场强度分布

作如图1所示的半径为r的球形高斯面，并将整个高斯面进行网格划分为N份，其中第i个面元记为，该处电场强度记为，该高斯面的电通量为：

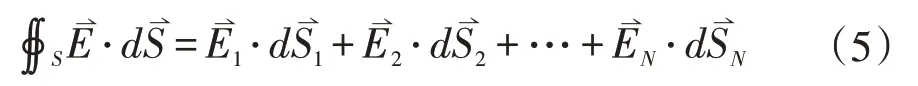
第i个面元的法线方向如图1所示，由球心沿球半径向外，与该点电场强度方向相同，可得

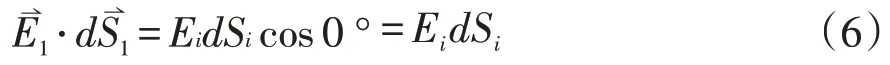
将式（6）代入式（5）得

又根据电场分布的对称性，即整个球面上的E⇀大小都相等，令其为E得

将式（8）代入式（7）得

其中dS1+dS2+…+dSN为球面的表面积。

最后根据高斯定理可得：

当r＜R时，高斯面所包围的电荷量为零，

所以E=0

当r＞R时，高斯面所包围的电荷量为q,

2.2 轴对称电场强度分布计算

例题2：单位长度所带电荷量为λ的无限长带电导线所产生的电场强度。

图2 轴对称电场强度分布

作如图2所示与带电导线共轴的柱高为h，底面半径为r的圆柱闭合高斯面，则整个闭合曲面的电通量可以写为：

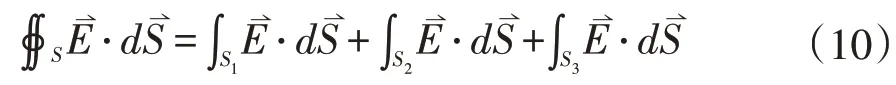
由于电场的轴对称分布，S1、S2面上任意面元的法向与该处的电场方向相互垂直，得

S3面，采用网格划分为N份，其中第i个面元记为，该处电场强度记为，则通过S3面的电通量为：

第i个面元的法向如图2所示，与该处的电场强度同向，所以

将式（13）代入式（12）得

又根据电场分布的轴对称性，即整个侧面S3上的电场强度大小都相等，令其等于E可得

将式（15）代入式（14）得

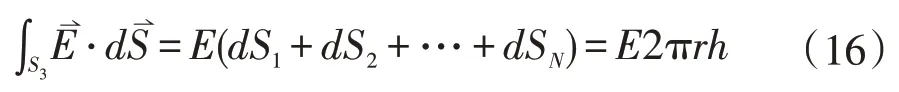
其中dS1+dS2+…+dSN为圆柱侧面表面积。

将式（11）、式（16）代入式（10）得：

最后根据高斯定理

2.3 轴对称磁场分布计算

例题3：通以电流为I的无限长直导线所激发的磁场在空间的分布。

图3 轴对称磁场分布

作如图3 所示垂直于轴线平面内以轴线为中心，半径为r的圆环。将圆环分割为N份，其中第i个弧段记为，该处记为，则通过整个圆环的线积分可表示为：

第i个弧段，弧线方向如图3所示，与该处的磁场方向相同，所以

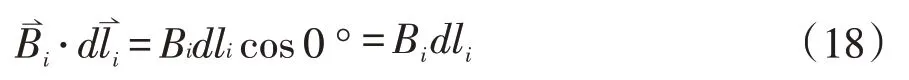
将式（18）代入式（17）得：

又根据该磁场分布的轴对称性，即整个圆环l上的磁感应强度大小均相等，令其等于B得：

将式（20）代入式（19）得：

其中dl1+dl2+…+dlN为圆环周长。

最后根据稳恒磁场的安培环路定理得：

3 结束语

本文通过引入有限元思想，对静电场高斯面的电场强度通量以稳恒磁场的环路积分作详细分析，充分体现了有限元思想在物理学中的应用，便于理解对称性分布电场以及对称性分布磁场的计算过程。