基于证据理论融合两级分类规则的不平衡数据分类方法
李莎莎
(安徽广播电视大学,安徽 合肥 230039)
1 引 言
现实世界中不平衡数据分布广泛[1],在医疗诊断、入侵检测以及文本分类等领域中多有涉及[2],正确识别少数类样本具有极其重要的现实意义。不平衡数据中类的分布是不平衡的,只通过一组具有较好分类性能的分类规则很难取得较高的分类准确率[3]。若对训练集提取两组分类规则,简单投票又可能因产生过多规则冲突导致分类准确率下降。证据理论方法[4]可将每组分类规则作为一组证据,通过将多组分类规则集成,建立基于多证据组决策模型,能够有效地融合多分类器中的分类信息,从而提高分类准确率。
文中提出的基于证据理论的不平衡数据分类方法CET(Classification based on evidential theory)是通过对原始不平衡数据集学习两次生成两组分类规则,利用证据理论融合两组分类规则。一次学习假定数据类分布均衡,通过决策树[5]分类器提取规则。二次学习用于提取更多少数类信息。首先,利用信息增益度量少数类样本与多数类样本距离,按距离将多数类样本进行排序;依次从多数类中提取与少数类样本等量的数据并与之结合,生成多个平衡小训练集;在每个小训练集上以决策树作为基分类器提取二级规则。采用证据理论方法,根据两级分类规则的分类结果计算基本概率,使用Dempster合成规则计算具有最大可信度的类别作为两组分类规则的集成分类结果。实验证明该方法在不平衡数据学习时,少数类样本以及整体数据集的分类准确率都能得到有效提升。
2 相关研究成果
2.1 不平衡数据分类方法
本文考虑两类别不平衡数据学习问题,当存在多类别数据的不平衡情形,将少数类类别通称为正类,多数类类别通称为负类。目前,不平衡数据学习方法常见策略有代价敏感学习[6]、数据采样[7]、boosting技术等。Boosting技术通过组合多个分类器迭代创建集成模型,避免分类器过拟合,如RUS-Boost[8]和 DataBoost-IM[9]等。RUSBoost 应 用 随 机 欠采样从多数类随机移除样例,克服欠采样引起信息丢失问题,但没有最大限度的挖掘少数类与多数类边界信息。
2.2 基于证据理论分类
Huawei Guo 等人在2005 年提出了基于证据理论的决策树算法[10],使用新的证据理论合成规则。2009年Yang Yi等人提出了基于证据理论的多分类器集成方法[11]。但这些分类方法未充分考虑不平衡数据分类特点。
3 基于证据理论融合两级分类规则的不平衡数据分类
3.1 两级规则生成方法
元组T={t1,t2,…,tn}中,每个元组t有m个属性{A1,A2,…,Am},C为类标 {C1,C2,…,Ck}。每个样本v代表一个属性值,规则r包含多个样本v和一个类标c,形式为v1∧v2∧ … ∧vl→c。分类规则由分类器中提取,如果一个元组t满足r中v1∧v2∧…∧vl的形式,r预测t属于类别c。
CET 选取值覆盖决策树作为基分类器:根据信息增益度量,选取能覆盖元组T的一组最优属性值v1,v2,…vi,在每个属性值vk各自条件库中递归选取最优属性值与vk连接生成pattern。当每个patternX在Ti上的信息增益等于0,X可预类别C,X→C属于一级规则。
任意两个样本X与Y相同属性值为v1,v2,…vn,X与Y的距离定义如下[12]:

由定义2知,两条样本距离越近,代表两条样本间相似程度较高。
CET 建立二级规则,首先度量每条多数类样例与少数类样例的距离,按距离将多数类样例由近至远进行排序。排序后从多数类样本中按距离选择与少数类样例相同数目的样例,与少数类样例进行混合,将原始训练集划分为多个平衡类别的小训练集。在这些平衡小训练集中,有些训练集是少数类与距离最近的多数类样本组合而成,这些小训练集组合少数类以及少数类边界样本,对预测类别有着更重要的决定作用,称为重要小训练集。因此在预测未知实例的类别时,应给与更高的权重。在每个小训练集上做值覆盖决策树算法,得到多组分类规则。在测试时,每组规则都可以为未知样例预测类别。
3.2 证据理论合成规则
CET使用证据理论将提取的规则作为两组证据构建识别框架,在测试未知实例时,将两组规则作为两个mass函数进行规则合成。
第二组规则提取通过构建多个平衡小训练集,每个平衡训练集中提取的分类规则都能对未知实例进行类别预测。将规则按照置信度conf(X)和支持度sup(X)排序[13],匹配未知实例在整体训练集上的最高conf(X)和sup(X)的规则,对未知实例进行类别预测。在得到多个预测结果之后,需根据小训练集的重要程度对预测结果进行权值的分配,重要训练集的预测结果具有更高的权值。选择半数训练集作为重要训练集,其结果预测比重增倍。所得结果归一化处理,作为第二组mass函数m2()。例如有4个平衡小训练集,选2个为重要训练集,每个训练集的预测结果比重分配如表1所示。

表1 平衡训练集预测未知实例比重分配
将表1 中比重分配所示,预测结果为正类和负类的概率归一化处理后分别是:

二级规则预测结果概率作为第二组mass 函数m2()。由这两个mass函数m1m2构成识别框架,根据Dempster合成规则将结果进行合成。
根据所求各类别的mass组合函数,可以计算预测各类别概率,确定最大概率类别为最终预测结果。
4 实验评价度量与结果分析
为验证CET算法有效性,在11个UCI不平衡数据集上进行10-折交叉测验,数据特点如表2所示。数据集Auto、Car和Lymph合并2个最少数目类别作为少数类样本,余下类作为多数类;数据集Glass 和Zoo合并3个最少数目类别作为少数类,余下类作为多数类。类别合并后各数据集类分布比例由表2所示。为综合评价不平衡数据分类器性能,本文将选用F-measure[14]度量少数类分类,选取G-mean[15]来衡量分类器对整体数据集的分类。

表2 UCI数据集特点
表3 列出了在11 个数据集上决策树方法、随机-CET 和 CET 方法的F-measure和G-mean值,最后一行列出每种方法在所有数据集上的平均结果。图1给出了3种方法的F-measure值的比较,图2 给出了3 种方法的G-mean值的比较。由表3 可知,利用证据理论集成两组规则,其中一种规则假定类分布均衡,而第二组规则采用随机欠采样方式生成多个类平衡小训练集,其F-measure和G-mean值高于单覆盖决策树。CET在二级规则度量多数类与少数类相近距离的边界样例,改善证据合成规则时mass 函数,分类不平衡数据的F-measure和G-mean值最高。
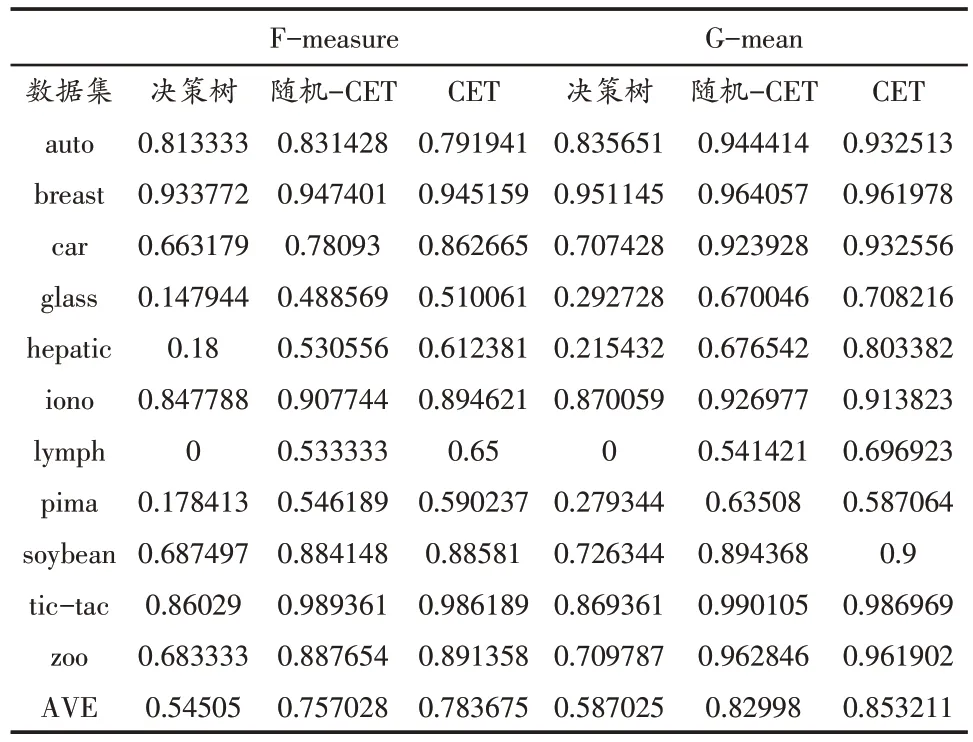
表3 3种方法的F-measure和值G-mean对比

图1 3种方法F-measure值的比较

图2 3种方法G-mean值的比较
5 总 结
不平衡数据的分类一直是分类领域中的一项难题,怎样在保证不平衡数据整体分类准确率的情况下又能正确分类少数类样例,是提高不平衡数据集分类准确率的关键。文中提出一种基于证据理论融合两级分类规则的不平衡数据分类方法,提取两级分类规则增加规则数量,且第二级分类规则根据少数类与多数类样本距离生成了多个平衡小训练集,充分考虑了不平衡数据集特点。运用证据理论将两级规则集成,解决了对少数类识别率较低的问题。实验结果表明,该算法不仅提高了不平衡数据中少数类实例的分类准确率,而且提高了数据集整体的准确率。

