高海拔汽车试验舱体结构优化研究*

张 鑫，李 屹，李家春，吴 兵

(贵州大学 机械工程学院，贵州 贵阳 550025)

0 引 言

随着我国汽车产业的发展，各类汽车环境模拟试验舱在新产品研发过程中发挥着重要作用。汽车高海拔环境模拟试验舱，简称海拔舱，主要用于为整车的高温、常温、低温及与海拔相关的试验提供所需的试验环境，是功能最全面的环境模拟试验装备[1-2]。试验舱体结构复杂，其空间结构要考虑到满足整机工作时动静态的刚强度要求，同时还要舱体结构轻量化，以降低成本。

近年来，国内外研究人员在大型舱体结构优化分析方面做了不少研究，刘晓梅[3]研究了某特种车辆工作舱体在各种不同工作情况下的响应分析，并以质量为目标函数对舱体结构进行了拓扑优化分析；史锐等[4]使用ABAQUSD对舱体在3种不同工况下强度和刚度进行有限元分析计算，得出了结构的薄弱位置；赵焕娟等[5]研究了救生舱板壳结构的优化对策，并针对不同的加筋方式进行了评价分析；千红涛等[6]提出了一种随材料内部应力大小分布不同的方案，设计了曲线加强筋板结构，其承载性能相比传统规则结构更加优越；AKI W等人[7]利用多目标优化方法研究了水下加筋壳体结构的设计，得出了加筋间距及尺寸参数最佳方案；JARMAI等人[8]研究了正交加筋壳结构在轴向受压和外压作用下的优化设计问题，利用粒子群优化算法得出了全局最小值。但针对高海拔试验舱舱体结构进行优化设计的相关研究少见报道，其普遍存在的问题是舱体质量较大，因此本文对高海拔试验舱体结构进行轻量化研究。

为此，本文对某企业正在研发的高海拔试验舱测功间舱结构进行设计，利用SolidWorks建立测功间舱体三维模型，在满足舱体结构在工作情况下的刚度和强度要求的前提下，采用多目标优化方法，通过HyperWorks/OptiStruct软件并结合有限元分析的方法，对测功间舱体进行结构拓扑优化和结构参数尺寸优化，以获得优化的舱体结构及尺寸，从而实现产品的轻量化，以期为生产实际提供理论依据和参考。

1 试验舱体结构设计

1.1 试验舱体工作情况分析

高海拔环境模拟试验舱需模拟高温、低温和高海拔低气压等环境条件，舱体在工作过程中主要经历3种工况：静力学工况、动力学工况及空间热力学工况。

静力学工况主要是指舱体在承受载荷为模拟海拔6 000 m(绝压47.21 kPa)时舱体内外的压差，内侧气压为47.21 kPa，外侧为一个大气压(101.3 kPa)，将内外压差转换为作用在舱体表面的压力，计算舱体强度时以55 kPa均布压力形式加载到舱体表面。

动力学工况主要是指舱体在工作过程中，在内、外压差变化时舱体所受到的冲击，受自身结构及外部激励影响，其结构可能会产生振动，当外部激励的频率与舱体结构某阶固有频率接近时，易产生共振现象，使舱体结构发生破坏。为保证舱体的动态性能，应提高其结构的低阶固有频率。

空间热力学工况主要是舱体内部温度变化对结构性能的影响，舱体内部利用聚氨酯绝热层做内保温处理，舱体外部为环境温度，当其工作环境温度发生变化时，舱体钢板所承受温度变化在允许范围内，基本处于恒温状态。因此，本研究中不考虑热力学工况。

1.2 试验舱体结构设计及三维建模

根据工况分析，舱体工作过程中所承受的载荷较大，尤其是在模拟高海拔环境时，整个舱体将承受负压作用，对舱体的刚度和强度要求很高。根据设计要求，试验舱体内部有效尺寸为30 342 mm× 5 000 mm×5 000 mm，结构为薄壁结构，测功间为试验舱体的中间舱段，内部有效尺寸为15 000 mm×5 000 mm×5 000 mm，舱体为空间大跨度结构，在承受负压工况下，易发生较大扰度变形，属于容易发生失效的舱段。为提高有效容积，设计时采用方形舱体，由于壳体主要承受负压作用，设计时壳体上加环向加强筋和纵向加强筋来提高承载能力。

测功间舱体结构尺寸较大，可考虑设计为一体式和分体式两种结构形式。一体式测功间舱体整个为一整体，具有较好的强度；分体式结构舱体则设计为由多个舱节通过法兰联接，法兰通过螺栓联接，一般联接处易出现应力集中，其强度比一体式差。

通过简化模型的静力学分析，如图1所示。

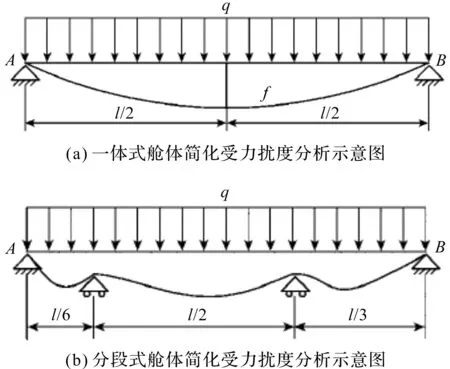
图1 舱体受力示意图

图1中，分别将壳体简化为均布载荷下两端固定的简支梁和整个舱段简化为中间加简支约束的简支梁，分析其壳体的扰度。一体式测功间舱体中，长度方向较宽度和高度方向尺寸过大，使中间扰度较大，在载荷作用下可能产生较大位移，容易不满足刚度要求；而采用分段式舱体结构时，由于单个舱段的长度相较于整个测功间舱尺寸较小，其抗弯刚度分段变化，扰度较小。

考虑到测功间舱体变形较小的要求，而强度问题一般晚于刚度问题发生的情况，故设计中笔者采用分体式的舱体结构。

单个舱段尺寸为3 000 mm×5 000 mm×5 000 mm。为便于分析与计算，笔者对舱体三维模型的局部进行简化处理。在壳体外部焊接惯性矩足够的加强筋，为避免结构的失效，初步设计时，壳体蒙皮采用18 mm厚钢板，法兰断面尺寸为30 mm×300 mm,为提高承载能力，每段舱节设有3排20 mm×200 mm环向加强筋，侧面、顶面和底面各有8排20 mm×200 mm纵向加强筋，整个测功间舱体采用5段单节舱体通过联接组成。

测功间三维模型如图2所示。

图2 测功间三维模型

1.3 试验舱体材料

舱体的设计温度为-50 ℃～70 ℃，要求材料具有较高的抗低温性能，且设计压力为内外压差0～55 kPa,材料需要具有较好的力学性能。考虑到舱体做内保温处理，舱体钢板的实际使用温度远远高于-50 ℃，从制作工艺性和性价比方面考虑，钢板材料采用低温压力容器钢16MnDR。

其材料特性参数如表1所示。

表1 材料特性参数

2 单节舱段多目标拓扑结构优化

2.1 单节舱段结构拓扑优化建模

在模拟海拔6 000 m工况下，设计首先要保证单节舱段在低压环境下满足强度和刚度的要求，由于二者中刚度一般较强度更易出现问题，将舱体刚度最大作为拓扑优化的一个目标函数，强度问题则通过约束舱体的最大等效应力条件考虑。因为结构的刚度与柔度互为反比关系，研究中结构目标刚度最大化，即转化为柔度最小化进行求解。但对于多目标优化问题，使用线性加权法存在弊端，往往不能求出所有最优解。

为提高求解优化问题的准确度，本文采用折衷规划法[9]建立静态工况下单节舱体柔度最小的目标函数为：

(1)

式中：m—载荷工况数；wk—第k个工况的权值；q—惩罚因子，q≥2；ck(ρ)—第k个工况结构的柔度目标函数；ckmax,ckmin—第k个工况总柔度的最大值和最小值；ρ—单元密度值。

在单舱体静态工况柔度拓扑优化中，考虑到舱体结构两侧面和顶面所受的压力载荷大小可能存在差异。对舱体考虑3种工况：(1)顶面受55 kPa压力载荷，两侧面受30 kPa压力载荷；(2)顶面受30 kPa压力载荷，两侧面受55 kPa压力载荷；(3)顶面和两侧面同时受到55 kPa压力载荷。同时将3种工况视为同等重要，各个工况权值大小wk取相等。

考虑舱体的动力学工况，为了保证测功间舱体结构的低阶固有频率远离共振频率，本研究以单节舱体低阶固有频率最大化作为拓扑优化的另一个目标函数。优化中常常出现这样的情况：优化了某阶固有频率，该阶频率得到了提高，但同时其他阶固有频率却出现下降，相邻的低阶频率之间发生调换，使目标函数出现频率振荡现象。因此，对低阶固有频率进行优化时，不能单独考虑是某一阶频率最优化，需要综合考虑多阶频率[10]。

本文采用平均频率公式来定义低阶固有频率拓扑优化的目标函数：

(2)

式中：Λ(ρ)—平均频率；λi—第i阶特征频率；λ0，s—给定参数，用于调整目标函数；wi—第i阶特征频率权重，此处取wi=1/6；f—需要优化的低阶频率的阶数，此处取f=6。

同时，考虑测功间舱静态多刚度目标和动态振动频率目标的拓扑优化。综合单节舱段在受压工况下刚度最大化和低阶固有频率最大，根据折衷规划法结合平均频率公式，可得到单节舱段多目标拓扑优化的综合目标函数为：

(3)

式中：ω—柔度目标函数的权重；Λmax，Λmin—频率目标函数的最大值和最小值。

考虑到刚度和低阶固有频率两个指标的相对重要性，将柔度的权值设为0.6，平均频率的权值设为0.4。

由于各个舱段的相似性，为计算简便，笔者选择单节舱段作为拓扑优化模型。本研究将单节舱体的壳体与加强筋视为整体，用壳体单元划分，将舱体的底面设为非设计区域，舱体的侧面和顶部为设计区域。拓扑优化设计变量为单元的相对密度，约束条件为体积分数上限0.4，设计区域变形小于2.5 mm，为保证强度要求，设计区域最大等效应力小于材料的许用应力180 MP。

配挖掘机1台，推土机1台，装载机1台，载重汽车3台，各种HDPE管道焊机2套，30 kW发电机2台，蛙式打夯机2台，交通运输皮卡车1台。各种机械设备状况完好，专人操作。

2.2 舱体结构拓扑优化结果与讨论

舱体结构拓扑优化采用HyperWorks中的OptiStruct模块进行计算，需要利用OptiStruct中提供的自定义函数来定义本文提出的折衷规划公式和平均频率公式，将定义好的函数设为响应，把该响应作为目标函数进行拓扑优化。

随着迭代次数的变化，从OptiStruct得出静态工况下柔度迭代历程如图3所示。

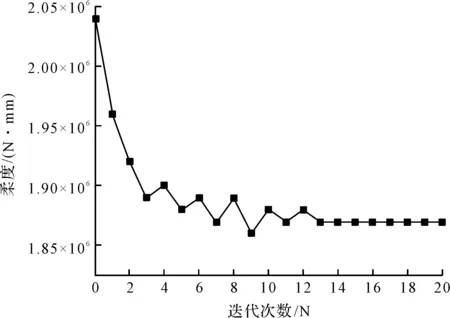
图3 柔度迭代历程

从图3可以看出：柔度开始迭代时下降较快，中间出现波动，最后达到收敛。在迭代过程中静态工况下，舱体柔度从2.04×106下降到1.87×106，减少了11.2%，提高了结构的刚度。

经过OptiStruct20次迭代计算，在满足设计约束的条件下，前三阶固有频率优化迭代历程如图4所示。

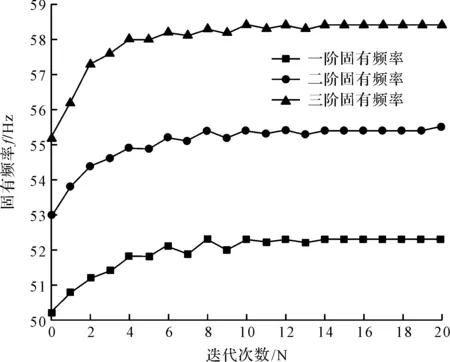
图4 频率迭代历程

从图4可以看出：频率在迭代次数进行到10次时达到收敛。前三阶频率在迭代过程中都有不同程度的提高，一阶固有频率从50.2 Hz增加到52.3 Hz，增长了4.2%；二阶固有频率从53 Hz增加到55.5 Hz，增长了4.7%；三阶固有频率从55.2 Hz增加到58.4Hz，增长了5.8%；而且在优化进程中没有发生频率交替导致的振荡现象。

经过迭代，在满足设计约束条件下，最终得到单节舱段拓扑优化密度图如图5所示。

图5 单个舱段拓扑优化结果密度图

图5的优化结果中，单元密度能够较好地趋于0或1。趋近于1区域表示单元密度高，需要保留和加强的区域；趋近于0区域表示密度较低的单元，可以根据设计减少或去除的区域。

参考拓扑优化的结果，本研究对单舱加筋结构进行重新布局，由原结构3排环向加强筋变为4排环向加强筋，侧面和顶面纵向加强筋由原来的8排变为6排，并且在中心处为减少变形，在中心处增加额外筋保证满足条件。

2.3 舱体结构拓扑优化前后性能分析

本研究将新设计的单节舱段结构组装，对整个测功间舱段进行结构性能仿真。考虑模型实际尺寸较大，为了简化计算，将舱体蒙皮、加强筋采用薄壳单元划分网格；法兰采用实体单元划分网格，螺栓联接采用刚性连接进行模拟，设置壳体单元尺寸50 mm，实体单元尺寸为20 mm；壳体底部固定，简化为沿测功间舱纵向多点固定约束，对舱体的侧面及顶面加载55 kPa的压力载荷。

图6 舱体拓扑优化前后典型云图

从图6可以看出：舱体变形主要集中在各个舱段的中间位置，拓扑优化后的变形更分散一些，减少了中间位置的变形量；最大变形从原结构的2.859 mm降低为2.205 mm，最大变形量满足小于2.5 mm的要求；舱体应力集中在顶部中间位置和拐角处的加强筋上，最大等效应力从原结构的102.4 MPa增大到117.3 MPa，但依然小于舱体结构的许用应力180 MPa，整个舱体满足强度要求。

相比原结构拓扑优化后质量从75.066 t减少到74.460 t,降低了0.8%。舱体质量优化结果并不理想，因此需要对舱体尺寸参数进行优化。

3 舱体结构尺寸参数优化

3.1 尺寸参数优化模型

为了进一步减轻舱体的质量，笔者以舱体的拓扑构型作为尺寸优化的几何模型，利用多目标尺寸优化方法对舱段壳体厚度及加强筋尺寸进行详细设计，得到舱体最优的轻量化尺寸。

优化设计变量定义如图7所示。

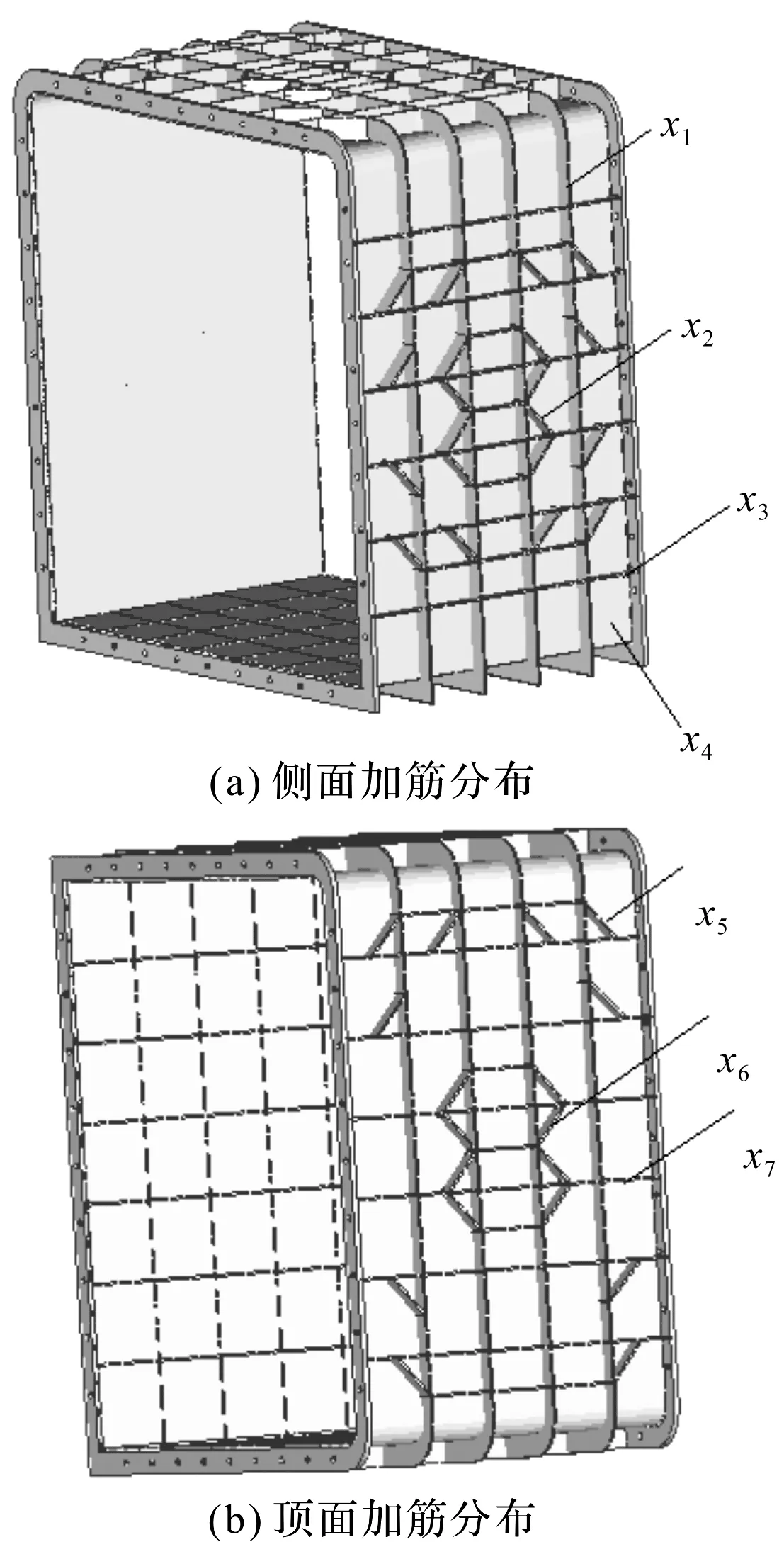
图7 单节舱体加强筋分布和尺寸定义x1—环筋的厚度；x2—侧面斜筋的厚度；x3—侧面纵筋的厚度；x4—舱体蒙皮的厚度；x5—顶面两侧边筋的厚度；x6—顶面中心斜筋的厚度；x7—顶面纵筋的厚度

优化目标为舱体的质量最小和最小变形量，在寻求目标函数最优的过程中，还需要保证舱体的工作性能满足要求，即约束条件最大等效应力小于σs=180 MPa、固有频率大于fmin=50 Hz，同时对设计变量加上下限进行约束。

由此得多目标尺寸优化的数学模型为：

(4)

式中：f1(x)—舱体质量；f2(x)—舱体的变形量；wi—第i项子目标函数的加权因子；xj—设计变量；σ—最大等效应力；f—固有频率。

根据上文的拓扑优化结果，笔者将加强筋的位置、数目及高度设为定值，利用HyperWorks中面抽取功能提取舱体拓扑构型的中面，并将舱体加强筋及蒙皮赋予属性，分别将其设置为设计变量。然后在求解器模块OptiStruct通过函数输入功能定义该尺寸参数优化问题的目标函数，并添加约束条件及目标函数的响应输出，最后求解器利用局部逼近的方法求解该尺寸参数优化问题。

3.2 参数优化结果与讨论

通过定义加强筋及蒙皮的厚度xi(i=1,2,3,…7)为设计变量，各设计变量的初始值和取值范围及最终求解得到的最优值如表2所示。

表2 各尺寸变量取值范围及优化值

本研究根据尺寸优化得到的最优值对舱体的加强筋及蒙皮厚度进行修改，对整个测功间舱段进行有限元分析验证。

优化前后结构性能对比如表3所示。

表3 优化前后性能对比

从表3中可以看出，在经过拓扑和尺寸优化后，相比原结构，测功间舱体最大变形位移从优化前的2.859 mm变化到2.470 mm，减少了22%；一阶固有频率从优化前的50.2 Hz变化到54.1 Hz，增长了7.8%，二阶固有频率从53 Hz变化到56.8 Hz，增长了7.2%，三阶固有频率从55.2 Hz变化到58.6 Hz，增长了6.2%；最大等效应力从优化前的102 MPa变化到127.0 MPa，增大了24%；质量从优化前的75.066 t变化到66.917 t，减少了10.9%。

4 结束语

(1)根据测功间舱段工作情况及设计要求，本研究对测功间舱体结构进行了分段式纵横加筋结构设计，利用折衷规划法和平均频率的思想对结构进行了拓扑优化求解，结果显示舱体的薄弱环节为壳体的中间位置及加强筋中间位置和拐角处，设计根据优化结果对加筋位置进行了重新合理布置，分析显示了各项性能指标均满足设计要求，但轻量化指标提升不明显；

(2)为进一步调整舱体结构参数以减轻结构质量，本研究以质量和变形量最小化为目标，对结构的尺寸参数进行了寻优，得出了最佳尺寸参数。结果显示，优化后质量相比原结构减少10.9%，实现了舱体结构的轻量化。

目前，该研究成果已应用于实际生产中。同时，它也可为其他的同类产品结构轻量化提供参考。