融合Canny算子和形态学的齿轮图像边缘检测研究*

陈 顺，李登峰

(武汉纺织大学 数学与计算机学院，湖北 武汉 430200)

0 引 言

图像的边缘检测是图像分割、目标识别和区域提取等图像分析领域十分重要的基础[1]。图像边缘检测的原理是提取目标与目标、目标与背景之间的边界信息[2]，关键在于有效抑制噪声，同时能检测到更多的图像边缘信息。由于图像噪声和边缘都属于高频信号，导致传统边缘检测算子对噪声敏感，难以区分边缘和噪声，不利于实际应用。现代边缘检测算法中，神经网络算法[3]、启发式算法[4]等算法搜索能力强、定位精度高，适用于各类复杂图像。但是其算法实现成本高，需要大量的训练样本建立模型，效率较低。

Canny算子是一种满足最有准则的边缘检测算子，其检测结果包含了图像更多边缘信息，所以相比其他传统算子能够取得更好的检测效果[5]。并且Canny算子从理论上首次形成了完善的边缘检测评价标准，成为评价其他边缘检测方法的标准[6]，因此，引起了许多研究者对传统Canny算子进行改进。文献[7]用自适应滤波器代替高斯滤波器进行了预处理，并结合贝叶斯判断理论，通过最大化将像素点判决到不同区域的后验概率来获取最优的高低阈值；文献[8]提出了一种基于改进Canny算子的路面裂缝检测技术，利用形态学滤波对原有的滤波方式进行了改进，使用Otsu算法实现双阈值自适应获取；文献[9]利用分治法思想和相邻窗口排序信息相关性原理来改进了自适应中值滤波器，并用二分查找原理改进了Otsu算法计算梯度幅值的高、低阈值。

数学形态学是利用具有不同形状大小的结构元素对二维图像进行数学形态学运算，最后与原图像相减来获得边缘图像，是一种分析和处理各类图像的重要方法[10]。其中结构元素的选取对图像边缘检测具有很大影响。小尺寸的结构元素虽然能很好地保护边缘细节，但去噪能力较弱。大尺寸的结构元素去噪能力较强，但去噪后的图像变得模糊，导致部分细节信息不突出。文献[11]提出了基于形态学算子和小波变换融合的边缘检测算法，采用自适应多形状的结构元素，设计了0°、45°、90°、135°方向的3×3线性结构元素和方形结构元素。该算法能有效地提取复杂背景缺陷轮廓；文献[12]提出了用差影法融合双阈值小波和数学形态学的边缘检测算法，利用多尺度多结构数学形态学算法处理低频分量。该算法具有很好的抑制噪声能力。

本文将结合改进的Canny算子和新型多尺度多结构数学形态学边缘检测的优点，对边缘图像小波分解后的子图进行自适应加权融合，得到新的边缘图像子图，重构得到最终的边缘检测图像。

1 Canny边缘检测算法分析与改进

1.1 传统Canny算子

传统边缘检测算子中，Canny算子3个基本评价标准[13]为：

(1)低错误率。所有边缘都应该被找到，检测到的边缘尽可能是真实边缘；

(2)边缘定位精度。定位边缘尽可能接近真实边缘；

(3)单一边缘响应。对于图像真实边缘，检测器应该只返回一个边缘点。

传统Canny算子边缘检测步骤如下：

(1)使用高斯滤波器对图像进行预处理，其中高斯函数方差人为设定；

(2)对预处理后的图像采用2×2模板计算梯度幅值和梯度方向；

(3)对梯度图像进行非极大值抑制，将梯度最大值点作为候选边缘点；

(4)人为确定高、低阈值并采用连接方法确定图像最终边缘。

从上述标准可以看出，传统Canny算子的高斯滤波器参数人为设定，导致滤波效果不佳；使用2×2模板计算梯度使得对噪声敏感，容易漏检真实边缘；高低阈值人为选取，自适应能力差，易产生伪边缘。因此，本文针对以上问题对Canny算子进行改进，以取得良好的去噪效果。

1.2 改进的Canny算子

1.2.1 混合滤波器

中值滤波是一种非线性数字滤波器技术，在处理脉冲噪声和椒盐噪声时效果良好，常用于图像的去噪处理。但是传统中值滤波器在保护图像细节和去噪方面存在着一定的矛盾，所以本文采用自适应中值滤波器。相比于传统中值滤波器，其具有良好去噪效果，同时能保护图像细节。

均值滤波器是一种线性滤波器，使用起来简单快速。本文选取修正的阿尔法均值滤波器。相比其他几种滤波器，修正的阿尔法滤波器去噪效果更好。

最后将采用自适应中值滤波器处理后的图像作为修正的阿尔法均值滤波器的输入，组成一个混合滤波器进行图像预处理，达到了良好的去噪效果。

1.2.2 梯度幅值和幅角

本文将原来的2×2模板改为3×3模板，借鉴Sobel算子在水平方向和垂直方向的模板，并增加45°和135°方向梯度模板。因此可以得到当前梯度幅值和梯度幅角分别为：

F(i,j)=sqrt(Fx(i,j)2+Fy(i,j)2+
F45°(i,j)2+F135°(i,j)2)

(1)

(2)

式中：Fx(i,j)，Fy(i,j)，F45°(i,j)，F135°(i,j)—4个方向的梯度幅值。

1.2.3 自适应双阈值选取

图像标准差反映了图像灰度值与均值之间的离散程度。本文根据下式所得梯度图像求出梯度均值和梯度标准差求解阈值:

(3)

(4)

H=M+σ2*σ2

(5)

式中：M—梯度图像均值；σ2—梯度图像方差；H—高阈值。

为了减少计算量，本文选取高阈值的40%作为低阈值。

2 数学形态学边缘检测

2.1 数学形态学基本运算

数学形态学建立在集合论基础上，其从集合论的角度分析、刻画图像的性质和特征，是图像处理中广泛应用的新技术之一。其基本思想是利用结构元素对图像进行相关形态学运算，从而达到对图像分析和识别的目的[14]。灰度数学形态学的基本运算有灰度膨胀、灰度腐蚀、灰度开运算和灰度闭运算。

灰度膨胀运算：

(img⊕s)(x,y)=max{img(x-i,y-j)+s(i,j)
|(x-i),(y-j)∈Di;(i,j)∈Ds}

(6)

灰度腐蚀运算：

(imgΘs)(x,y)=max{img(x+i,y+j)-s(i,j)
|(x+i),(y+j)∈Di;(i,j)∈Ds}

(7)

灰度开运算：

(8)

灰度闭运算：

img*s=(img⊕s)Θs

(9)

上述基本的灰度数学形态学算子操作起来简单快速，但是去噪效果不佳，在实际应用中难以运用。因此有学者构造出抗噪腐蚀型算子、抗噪膨胀型算子以及抗噪膨胀腐蚀型算子。

3种算子设计如下[15]：

抗噪膨胀型算子：

(10)

抗噪腐蚀型算子：

(11)

抗噪膨胀腐蚀型算子：

(12)

2.2 改进的灰度数学形态学边缘检测算法

针对以上分析，为了有效抑制噪声的同时能检测到更多的边缘信息，同时相比其他形态学算法计算复杂度更小，本文采用多尺度多结构元素灰度形态学边缘检测算子进行图像的边缘检测，设计2×2的正方形结构元素、3×3的十字形两个结构元素。

结构元素如下所示:

经过多次实验分析，改进的形态学算子如下：

(13)

式中：Ai，Bi—结构元素，Bi=B⊕B⊕…⊕B，即A和B可以经过i次结构元素的自我膨胀得到大尺度结构元素。

具体计算步骤如下：

(1)通过膨胀运算得到结构元素A1、A2和B1、B2；

(2)根据公式(13)分别求出结构元素所对应的图像边缘E1、E2；

(3)将图像边缘根据图像信息熵加权融合，最后得到的图像边缘如下：

(14)

图像信息熵反映了图像信息的丰富程度，具体公式如下：

(15)

式中：αi—各边缘图像的信息熵。

3 融合改进的Canny算子和新型数学形态学边缘检测算法

当噪声浓度较低时，改进的Canny算子具有不错的去噪效果，并且边缘定位精度高、边缘连续清晰，但是高浓度噪声下难以达到明显的去噪效果。当噪声浓度较高时，数学形态学依然具有良好的去噪效果，但是边缘定位精度低、轮廓不明显、边缘较粗。因此本文融合算法结合两种算法，根据图像信息熵自适应融合，提高算法计算效率，并且得到的边缘轮廓清晰，去噪效果良好。

为了得到效果更好的边缘图像，本文融合算法具体步骤如下：

(1)对含噪图像进行改进的Canny算子边缘检测，得到边缘图像F1；

(2)对含噪图像进行新型数学形态学边缘检测，得到边缘图像F2。为了减少计算量，令公式(13)中的i=2；

(3)由于噪声信号存在于图像高频区域，利用小波分解的优势，将边缘图像分解为低频细节子图和高频子图。为了减少计算复杂度，对边缘图像F1进行二维单尺度小波分解一层。其中小波基选用db2；

(4)对两幅边缘图像分解得到的子图像根据信息熵自适应加权融合，得到融合后的4幅子图像。融合公式如下：

F(i,j)=α1*F1(i,j)+α2*F2(i,j)

(16)

式中：α1，α2—公式(15)所求子图的信息熵。

(5)最后对子图像进行小波逆变换，得到最终的边缘检测图像。

4 实验及结果分析

为了验证本文融合算法去噪能力和边缘检测效果，实验在Matlab R2016b平台上实现，以512×512的标准Lena图像、不同大小和背景的齿轮图像为例，对比分析算法在去噪能力、定位精度、边缘连续性等方面的效果。

加入3%的椒盐噪声检测Lean图像结果如图1所示。

图1 实验1

加入3%的椒盐噪声检测Lean图像客观评价指标如表1所示。

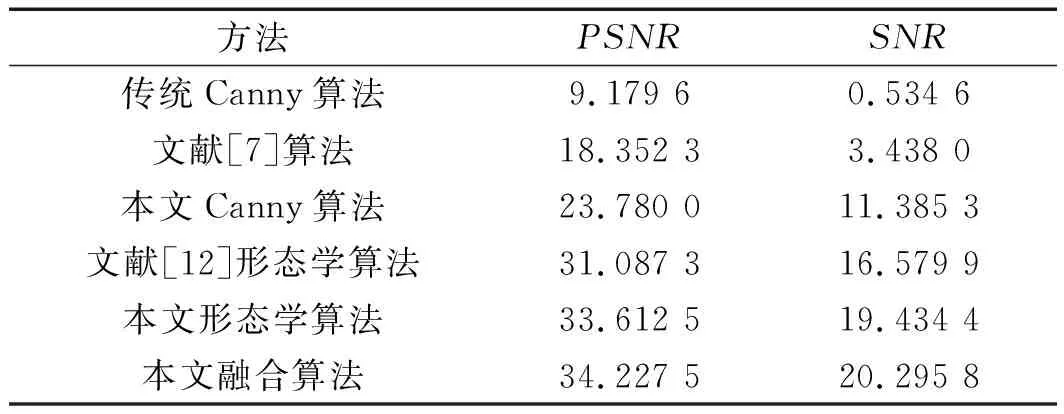
表1 边缘检测算法PSNR、SNR值

从图1和表1中可以看出：

(1)本文新型形态学采取多尺度多结构的结构元素，利用结构元素尺度小去噪能力弱，但能保护图像的细节信息，结构元素尺度大去噪能力强，但会使图像细节模糊的特点，使用3个不同尺度的结构元素进行形态学操作，并且公式(13)可以通过因子i的取值控制结构元素尺度来控制去噪效果。因此能够达到在保护图像细节的同时，取得良好的去噪效果；

(2)本文算法客观评价指标峰值信噪比(PSNR)和信噪比(SNR)均高于其他算法，并且计算复杂度较小。

对Lean图加入不同噪声浓度的椒盐噪声结果如表2所示。

表2 不同噪声浓度下PSNR、SNR值

从表2中可以看出：随着椒盐噪声浓度的增加，本文形态学依然具有良好的去噪效果。

加入5%浓度噪声的齿轮图像实验结果如图2所示。

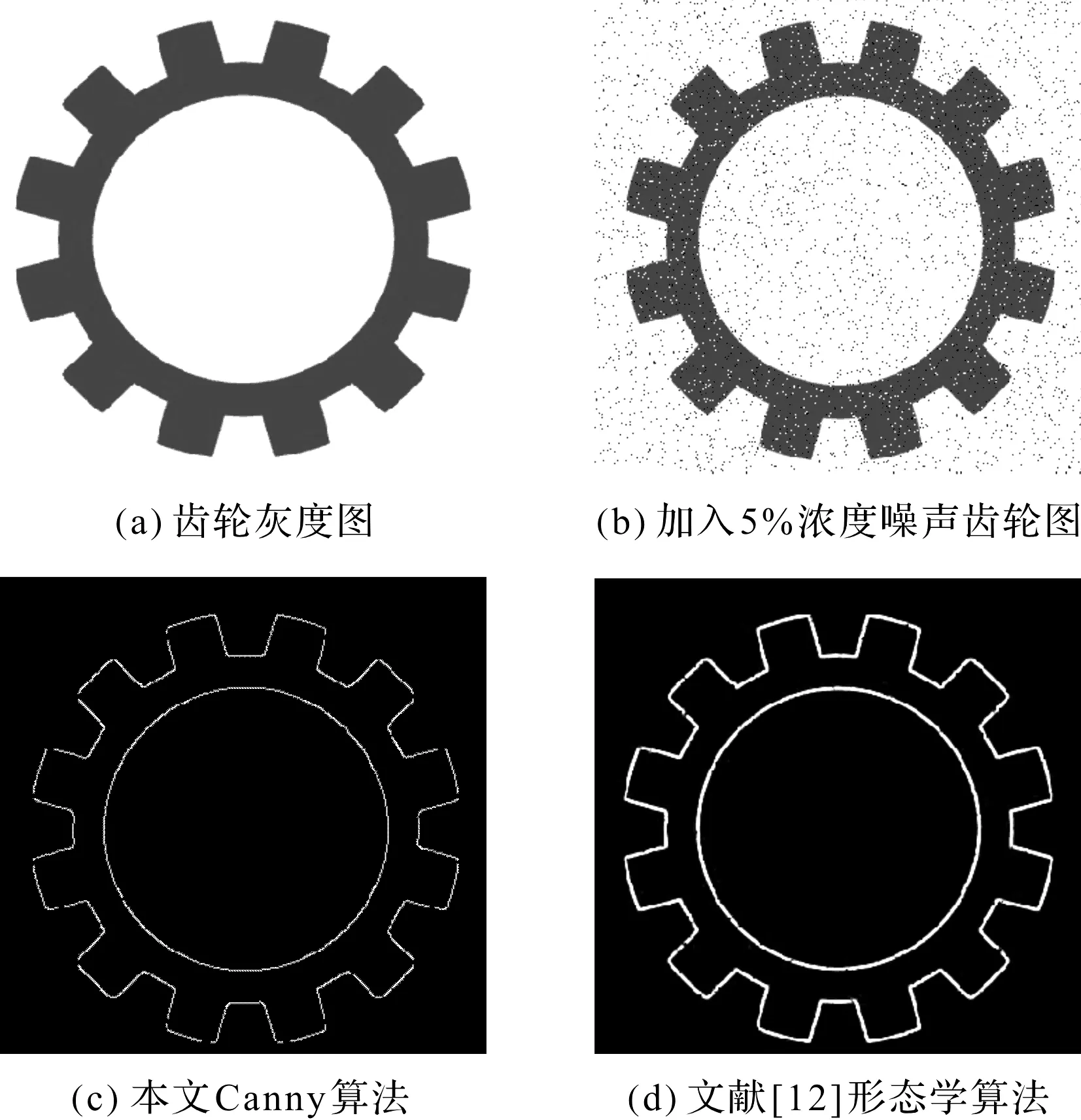
图2 实验2

加入5%浓度的噪声齿轮图像评价指标如表3所示。

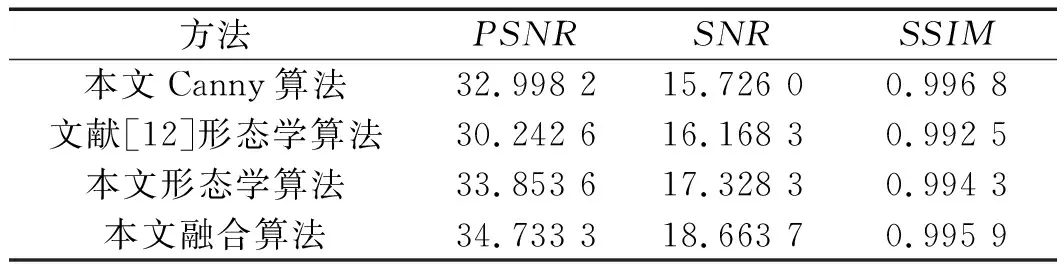
表3 边缘检测算法PSNR、SNR和SSIM值

从图2和表3中可以看出：当加入5%的椒盐噪声检测齿轮图像时，本文自适应融合算法得到的齿轮边缘图像边缘连续、轮廓清晰，并且客观评价指标均高于其他算法。

加入方差0.007高斯白噪声，检测复杂齿轮图像结果如图3所示。

图3 实验3

5 结束语

针对含噪齿轮图像边缘检测过程中存在难以有效抑制噪声和检测更多真实边缘等问题，本文提出一种融合改进的Canny算子和新型数学形态学算法，结合小波分解的优势，使其在图像噪声浓度较高时依然具有良好的去噪效果和检测效果。

实验及研究结果表明：算法自适应加权融合更好地结合了单独使用Canny算子和数学形态学的优势，使得最终边缘检测图在去噪效果、边缘检测数量、边缘连续清晰效果和定位精度方面都有明显的提高；并且本文新型形态学算法计算复杂度更小，具有良好的自适应性。根据以上叙述，本文算法具有良好的去噪效果和边缘检测效果，计算复杂度低，并且同样可用于其他图像，是一种可行的无监督算法。

本文算法也存在一定的不足，融合后的边缘图像部分真实边缘未能完全检测出来；算法用于其他复杂图像时，能否依然能保持良好的检测效果，这是将来需要研究的问题。