基于F-矩阵的高维协方差矩阵相等性检验

李顺勇，王一静，张晓琴

（1.山西大学 数学科学学院，山西太原030006；2.山西财经大学统计学院，山西太原030006）

一、引言

在生物学、神经科学以及刑事技术和物证检验中[1，2]，经常涉及到多元回归分析中的多元随机向量及其相关统计分析。当考虑多个多元分布的总体时，各个总体的协方差矩阵之间是否相等是进行统计推断的一个必要环节，因为许多多元统计分析方法都需要协方差矩阵相等这一前提，即要满足多个总体协方差矩阵的齐次性。由此可见，对协方差矩阵的齐次性进行检验是一个重要的研究课题。

考虑两个 p 维独立总体 X=（ξ1，ξ2，…，ξp）′和 Y=（η1，η2，…，ηp）′，其均值向量和协方差矩阵满足：

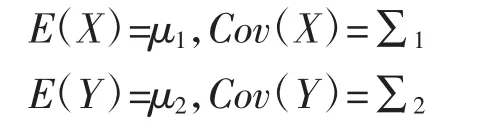
假设 ξ1，ξ2，…，ξn1是来自总体 X 的样本，ξj=（ξ1j，ξ2j，…，ξpj）′，j=1，2，…，n1。η1，η2，…，ηn2是来自总体Y的样本，ηk=（η1k，η2k，…，ηpk）′，k=1，2，…，n2。本文考虑两个总体协方差矩阵相等性检验问题，即如下的假设检验问题：

目前关于双样本协方差矩阵的相等性检验已经有许多研究成果。John S（1971）[3]和 Hisao N（1973）[4]讨论了维数p固定时经典假设（即p＜n）和针对正态总体的检验方法，但这类方法在高维数据情形下会失效。Bai等（2009）[5]和 Jiang等（2012）[6]在维数 p 和样本量n成比例増长的假设下，都运用大维随机矩阵理论并在似然化检验的基础上提出了关于大维协方差矩阵的相关检验方法。Chen等（2010）[7]在所用检验统计量有渐进框架的限定下，给出了当维数和样本量同时趋于无穷大时的检验方法。之后，对于高维数据，Xu（2014）[8]提出了一种伪似然比检验方法来检验两个大维总体协方差矩阵的比例性及相等性，但检验结果仅适用于比例参数。Jiang（2016）[9]基于Rao得分检验，在大维架构下提出了适用于高维情形下非正态分布的修正得分检验方法。何冰等人（2019）[10]根据 Jiang（2016）[9]统计量的形式提出了一个新的检验统计量，并引用Zheng（2012）[11]在2012年给出的高维F-矩阵的线性谱统计量中心极限定理，证明了检验统计量的渐进性，但对于维数相对于样本量较大的情况，何冰等人（2019）[10]提出的方法效果并不理想。

针对以上的相关研究成果，本文借鉴Jiang（2016）[9]提出的修正 Rao得分检验，针对 Xu（2014）[8]提出的检验方法中比例参数的限制问题给出解决方案，主要思想是对其极限分布进行研究。

二、基本知识

这一部分简要介绍与F-矩阵相关的基本概念以及定理。

定义1[8]：（经验谱分布与线性谱统计量）对任意具有实特征根i=1，2，…，p）的 p 阶方阵 M，其矩阵M的经验谱分布（Empirical spectrum distribution，ESD）可以定义为一个一维的分布函数：

其中，（I·）代表示性函数，RR表示实数集合。

定义2[11]：（F-矩阵）考虑两个p维独立总体，X=（ξ1，ξ2，…，ξp）′，Y=（η1，η2，…，ηp）′，其均值向量和协方差矩阵分别为：

设ξj=（ξ1j，ξ2j，…，ξpj）′，j=1，2，…，n1，ηk=（η1k，η2k，…，ηpk）′，k=1，2，…，n2，分别为来自总体 X 和 Y 的样本，则两者的样本协方差矩阵分别为：

其中 n2＞p。

为研究F-矩阵的线性谱统计量的中心极限定理，本文给出了两个假设[9]。

（1）对于任意固定的 ε0＞0，有：

其中，I（·）为示性函数。

Fc1，c2所对应的支撑集是复平面上一个包含区间［a′=（（1-）（/1+））2，b′=（（1+）（/1-））2］的开集合，定义A为一族函数的集合，且A=｛g1，g2…｝。函数 g1，g2，…均在包含区间［a′，b′］的开区域上解析。在A上定义经验过程Gn:=｛G（ng）｝。

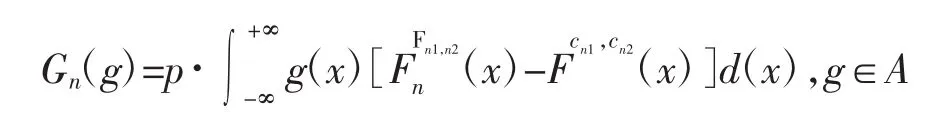
这里Fcn1，cn2（x）是把（2）式中参数c1、c2换成cn1、cn2的极限分布。

下面介绍 Zheng（2012）[11]提出的 F-矩阵的线性谱统计量的中心极限定理（Central limit theorem，CLT）。

定理1[11]：在定义2的记号下，如果假设（1）和（2）成立，则对于所有的 j、k，有：

其中，βx和βy是与四阶矩相关的常数，τ满足以下条件：

其中，r→1+表示r从右趋于1。

三、新检验统计量及其渐进性

（一）TX[8]和 TJ[9]

关于高维双样本协方差矩阵的相等性检验，Xu等[8]在2014年提出了伪似然比检验TX，如下所示：

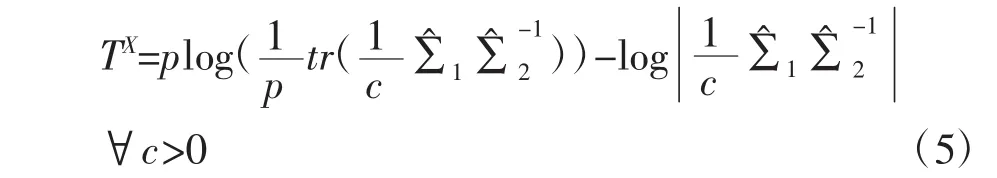
TX是针对两个总体协方差矩阵的比例性检验，但对于协方差矩阵相等性检验来说，比例参数c的存在会降低检验性能。具体来说，在协方差矩阵相等性检验中，TX首先需要一些样本来消除比例参数c的影响，再进行检验，这样就使得检验效果受到影响。

针对协方差矩阵相等性检验问题，Jiang（2016）[9]对经典的协方差矩阵的得分检验进行修正得到了修正Rao得分检验，具体如下：

假设用区域生态模式中有m个实例，每个实例具有n个影响因子，将各个影响因子归一化处理，根据相关公式计算出关联函数值如式（2），标准差如式（3），再进行和积计算：

其中，修正Rao得分检验运用的大维样本协方差矩阵的线性谱统计量的中心极限定理是在更宽泛条件（当 p，n1→+∞ 时，cn1=p/n1→c1∈（0，+∞））下的中心极限定理，这就使得修正得分检验可以更广泛地应用，并得到了很好的检验效果。

（二）新检验统计量TNew

本文在随机矩阵理论下，对Xu等（2014）[8]提出的TX中的第一部分，借鉴Jiang（2016）[9]提出的修正Rao得分检验，并去除TX中的比例参数c，以此对Xu[8]等提出的伪似然比检验TX进行改进。检验∑1=∑2等价于检验∑1Ip，这使我们借用一个总体协方差矩阵的球度检验的思想，构造出以下检验统计量：

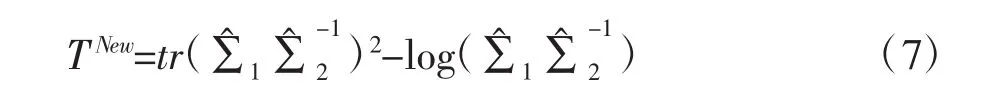
为了便于陈述，设两个p维独立总体X和Y满足以上条件：

E（X）=μ1，Cov（X）=∑1

记 x1，x2，…，xn1为来自于 X 的样本，y1，y2，…，yn2为来自于Y的样本。下面通过一个定理给出TNew的渐进分布。

定理 2：如果假设（1）、（2）及定理 1 的条件均成立，令：

则在原假设H0：∑1=∑2下，当n→∞时，检验统计量TNew有以下结论：

证明：根据线性谱统计量的定义对检验统计量TNew进行变形得到：

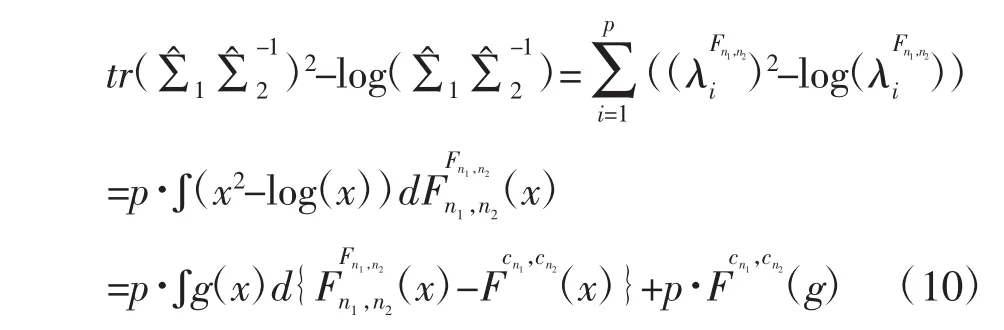
令g（x）=g1（x）-g2（x），且g1（x）=x2，g2（x）=log（x）。下面就g1（x）和g2（x）分别展开证明。

另外，经简化后，g1（x）的均值如下：

则g1（x）的均值可以分成三个部分。

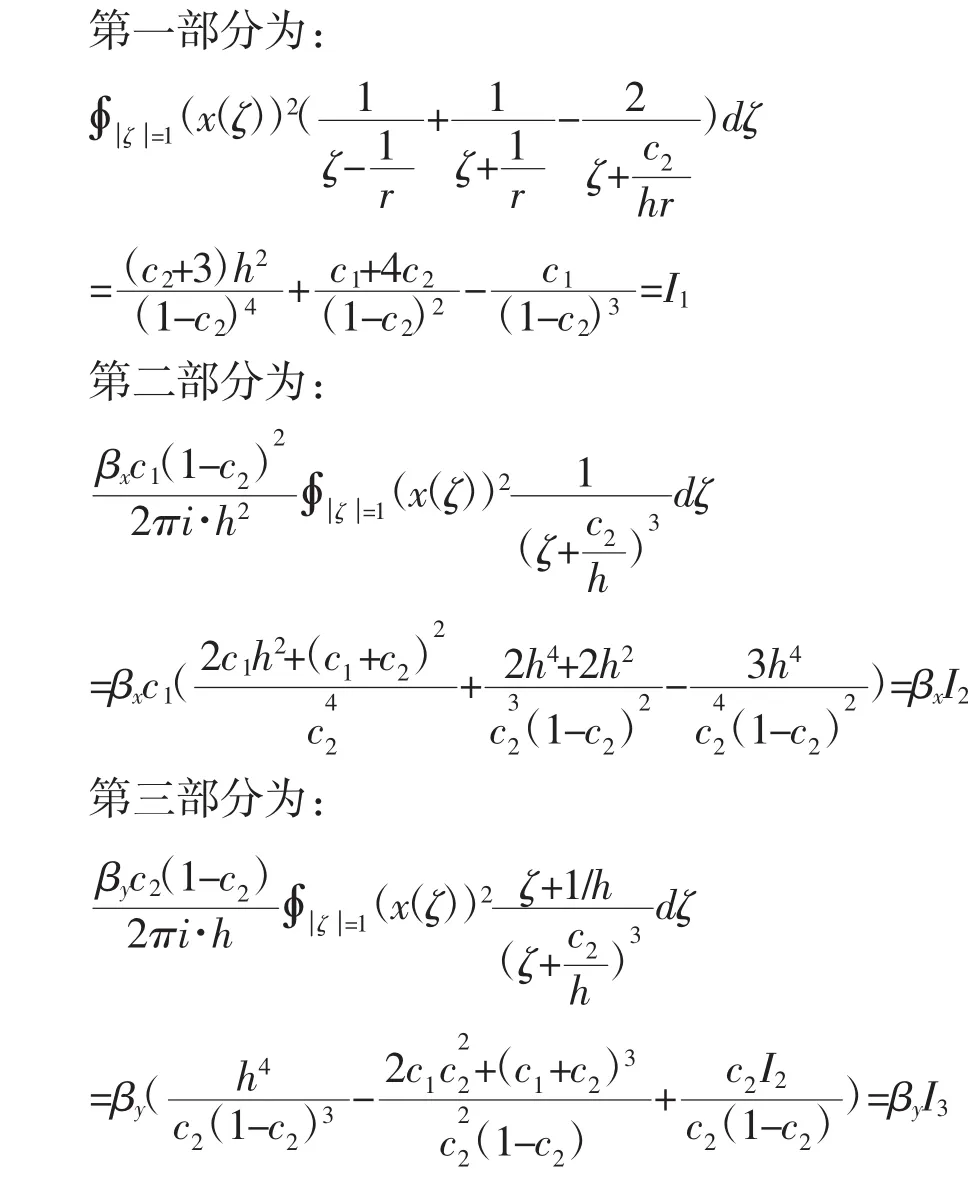
综合以上三个部分可得：μ（g2）=I1+βxI2+βyI3。

综合（1）、（2）可得：

以上完成了均值的证明，接下来进行协方差阵的证明。由定理1可知，其协方差cov（g）同样也可分成三部分。

第一部分为：

综合三部分可得：

即式（8）成立，进而有：

即式（9）成立，证毕。

四、模拟实验

本节通过模拟试验对检验统计量TNew的表现进行评估，主要对高维多元正态分布和非正态分布下TNew和TX两个统计量的检验水平ˆ和检验功效ˆ进行了仿真研究与比较。本文用到的评价标准有两个，

其中，tH0表示统计量在原假设下模拟数据中的值，z1-α表示标准正态分布的上侧α分位数，#表示tH0≥z1-α的总次数。在我们的试验中，选择m=1 000且选择显著性水平α=0.05。

（2）经验功效βˆ。本文采用的另一个评价指标是经验功效βˆ。在备择假设下进行模拟，定义经验功效βˆ 为：

其中，tH1表示统计量在备择假设下模拟数据中的值，# 表示 tH≥的总次数。特别地，是经验功效的评判点，是对原假设下进行的m次试验结果中第mα大的点。

此外，在模拟实验中对参数进行了设置。其一，两个总体协方差矩阵分别为∑=和∑12，其中参数＞0，ρ∈（-1，1）。其二，分别设置ρ=0或0.5，=1。当ρ=0时，∑1=∑2=Ip用于计算检验水平；当 ρ=0.5 时，∑=I，∑=（0.51p2即∑1Ip，则可以用于检验功效的计算。其三，维度 p 分别取 80、160、320、640，相应地取 p/n1、p/n2=0.2、0.5、0.8。

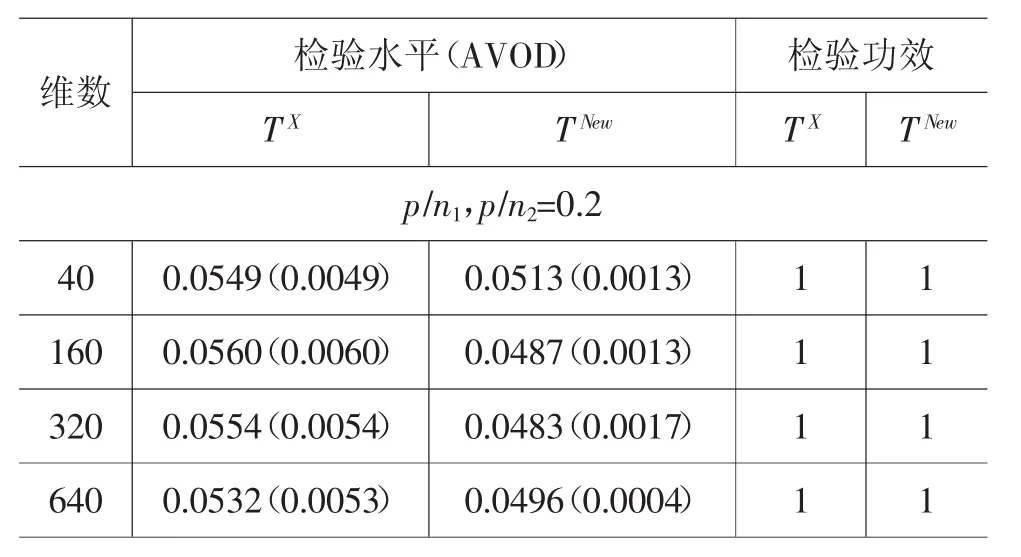
表1 正态分布下TX和TNew的检验水平（AVOD）和检验功效（百分比）

（续表1）

（1）对于正态分布，样本 ξ1，ξ2，…，ξn1取自正态总体N（p0，∑1），样本 η1，η2，…，ηn2取自正态总体N（p0，∑2）。

（2）对于 Gamma分布，样本 ξj=Wj，其中对于 每 一 个 j=1，2， … ，n1，Wj独 立 同 分 布 于 Ga（2.5，0.5）；样本 ηk=，其中对于每一个 k=1，2，…，η2，zk独立同分布于 Ga（2.5，0.5）。

表1和表2从检验水平和检验功效两个方面对TNew和TX进行了比较，其中TX是Xu等[14]在2014年提出的伪似然比检验（5），这里取c=1。

从表1可以看出，在正态分布下，TNew和TX都有相似的检验水平趋势。从检验水平和标准水平差的绝对值来看，TNew更接近于5%的标准水平。此外，从检验功效这个方面，因为TX是针对任何未知的比例常数c提出的，所以很明显，当c=1时，TNew比TX具有更大的能力。这是因为，TX首先必须牺牲一些样本来取消未知的c，然后使用剩余的样本来检验。总的来说，TNew比TX表现更佳、更稳健。

表2 Gamma分布下TX和TNew的检验水平（AVOD）和检验功效（百分比）

从表2可以看出，在Gamma分布（非正态分布）下，不论从检验水平还是检验功效来看，TNew的总体性能比TX更好，这为高维数据下的协方差矩阵相等性检验提供了一个更好的选择。

五、结论

文章针对高维数据双样本协方差矩阵的相等性问题，提出了一种新的检验方法，并基于随机矩阵理论证明了其渐近正态性。新的检验统计量结合Jiang（2016）[9]的想法，弥补了 Xu（2014）[8]检验方法中的不足。模拟实验结果表明，TNew在检验两个高维总体协方差矩阵相等性时更具有稳健性，并且对高维正态分布和非正态分布都有很好的效果。